Расчет зеркальной антенны с рефлектором в виде параболического цилиндра

Анализ любой зеркальной антенны сводится к решению задачи дифракции электромагнитной (ЭМ) волны, возбуждаемой облучателем, на рефлекторе (зеркале). Как известно, существует три основных метода решения подобных задач: метод геометрической оптики, метод физической оптики и метод интегральных уравнений [1-3].

Метод геометрической оптики заимствован из классической теории света. В его основе лежит закон Снеллиуса и принцип Ферма. Он применим лишь для зеркал сверхбольших электрических размеров. Данный метод использован в [4] для анализа зеркальной антенны с диаграммой направленности специальной формы. В [5] этим же методом исследовано поле излучения параболической антенны в случае ее возбуждения импульсным ЭМ полем. В [6] даже рассчитано поле в ближней зоне антенны таким методом, что в корне неверно. Поле, отраженное зеркалом, в ближней зоне имеет все шесть компонент (три компоненты вектора Е и три компоненты вектора Н ), даже если оно облучается поляризованной волной, а метод геометрической оптики не учитывает векторный характер поля, поэтому для его анализа в ближней зоне он неприменим, его можно использовать лишь для дальней зоны, где поле является чисто поперечным.

Метод физической оптики состоит в определении ЭМ поля излучения по известному рас- пределению возбуждающего поля на плоской поверхности раскрыва зеркала (апертуре) в соответствии с теоремой эквивалентности. Пренебрегая влиянием ряда факторов, считают, что излучающей поверхностью является только апертура. Для упрощения задачи излучением относительно малых электрических поверхностных токов на теневой стороне зеркала пренебрегают. Данный подход имеет очень много ограничений. Он неприменим для рефлекторов с малыми электрическими размерами, а также в том случае, если локальный радиус кривизны рефлектора не везде достаточно велик по сравнению с длиной волны. Вдобавок ко всему этот метод не учитывает краевые эффекты на кромках зеркала. Еще одним ограничением является то, что этот метод не учитывает многократного рассеяния, то есть он не учитывает обратное воздействие зеркала на рефлектор, и им невозможно рассчитать дифракцию на нескольких телах. Данный подход дает неудовлетворительные результаты, если рефлектор относится к группе самозатеняющихся [1]. А самое главное – им невозможно корректно рассчитать ЭМ поле в ближней зоне антенны. Но все же метод физической оптики точнее метода геометрической оптики. Применение этого метода к расчету эффективной площади рассеяния зеркальных антенн описано в [7].

Большинства вышеописанных недостатков лишен метод интегральных уравнений. Только этот метод может дать точное решение задачи дифракции. Он заключается в определении поля, рассеянного зеркалом, по наведенным на нем токам. Функции распределения токов на поверхности зеркала определяются из решения интегрального уравнения. Другими словами, из решения краевой задачи на поверхности зеркала с учетом граничных условий. Этот метод намного сложнее методов физической и геометрической оптики. Самой большой трудностью при решении интегрального уравнения является наличие сингулярности в его ядре. Этому методу в литературе уделяется очень мало внимания, по-ви-димому, из-за его сложности. Второй причиной (в литературе она практически не обсуждается) является следующее обстоятельство. Обычно при расчете любой антенны (в том числе и зеркальной) анализируется поле в ее дальней зоне и, как правило, не обращается внимание на то, что традиционные методы не применимы для анализа ЭМ поля в ближней зоне антенны (любой) [8]. Более того, отсутствует предельный переход ЭМ поля к поверхностному электрическому току Л на антенне, так как из электродинамики известно, что функция Г| связана с напряженностью магнитного поля H соотношением П = [й0,я], где «о – вектор нормали к поверхности, на которой ищется функция Л . Задача определения поверхностной плотности тока л на антенне (любой) является некорректной [8], поэтому небольшие ошибки в л могут привести к огромным (в литературе даже есть термин «катастрофическим») ошибкам для ЭМ поля. Поэтому необходима регуляризация при определении л •

В работе [9] предпринята попытка корректно подойти к численному решению задачи дифракции на незамкнутых поверхностях произвольной формы. Однако эта работа имеет ряд недостатков. Во-первых, она содержит ряд опечаток, например, в выражении для коэффициентов Ламе в (5). Во-вторых, неизвестными функциями в системе сингулярных интегральных уравнений (СИУ) (6) являются проекции плотности тока на единичные орты криволинейной системы координат не в точке источника, как это должно быть, а в точке наблюдения, как будет показано ниже, в криволинейных системах координат они, в отличие от декартовой, не равны друг другу, причем эти функции в [9] являются функциями только координат точки источника, а это неверно, так как проекции вектора плотности тока, протекающего в точке источника, на единичные орты в точке наблюдения должны быть функциями координат как точек источника, так и точек наблюдения. Другими словами, в [9] вообще непонятно, что выступает в качестве неизвестных функций в системе СИУ. Численный алгоритм решения системы СИУ является не чем иным, как методом дискретных вихрей [10-11]. Данный алгоритм в виде [9], даже при его реализации на современных ЭВМ, позволяет рассчитывать распределения токов на зеркалах только электрически малых размеров (размер апертуры которых не более 2Хх 2Х), естественно, при условии корректно составленной системы СИУ.

В данной статье описан метод, позволяющий корректно составить систему СИУ относительно неизвестных составляющих плотности тока на поверхности параболического цилиндра, возбуждаемого облучателем. Предложен численный алгоритм решения этой системы, позволяющий рассчитывать распределения токов на зеркалах как малых, так и весьма больших электрических размеров.

Постановка задачи. Система гиперсингулярных интегральных уравнений

При расчете будем использовать следующую физическую модель антенны. Рефлектор представляет собой бесконечно тонкий идеально проводящий параболический цилиндр с фокусом f (см. рис. 1). Его раскрыв (апертура) имеет конечные размеры laxlb. Рефлектор возбуждается облучателем. В качестве облучателя используется полосковый вибратор, представляющий собой бесконечно тонкую идеально проводящую полоску длиной 2 l и шириной 2 w , возбуждаемую в области зазора шириной 2А сторонней гармонической ЭДС. Полосковый проводник предполагается достаточно узким (2w, X),так что поперечной составляющей поверхностной плотности электрического тока ^Y пренебрегаем по сравнению с продольной //* . Волна, возбужденная вибратором, падает на рефлектор и наводит на нем поверхностный ток, возбуждающий волну, которую будем называть отраженной. Волна, отраженная от зеркала, падая на облучатель, в свою очередь, наводит на нем дополнительные токи.

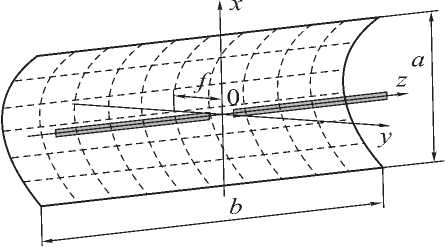
Рис. 1. Зеркальная антенна с рефлектором в виде параболического цилиндра

Запишем выражение, связывающее вектор напряженности электрического поля Е в данной точке пространства с векторным электродинамическим потенциалом А в этой точке [12]:

1соее₀Е = к"А + graddiv^ , (1)

где со – циклическая частота; Е_о – электрическая постоянная; к = 2л/^ – волновое число; л – длина волны; А – векторный электродинамический потенциал равный

Ti= jfj^G^p^oS,         (2)

s

G^P^ "" функция Грина; p , q – координаты точки наблюдения и точки источника соответственно; S – излучающая поверхность.

Известно следующее соотношение [13]: div^f)^)^/^)^

(grad^ G^p,q),T\^ + G(p,q)dw_p fj(₉) .

Индекс p в операторах div и grad означает, что дифференцирование производится по координатам точек наблюдения. Так как div^ fj(^) = 0 , то в рассматриваемом случае div^(rj(?)G(A?)) = (gradpG(;?,^),fi(^)). (3)

н-grad^, [grad^ G(/2,^),fj(^)^6/S.

Для упрощения анализа такой антенны удобно использовать систему координат параболического цилиндра a , p, z [13]. Связь криволинейных координат с декартовыми определяется формулами

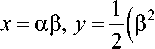
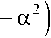
z = z.

точки наблюдения без штрихов p(a,p,zp ^_qp – элементы матрицы ортогонального поворота (^ = a,P,z; q = a'$A, определяемые выражениями

„ Ilf &' dx 9V dv 9z' dz)

^>an= ----+ ---- +--b (6)

4 p hq hp ( 8q dp dq dp dq dp )

где h_q И h_p – коэффициенты Ламе, равные [13]

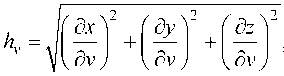
v = q,p.

Излучающая поверхность S (рефлектор) совпадает с частью координатной поверхности a = V2/, ограниченной по координате P отрезком \-al4if,al45j^ а по координате z отрезком [-6,6] . Плотность полного тока, наведенного на поверхности S (то есть сумма плотностей токов, наведенных на обеих ее сторонах), будет иметь лишь две составляющие (касательные к поверхности S ) - Пр- и n? С учетом сказанного выше и выражений (2) и (5), можно от векторного выражения (4) перейти к системе скалярных соотношений:

Tv ь itose0EP = J jp2 (Пр-^р-р + чА-'р)G + a -b

1 d ( 1 dG, x A A l^r|P'^'«) ⁺ h_p dp ' h^ du.

При переходе к скалярным выражениям необходимо учесть тот факт, что проекции вектора П на единичные орты 4, 4, 4 в точке источника q и проекции вектора П на единичные орты G ’ ^ ’ *z в точке наблюдения p связаны друг с другом через матрицу ортогонального поворота:

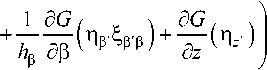
hpd^>'dz',

где p = a,^,z,

Па(Л9) dpt/V/) ApA

ААР’Ч) Цм) MN WN ^A?^ ^A?^

^zAp^}

ЪМ

^ApA

пАч^ Пр^ пАч\

Здесь и далее координаты точки источника будем обозначать со штрихами q^a'^’²'), а координаты

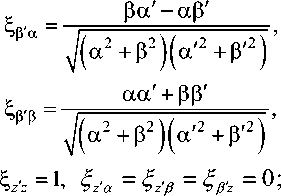
G(a,p,z,p',z'j = ехр[-/А7?]Д4л/?) - функция

Грина свободного пространства;

R = ^(aP-a'P')‘ + +0.25^р²-Р'²-a²+a'²) +(z-z'^A^

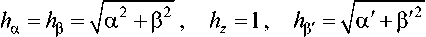
коэффициенты Ламе; a' = V2? – - координата зеркала. Выражения (7) справедливы для любой точки пространства, в том числе и для ближней зоны. При R^O подынтегральные выражения в (7) обращаются в бесконечность.

Чтобы вычислять поля в точке R = 0 и ее окрестности, представим выражения (7) в следую- щем виде:

напряженности электрического поля отраженной волн:

£ = Е™Д+£ОТР или в проекциях

E = Е™д*Ет\ p p       p ’

£0Tp определяется (8), а £™д соответствует полю ЭМ волны, возбужденной вибратором, и определяется выражениями:

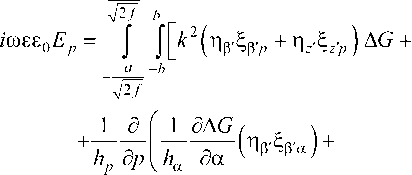
h^d^'dz' +

/Юе£оЕ7д= ff(^G1 +

i aG,л hp dpdz

vyv^dx'dy',

(H)

1 SAG / e и. ар Ь’^'Р

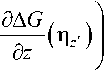
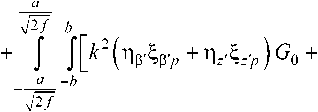
где e-ikRv

Gx =------,

4ttR,

7?, =^ap -x'^f ^0,25V' - a²)² +(z-z')².

i а м ac0

h_p cp\h_u da

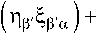
При выводе (11) было учтено, что координаты точки наблюдения являются координатами параболического цилиндра, а координаты точки источника – декартовыми. На поверхности зеркала

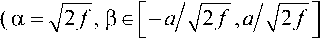
z g [-/>,a])

должны выполняться граничные условия для тангенциальных компонент напряженности электрического поля:

^ = 7Г™^Д + Е°^тр = 0, t = P,z, (12)

Функция Gq является произведением разложения функции cxp(-/A7?) в ряд Тейлора в окрестности точки R =0 на R , то есть описывает асимптотическое поведение функции Грина G при R^O , поэтому ядра, содержащие EG и производные от нее до второго порядка включительно (так как взяты первые три члена ряда Тейлора) не имеют особенностей при R = Q и являются регулярными, а ядра, содержащие G_o и производные от нее, являются сингулярными и гиперсингулярными. Выделение особенностей из ядер в таком виде позволяет построить квадратурные суммы метода дискретных вихрей [10-11] для вычисления сингулярных и гиперсингулярных интегралов.

Напряженность электрического поля E в точке наблюдения p будет складываться из напряженности электрического поля падающей £-пад и

Подставляя (8) и (11) в (12), получаем два гиперсингулярных интегральных уравнения (ГСИУ) относительно неизвестных функций распределения компонент плотности тока на поверхности зеркала n₽', n? и на поверхности облуча-обл .            1

теля Пу :

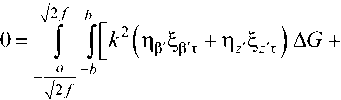
(Пр'^Уа

lM 1 aAG hT dz[^ha da i aAG

^^r

(пр’^'3

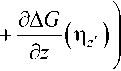
h^d^'dz' +

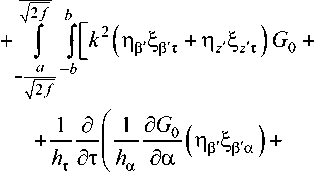
теля, то поле, отраженное от зеркала, на поверхности вибратора можно определить с помощью выражений (7) (без выделения особенности), учитывая при этом, что координаты точки наблюдения должны быть декартовы:

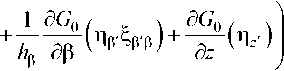
h^d$ dz' +

Z0)880£™3

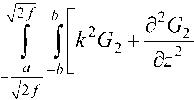
x\„,h^d^>dz' +

+ J J k^.j, G^-~jr чТ^'- (13) ^J             h otoz

Теперь рассмотрим поверхность облучателя. Для определения координат точек наблюдения бу-

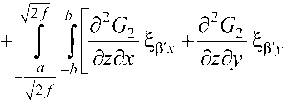
r\p h^d^'dz', (16)

дем использовать декартову систему координат, так как облучатель – полосковый вибратор. На его поверхности также должно выполняться граничное условие для тангенциальной компоненты напряженности электрического поля E_ = 0 . В данном случае напряженность поля на его поверхности будет складываться из напряженности электрического поля отраженной от вибратора волны ЕУ^ , напряженности электрического поля отраженной от зеркала волны (в данном случае будем называть ее падающей на облучатель Е™^д ) и стороннего поля, приложенного к зазору вибратора £5 :

£"'p + £™л + ££= 0.

Сначала запишем выражение для поля волны, отраженной от вибратора.

где %p-_v и ^p-_r - проекции орта у на орты i_x и i_v, равные

_ 1 Sx' _       ot'

_ 1 ay _     P'

A₽’< V« +p'2 ’

G2=i^’ Л2=[(Х-а0₽')2 +

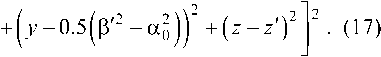
Подставляя (15) и (16) в (14), получаем еще одно ГСИУ:

нв88₀£°^тр - j |[а²АС^о6л +

-Z(O880£^T

52А£о6л

vx^dx'dz' +

a -b _

£7

a2G2 dz2

т|_, h^d^>'dz' +

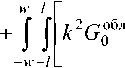
8z2

^Q обл _ ^обл _ ^-обл

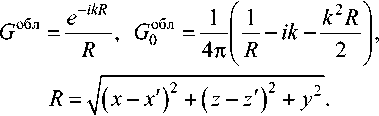
| dzdx ^{13 л} SzSy

^p-v Пр,Ар^Р'(£' +

обл , 52АОобл

dz обл . S G,

p °®^л dxdz +

о

dz2

nTdx'dz'. (18)

При выводе выражения (15) также учтено, что отраженное поле можно было бы считать в ближней зоне, и в том числе на поверхности вибратора. Теперь запишем выражение для поля волны, отраженной от зеркала. Так как в данном случае мы рассматриваем поле на поверхности облуча-

Итак, уравнения (13) и (18) совместно представляют собой полную систему ГСИУ относительно неизвестных функций распределения компонент плотности тока на поверхности зеркала Пр-, nz- и на поверхности облучателя ^обл . Напряженность стороннего электрического поля в случае симметричного запитывания обоих плеч удобно представить в виде:

E^CT^ = .^Eo V^1-(^z/^A)²’ ²^\-1Дх& [-w, w];

0,z £ [-/,/], x t [-w,w].

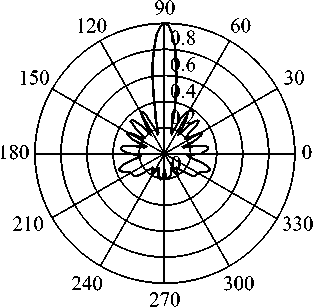
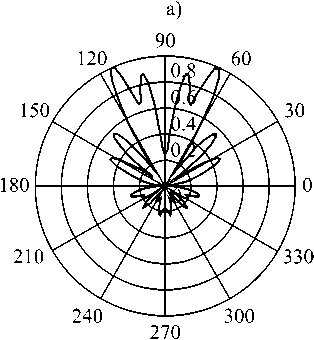
Рис. 2. Диаграмма направленности зеркальной антенны с рефлектором в виде параболического цилиндра: а) г(110°,ф),б) F(0,90°)

Полученная система решалась методом коллокаций, в качестве точек коллокации были использованы гауссовы узлы (нули полиномов Лежандра). Чтобы учесть особенность поведения тока на кромках зеркала и кромках вибратора, будем считать, что неизвестные составляющие функции распределения плотности тока на поверхности рефлектора и облучателя можно представить в виде рядов по полиномам Чебышева первого

) и второго (^m ) рода с весовыми функциями, причем эти ряды сходятся в среднем:

nP'(PV) =

= Z Z С ^Ц^ГИU_m ^J2f/a) X 777=0 /7 = 0

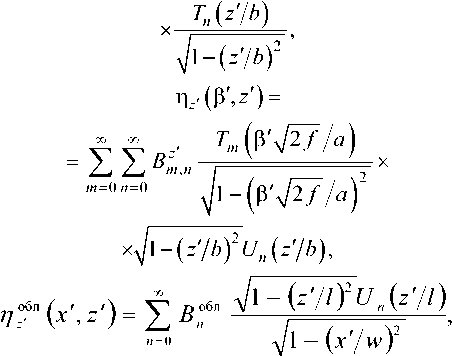
где ®m,n – неизвестные коэффициенты разложения функций T|p(PV) и n^(P\^') соответственно; s°^6jl – неизвестные коэффициенты разложения функции n?(V,z'). Гиперсингулярные интегралы вычислялись методом дискретных вихрей [10-11].

На рис. 2 представлены диаграммы направленности антенны с фокусом / = зя и апертурой 5Ях52, возбуждаемой вибратором длиной O?5/^/ и шириной 0,052 , расположенным в фокусе зеркала (а – в вертикальной плоскости 0 = 110 , б – в горизонтальной плоскости ср = 90 ). Диаграмма направленности излучающей системы определялась следующим образом [15]:

F(0,cp)

max||F(9,cp)||

где

E (0, q>) = ^(O^j + E^O^),

^(^ф), ^(^ф) -компоненты вектора напряженности электрического поля Е(0,ф) в дальней зоне (сферическая система координат).

Как видно из рис. 2, основная часть энергии падающей волны отражается от зеркала, причем чем больше апертура, тем большая ее часть отражается, однако так как зеркало имеет конечные размеры, то часть ее проходит за него. В вертикальной плоскости происходит фокусировка луча. Предложенную методику несложно обобщить на зеркала более сложной формы (параболоид, гиперболоид и т.д.). Результаты расчетов совпали с результатами численного моделирования в системе CST Microwave Studio. Описанный выше численный алгоритм решения системы двумерных ГСИУ обладает более быстрой сходимостью и большей вычислительной устойчивостью по сравнению с известным методом дискретных вихревых рамок [10-11], что позволяет реализо- вывать его на компьютерах с относительно малой оперативной памятью.

• 1.    Вуд П. Анализ и проектирование зеркальных антенн. Пер. с англ. под ред. О.П. Фролова. М.: Радио и связь, 1984. – 208 с.

• 2.    Фрадин А.З. Антенно-фидерные устройства. М.: Связь, 1974. –440 с.

• 3.    Айзенберг Г.З., Ямпольский В.Г., Терешин О.Н. Антенны УКВ. Под ред. Г.З. Айзенберга. Ч.1. М: Связь, 1977. – 384 с.

• 4.    Прохоров И.О., Кондратьева А.П. Зеркальная антенна с диаграммой направленности специальной формы // Антенны. Вып. 12(151), 2009. – С. 9-12.

• 5.    Скулкин С.П., Турчин В.И. Импульсное поле офсетной параболической антенны в дальней зоне // Антенны. Вып. 6 (145), 2009. — С. 3-7.

• 6.    Будагян И.Ф., Щучкин Г.Г. Характеристики поля зеркальной антенны с корректирующим импедансом в ближней и дальней зонах при работе со сверхкороткими импульсами // Антенны. Вып. 4 (131), 2008. – С. 20-26.

• 7.    Кирьянов О.Е., Мартынов Н.А. Комбинированная итерационная методика расчета эффективной площади рассеяния зеркальных антенн // Антенны. Вып. 10 (149), 2009. – С. 17-25.

• 8.    Неганов В.А. Физическая регуляризация некорректных задач электродинамики. М.: Сайнс-Пресс, 2008. – 450 с.

• 9.    Давыдов А.Г., Захаров Е.В., Пименов Ю.В. Метод численного решения задач дифракции электромагнитных волн на незамкнутых поверхностях произвольной формы // ДАН СССР. Т. 276. № 1, 1984. – С. 96-100.

• 10.    Лифанов И.К. Метод сингулярных интегральных уравнений и численный эксперимент. М.: Янус, 1995. – 520 с.

• 11.    Вайникко Г.М., Лифанов И.К., Полтавский Л.Н. Численные методы в гиперсингулярных интегральных уравнениях и их приложения. М.: Янус, 2001. – 508 c.

• 12.    Неганов В.А., Осипов О.В., Раевский С.Б., Яровой Г.П. Электродинамика и распространение радиоволн. Под ред. В.А. Неганова и С.Б. Раевского. Изд. 4. М.: Радиотехника, 2009. – 774 с.

• 13.    Анго А. Математика для электро- и радиоинженеров. Пер. с франц. под ред. К.С. Шифрина. М.: Наука, 1965. – 780 с.

• 14.    Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М-Л.: Энергия, 1967. – 376 с.

• 15.    Марков Г.Т., Сазонов Д.М. Антенны. М.: Энергия, 1975. – 528 с.

CALCULATION OF PARABOLIC CYLINDER REFLECTOR ANTENNA

Klyuev D.S.

Thecalculation ofparaboliccylinder reflector antenna by2D singular integral equation (2DSIE) method is represented in this paper. The system of 2DSIE for surface current density on the reflector and emitter calculation was reduced. The numerical algorithm of solving this system is represented. Radiation patterns of this antenna is represented.