Расчет звукоизоляции элементов двойного остекления систем шумозащиты на участке испытаний двигателей транспортных машин

Введение. Теоретическое исследование генерации шума при обкатке двигателей транспортных машин, разработка моделей шумообразования позволяют рассчитать уровни шума, возникающие в рабочей зоне операторов. Наиболее «слабым» элементом в ограждающих конструкциях является остекление и можно предположить, что именно оно излучает повышенные уровни шума. Само остекление имеет малый эффективный коэффициент потерь колебательной энергии. Применение вибродемпфирующих материалов в этом случае исключено. Для таких конструкций вибрационное поле определяется резонирующими формами собственных колебаний.

Современные технологии позволяют широко применять двойные и тройные стеклопакеты, которые обладают высокими характеристиками не только термоизоляции, но и шумоизоляции, по сравнению с однослойным остеклением. Предлагаемый расчет звукоизоляции таких многослойных элементов остекления позволяет подбором толщин стеклянных пластин и воздушных промежутков достичь санитарных норм шума на рабочем месте оператора.

Методы решения. Метод расчета звукоизоляции многослойных конструкций типа «сэндвич» существенно отличается от однослойных. Элементы ограждения следует выполнять многослойными, с различным количеством и механическими характеристиками слоев. Согласно данным работ [1-3] система уравнений для многослойной конструкции имеет вид:

^Р 1 ’ ( ^A1 + ^A 1 ' ) = ^P 2 ’ ( A 2 + ^A 2 ) ;

- a 1 A 1 + a 1 A ' = - a 2 A 2 + a 2 A ;

p ₂ [ A 2 exp ( - ia ₂ x 1 ) + A exp ( ia ₂ x 1 ) ] = p ₃ [ A 3 exp ( - ia 3 x 1 ) + A ' exp ( ia 3 x 1 ) ] ;

a ₂ [- A 2 exp ( - ia ₂ x 1 ) + A exp ( ia ₂ x 1 ) ] = a 3 [- A 3 exp ( - ia 3 x 1 ) + A ' exp ( ia 3 x 1 ) ] ;              (1)

P k - 1 [ ^Ak - 1 exp ( — ^iak - 1 ^xk - 2 ) ^{+ A}k - 1 exp ( ^iak - 1 ^xk - 2 ) ] = P k^Ak exp ( — ^iak^xk - 2 ) ;

a k - 1 [ ^{- A}k - 1 exp (^- ia k - 1 ^xk - 2 ) ^{+ A}k - 1 exp ( ia k - 1 ^xk - 2 ) ] = - a k A k exp (^{- ia}k^xk - 2 ) .

Из этой системы уравнений определяются коэффициенты отражения rp и проникновения tp волны давления r = A^ ;      t = Ak pk Ak           pk   Ak-1

Звукоизоляция определяется по формуле

ЗИ = 10lg-2, tp kA где tp =n tpt = у.

2         A 1

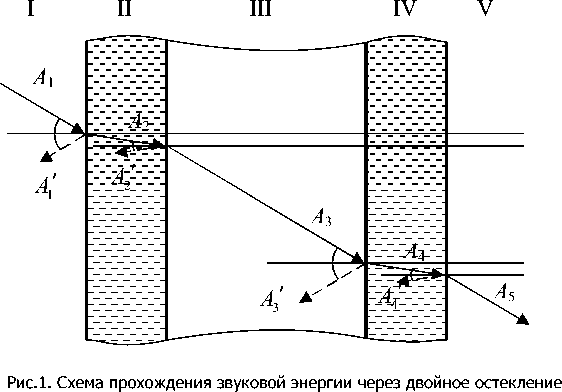
Поскольку двойное остекление имеет воздушный промежуток между стеклами, то количество границ между различными средами k =5 (рис.1). С точки зрения вычислений расчет коэффициента многослойной звукоизоляции сводится к следующей задаче: для каждой частоты f j из заданной последовательности (среднегеометрические полосы октавных или третьоктавных фильтров) найти

R=0- tp где tp – действительная часть комплексной величины tp.

Система уравнений для пяти сред будет выглядеть следующим образом:

P i ( ^A1 + ^A 1 ' ) = P 2 ( A 2 + A 2 ' ) ;

a 1 ( - A 1 + A 1 ) = a ₂ ( - A 2 + A ₂ ) ;

p ₂ ( A ₂ exp ( - ia ₂ x 1 ) + A ₂ ' exp ( ia ₂ x 1 ) ) = p ₃ ( A 3 exp ( - ia 3 x 1 ) + A 3 ' exp ( ia 3 x 1 ) ) ;

a ₂ ( - A 2 exp ( - ia ₂ x 1 ) + A 2' exp ( ia ₂ x 1 ) ) = a 3 ( - A 3 exp ( - ia 3 x 1 ) + A 3 ' exp ( ia 3 x 1 ) ) ;

p ₃ ( A 3 exp ( - ia 3 x ₂ ) + A 3 ' exp ( ia 3 x ₂ ) ) = p ₄ ( A 4 exp ( - ia 4 x ₂ ) + A 4 ' exp ( ia 4 x ₂ ) ) ;

a 3 ( - A 3 exp ( - ia 3 x ₂ ) + A 3 ' exp ( ia 3 x ₂ ) ) = a ₄ ( - A ₄ exp ( - ia ₄ x ₂ ) + A ₄ ' exp ( ia ₄ x ₂ ) ) ;

p ₄ ( A ₄ exp ( - ia ₄ x 3 ) + A ₄ ' exp ( ia ₄ x 3 ) ) = p ₅ A 5 exp ( - ia 5 x 3 ) ;

a ₄ ( - A ₄ exp ( - ia ₄ x 3 ) + A ₄ ' exp ( ia ₄ x 3 ) ) = - a 5 A 5 exp ( - ia 5 x 3 ) .

Здесь p k - плотности материала слоев системы; i - мнимая единица;

^ak =

^{2 Л} f j    А

-----cos 6 k , c_k

где 6 _k = arcsin h_k ;

- i| a|

где

a

2nfj ck-i

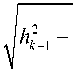
c Li c k ^{2 ,}

h k ^ i;

h k >  1,

c k – скорости распространения звука в материале слоев системы, причем:

c ₁ c ₂ c ₅

h 1 = h 2 = ... = h 5' где h k – толщина k - го слоя материала.

Угол падения звуковой волны на стекло со стороны источника шума является случайной величиной с равномерной плотностью распределения на участке 0 + 2 п . Поэтому 9 1 = arccos0,637 , а h 1 = sin 9 1 .

Двойное остекление представляет собой среду, состоящую из пяти компонент, в которой I, III и V среды являются воздушной составляющей, а II и IV – остекление. В системе (2) учтено, что в I – IV средах имеют место две волны: падающая (или пройденная) – A_k ; и отраженная –

A'. Пятая среда представляет собой воздушный объем производственного помещения, который имеет большие габаритные размеры. Поэтому в производственном помещении учитывается только пройденная волна. Тогда для двойного остекления система уравнений будет выглядеть следующим образом:

P i ( A i + A i ‘ ) = P 2 ( A + A 2 ‘ ) ;

a 1 ( - A 1 + A 1 ' ) = a ₂ ( — A 2 + A ₂ ' ) ;

p ₂ ( A ₂ exp ( - ia ₂ h 1 ) + A 2 ' exp ( ia ₂ h 1 ) ) = p 1 ( A ₃ exp ( - ia ₃ h 1 ) + A ₃ ' exp ( ia ₃ h 1 ) ) ;

a ₂ ( - A 2 exp ( - ia ₂ h 1 ) + A ₂ ' exp ( ia ₂ h 1 ) ) = a ₃ ( - A ₃ exp ( - ia ₃ h 1 ) + A ₃ ' exp ( ia ₃ h 1 ) ) ;

P 1 ( A ₃ exp ( - ia ₃ h ₂ ) + A₃' exp ( ia ₃ h ₂ ) ) = P ₂ ( A 4 exp ( - ia 4 h ₂ ) + A ₄ ' exp ( ia ₄ h ₂ ) ) ;

<                                        \ V                                       .            (3)

a ₃ ( - A ₃ exp ( - ia ₃ h ₂ ) + A ₃ ' exp ( ia ₃ h ₂ ) ) = a ₄ ( - A ₄ exp ( - ia ₄ h ₂ ) + A 4 ' exp ( ia ₄ h ₂ ) ) ;

P ₂ ( A ₄ exp ( - ia ₄ h 3 ) + A ₄ ' exp ( ia ₄ h ₃ ) ) = P 1 A 5 exp ( - ia 5 h ₃ ) ;

a ₄ ( - A ₄ exp ( - ia ₄ h ₃ ) + A ₄ ' exp ( ia ₄ h ₃ ) ) = - a 5 A 5 exp ( - ia 5 h ₃ ) .

Здесь h 1 и h 3 – толщина стекла; h 2 – толщина воздушного промежутка.

Величина a во второй и четвертой средах (в элементах остекления) определяется a 2(4) = ia 2(4) I, где

I a ²⁽⁴⁾l c ₂^

sin² 9

—

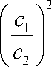
Здесь c1 и c2 – скорости звука в воздухе и стекле (соответственно), м/с. Тогда a, = a3 = a = 0,012 f,, 135    j a2 = a4 = 0,002 fj.

С учетом этого систему уравнений приведем к виду

A 1 + A 1 '= 1458 ( A 2 + A ₂ ' ) ;

6 ( — A 1 + A 1 ) = — A 2 + A ₂;

1458 ( A 2 exp ( - i 0,002 f j h ) + A 2 exp ( i 0,002 f j h ) ) = A 3 exp ( - i 0,012 f j h ) + A 3 ' exp ( i 0,012 fh ) ;

• - A exp ( - i 0,002 f j h ) + A ₂ ' exp ( i 0,002 f j h ) = 6 ( - A 3 exp ( - i 0,012 f j h ) + A 3 ' exp ( i 0,012 f jh1 ) ) ;

A 3 exp ( - i 0,012 f j h ₂ ) + A 3 ' exp ( i 0,012 f j h ₂ ) = 1458 ( A ₄ exp ( - i 0,002 f j h ₂ ) + A ₄ ' exp ( i 0,002 f j h ₂ ) ) ;

• <                                                                   ^V                                                         ’ (4)

• 6 ( - A 3 exp ( - i 0,012 f j h ₂ ) + A 3 ' exp ( i 0,012 f j h ₂ ) ) = - A ₄ exp ( - i 0,002 f j h ₂ ) + A ₄ ' exp ( i 0,002 f j h ₂ ) ;

1458 ( A ₄ exp ( - i 0,002 f j h 3 ) + A ₄ ' exp ( i 0,002 f j h 3 ) ) = A ₅ exp ( - i 0,012 f j h 3 ) ;

• - A ₄ exp ( - i 0,002 f j h 3 ) + A ₄ ' exp ( i 0,002 f j h 3 ) = - 6 A ₅ exp ( - i 0,012 f j h ) .

Приведенная система (4) состоит из 4 подсистем, каждая из которых содержит по два неизвестных: A k и A k _{+ 1} , а также промежуточные величины A k ' и A k _{+ 1} ' .

Введем обозначения:

A 1 1= Z - A 2 = Z  A 2 1 = Z ^ 21 = 7 ; A 3 = Z • A 3 ^ =

A1      1; A1      2; A1       3; A2      4; A2

A.'         A. A.'         A.'

344               45

.      ^Z 7 ;   . ^Z g ;     .      ^Z 9 ;     . ^Z 10 ;   . ^Z 11 ^.

A3       A3       A3        A4

Такие подстановки дают возможность исключить в каждой паре уравнений вспомогательные величины и вести вычисления в отношениях Z_m , m = 1, 2, …, 11. Покажем это на примере преобразований последней пары уравнений.

Поделим оба уравнения последней пары на A ₄ :

A

(

1458 exp ( - i 0,002 fh 3 ) +    exp ( i 0,002 fh 3 ) = A ^exp ( - i 0,012 fh 3 ) ;

^                      ^A 4                      ^A 4

- exp ( - i 0,002 f h ) + -4- exp ( i 0,002 f h ) = -6— exp ( - i 0,012 f h ) . ^j        A 4                   ^j            A 4                    ^j

;

С учетом введенных обозначений:

1458 ( exp ( - i 0,002 f j h 3 ) + Z ₁₀ exp ( i 0,002 f j h 3 ) ) = Z 11 exp ( - i 0,012 f j h 3 ) ; - exp ( - i 0,002 f j h 3 ) + Z ₁₀ exp ( i 0,002 f j h 3 ) = - 6 Z 11 exp ( - i 0,012 f j h 3 ) .

Решая эту систему методом подстановки, получаем:

7 =

A 4 1

A 4

- 8749 exp ⁽- i 0,0⁰⁴ fh ^{3 ) ;}

Z , = A ⁵ = 1458 (exp ( i 0,010 f h ) + Z ₀ exp ( i 0,014 f h )) .

^A 4 ^jj

Аналогично из остальных пар уравнений получаем Z1, Z2,...Z8 и можем найти t z z z tp ^11 ^8 ^5 ^2 , а, исходя и этого выражения, определяется звукоизоляция

ЗИ = ^10lg k1T

Заключение. Как видно из полученных выражений, конструктивными размерами элементов двойного остекления (в частности толщинами), как «слабого» звена в системе шумозащиты, можно добиться выполнения санитарных норм шума на рабочем месте оператора. Необходимая звукоизоляция в этом случае достигается рациональным подбором не только толщин стекол, но и воздушного промежутка между ним.