Расчетная модель подшипника скольжения

Введение. В настоящее время развитие машиностроения характеризуется увеличением в современных двигателях мощности поршневых и роторных машин. Повышение требований к их надежности и долговечности приводит к неизбежному росту нагруженности и сопряжений трибосистем. Ключ к решению этой проблемы лежит в совершенствовании конструкций узлов трения трибосистем. Наличие смазочного материала в трибосистемах обеспечивает режим жидкостного трения, при котором потери достаточно малы, а износ трибоузлов минимален. При разработке математических расчетных моделей и конструировании новых, а также при модернизации разработанных трибосистем необходимо уделять повышенное внимание происходящим процессам и явлениям, к которым относятся

*

**

механические, тепловые и химические процессы. Возникает необходимость в разработке новых расчетных моделей трибоузлов, обладающих большой маслоемкостью и демпфирующими свойствами [1–13].

Цель работы. Целью настоящей статьи является разработка расчетной модели трибоузлов с пористым покрытием при частичном заполнении рабочего зазора с учетом зависимости проницаемости и вязкости от давления.

Постановка задачи. Рассматривается установившееся движение трибосистемы с пористым покрытием. Вал вращается с угловой скоростью Q, а подшипник неподвижен. Пространство между валом и подшипником не полностью заполнено смазочным материалом (рис. 1).

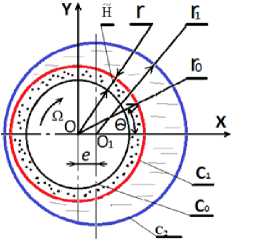
Рис. 1. Рабочая схема

Fig. 1. Functional diagram

В полярной системе координат с полюсом в центре вала уравнение контуров вала с пористым покрытием С ₀ и С ₁ и подшипниковой втулки С ₂ задается в виде:

С о : r = r 0 - H ; c i : r ' = r o ;

C 2 : r ' = r _r( 1 + H ) = r 1 + e cos9;

H = scos9-¹ s ² sin ² 9; s = -< 1

2                   r ₁

где r ₁ — радиус подшипника скольжения; r ₀ — радиус вала с пористым покрытием; H — толщина пористого слоя; H — толщина смазочного материала; e — эксцентриситет.

Зависимость вязкости и проницаемости задается в виде:

ц' = ц e ^a p\     к ' = к o e ^a p ,                                                 (2)

где ц₀ — характерная вязкость, к ₀ — характерная проницаемость пористого слоя; ~ — экспериментальная постоянная величина, р' — гидродинамическое давление в смазочном слое, ц' — коэффициент динамической вязкости смазочного материала, к' — проницаемость пористого покрытия.

Исходные уравнения и граничные условия.

Исходными уравнениями являются уравнения движения вязкой несжимаемой жидкости для случая «тонкого слоя», неразрывности и Дарси с учетом (2).

д ² и'    1 д р '     д V д и' „

—т =--—, — + = 0,

дr'2 ц' д9     дr' д9                                                        (3)

д ² р ' 1 д р ' 1 д ² р ' _п

Г +      + 2 Г = 0.

д r ² r д r   r ² д9 ²

Связь между размерными и безразмерными переменными задается в следующем виде: – в смазочном слое:

Машиностроение и машиноведение

– в пористом слое:

~ = —, и ' = Q r₀и , v ' = Q5 v , p ' = p * p , ц' = ц₀ц, P *

^r ' = r o +5 ^r , 5 = r i - ^r o , p * = ^ ⁰ f^ r ⁰ .

r ' = Hr • , k ' = k ₀ k , P ' = p • P .

Здесь u ', v ' — компоненты вектора скорости, p' — гидродинамическое давление в смазочном слое, P' —

гидродинамическое давление в пористом слое.

С учетом (4) и (5) уравнение (3) примет следующий вид:

д2и = 1 dp   dv + dw = 0  д2 P + J_ дP + 1 д2 P дr2 = eap д6,  дr + д6 = ,  дr*2 + r* дr* + r*2 д62

И соответсвующими граничными условиями:

и\ п = 1, v | п = - N-p-     ,

Ir=0            lr=0          ** r д r r* £l r i~

H

p ( 6 1 ) = p ( 6 2 ) = ⁰, p = ^P|_{г =} rL,

*

H

и = 0, v = 0 при r = 1 + n cos 6 ,

д p д r *

r ₀

= 0,

~

H

kr2    e где N = -° 0 , n = -

5 3 H 5

Решение функции тока (6), с учетом граничных условий (7), будем искать в виде:

и = ^- + U ( r , 6), v = -1^- + V ( r , 6), U ( r , 6 ) = ~ ( ^), V ( r , 6 ) = -~ ( ^ ) h ' ( 6), д r              д6

E = h (6),

V(r, 6) = Vfc), dp d6

~~

« p |^l

I h ² ( 6 ) h 3 ( 6 ),

Подставляя (8) в (6), с учетом (7), получим:

d ³ w ~   d ² и ~   dv  _v du      ¹

т = c2,  -7ТГ = c1,  "^ + ^7 = 0, fu(^)d^ = v(0)- d ^3        d^2        d^    d^      0

, p ( 6 1 ) = p ( 6 2 ) = 0, ~ ( 1 ) = 0, ~ ( 1 ) = 0.

* r r =—

H

~ ( 0 ) = 1, ~ ( 0 ) = - N |p д r

Решение задачи (9)–(10) находится интегрированием. В результате:

av_ £ 2. ( , 2

д^ 2 3

2 ~

м ( ^ ) = ~       I -1- + 1 1^ + 1.

12     2

Определение гидродинамического давления.

Для определения безразмерного гидродинамического давления в смазочном слое имеем:

~~

-a p ^dp _ ^c 1       ^c 2

d6 h2(6) h3(6) , где h (6) = 1 + n cos 6.

Введем обозначение:

z = e-ap и, продеффиринцировав обе части равенства по 6 , получим:

dz          dp dz

— = -ae ap — — = -ae ap — d 6         d 6 d 6

С учетом (14) уравнение (12) запишется в виде:

~~ dz | c1

II d6      (h2 (6) h3 (6)I

Интегрируя уравнение (15) с точностью до членов второго порядка малости O ( р ² ) , с

учетом

z ( 6 1 ) = z ( 6 2 ) = 1 , получим:

z = -а(~1 (6 - 2р sin 6) + ~2 (6 - 3р sin 6)) +1

или

Используя граничные условия z ( 6 1 ) = z ( 6 2 ) = 1 будем иметь:

-    ~ c 2 = - c1

^f   2pcos ^^sin ⁶ 2 ⁶ )

1 +  ----²----- 2—

6 2 -6 1

V

С учетом (17) уравнение (16) примет следующий вид:

z = -а q

psin 6

^^^^^^в

2p6 cos ^{6 2 + 6 1} sin ^{6 2}— ^{6 1}

6 2 -6 1

+1

V

(

e-аp = -а~1р

sin6

^^^^^^»

_   62 + 6 . 62-6Л

26 cos —---1 sin —---1

_______2_______2__

^^^^^^в

+1

V

Выполняя аналитическое разложение функции e ^{а p} в

ряд

Тейлора с точностью до членов

O (а2)

включительно, получим:

p = С1р

62+6

26 cos—---1

sin 62—

sin

2 6 |

6 2 -6 1

V

С учетом (20) давление фильтрующегося смазочного материала в пористом слое будем искать в виде:

p ( г * ,6 ) = R ( г * ) ~ 1 р sin6

^^^^^^в

™   62+6 . 62-6Л

26 cos—---1 sin —---1

__________2__________2

6 2 -6 1

V

Подставляя (21) в уравнение Дарси (6) для определения R (г *), приходим к следующему дифференциальному уравнению:

С граничными условиями:

R"(г*)

R ' R n

■ —= = 0

* r

r

, *2

dR

dr *

r

, *

r 0

~

H

= 0,

RI 20 | = 1

V h 7

Непосредственное интегрирование (22) с учетом (23) для функции R ( г * ) позволяет получить выражение:

R (г *)=

г о Нг *

2 г ₀ ² - 2 Нг ₀ + Н ²

г о ( г о ² - 2 Нг о + Н ² ) Н ( 2 г ₀ ² - 2 Нг ₀ + Н ² ) г *

Интегрируя уравнение неразрывности по ^ от 0 до 1, приходим к следующему уравнению:

^^^^^^в

N ^p 5 г *

* r

= J zZ(^)d ^

r 0      ₀

~

H

С учетом (11), (21) и (24) для c ₁ получим следующее выражение:

~ = 6 1 1 -12 NB\ 1

A 6 | sin 6 7

Машиностроение и машиноведение

где

.   62 + 6 . 62-6

2cos 2    1 sin 2    1

A =----- 2------ 2

6 2 -6 1

,

B = , H ⁽ 2 Г 0 J H ) .

Г ( 2 r 0 - 2 Hr + H )

Тогда, с учетом c ₁ , окончательно для гидродинамического давления получим:

( p = 6n (1 -12 BN )(sin 6-A 6)+12 BN I A 6

f                             I

^^^^^^в

A 2 6 ² +

sin 6 ^J _j

.

Определение несущей способности и силы трения.

С учетом (11) и (28) для составляющей вектора поддерживающей силы и силы трения получим выражения:

R y = p * r₀ J P sin 6 d 6 = 6n

ц ₀ О r ₀3 Г ( 1 -12 BN )

S2

( 6 ₂ -6 1 + 2 sin ( 6 ₂ + 6 1 ) sin ( 6 ₂ - 6 1 ))

-

62 +6, . 6,-6           6, +6, . 6,-6,

- 2 A ( 6, + 6, ) sin —---¹ sin —---¹ + 2 A cos —---¹ sin —---¹ +

21     _{2      2         2      2}

12 BN | 2 A ( 6 ₂ +6 1 ) sin ^{6 2} + ^{6 1} sin ^{6 2} 2 ^{6 1} -2 A cos ^{6 2} + ^{6 1} sin ^{6 2} 2 ^{6 1} - A3- ( 6 ₂ -6 1 ) 3 )

^R x = p * ^r 0 J P ^{cos 6} d ⁶ = 6П ^r ^{0 ( 1 12 BN} ) ^{f 1sin (6} 2 ^{+ 6} 1 ^{) sin (6} 1 ^-6 2 ⁾ 9 ,                    О L ² f²

_{= Ц} 0 ^ r 0

L mp     о

S

.(^           6, +6 . 6,-6,

- A I ( 6 ₂ - 6 1 ) 2 cos 2 2 ¹ sin 2 2 ¹

12 BNA I ( 6 ₂

-

6 1 ) 2cos

6 ₂ +6 1

sin 2

-

2sin

- 6 ₁

6 ₂ +6 1

-2sin

sin 1

-

6 ₂ +6 1 . 6

sin

-

+

6 2 r_v" ( 6 ) ~' ( 6 ) )

Ц +       d 6

e . f h ² ( 6 ) h ( 6 ) J

Ц 0 ^ r 0

S

^^^^^^B

, a 2

1 + a p + — p

~ 1 ( 1 + A n )

62+6 . 61-62)+

6, -6, + 4nsin—---Lsin—---2 I

211    2       2 J

f~ .)(             62+6 . 6-62)

+ ¹ +1 6,-6 + 6n sin—---^Lsin—--- 2

f 2 Jf 2 1             2          2 J

На основании численных расчетов построены графики, приведенные на рис. 2, 3.

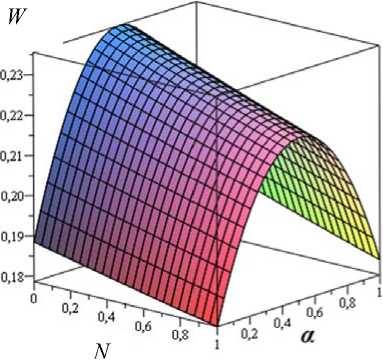
Рис. 2. Зависимость несущей способности от параметра α, характеризующего зависимость вязкости от давления и параметра N , характеризующего проницаемость пористого слоя

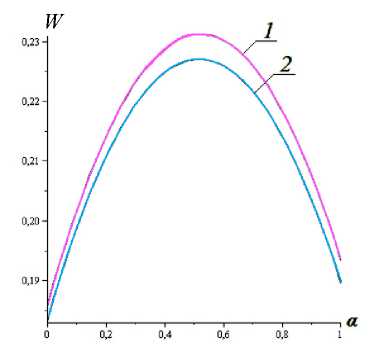
Рис. 3. Зависимость несущей способности от параметра α, характеризующего зависимость вязкости от давления: 1 — N = 0,25; 2 — N = 0,5

Fig. 2. Bearing resistance – parameter α relation characterizing the viscosity – pressure and parameter N relation, characterizing porous layer permeability

Fig. 3. Bearing resistance – parameter α relation characterizing the viscosity – pressure relation: 1 — N = 0,25; 2 — N = 0,5

Выводы:

• 1.    С увеличением параметра α, характеризующего зависимость вязкости от давления, несущая способность подшипника имеет экстремум, что приводит в этой области к снижению силы трения.

• 2.    С увеличением параметра N , характеризующего проницаемость пористого слоя, несущая способность и сила трения резко уменьшаются.