Расчетная модель радиального подшипника повышенной несущей способности, работающего на микрополярной смазке с учетом ее вязкостных характеристик от температуры

Введение. Как известно, в настоящее время в качестве модели гидродинамической смазки подшипников скольжения широко используется микрополярный жидкий смазочный материал. Поэтому разработка методов расчета подшипников скольжения, работающих на микрополярном жидком смазочном материале, требует учета зависимости вязкости не только от давления, а также зависимость вязкостных характеристик от температуры. Значимый недостаток существующих методов расчета подшипников скольжения, работающих на микрополярном жидком смазочном материале, состоит в том, что в большинстве случаев или вовсе не учитывается зависимость вязкости от давления и температуры [1–7], или учитывается эта зависимость только от давления [8–11].

Постановка задачи. Рассмотрим установившееся движение микрополярного смазочного материала в зазоре радиального подшипника. Предполагается, что подшипник с адаптированным профилем опорной поверхности неподвижен, а вал вращается с угловой скоростью Ω (р_ис. 1).

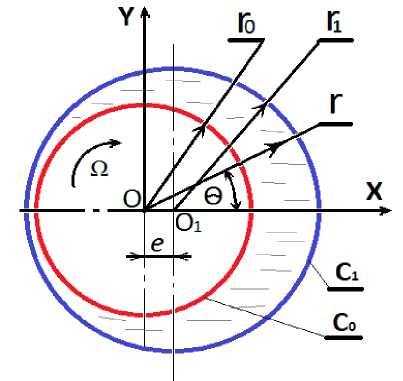
Рис. 1. Расчетная схема радиального подшипника

Предполагается, что имеет место частичное заполнение смазочным материалом рабочего зазора (т. е. наличие свободной поверхности). Кроме того, предполагается, что вязкостные характеристики микрополярной жидкости зависят от температуры.

- β ′ Т ′                     - β ′ Т ′                    - β ′ Т ′

μ = μ₀ e ,κ = κ₀ e ,γ = γ₀ e                           (1)

Здесь μ0 — характерная вязкость ньютоновского смазочного материала; κ0и γ0 — характерные вязкости микрополярного смазочного материала;

T ′ — температура, β ′ — экспериментальная постоянная величина.

Уравнение контуров вала и подшипниковой втулки в полярной системе координат r ′ , θ в центре вала запишутся в виде:

r ′= r ₀, r ′= r ₁ + e cos θ - а sin ωθ ,                                            (2)

eа где r — радиус шипа; r — радиус подшипника; e — эксцентриситет; ,  — малая величина одного порядка (

0               1                                       δδ

δ= r ₁ - r ₀); ω — параметр контактного профиля подлежит определению.

Основные уравнения и граничные условия. В качестве исходных уравнений берется система безразмерных уравнений движения микрополярной жидкости для случая «тонкого слоя» с учетом (1), а также уравнение неразрыв-

ности:

∂ 2 u   ∂ υ1 dp 2 ∂ r 2 + N ∂ r = e - β T d θ ,                                                      (3) ∂ 2υ υ 1 ∂ u      ∂ u ∂ v 2 =  +     ,      += 0. ∂ r 2    N 1 N 1 ∂ r     dr ∂θ

Здесь размерные величины u ′ , v ′ , υ′ , p ′ , µ′ , κ′ , γ′ , τ′ , T ′ , r ′ связаны с соответствующими безразмерными u , v , υ , p , κ , γ , T , r следующими соотношениями:

u ′= u Ω r 0 ; μ=μ0μ;	v ′= Ωδ v ;      ν′= ν∗ν ;      p ′= p ∗ p ; κ=κ0κ;    γ=γ0γ;     Т ′= Т 0 Т ;     r ′= r 0 +δ r ;
∗ r Ω υ = 0 , 2 δ	p ∗= r 02 Ω ( 2 µ 0 + κ 0 ) , δ= r - r ;                                             (4) 2 δ 2

N ² =     ^{κ 0} ; N 1 = ^{l 2 2} µ ⁰ ; l ² = γ ⁰.

2μ₀ + κ₀          δ ²κ₀        4 µ ₀

Здесь u′, v′ — компоненты вектора скорости; υ′ — скорость вращения микрочастиц, T0 — характерная тем- пература.

Как видно из системы (3), помимо обычных безразмерных параметров, встречающихся в теории ньютоновской жидкости, здесь вводятся и другие параметры для микрополярной жидкости.

Параметр взаимодействия N → 0 при κ₀ → 0.

Безразмерный параметр N ₁ зависит от параметра l , имеющего размерность длины, и его можно трактовать

Г 5)

как характеристику, зависящую от размера молекул смазки. Система уравнений (3) с точностью до членов O к ro J решается при следующих граничных условиях:

e n =

u = 0,	v = 0,	и = 0	при r = h ( e ) = 1 + n e- П 1 sin^ e ;
u = 1,	v = 0,	и = 0	при r = 0;
P = ( 0 )	при	e = e 1	и e = e 2;	(5)

a ni =5;

θ1 и θ2 — соответственно координаты начала и конца свободной поверхности. Осредним второе уравнение системы (3) по толщине смазочного слоя. Получим:

1 h d 2V,      1 h ,     1 h д UJ dr = v dy +        di h 0 dr2     N1 h 0 N1 h 0 dr

Найдем решение уравнения (6) в виде:

и = a1 (e) r2 + a2 (e) r+a3 (e).

Из граничных условий (5) следует, что

A 3 = 0;     A ₂ = - A 1 h .

С учетом (8) для и получим выражение:

u = A1 (e)-( r2

- rh).

r

Подставляя (9) в (6) с точностью до членов О n I, О П1'^_— I, О I’ получим: I       N 1 I ¹ Л fl лг² I

к

N 1

N 1

и = —— f r ² - 2 h\ , 2 N ₁

2 u = - ( 2 r - h ) . d y    2 N 1^{v      7}

С учетом (10) система уравнений (3) в принятом нами приближении преобразуется к следующему виду:

eβT dp d e

a 2 u a r 2	- N - ( 2 r - h ) = 2 N 1
u = -	—— f r 2 - rh ), 2 N 1
d u	a v  n
+	— = 0.
ae	a r

Точное автомодельное решение системы (11) с граничными условиями (5) будем искать в виде:

V(r,e) = -v(5)he,

^{U ( r} , ^e ) = ^u < ⁵ ) ,      ⁵ = h ,

V ( r , ^e ) = V ( ⁵ ) ,

e

~

C 2

β T dp    C 1

I ’ de h2(e) h3(e)

и = —— (52 - d.

2 N ₁

С учетом (12) из системы (11), получим:

V m = С2,    u"(4 ) = C + 2N- (24 -1), u -+4 v = 0,    u = —IN (42- 4), dp=e-вт   C + C2

d 9         ( h ² ( 9 ) h ³ ( 9 ) ^ ^.

Граничные условия (5) примут вид:

v‘(0) = 0, V'(1) = 0;     u(0) = 1,     v(0) = 0, u (1) = 0,     v (1) = 0,

} u ( 4 ) d 4 = 0,      p ( 9 i ) = p ( 9 2 ) = 0.

Решая задачу (13) - (14) непосредственным интегрированием, получим:

Здесь С 1 = 6 -

N ²

N 1

~

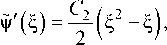
4²    N ² f 4³

u ( 4 ) = С +

1 2   2 N , I 3

42) f N2

+—

2 J (12 N1

— 1 1 4 + 1,

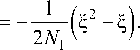
а С ₂ в дальнейшем определим из условия p ( 9 1 ) = p ( 9 2 ) = 0 .

Как и ожидалось, при N 1 ^ м , v ^ м полученные результаты полностью совпадают с результатом для случая ньютоновской смазки.

Для определения гидродинамического давления имеем:

β Т dp    C 1 C 2

e                                     1                   .

d 9 h ² ( 9 ) h ³ ( 9 )

Для решения этого уравнения необходимо вначале найти функцию ц = —ву . Воспользуемся выражением для скорости диссипации энергии под действием сил сдвига. Получим dH- = 2popQ2-0h1 d 9 =      " J

V

u - ( 4 )

0 ( h ² ( 9 ) + h ( 9 )

) 2

■ d 4.

Повышенная температура будет определяться выражением.

dT ‘ dH ‘    1      1   2ц 0 ц П ² - 0 ² h ( 9 )

-----=-----•-----=-----•-------------------

v"( 4 ) ^W( 4 )

d 9    d 9 c p Q  c p Q

0 ( h ² ( 9 ) ¹ h ( 9 )

) ²

-   d 4.

Здесь Q — расход смазки в единицу времени; c_р — теплоемкость при постоянном давлении.

Q = Q - o 6J v ‘ ( 4 ) d 4 =

—6Q - 0 C ₂

.

Продифференцируем по 9 зависимость ц от температуры Т :

dμ

= — №.

d 9

Комбинируя (18) - (20), получим:

p² ( 9 ) d 9

Введем следующие обозначения:

d p = 240p „ Q - h ( 9 ) ¹ f И4 )

С 2 c p 6 2 Т 0

K =

u( 4)

!( h ² ( 9 ) ' h ( 9 )

24РЦ о 2 - о

h 0 ² c p Т 0

.

) ²

■   d 4.

Ц ^(o) =

A - = J ( у "( 5 ) ) d ^ = 72 , A ₂ = J 2y "( § ) U ( § ) d § = -C₂ C - , 0 12          0 6

A₃ = J( u') d ^ =----+ 4

N ² --+

N 1

N ⁴

12 N ₁² .

Здесь K — тепловой параметр.

С учетом (22) уравнение (21) преобразуется к виду:

1   dμ ц2 (o) d°

„ 2A

K A-   . A2.

-^— —---1-----1■—-

(^h ³ ( o ) h ² ( o ) h ( ° ) J

Интегрируя уравнение (23), получим:

1 - К [ J з ( 0 ) A 1 + J 2 ( 0 ) A 2 + J - ( 0 ) A 3 ]

С ₂

J (o) = ° -d°-к ( ) °- hK (°)

Гидродинамическое давление p с учетом (24) определяем из уравнения (16).

~

P = C-

° ^ц^ + C 2 ° ^ = C - J 2 ( ° ) + C - 2 J 3 ( ° ) =

(°)        01 h (°)

{ ( ° —° 1 ) —n ( ° —° 1 ) 2 — —^cos to ( ° —0 1 ) —

—

	° - h
	N 2 )
[ 6 —
	N TJ
( ° 2	—° - )

'² +П ( ° 2

—

°- )3 + n1 (°2 °-) cos m(°2 — °-) to

x

x

⁽° ^—° - ^)— -П' | ° ° - ) ^— — cos ^to(° 2 ^—° - ) 2                to

Перейдем к определению основных рабочих характеристик радиального подшипника.

Для безразмерной несущей способности и безразмерной силы трения с учетом (25) получим:

R y

—

ro^( 2Цо + Ko) 252

° 2

J p sin ° d ° , ° -

R x

? o Q⁽ 2 Ц о + ^Ko ) 2 5 ²

° 2 J ° -

p cos ° d ° ,

L тр

^G^rb 5

° 2 6₂ d °   f 7 ^ ²    ^° 2 d °

² + 4

° -     2 h ² ( ° ) ( -2 ^ -     J ° - h ( ° )

Входные параметры для расчета несущей способности и силы трения, определяемые выражением (22) - (26), приведены в таблицах №1 и №2.

Таблица 1

Входные параметры для расчета несущей способности и силы трения

~ J -	~ J 2	~ J	η=η1	N	N 1	ω	β	K	° 2 —° -
7, 6	7,12	2,8	0,01	0,95	100	0,5	0,7	0,8	-5 °
7, 4	7,10	2,82	0,01	0,95	200	0,5	0,8	0,9	-5 °
7, 8	7,14	2,84	0,01	0,95	00	0,5	0,6	0,7	-5 °
14,02	1 ,22	5, 77	0,01	0,95	100	0,5	0,7	0,8	30 °
14,006	1 ,21	5, 58	0,01	0,95	200	0,5	0,8	0,9	30 °
14,04	1 ,24	5, 96	0,01	0,95	00	0,5	0,6	0,7	30 °

Таблица 2

Входные параметры для расчета несущей способности и силы трения

A t	A 2	A 3	N	N 1	ω	η=η1	β	K
0,003	0,1997	3,99	0,95	100	0,5	0,01	0,7	0,8
0,0033	0,1998	3,995	0,95	200	0,5	0,01	0,8	0,9
0,0033	0,1999	3,997	0,95	300	0,5	0,01	0,6	0,7

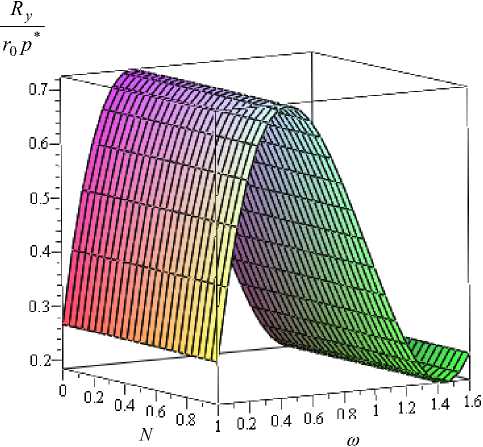
Рис. 2. Зависимость безразмерной несущей способности от параметра связи N и параметра ω

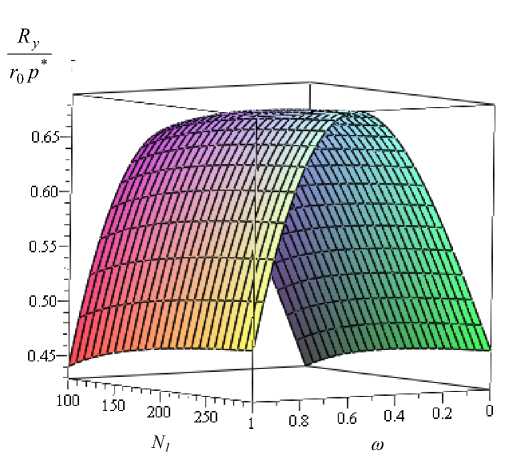
Рис. 3. Зависимость безразмерной несущей способности от параметра N ₁ и параметра ω

R y

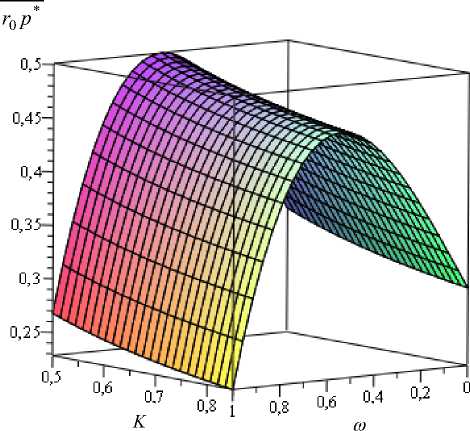
Рис. 4. Зависимость безразмерной несущей способности от теплового параметра К и параметра ω

Выводы. Результаты численного анализа, приведенные в табл. 1, 2 и на рис. 2–4 позволяют сделать следующие выводы.

• 1)    Основные рабочие характеристики подшипника существенно зависят от:

• —    параметра ω , характеризующего адаптированный профиль опорной поверхности;

• —    теплового параметра К ;

• —    экспериментального параметра β , обусловленного зависимостью вязкости от температуры Т.

• 2)    С увеличением теплового параметра К несущая способность подшипника уменьшается. Наиболее резкое уменьшение отмечается при К< 0,5. При К> 0,7 несущая способность стабилизируется. С увеличением параметра N 1 и параметра ω , характеризующего адаптированный профиль опорной поверхности, несущая способность увеличивается. Параметр связи N не оказывает существенного влияния на несущую способность. При значении параметра ω =0,5 наблюдается ярко выраженный максимум несущей способности. При N ₁ →∞ значение несущей способности стремится к соответствующему значению несущей способности для случая ньютоновского смазочного материала.