Расчетная модель радиального подшипника, смазываемого расплавом, с учетом зависимости вязкости от давления

Введение. В современном машиностроении трибоузлы для новых машин проектируются, как правило, с учетом увеличения статических и ударных нагрузок, действующих на опоры скольжения. Следует отметить, что одним из важнейших конструктивных элементов подшипников жидкостного трения является смазочная среда.

Одним из методов решения конструктивно-эксплуатационных задач может быть применение смазывания расплавом легкоплавкого покрытия подшипниковых втулок.

В настоящее время существует значительное число технологий диффузионной металлизации, большинство из которых являются сложными, требуют применения дорогостоящего оборудования, что делает их промышленно нереализуемыми. На этом фоне выгодно отличается технология диффузионной металлизации сталей из среды легкоплавких жидкометаллических растворов. Ее перспективность связана с простотой реализации, возможностью использования стандартного термического оборудования, совмещения данной технологии с термической обработкой покрываемых изделий и т. п. Однако самое главное — возможность получения качественных изделий и регулирования свойств покрытий за счет варьирования технологических режимов.

Диффузионная металлизация из среды легкоплавких жидкометаллических растворов основана на явлении селективного изотермического переноса металлических элементов на металлические материалы [1–4]. Технологически данный процесс осуществляется путем погружения и выдержки изделий в легкоплавком расплаве, содержащем в растворенном состоянии элемент, на базе которого формируются диффузионные покрытия.

Использование данной технологии позволяет получать на поверхности изделий однокомпонентные и многокомпонентные диффузионные покрытия на базе различных металлических элементов.

Смазывание жидкими металлами применяют при температурах, при которых обычные смазочные среды претерпевают необратимые физико-химические изменения. Преимущество смазывания расплавом состоит в том, что смазочный материал образуется в области контакта, где это необходимо. Плавление доставляет достаточное количество смазочного материала в зону трения, механические и конструктивные сложности, связанные с его подачей, отсутствуют. Смазывание расплавом изучалось во многих прикладных задачах, в частности в процессах формоизменения и резания металлов [5–7]. Большое количество работ [8–14] посвящено гидродинамическому расчету радиальных подшипников бесконечной длины в условиях отсутствия смазочного вещества и учета зависимости вязкости смазочного материала от давления. Существенным недостатком рассматриваемой пары трения, работающей на смазывании расплавом, является низкая несущая способность. Кроме того, процесс смазывания не является самоподдерживающимся.

Таким образом, разработка расчетной модели подшипников скольжения, работающих на смазочных материалах в виде металлических расплавов, с учетом вышеуказанных аспектов функционирования, представляет собой одно из перспективных направлений теоретических исследований современной трибологии. Последнее определяет новизну и актуальность полученного решения.

Научная новизна предлагаемого решения и уточнения расчетной модели заключается в оценке влияния параметра, обусловленного расплавом легкоплавкого покрытия подшипниковой втулки, и параметра, характеризующего зависимость вязкости смазочного материала от давления, обеспечивающих опорам скольжения аномально низкий коэффициент трения.

Цель работы: формирование уточненной расчетной модели опоры скольжения в режиме гидродинамического смазывания при наличии смазочного материала и расплава легкоплавкого покрытия подшипниковой втулки с учетом зависимости вязкости смазочного материала от давления.

Постановка задачи. Рассматривается модель установившегося движения вязкого несжимаемого смазочного материала в рабочем зазоре бесконечного радиального подшипника скольжения, покрытого легкоплавким расплавом.

Вал вращается с угловой скоростью Q , а подшипниковая втулка неподвижна. Предполагается, что пространство между эксцентрично расположенными валом и подшипником полностью заполнено смазочным материалом, а подшипниковая втулка выполнена из материала с низкой температурой плавления.

Рассматриваются условия, когда все тепло, выделяющееся в смазочной пленке, идет на плавление поверхности материала подшипниковой втулки.

Задается следующая зависимость вязкости смазочного материала от давления:

ц' = Ц о е“^Р ,                                                             (1)

где ц0 — характерная вязкость; ц ' — коэффициент динамической вязкости смазочного материала; р' — гидродина мическое давление в смазочном слое; а — постоянная.

Исходные уравнения и граничные условия. Движение смазочного материала описывается уравнением течения вязкой несжимаемой жидкости в приближении для тонкого слоя и уравнением неразрывности:

52vв _ dp'

^Ц д r ' 2     d в ,

^+2k+1 ^ = о дr' r' r' дв

Здесь v _e, v_r ‘ — компоненты вектора скорости смазочной среды; p' — гидродинамическое давление в смазочном слое; ц' — коэффициент динамической вязкости.

Рассмотрим полярную систему координат с полюсом в центре подшипниковой втулки (рис. 1).

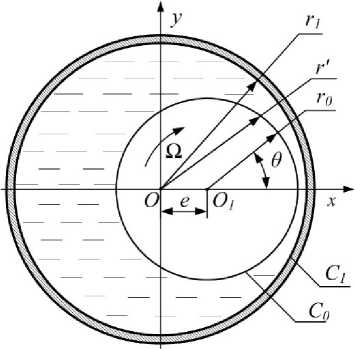
Рис. 1. Расчетная схема радиального подшипника с легкоплавким покрытием

Fig. 1. Analytic model of radial bearing with fusible coating

В этом случае уравнения контура вала расплавленной поверхности легкоплавкого покрытия подшипниковой втулки и поверхности подшипниковой втулки, покрытой металлическим расплавом, запишем в виде:

r' = ro (1+ H), r' = ri, r' = ri +Kf(в),

^где H = e cos в -¹ e ²sin² в + ..., 2

e

e =—;

r ₀

r ₀ — радиус вала; r ₁ — радиус подшипниковой втулки, покрытой металли-

ческим расплавом; e — эксцентриситет; e — относительный эксцентриситет; X f ( в ) — ограниченная функция при в G [ 0 G 2п ] подлежит определению.

Граничные условия в рассматриваемом случае с точностью до членов O (ε²) запишем в виде:

v _в= 0, v_r ■ = 0 при r' = r 1 +X f ( в ) ;

v _в= r ₀ n , v_r ■ = - П e sin в , при r' = r ₀ + e cos в ;

P ' ( ⁰ ) = P ' ( ^{2 п}) = P * .

p

Машиностроение и машиноведение

Для определения функции Xf (0), обусловленной расплавленной поверхностью подшипника, воспользуемся формулой скорости диссипаций энергий:

d X' f ( 0 ) r d 0

r + e cos 0

■QL ' = 2ц  J r1+Xf (0)

^{5 v} 0

5 r '

I dr \

где L ' — удельная теплота плавления на единицу объема.

Переход к безразмерным переменным реализуется на основе следующих формул:

r ' = r ₁ -8 r , 8 = r ₁ - r ₀; v_e = Q r ₀ v ; v_r . =Q Su ;

,           _ a ц =цоц; a = —. p ып Qr2

p = p p ; p = 2 ; δ

Выполняя подстановку (6) в систему дифференциальных уравнений (2) и (5), а также в граничные условия (4), придем к следующей системе дифференциальных уравнений:

5p      a2 v    ap dp     au

= O; = - e ; 1= O;

5r      ar2       de     ar dXf(0)   ЛпГ0'дv^2

= - K          dr,   K =0

d 0         -nif Wl dr J

и граничным условиям:

v = 1,

u = - n sin 0 , при r = 1 - n cos 0 ;

v = 0,

u = 0 при r = 0 -Ф ( 0 ) ; p ( 0 ) = p ( 2 n ) =

p g

* , ^p

где n = e ; n i =^X ; ф ( 0 ) = П 1 f ( 0 ) . 8        8

Пусть Z = e ^{–α p} . Продифференцировав обе части равенства, получим:

— = - a e ^{- a} p d 0

Тогда уравнения (7) и (8) примут следующий вид:

d ² v

dp или d 0

1 dZ

;

dr ²     a d9

7 d ^ф ( ⁰ )- К

Z = - K d 0

–

e ^{- a} p

dp 1 dZ

–

d 0    a d 0

a u   a v   „

+ = 0;

ar  a e os0( 5v0 )2 , I 0 I dr

с соответствующими граничными условиями:

v = 1, u = - n sin 0 , при r = 1 - n cos 0 ;

.

p _g

-a v = 0, u = 0 при r = 0 -Ф(0); Z(0) = Z(2n) = e p

.

В качестве малого параметра принимая K , обусловленный расплавом и скоростью диссипации энергии, будем искать функцию Ф ( 0 ) в виде:

Ф( 0 ) = - К Ф 1 ( 0 ) - К ² Ф₂( 0 ) - к 3 Ф₃( 0 ) - ... = н

где H = - К Ф 1 ( 0 ) - К ² Ф ₂( 0 ) - К ³ Ф₃( 0 ) - ....

виде:

Граничные условия для безразмерных компонентов скорости u и v на контуре _r = _- ф ( 0 ) можно записать в

u (0 - н ( 0 )) = v (0) -	'd v .5 r.	н ( 0 ) - r =0	'д 2 v Л drг <  r 7	н 2( 0 ) - . r =0	. = 0
u (0 - H ( 0 )) = u (0) -	'д м <5 r.	H ( 0 ) - r =0	' д 2 u <5 r 2	H 2( 0 ) - . r =0	.. = 0

Асимптотическое решение системы дифференциальных уравнений (10)–(11) с учетом граничных условий (12) и (14) будем искать в виде рядов по степеням малого параметра К :

v = v 0 ( r , 0 ) + Kv 1 ( r , 0 ) + K 2 v 2( r , 0 ) + ...; u = u 0 ( r , 0) + Ku 1 ( r , 0) + K 2 u 2 ( r , 0) +...; Ф ( 0 ) = - K Ф , ( 0 ) - K 2 Ф 2 ( 6 ) - K 3 Ф 3 ( 6 ) - _ ; Ф( 0 ) = - К Ф1( 0 ) - К 2 Ф2( 0 ) - К 3 Ф3( 0 ) - ...; Z = Z 0 + KZ 1 ( 0 ) + K 2 Z 2 ( 0 ) + K 3 Z 3 ( 0 ) ...                                           (15)

Выполняя подстановку (15) в систему дифференциальных уравнений (10)–(11) с учетом граничных условий (12), получим следующие уравнения.

Для нулевого приближения:

^{d 2} v о _ 1 dZ о      a v о a u о

	---=---, ---+--= 0                                            (10) d r 2      a d 0     d0   d r
с граничными условиями	v 0 = 1, u 0 = - n sin 0 при r = 1 - n cos 0 ; v 0 = 0, u 0 = 0 при r = 0;                                                        (17) - a pE Z 0 ( 0 ) = Z 0 ( 2 n ) = e p .
Для первого приближения:	d 2 v     1 dZ    d v   d u 1    = -      1 ; 1 + 1 = 0; 3r2    a d 0   d0   d r ,                                                    (18) d Ф 1 ( 0 ) i - n c os 0(9 v 0 ) - Z        =          0 dr 0 d 0        0 la r J
с граничными условиями	v 1 =fd v ° 1 'Ф > ( 0 ) ;      u 1 =fd u ° J   'Ф > ( 0 ) ; a r                     v a r r = 0                                     r = 0 v 1 = 0;    u 1 = 0 при r = 1- n cos 0 ;

Z 1 ( 0 ) = Z 1 ( 2 n ) = 0; K Ф 1 ( 0 ) = K a , Ф ( 0 ) = Ф ( 2 п ) = а .

Точное автомодельное решение. Точное автомодельное решение задачи для нулевого приближения будем искать в виде:

^v 0 = ^d^ ° ⁺ V 0 ( r , ⁰ ) ; u 0 =^-d^ r ⁺ U 0 ( ^r , ⁰ ) ; d r                    d0

V 0 ( r , ⁰ ) = V 0 ( ⁵ ) ; ⁵= ^r ;

• 1-    n cos 0

  
  

  V ( r , 0 ) = v ( 5 ) ;

  
  

U0 (r, 0) = - ц, (5)-h '(0);

dZ₀ Г

----= -a -d 0

w

~ A

C 2

l

+ h2(0) h3(0)

; h (0) = 1- n cos 0-

Подставляя (20) в систему дифференциальных уравнений (16) с учетом граничных условий (17), получим сле-

дующую систему дифференциальных уравнений:

V 0 = C 2 ; v 0 = C; u 0 ( E ) - Ev 0 ( $ ) = 0

и граничные условия:

v 0 ( 0 ) = 0,   v 0 ( 1 ) = 0,    u 0 ( 1 ) = -n sin 0,    v 0 ( 1 ) = 0;

U 0 ( 0 ) = 0,     v 0 ( 0 ) = 1,     J v 0 ( 5 ) d 5 = 0.

Непосредственным интегрированием получим:

^w

w

v0(5) =C2(e-5), v(5) = C5—11+C^b1, C = 6.

Из условия Z ₀ ( 0 ) = Z ₀ ( 2 n ) =

pg

-a -4

ep

получим следующее выражение:

Машиностроение и машиноведение

BV

С 2 = - C 1

2П d 9

^J h ² ( 9 ) 12 ( 1- n ’ ) ------- —--

1’7 d 9         2 + n ’

J h3(9)

.

Определение гидродинамического давления. С учетом (24) для Z 0 получим:

- a pg, Z 0 = - a ( C 1 J 2 ( 9 ) + C 2 J 3 ( 9 ) ) + e p

6a sin 9

( 2 + n ’ ) ( 1- П cos 9 )C + ( 1- П cos 9 )

pg

- a -4

+ e p

.

Общеизвестно, что в случае решения задачи плоской гидродинамической теории смазки давление определяется с точностью до произвольной постоянной. Значение этой постоянной С ₂ устанавливается из условия отсутствия отрицательных значений давления в смазочном слое.

Для нахождения значения Z для первого приближения необходимо сначала определить функцию Ф 1 ( 9 ) .

Для определения Ф 1 ( 9 ) с учетом уравнения (22) придем к следующему уравнению:

d Ф1 (9) = h (9)1 Гч-0 (S) + v0 (S))’ d9      Z0 0^ h2 (9) h(9)/ d S.

Интегрируя уравнение (26), получим:

9 A 1 d 9     9 A ’ d 9    9 A ₃ d 9

¹       0 Z ₀ h ³ ( 9 ) ⁺ 0 Z ₀ h ² ( 9 ) 0 Z 0 h ( 9 ) ,

1          2        C ’

где A1 = J(v"(s)) ds=4;

A’ = J 2-(s)-v ‘(S) d S =1CC2;

A 3 = J ( v ‘ ( s ) ) ² d s = 4;

sup Z 0 = sup

[ 0 : 2n ]

6a sin 9

sup

[ 0:2n ] ( 2 + n ’ ) ( 1- n cos 9 )

(1- n cos 9)

pg

-a

p

Решая уравнения (27)-(28) с учетом Ф 1 ( 0 ) = a , получим:

1 4 ( 1 + ’ n ² )

Ф (9) =--7------21( ) 64 (2 + n’)

6n(2n2 +1)

sin 9

6 (1-n2)

sin 9

/        Л \ 2 ,                , + /        л x 2 ,                ,2

(2 + n ) (1-ncos 9) (2 + n ) (1-Пcos 9)

+ a.

Точное автомодельное решение задачи для первого приближения будем искать в виде:

v1 =■?■+V (r,9); u = dr

^^^^^^B

-1 (r, 9) = — (S); S =

+ U (r, 9);

de 1' '

r

1- n cos 9 ’

V (r, 9) = v (s); U1 (r, 9) = - U1 (s)-h ‘(9);

dZ

1 = -a d 9

C 1 + C 2 h ² ( 9 ) h ³ ( 9 )

; h ( 9 ) = 1- n cos 9 .

Подставляя (30) в систему дифференциальных уравнений (18) с учетом граничных условий (19), получим следующую систему дифференциальных уравнений:

и граничные условия:

- №) = С2;

-(0) = 0,

u1 (0 ) = 0,

V44 = C1; z^HV‘(S) = 0

-; (1) = 0,   u 1 (1) = 0,   V1 (1) = 0;

V (0) = M,

J V (S) d S = 0.

Непосредственным интегрированием получим:

*;«)=C (s’- ^),

»

V1 (S) = C14+ 4-M S+M, C1 = 6M. Ай         Ай

к 7

где

Из условия Z 1 ( 0 ) = Z 1 ( 2 п ) = 0 получим следующее выражение:

M = sup

9е [0:2 п ]

х

С 2 = —

12 M ( 1- п ² )

2 + п2 ,

d v o д r

r =0

■Ф 1 ( 6 )

–2 -------+

sup

9е [0:2 п ] 1 — П COS 6

6 ( 1- n ² )

( 2 + п 2 ) ( 1- n cos 6 ) 2

1 ( 4 ( 1 + 2 п ² )

64 (2 + п2)

6n(2п2 +1) sin 6

( 2 + п 2 ) ( 1- n cos 6 )

6 ( 1- п 2 ) sin 6

(2 + п2) (1- n cos 6)2

^-

+ а

С учетом (34) для Z 1 получим:

Z 1 = - а| C 1 J 2 ( 6 ) + C 2 J 3 ( 6 )

6 а M sin 0    1          1

т.---^гт------4 п+т;-----^ (2 + п )(1-Пcos6)1 (1-ncos6)

Тогда для Z = Z 0 + KZ 1 получим следующее выражение:

Z =

6 а sin 6       I

-------;------------ П +

( 2 + п )( 1- П cos 6 ) (

pg

]              -а -4

---------- ( 1 + KM ) + e p

(1-n cos 6) J

или e ^{а P}

pg

- а -4

= Аа ( 1 + KM ) + e p

где Δ =

6sin 6

( 2 + n 2 ) ( 1- П cos 6 )

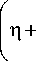
( 1- n cos 6 )

p _g

^-а - *

Применяя разложение в ряд Тейлора для функций e ^{–α p} , e ^p , получим:

22            2      ²

а P         pg а ( pg |

1- а p + —— -1 + а — * -     g =аА ( 1 + KM ) .

² P ² I P ^J

I P g I

Решая уравнение (37) с точностью до членов O (α)³, O (ξ)², O _* для гидродинамического давления, полу- I P ^J

чим

P

Pp p = -4-А ( 1 + KM ) 1 + а -4-

P

p

а2 (Pg | *

² I P J

.

Результаты исследований и их обсуждение. Перейдем к определению основных рабочих характеристик подшипника.

С учетом (16), (18) и (38) для составляющей вектора поддерживающей силы и силы трения получим:

Rу

= ^ ⁰ g r ⁰²4 p - Pg^ ) sin 6 d 6 =

2* 5 o I P J

6 ц ₀ О r _o 3 n ( 1 + KM ) ( n ( 1- П 2 ) + 1 )

5 2 ( 2 + n 2 )I1- П 2 ) 3 (

, P_g а ² ( Pg |

1 + а "4-— "4

P ² ( P J

;

j = ^ o ^ ^r o т_Р - 5

² П д v₍

I

д r

r =0

д v1 д r

r =o

_{d 6}= 4яц 0 П т 2

- ( 1 + 2 KM ) ³ ( ^1- П 2 ) ( 1 ^{+ KM} ) V¹"^ ( 2 + n ² )^( 1- n 2 ) 3

, а p

1- а p + — 2—

.

R х

= ^ r - 2f⁽ P - P g r¹ cos 6 d 6 = 0.

2*

5 o I P J

Для проверочных расчетов на основе полученных теоретических моделей использованы следующие значения:

μ 0 = 0,00595 Нc/м²; η = 0,3…1 м; r 0 = 0,019995…0,0493 м;

Ω = 100…1800 с^—1; δ = 0,05 · 10^—3…0,07 · 10^—3; К = 0,00052…0,0000022;

P_g = 0,2МПа; а = 0,1; L' = 35,33^38,1 Н/м²; М = 0,16^25,6.

Машиностроение и машиноведение

По результатам численных расчетов построены графики, приведенные на рис. 2–5.

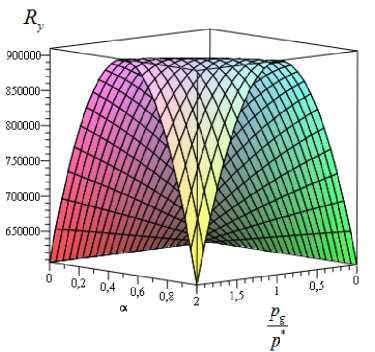
Рис. 2. Зависимость компонента поддерживающей силы ( R_y ) от параметра α,

характеризующего зависимость вязкости от давления, и от ^pg , характеризующего давление на торцах интервала, при K = 0 *

p

• Fig. 2.    Dependence of supporting force component ( R_y ) on parameter α which characterizes pressure-viscosity ratio,

p and on  g* describing pressure at the interval ends at K = 0

p ^*

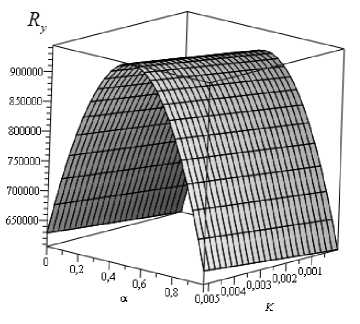
Рис. 3. Зависимость компонентов поддерживающей силы ( R_y ) от параметра α, характеризующего зависимость вязкости от давления, и от К , обусловленного расплавом и скоростью диссипации энергии

• Fig. 3.    Dependence of supporting force components ( R_y ) on parameter α which characterizes pressure-viscosity ratio,

  
  

  and on K caused by melt and energy dissipation rate

  

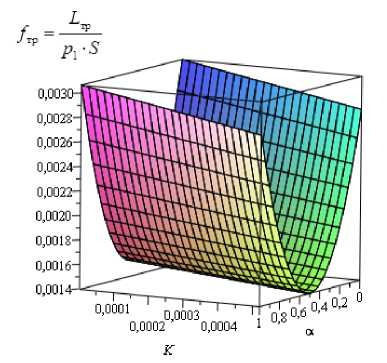
  Рис. 4. Зависимость коэффициента силы трения от параметра К , обусловленного расплавом и скоростью диссипации энергии,

  
  

  и от α, характеризующего зависимость вязкости от давления

  
  

• Fig. 4.    Dependence of friction force factor on parameter К which caused by melt and energy dissipation rate, and on α characterizing pressure-viscosity ratio

  

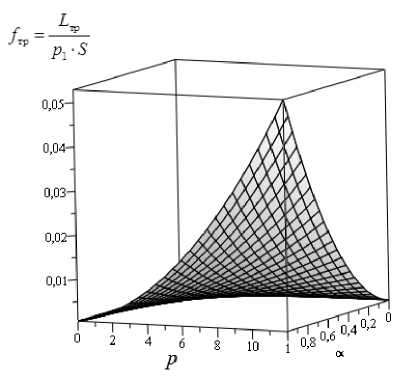
  Рис. 5. Зависимость коэффициента силы трения от параметра α, характеризующего зависимость вязкости от давления, и от гидродинамического давления р , при К = 0

  Fig. 5. Dependence of friction force factor on parameter α characterizing pressure-viscosity ratio, and on hydrodynamic pressure р at K = 0

  Выводы. Анализ полученных расчетных моделей и графиков позволяет сделать ряд выводов.

  1. Получена уточненная расчетная модель радиального подшипника скольжения, работающего в условиях гидродинамического смазывания расплавом легкоплавкого покрытия с учетом зависимости вязкости от давления.

  2. Показан значительный вклад конструктивного параметра К , обусловленного расплавом. С увеличением конструктивного параметра К коэффициент трения уменьшается на 60 %, а несущая способность увеличивается на 16 %.

  3. Зависимость коэффициента трения от конструктивного параметра К , обусловленного расплавом, близка K линейной в принятом нами приближении в пределах 0,0014–0,003.