Расчетная модель упорного подшипника с пористым покрытием на поверхности направляющей

Введение. Статья посвящена разработке расчетной модели упорного подшипника скольжения с двухслойным пористым покрытием на поверхности направляющей, работающего на электропроводящем смазочном материале. Целью работы являются: разработка и численное обоснование возможного увеличения маслоемкости, повышения несущей способности и уменьшения силы трения в результате уточнения их расчетных моделей. Это основано на формировании расчетных гидродинамических моделей упорных подшипников с учетом зависимости проницаемости пористых слоев на поверхности направляющей при установившемся течении электропроводящего жидкого смазочного материала.

Материалы и методы. Предложены новые математические модели, описывающие установившееся движение электропроводящего смазочного материала в рабочем зазоре между наклонным ползуном и направляющей с двухслойным пористым покрытием. Приведенный численный анализ основных рабочих характеристик показал, что подшипники с двухслойным пористым покрытием на поверхности направляющей, значительно повышают демпфирующие характеристики опор, несущую способность подшипника и уменьшают силу трения. Результаты исследования . На основе уравнений установившегося движения электропроводящего несжимаемого жидкого смазочного материала для «тонкого слоя» в рабочем зазоре, неразрывности и Дарси при наличии электромагнитного поля, сформирована расчетная модель упорного подшипника скольжения с учетом проницаемости пористого покрытия на поверхности направляющей. Авторами найдено точное автомодельное решение упорного подшипника с двухслойным пористым покрытием на поверхности направляющей для поля скоростей и давлений в смазочном слое и пористом покрытии, а также многопараметрические выражения для основных рабочих характеристик подшипника, учитывающих наличие электромагнитных полей, проницаемость пористых слоев и отношение толщин пористых слоев.

Обсуждение и заключения . Полученные уточненные расчетные модели позволили установить влияние ряда дополнительных факторов, а также выполнить сравнительный анализ

Introduction. The development of the design model of a thrust sliding bearing with a two-layer porous coating on the way surface running on an electrically conductive lubricant is described. The work objectives are the development and computational justification of the possible increase in oil consumption, growth of the bearing capacity, and reduction of the frictional force, due to their design models refinement. This is based on the formation of the computed hydrodynamic models of thrust bearings taking into account the dependence of the porous layers permeability on the way surface under the steady flow of the electroconductive liquid lubricant.

Materials and Methods. New mathematical models that describe a steady flow of the electrically conductive lubricant in the working gap between an inclined slider and a guide with a bilayered porous coating are proposed. The given numerical analysis of the essential performance features has shown that bearings with a two-layer porous coating on the way surface significantly increase the damping characteristics of the supports and bearing capacity of the bearing, and reduce the frictional force.

Research Results. A design model of the thrust sliding bearing is formed taking into account the porous coating permeability on the way surface. That is based on the equations of the steady flow of the electrically conductive incompressible liquid lubricant for a “thin layer” in the working gap, continuity and Darcy in the presence of an electromagnetic field. The authors have found the exact self-similar solution to a thrust bearing with a two-layer porous coating on the way surface for the field of velocities and pressures in the lubricating layer and porous coating. Besides, multiparameter expressions for the essential bearing performance with the account for the availability of electromagnetic fields, the permeability of porous layers, and the ratio of the thicknesses of porous layers, are specified.

Discussion and Conclusions. The received updated calculation models have made it possible to determine the effect of a number of additional factors, as well as to perform a comparative analysis вновь полученных результатов и уже имеющихся, что под-      of the newly obtained results and those already available which тверждает большую приближенность новой модели к реаль-      confirms the close approximation of the new model to the actual ной практике. Расчетные модели обеспечивают необходимые      practice. The theoretical models provide the necessary engineering инженерные проектировочные вычисления в достаточно ши-      design calculations in a sufficiently wide range of speeds and роком диапазоне скоростей и нагрузок для применения в ма-      loads for the application in engineering, aircraft building, instru- шиностроении, авиастроении, приборостроении и т.д.              ment making, etc.

щей.

Образец для цитирования: Мукутадзе, М. А. Расчетная мо-      For citation: M.A. Mukutadze, A. N. Garmonina, V. M.

дель упорного подшипника с пористым покрытием на по-     Prikhodko. Design model of thrust bearing with porous coating on верхности направляющей /      М. А. Мукутадзе,      the way surface. Vestnik of DSTU, 2017, vol. 17, no.3, p. 70–77.

• А. Н. Гармонина, В. М. Приходько // Вестник Дон. гос. техн.

ун-та. — 2017. — Т.17, № 3. — С. 70–77.

Введение. Одним из важных конструктивных элементов подшипников жидкостного трения является смазочная среда. В современных машинах широко используются пористые покрытия, наносимые газотермическим напылением, обладающие более высокой маслоемкостью и демпфирующей способностью. В последнее время в качестве смазочной среды используются жидкости, обладающие электропроводящими свойствами. Анализ существующих работ в данном направлении [1–10], в которых сравнивались характеристики подшипников, работающих на электропроводящих смазочных материалах с пористым покрытием на поверхности направляющей, подтвердил эффект возрастания толщины смазочной пленки по сравнению с подшипниками, работающими на обычных смазочных материалах. Результаты работ, посвященных расчету подшипников скольжения с пористым покрытием из пористых псевдосплавов, подтверждают, что в приведенных расчетах не учитывается многослойность пористых слоев и электропроводность смазочного материала.

Постановка задачи . Рассматривается ламинарное течение электропроводящего жидкого смазочного материала в рабочем зазоре упорного подшипника скольжения с наклонным вкладышем, работающего в режиме гидродинамического смазывания, с двухслойным пористым покрытием на поверхности направляющей. Предполагается, что вкладыш неподвижен, а направляющая движется в сторону сужения зазора с постоянной скоростью u^* . Вектор магнитной индукции B ' и вектор напряженности электрического поля E' направлены так, как показано на рис. 1.

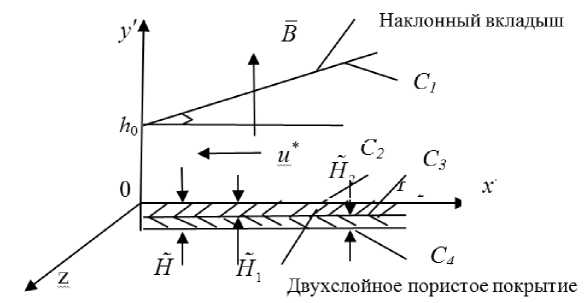
Рис. 1. Рабочая схема

Fig. 1. Functional diagram

Машиностроение и машиноведение

В декартовой системе координат уравнения ползуна C ₁ и направляющей с двухслойным пористым покрытием на ее поверхности запишем в виде:

~~

У = h o + x tg^a , у = 0 , у =- H , у =- H ! ,                                  (1)

где H ₁ — толщина пористого слоя, прилегающего к направляющей; H — толщина двухслойного пористого покрытия; h ₀ — толщина смазочной пленки в начальном сечении; α — угол наклона ползуна к оси Ох .

Предполагается, что h ₀ значительно меньше длины ползуна.

Исходные уравнения и граничные условия.

Движение электропроводящего жидкого смазочного материала в рабочем зазоре между наклонным ползуном и направляющей описывается следующим уравнением:

!2xL = ± dp_ -±о ' B^E - Bv ), zx

5y    ц dx ц где ц' — вязкость смазочного материала; p' — давление в смазочном слое; о' — электропроводность смазочного материала; B' = {0, By ,0} — вектор магнитной индукции; E' = {0,0, Ez} — вектор напряженности электрического по- ля; B — составляющая вектора магнитной индукции; Ez — составляющая вектора напряженности электрического поля. При анализе рассматриваемой задачи в качестве исходных уравнений берутся система уравнений (2), а также уравнения неразрывности и Дарси для случая «тонкого слоя».

^д 2 ^vx*   1 dp '   1                    d v,    5 v y .      d ² P   d ² P ' .

—X- =------о 'B (Ez - Bvx,), —- + —- = 0, —- +---= 0, dy'     ц ' dx'   ц '                     dx'    dy'        dx'2    dy'

где v_x , , v_y , — компоненты вектора скорости, P ' — давление в пористом слое.

При этом значения B ' = { 0, B y ,0 } и E ' = { 0,0, E z } считаются заданными и удовлетворяющими уравнениям

Максвелла:

div B ' = 0, rot E ' = 0.

Величины E' , B' и скорости течения электропроводящей жидкости таковы, что можно пренебречь влиянием потока на электрическое и магнитное поля.

Система уравнений (3) решается при следующих граничных условиях:

v x = 0 , V y = 0 при y ' = h ₀ + x ' tga ; v x = - u * , v_y . = 0 при y = 0 ;

p' ⁽⁰⁾ = p' ^{( L} ) = Pa , | P- = ⁰ при y = - H ; ^- ky | 1| y = 0 = v y l y = 0 , P 1 = ^P при y = ⁰

d y ' ²                             ц d y ^{1 y 1 y}

~ d p, k ₂ d P           ~

p = p 2 при y = - H i ; , ¹ = ; , при y = - H i . о y k 1 о y

Для описания процессов в смазочном и пористом слоях размерные величины связаны с соответствующими безразмерными следующими соотношениями:

— в смазочном слое:

*         * h                          *          μ uL

Vy, = e uu , v ^ = u v , s = — , y = h 0 y , x = Lx , p = p p , p = —, о = о , ц = ц;

L                                       h ₀

— в пористом слое:

x = Lx * , y = Ly * , P = P * P ' , k ' = k 1 , k 2 = k 2 , P 1 = P * P 1 , P 2 = P * P ₂ .                              (6)

Подставляя (5)–(6) в уравнение (3), опуская штрихи при безразмерных переменных, приходим к следующему выражению:

d ² v dp _{AT A} d и d v _n d ² P d ² P _n —у =-t + Nv - A , —+ —= 0, —*2 + —- = 0. dy dx d y d x d y d x²

о ' Bh 2                            о ' BEh 2

Здесь B = B = const, E = E = const, N =---*0- — число Гартмана, A =-----°-— величина, обусловленная ц 'u                                     ц 'u *

наличием электрического поля.

Система уравнений (7) решается при следующих граничных условиях: — в смазочном слое:

— в пористом слое:

* - y = 0

a p 2 *

d y y

• —

H = ⁰ , P 1 = P при y * = 0;

L

d P₁

d y *

y

*

~

H 1

k ₂ d P ₂

L

~ ki dy* y*=—Hi

L

P i = P 2 . H y =

Ltga   ~ k^L где n , , Mi =-h о h о

Заменяя в первом уравнении системы (7) скорость v ее максимальным значением, равным 1, точное автомодельное решение задачи, связанное с определение поля скоростей и давлений в смазочном слое, будем искать в виде:

v = It+V(x, у), u = —it+U(x,у), v(x, у)=~(E),и(x,у) = — ~ (E)h'(x), dy               dx dp C C

— N — A = ¹ + ² dx            h ²( x ) h ³( x )

т=» ft), s=hyj.

Подставляя (10) в (7) с учетом граничных условий (8)-(9), получим:

V” = C ₂, ~" = C ₁, U " + . ~ = 0, ~ = 0, ~ = 0 при £ = 1, ~ ' = 0 при Е = 0, Е = 1,

~ = 1 при £ = 0 , и

~ ⁵ P

* = M 1 *

^y = ⁰       d у

* .

у = 0

Решение задачи (10) с учетом граничных условий (11) находится непосредственным интегрированием:

~ = cveL

^^^^^^в

~

-Г+Л’+1,

V 2    )

~

т =

~

Определение гидродинамического давления

Давление в смазочном слое находим из уравнения:

dp dx

~

+ h ( x )

~

₃ ² + ( N + h ( x )

Интегрируя уравнение (13), получим

p = С (x — n x2)+ С2| x ——n x2 | + (N + A)x + pa?. V 2 ) p

Используя граничные условия p (0) = p (1) = -p a и решая уравнение с точностью до членов O ( n² ) , получим P

С2 =—(N + A )^1 +1 nj — Q^1 + 2 n x2 j

С учетом (15) для p получим следующее выражение:

p =1 n (x2 — x )(3( N + A) + 61) + pE.(16)

С учетом (16) давление фильтрующегося смазочного материала в пористых слоях будем искать в виде:

Pi(x, y *) = Pi(y *)+1 n(x 2 — x )(3( N + A) + C~1)+ par.

2 p

Подставляя (17) в уравнение Дарси для определения функции R; (у *), приходим к следующему дифференци- альному уравнению и граничным условиям:

R "( y * ) + (3( N + A ) + - 1 )n = 0 , i = 1,2; ~      ~           ~           ~          ~

R ( 0 ) = 0 R I-- ¹ 1 = R I-- ¹ 1 , R ‘ 'I-- ¹ 1 = k ² R ‘I-- ¹ 1 , R 'I--| = 0.

1121   22

V L ) I L ) I L ) k 1     I L ) V L )

Машиностроение и машиноведение

Решение задачи (18) с учетом граничных условий (19) находим непосредственным интегрированием. В результате получим:

Тогда P₁ = п С 1 + 3( N + A )

^^^^^^в

R1(y ) = n ( c , + 3( N + A )

* Z~

R ₂( y ) = n ( c , + 3( N + A )

^^^^^^B

^^^^^^в

* ^y

* 2 У

^^^^^^в

^^^^^^B

* ^y

к 2 - 2 + - 1 1

к L L I

V 1           77

H y L+

- 1 - 2 [ Ч

L ² V к₁

-17

y * ²

^^^^^^в

y

* k 2 ^-;

~ ~

V k1 L

-_х I 1

+ —11 + —

L I 2

A

7

p _a

⁺ * ^p

P ₂ = п ( С + 3( N + A )

^^^^^^в

y * ²

^^^^^^в

y

H

- —+ L

~ ~ / _

- 1 - 2 I к 2

L ² V ^к 1

^^^^^^B

1I+1

7 2

) +

7 p

Таким образом, решение задачи будет найдено

после

определения

константы С ₁. Интегрируя уравнение не-

разрывности по £ от 0 до 1

,~ ⁵ P

M —1

^d y

y * = 0

=} ^ 0

с учетом (12) и (20) для С ₁, получим следующее выражение:

I ~„

M1 ( 3( N + A ) + C1 Jl k ² -2 I к 1 L

~

+ - 1

L

^^^^^^в

С +-

Решая уравнение (22) относительно С ₁, будем иметь:

7

~

С =

~

H1

6 1 + 6 T M 1 ( N + A ) I ²

V ^к 1 ^L

~

V

+ ^- 1

L

~ ~

1 - 12 M_x I k ² H ² + ^{- 1}

¹ I k ₁ L L

,

Итак, уравнение (16) с учетом (23) можно представить в виде:

~

P = 1 л(x2 - x) 3(N + A) +

6 1 + 6 M^N + A

к ₂ H ₂

- 1 I + — I

V

к 1 L L 77

V

~ ~

1 - 12 M_x I ^ ^{- 2} + ^{- 1}

¹ I k ₁ L L

p a

+ * .

p

7

Результаты исследования и их обсуждение

Перейдем к определению основных рабочих характеристик подшипника. С учетом (12) и (24) для несущей

способности и силы трения получим следующие выражения:

ния:

W =

L тр

*                               *

P u ^L 1 1 p_Pa_ I, _ P u ^L

2 J ^P * dx ,2

h 0 0 V     p 7       h 0

= р и * L 7 ^ " (0) " h о ² it h ²( x )

^^^^^^в

v " (0) h ³⁽ x )

^^^^^^в

V

( N + A )

+

~ ~

1 + 6 Mt ( N + A J k ²- ^{— 2} + ^{— 1} I

^V 1 k 1 L L ⁷

/      А ,   ~     —

~ I к₂- 2 - I 24 M ,I -У2—У +

Ч к, L L

V V 1

I - 2

;

7 7

С 1П 1 3 I

+ — +1 - п I.

2         2 I

Для проверочных расчетов на основе полученных теоретических моделей использованы следующие их значе-

р_а = 0,08-0,101325 МПа; h ₀ = 10 - ⁷-2•10 - ⁶ м; L = 0,1256-0,1884 м; р = 0,0608 Нс/м²; и* = 1-3 м/c; A = 0,1-2; N =0,1-0,9; p = 0-16 МПа;

П = 0,3-1; k ² = 0,1-0,9; Й_г / — = 0,5-2.

k 1

Результаты численных расчетов приведены на рисунках 2-5.

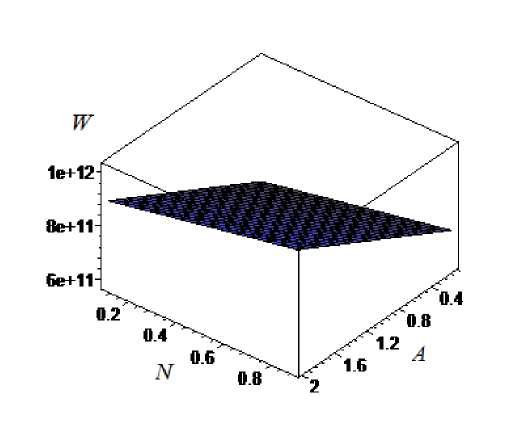
Рис. 2. График зависимости несущей способности от параметра A , обусловленного наличием электрического поля и N, числа Гартмана

Fig. 2. Dependency graph of bearing capacity on A parameter due to the presence of electric field and N, Hartmann number

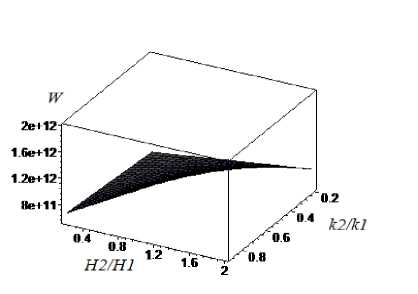
Рис. 3. График зависимости несущей способности от ( k 2 /k 1 ) отношения проницаемости пористых слоев и (H 2 /H 1 ) отношение толщины пористых слоев

Fig. 3. Dependency graph of bearing capacity on (k 2 /k 1 ) penetrability ratio of porous layers and (H 2 /H 1 ) ratio of porous layers thickness

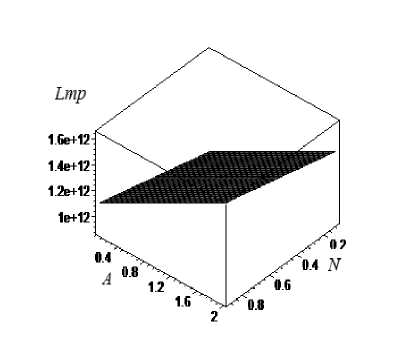
Рис. 4. График зависимости силы трения от параметра ( A), обусловленного наличием электрического поля и ( N) числа Гартмана

Fig. 4. Dependency graph of friction force on (A) parameter due to the presence of electric field and (N), Hartmann number

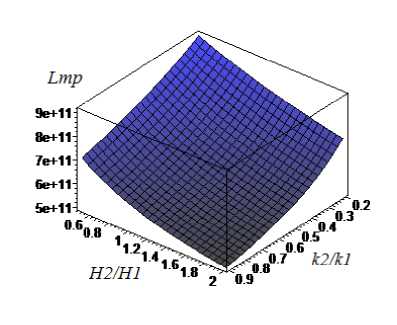
Рис. 5. График зависимости силы трения от (k2/k1) отношения проницаемости пористых слоев и (H2/H1) отношения толщины пористых слоев

Fig. 5. Dependency graph of friction force on (k 2 /k 1 ) penetrability ratio of porous layers and (H 2 /H 1 ) ratio of porous layers thickness

Выводы

Численный анализ полученных расчетных моделей и построенных на его основе графиков для упорного подшипника скольжения с двухслойным покрытием на поверхности направляющей позволил установить:

• 1.    Подшипники с двухслойным покрытием на поверхности направляющей значительно повышают демпфирующие характеристики опор и несущую способность подшипника с увеличением отношения проницаемости пористых слоев ( k 2 / k 1 ) и толщины пористых слоев ( H ₂/ H ₁), при этом сила трения существенно уменьшается.

• 2.    Существенный рост несущей способности (≈2,5 раза) наблюдается при варьировании величины числа Гартмана (N) , так же, как и величины ( A ,) обусловленной наличием электрического поля.

• 3.    С увеличением величины числа Гартмана (N) и величины (A), обусловленной наличием электрического поля, сила трения остается практически неизменной.

  Машиностроение и машиноведение