Расчетная оценка изменения фактической площади контакта при циклическом нагружении контактных пар изотропных материалов на основе моделирования параметров микрорельефа поверхности

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2022PNRPU MECHANICS BULLETIN

Эксплуатационные характеристики контактирующих деталей конструкции напрямую определяются свойствами контакта сопряженных поверхностей. При решении многих задач теплового, механического и электрического контактного взаимодействия шероховатость поверхности является ключевым фактором [1–6]. Процессы трения и изнашивания происходят именно на фактической площади контакта и зависят не только от свойств материала, но и от межконтактного давления на этой площади, поскольку величина фактического давления определяет разрушение поверхностных пленок и возникновение адгезионных связей в контакте.

Характеристиками, определяющими контактную прочность, жесткость, термо- и электросопротивление, от которых зависят силы трения и износа, являются параметры сближения поверхностей (перемещение одной поверхности касания относительно другой) и, как следствие, изменение фактической площади контакта. Именно на поверхностях фактического контакта происходят процессы адгезионного и фрикционного взаимодействий; локальное разрушение поверхностей, перенос электрических зарядов и тепловой энергии. Экспериментальные исследования с целью определения площади фактического контакта и величины сближения контактирующих поверхностей достаточно трудоемки и не дают ясного представления о реальной величине сближения поверхностей, проницаемости контакта и объеме межконтактных зазоров.

Одним из способов численного моделирования контакта является разбиение реального профиля на отдельные участки, в результате чего он формализуется и представляется как набор стержней с элементарной площадью основания и соответствующей высотой. Числовая матрица с числом элементов, равным фиксированному количеству элементарных площадок, расположенных на сопрягаемых поверхностях, является математическим аналогом такого геометрического представления [7]. При этом силы трения между смоделированными поверхностями не учитываются.

В последнее время для моделирования контакта шероховатых поверхностей используется фрактальная геометрия [8; 9]. Преимущество такого подхода заключается в том, что фрактальные параметры остаются постоянными на всех масштабах измерения шероховатости и не зависят от длины выборки.

Взаимодействие твердых тел с реальной топографией поверхности можно правильно оценить только с учетом микротопографии поверхности, которая далека от идеальной [7]. В настоящее время микрорельеф поверхности контакта определяется в основном по характеристикам профиля [10]. В общем случае характеристики микрорельефа шероховатой поверхности не совпадают с характеристиками профиля этой поверхности [11; 12]. Осуществление анализа микрорельефа поверхностей при таком подходе представляет существенные трудности. Одним из выходов из этой ситуации является создание трехмерной модели шероховатой поверхности, наиболее близкой к реальной, с использованием ее для дальнейших расчетов характеристик контакта [13–15].

Во многих известных работах для описания шероховатости поверхности используются волновые функции [17; 18], что, безусловно, сказывается на характере результатов расчета. Анализ профилограмм контактных поверхностей показывает, что профиль шероховатости поверхности носит случайный характер, который невозможно описать повторяющейся функцией. Поэтому поверхности микронеровностей, смоделированные методом с использованием волновых функций, некорректно отображают микрорельеф поверхности и, как следствие, фактическую площадь контакта между поверхностями.

Как правило, при расчетах характеристик контактного взаимодействия микрорельефа поверхностей широко используются различные аналитические методы [19; 20], позволяющие достаточно быстро определить основные характеристики контактного взаимодействия при однократном нагружении. При этом большинство из этих методов используют ряд допущений, связанных со специфическими условиями области их применения, для которых эти допущения носили оправданный характер. Учёт реального распределения выступов по высоте обычно решается с использованием кривой опорной поверхности [21] или с использованием статистических функций распределения [22–24], воспользоваться которыми в реальных задачах из-за ряда эмпирических коэффициентов достаточно затруднительно.

Если рассматривать решения задач контактного взаимодействия при циклическом нагружении, то в литературе по данному вопросу отсутствуют адекватные аналитические модели, применимые для инженерных расчетов, а представлены лишь экспериментальные данные о изменении параметров контакта. При этом стоит отметить, что неполнота приведенных экспериментальных данных, а также отсутствие описания профиля шероховатости поверхности не позволяют использовать эти данные для последующего сравнения.

От части таких допущений можно избавиться при использовании современных информационных технологий [25], позволяющих выполнять обработку значительных объемов статистической информации о параметрах рассматриваемых контактирующих поверхностей.

Современные программные и аппаратные средства цифровой обработки различных видов информации позволяют создавать цифровые двойники микрорельефа поверхности для контактных задач [26–29]. С их помощью можно создавать цифровые модели контактной пары на основе параметров рельефа поверхности, полностью учитывающие микрорельеф и повторяющие интегральные характеристики исходных данных.

1.    Моделирование взаимодействия

Цель данной работы состояла в апробации методики применения цифровых двойников микрорельефа поверхности для моделирования изменения параметров контактного взаимодействия при циклическом нагружении и определении предела качественного изменения площади реального контакта в зависимости от цикла нагружения. Далее будет рассмотрен пример использования данной методики для задач контактного взаимодействия при циклическом нагружении материалов с изотропными физическими свойствами.

В работе проанализирована модель контакта двух поверхностей с шероховатостью поверхности с Ra = 0,82 мкм и Ra = 2,07 мкм (рис. 1, 2).

После получения информации о параметрах шероховатости поверхности производится построение твердотельной модели контакта методом сплайновой интерполяции облака точек (рис. 3).

Для численного анализа контактного взаимодействия создана расчетная сеточная модель контакта, содержащая 164 952 элементов и 500 312 узлов (рис. 4).

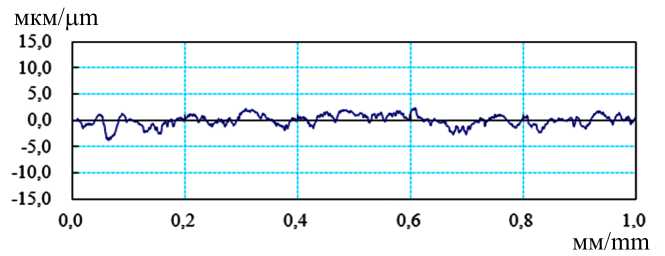
Рис. 1. Профилограмма поверхности с Ra = 0,82 мкм

Fig. 1. Profilogram of the surface with Ra = 0,82 μm

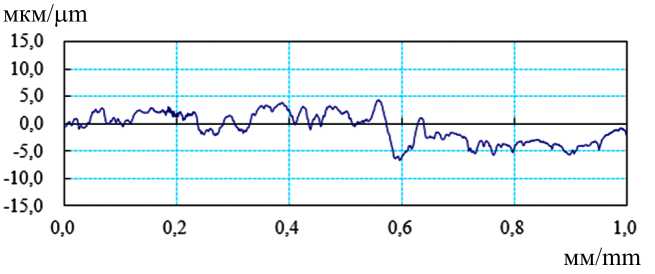
Рис. 2. Профилограмма поверхности с Ra = 2,07 мкм

Fig. 2. Profilogram of the surface with Ra = 2,07 μm

Рис. 3. Модельные контактные поверхности (верх – Ra = 2,07 мкм, низ – Ra = 0,82 мкм)

Fig. 3. Model contact surfaces (top – Ra = 2.07 μm, bottom – Ra = 0.82 μm)

Рис. 4. Сеточная модель микрорельефа поверхности

• Fig. 4.    Grid model of the surface microrelief

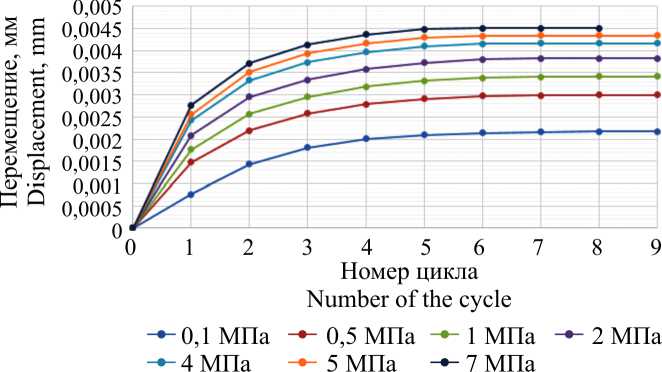
Рис. 5. Сводная диаграмма перемещений верхнего образца

• Fig. 5.    Summary diagram of displacements of the upper sample

2.    Результаты

Определение фактической площади контакта производилось по следующему алгоритму:

– задание граничных условий;

– определение величины перемещения верхнего, незафиксированного образца;

– модификация исходной геометрии по данным расчета;

– определение перемещения верхнего, незафиксированного образца и т.д.

Данный алгоритм повторялся до тех пор, пока разница в координате исследуемого образца в трех соседних расчетах становилась минимальной. Результаты величины перемещений представлены на рис. 5.

Представленные результаты позволяют сделать вывод, что перемещение исследуемого образца стабилизируется, начиная с 6-го цикла, что также иллюстрируется изменением фактической площади контакта (табл. 1, 2).

Фактическая площадь контактов, образующихся при первоначальном нагружении при разных начальных сжимающих давлениях, а также при последующих циклах, представлена на рис. 6 и 7 соответственно. Сравнение полученных изображений с результатами исследований микрорельефа поверхности с помощью оптической и растровой электронной микроскопии авторами [30; 31] наглядно свидетельствует, что картина формирования пятен контакта цифрового двойника контакта двух поверхностей, а также характер их распределения по поверхности близки к реальной картине.

Проведенные исследования циклического нагружения пар изотропных материалов на основе моделирования

Таблица 1/Table 1

Фактическая площадь контакта при циклической нагрузке, мм2

Actual contact area under cyclic load, mm2

Сжимающая нагрузка/ Contact pressure, МПа	№ цикла/Number of the cycle
	1	2	3	4	5	6	7	8	9
0,1	0,0002	0,0005	0,0010	0,0012	0,0014	0,0015	0,0016	0,0017	0,0017
0,5	0,0005	0,0018	0,0030	0,0042	0,0051	0,0054	0,0056	0,0057	0,0057
1	0,0009	0,0030	0,0053	0,0076	0,0092	0,0102	0,0107	0,0107	0,0107
2	0,0015	0,0055	0,0099	0,0136	0,0172	0,0188	0,0204	0,0204	0,0204
4	0,0025	0,0096	0,0177	0,0245	0,0289	0,0320	0,0325	0,0325	0,0325
5	0,0031	0,0125	0,0234	0,0325	0,0384	0,0407	0,0413	0,0413	0,0413
7	0,0041	0,0170	0,0308	0,0425	0,0504	0,0526	0,0526	0,0526	0,0526

Таблица 2/Table 2

Процентная доля фактической площади контакта от номинальной при циклической нагрузке

Percentage of actual contact area from nominal area under cyclic load

Сжимающая нагрузка/ Contact pressure,	№ цикла/Number of the cycle
	1	2	3	4	5	6	7	8	9
0,1	0,005	0,013	0,027	0,035	0,040	0,043	0,045	0,048	0,048
0,5	0,014	0,049	0,084	0,118	0,143	0,151	0,156	0,159	0,159
1	0,025	0,085	0,148	0,211	0,257	0,284	0,298	0,298	0,298
2	0,041	0,154	0,274	0,377	0,480	0,524	0,567	0,567	0,567
4	0,068	0,268	0,492	0,681	0,804	0,889	0,903	0,903	0,903
5	0,085	0,348	0,652	0,903	1,068	1,131	1,150	1,150	1,150
7	0,115	0,472	0,855	1,181	1,401	1,464	1,464	1,464	1,464

0,1 МПа                           2 МПа                            7 Мпа

Рис. 6. Динамика изменения фактической площади контакта на поверхности с шероховатостью Ra = 0,82 мкм при первоначальном нагружении 0,1 – 2 – 7 МПа

Fig. 6. Dynamics of change of the actual contact area on the surface with roughness Ra = 0.82 μm at the first loading of 0.1 – 2 – 7 MPa

Второй цикл Second cycle

Третий цикл Third cycle

Восьмой цикл Eighth cycle

Рис. 7. Расположение площадей фактического контакта на поверхности с шероховатостью Ra = 0,82 мкм при 2-м, 3-м и 8-м цикле нагружения при сжимающей нагрузке 7 МПа

Fig. 7. Location of actual contact areas on the surface with roughness Ra = 0.82 μm at the 2nd, 3rd and 8th cycles of loading at a contact pressure of 7 MPa параметров рельефа поверхности показывают, что деформация микровыступов прекращается в среднем на пятом цикле нагружения, и относительные перемещения модельного образца сводятся к нулю. Можно также утверждать, что поскольку задача контактного взаимо- действия двух поверхностей решалась с помощью конечно-элементного анализа, в котором решается матричное уравнение жёсткости элемента, то разработанная методика может быть распространена на широкий круг контактирующих материалов.