Расчетная оценка локального индентирования сэндвич-панели

Сэндвич-структуры изготавливают из композитных слоистых пакетов, выступающих в качестве обшивок, и легкого сотового или пенозаполни-теля. Данные компоненты играют важную роль при локальном ударном нагружении. В общем случае энергия удара рассеивается в результате локального индентирования обшивки и общего изгиба сэндвич-панели. В данной работе рассматривается первый механизм – локальное инденти-рование. С индентором взаимодействует обшивка, которая имеет возможность деформироваться в трансверсальном направлении, передавая нагрузку на заполнитель. Материалы деформируются нелинейно, прогибы в месте контакта существенно превосходят толщину обшивки, что делает задачу физически и геометрически нелинейной.

Отметим, что закон контактного взаимодействия двух изотропных упругих тел впервые был разработан Герцем [1]. Уиллис [2] исследовал контактное взаимодействие трансверсально изотропной полуплоскостью и жесткой сферой. Янг и Сан [3] выполнили ряд экспериментов по индентированию стеклоэпоксидного композита. Ву и Йен [4] представили результаты экспериментальных исследо- ваний контактного и низкоскоростного ударного нагружения слоистых пакетов при помощи жестких сферических тел. Кристофороу [5] разработал нелинейную теорию индентирования слоистых композитов. Однако эти работы слабо применимы к оценке напряженно-деформированного состояния сэндвич-панелей, ввиду того что вместо жесткой опоры имеет место легкий заполнитель.

Известно, что заполнитель в сэндвич-панелях имеет низкую прочность и достаточно высокий модуль упругости, чтобы поддерживать тонкие обшивки от потери устойчивости при сжатии. При индентировании упругое состояние заполнителя быстро исчерпывается и наступает фаза нелинейного упруго-пластического деформирования. Данной проблеме посвящено множество исследований в связи с необходимостью создания модели деформирования и разрушения сэндвич-структур при индентировании. Соден [6] представил аналитическую модель индентирования сэндвич-балок в предположении о пластическом поведении заполнителя. Шуайб и Соден [7] дополнили эту работу соответствующими экспериментальными исследованиями. При этом они использовали идеально упругопластическую модель заполнителя при сжа- тии, в которой упругая часть деформаций при ин-дентировании описывалась Винклеровской моделью основания. Хазиззян и Кантвел [9] исследовали низкоскоростной удар по сэндвич-структурам и процесс рассеяния энергии в конструкциях. Фера-боли [10] и Олссон и Макманус [11] экспериментально и численно рассмотрели сопротивляемость композитных панелей с сотовым заполнителем низкоскоростному удару. Для численных исследований авторы использовали популярные программные пакеты Abaqus [12] или LS-DYNA [13].

Можно выделить три основных подхода при аналитическом расчете последствий низкоскоростного ударного нагружения сэндвич-структур: пружинно-массовая аналогия [14, 15], использование закона сохранения энергии [9, 17–19], условные расчеты на прочность [6–7].

Большинство аналитических моделей позволяет получить значение критической силы, приводящей к разрушению обшивок сэндвич-панели при локальном трансверсальном нагружении, и лишь немногие из них подходят для определения поглощенной энергии удара вплоть до разрушения обшивок панели [20] – это связано с существенной физической и геометрической нелинейностью задачи. При этом такие модели требуют большого экспериментального материала для идентификации параметров.

В данной работе экспериментально и аналитически рассмотрен случай квазистатического ин-дентирования сэндвич-панели при помощи жест- кого сферического индентора. Разработанная аналитическая модель подходит для оценки энергии, поглощенной сэндвич-панелью вплоть до разрушения обшивки.

• 2.    Расчетная часть2.1.    Допущения

При выводе аналитических выражений для определения величины прогиба и соответствующей ему контактной силы при индентировании сэндвич-панели, лежащей на жестком основании, использовано пять основных допущений:

• 1)    нагрузка от индентора прилагается в точке;

• 2)    тонкая обшивка является упругой ортотропной мембраной (нулевая трансверсальная сдвиговая и изгибная жесткости);

• 3)    сотовый заполнитель при трансверсальном сжатии представляет собой жесткопластический материал, обеспечивающий равномерную реакцию на нижнюю поверхность вмятины;

• 4)    поверхность обшивки под индентором имеет форму пирамиды с ромбовидным основанием;

• 5)    вне зоны индентирования обшивка остается плоской и ненапряженной. Данные допущения графически проиллюстрированы на рис. 1.

• 2.2.    Анализ

Пирамидальная форма деформированной поверхности обшивки показана на рис. 1, где x и y – главные оси ортотропной симметрии слоистого пакета. На рис. 1, а показана равномерная вертикальная реакция заполнителя на воздействие об-

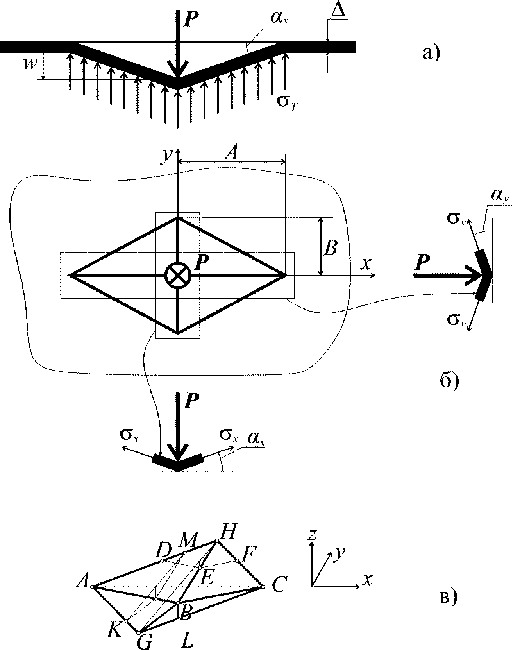
Рис. 1. Упрощенная форма поверхности деформированной обшивки в соответствии с принятыми допущениями

шивки в зоне вмятины. На рис. 1, в показана трехмерная картина перемещений обшивки в зоне ин-дентирования: линия AC переходит в ABC , линия DF – в DEF . В результате того, что треугольник ABC пропорционален треугольнику DEF , деформация в направлении оси x ( в _x ) постоянна внутри зоны нагружения. То же самое относится к оси y : линия GH становится линией GBH , KM переходит в KLM . Деформация вдоль оси у ( в _у ) также постоянна внутри деформированной области обшивки. Это позволяет далее использовать для определения напряжений в обшивке закон Гука, а для вычисления деформаций – простые геометрические построения.

В соответствии с принятыми допущениями могут быть сформированы геометрические и физические условия совместности деформаций:

• I    2~                 I Г

ww в x = ^+ A2 — 1; в у = f+ ^2 — 1;         (1)

ww tgа, =  ; tgау = -;

AB с x = QiiB x+Q12в у; су = Q12 в у + Q22 в у.

Здесь сx , су - нормальные напряжения в дефор- мированной зоне обшивки; Qij – компоненты матрицы закона ортотропной упругости Гука. В соответствии с рис. 1, б могут быть записаны уравнения равновесия (3) для всей деформированной обшивки и полос малой ширины с ориентацией направлений вырезки по осям x, y

P = 2 AB с _т ;

P = 4 а _xB A sin а _x ;                         (3)

P = 4 с _у А A sin а _у .

Система уравнений (1)–(3) позволяет найти размеры ( A , B ), глубину индентирования ( w ), и энергию ( W ) для деформированной поверхности при известной величине силы P . Очевидно, что также должны быть известны толщина обшивки ( A ), условный предел текучести заполнителя ( с _т ) и компоненты матрицы упругости материала обшивки Q ( Q 11 , Q 12 и Q 22 ).

Если глубина индентирования много меньше поперечных размеров ( w ^ А , B ), формулы могут быть дополнительно упрощены:

w = ( Pjk ) ² 3 ; р = kw ³²; W = 0,6 kw ⁵²;

k = 2 с т A[ ( Q_nQ 22 ) 12 + Q 12 ]

\ 2с т ( Q 22 / Q 11 ) ¹⁴’

P

V 2 с т ( Q_n/Q 22 ) ^V4.

Для квазистатического индентирования сэн-двич-панели в испытательной машине должен использоваться индентор в форме шара радиусом R ( R ^ А , B ). В этом случае закон P = kw ^1,5 будет справедлив вплоть до разрушения обшивки под индентором.

Для прогнозирования величины критической силы P^* , соответствующей разрушению обшивки, используется ряд дополнительных упрощающих допущений:

• 1)    под индентором несущую функцию выполняют только волокна композита;

• 2)    реальная эллиптическая площадь контакта заменяется соответствующей прямоугольной;

• 3)    для единичного волокна справедлив хрупкий механизм разрушения, но диаграмма «напряжение–деформация» при жестком нагружении слоя (миллиарды волокон) может иметь возрастающий и спадающий нелинейные участки.

В связи с этим разрушающая нагрузка может быть найдена из так называемого «предельного анализа», при котором локальное нагружение является жестким, т. е. управляемым величиной прогиба процессом деформирования (рис. 2). Для каждого значения прогиба w может быть посчитана соответствующая величина силы P ( w ) . Тогда можно записать выражение max P ( w ) = P^*.

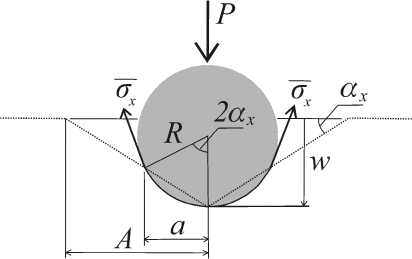
Рис. 2. Равновесие индентора на обшивке

Обшивка, находящаяся непосредственно под индентором, работает как показано на рис. 2. Обшивка меняет плоскую форму (пунктирная линия) на искривленную, при этом в поперечном разрезе она принимает вид дуги окружности с углом 2 а _x . В этом случае уравнение равновесия индентора должно быть записано в форме:

• a = R sin 2 а _x ^ 2 Rw/A ;

• b = R sin 2 а _у ^ 2 Rw/B ;                   (5)

• ^{8 R A} w ² ( ^с x ^+с у ) ''^                                                .

AB

Используя выражения (4) и (5) получим оценку разрушающей нагрузки P^* :

*     ( ^с т ^A ) ¹² [ max ( ^с x ^+с у ) ^R ]^3/2

P = 16---г¹—h—^yJ-^J—.    (6)

( Q 11 Q 22 ) ¹² + Q 12

Для определения max ( с _х + с y ) в выражении (6) сделаем следующее допущение для деформаций 8 в зоне контакта с индентором - они изменяются пропорционально, так же как и в локальной зоне окружающего материала, имеющего пирамидальную форму прогиба. Это приводит к выражению:

e = 8х/8у = 8х/8y «B2/A2 =(Q22/Qn)12. (7)

Для данных условий, плоское напряженное состояние может быть охарактеризовано в соответствии с выражением

с х = Q118х + Q128у = p ( Qn + Q12 e) ;

су = Q128х + Q228у = Р ( Q12 + Q22e) ; (8) сх + су = Р [Q11 + Q12 (1 + e) + Q22e] , где p – независимый параметр деформации, монотонно возрастающий в процессе локального нагружения, (Г - напряжение в обшивке в месте непосредственного контакта с индентором (рис. 2).

Благодаря монотропному поведению каждого слоя можно записать следующее выражение сх + су = Р [ZМ Ei (Р)5i (cos4 Vi +

+ ( 1 + e ) cos² ф i sin² ф i + e sin⁴ ф i J , (9) где ф i является углом ориентации i -го слоя, n – количество слоев, E _i ^s ( p ) – секущий модуль упругости i -го слоя вдоль армирующих волокон (функция параметра р ), 5 i - толщина слоя.

Согласно [9] обычные промышленные волокна имеют закон распределения случайной величины предела прочности, близкий к нормальному с известной медианой M и коэффициентом вариации k_V ^ 0,2. В этом случае M ^ F /0,672. Диаграмма напряженно-деформированного состояния слоя при жестком нагружении показана на рис. 3 (сплошная линия), изменение секущего модуля в процессе деформирования показано прерывистой линией.

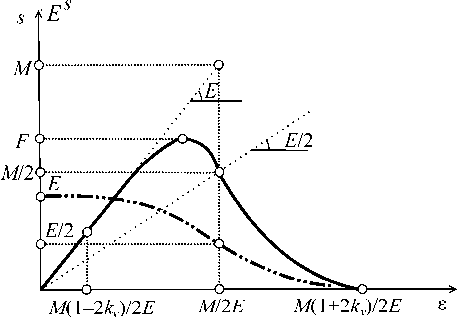
Рис. 3. Диаграмма НДС слоя при жестком нагружении

Для инженерных приложений секущий модуль может быть записан как

E i ( Р ) = E i

х

1-- Ei""^ ^х

M i k v V2n

p 0 e^xp I

( z- M i/ E i )² ' 2( M i k v/ E )

где Z — внутренний аргумент интегрирования.

Для удобства вычисления разрушающей нагрузки P * все выражения (5)–(10) были запрограммированы в популярном пакете MathCAD.

Например, в обшивке со сбалансированной укладкой типа [0/90]s или [+45/-45]s параметры Q12«Q11, A = B, a = b и max (сх +сy) « 2F . По- этому разрушающая нагрузка равна

P ^*

45,2

^G _T F ³ R ³

Q ₁₁ Q ₂₂

Выражение (11) показывает, что наиболее ве- сомыми множителями являются радиус индентора R и предел прочности обшивки F, т. е. увеличение радиуса в 1,5 раза приводит к увеличению разрушающей нагрузки в 1,84 раз. В процессе нагружения вплоть до разрушения обшивки, величина поглощенной энергии может быть определена согласно выражениям (4), (11)

W = 217

( с _T NF ⁵ R ⁵ ) ¹²

Q ₁₁ Q ₂₂

Отсюда следует, что увеличение радиуса на 10 % приведет к возрастанию поглощенной энергии до 27 %!

• 3.    Экспериментальная часть3.1.    Материалы

  В работе исследовали два вида сэндвич-панелей, имеющих различные типы слоистых обшивок: из однонаправленного углепластика КМУ-3Л с укладкой слоев [45/-45] s или тканевого арамидного пластика 10Т (укладка слоев [0/90]). Обе структуры имели сотовые заполнители, выполненные из пропитанной связующим бумаги типа No-mex или одного слоя стеклоткани. Длина стороны ячейки составляла 2,5 мм. Все механические характеристики получены из испытаний на INSTRON 5882 (машина для квазистатических испытаний) с использованием навесного экстензометра и программного обеспечения Bluehill2.

Обшивки имели симметричную укладку слоев. Для получения их механических характеристик, проведены испытания на квазистатическое растяжение образцов, вырезанных из сэндвич-панели. Трансверсальное равномерное сжатие было выполнено для образцов размерами 20 х 20 мм (испытание сотового заполнителя без специальной подготовки, т. е. с обшивками). Все необходимые характеристики показаны в табл. 1: предел проч-

Таблица 1

Механические характеристики исследуемых материалов

Образец	Обшивка			Заполнитель
1	Углепластик, [45/-45] 2s			Сотовый из пропитанной связующим бумаги
	F, ГПa	E , ГПa	∆ , мм	σ T , МПа
	0,90	50	1,04	0,85
2	Арамидный пластик, [0/90] (7 слоев)			Сотовый из однослойного тканевого стеклопластика
	F , ГПa	E , ГПa	∆ , мм	σ T ,МПа
	1,20	25	0,98	1,65

ности на растяжение F , модуль упругости E (или Q ), толщина обшивок Л и предел текучести заполнителя при сжатии а _т .

Диаграммы «напряжение – деформация» испытаний на равномерное сжатие сотового заполнителя из пропитанной бумаги и стеклопластика показаны на рис. 4.

Условный передел текучести заполнителя вплоть до деформации 40 % составляет ~0,85 МПа для типа (1) и ~1,65 МПа для типа (2). Данная характеристика соответствует среднему значению напряжений, используемому в модели идеально упругопластического материала заполнителя.

• 3.2.    Результаты испытаний

• 4.    Обсуждение результатов

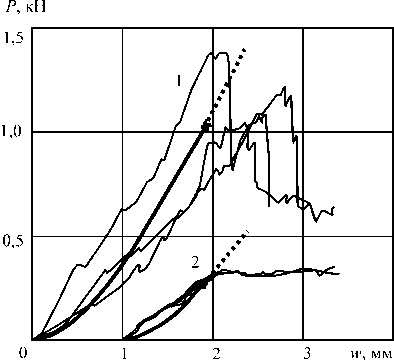
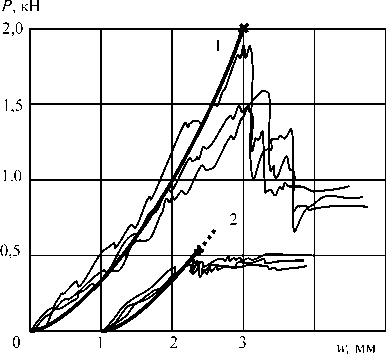
Для испытаний на индентирование использовали металлические сферы радиусом 5; 7,9 и 30 мм, скорость нагружения составляла 2 мм/мин. Диаграммы «нагрузка ( P ) – перемещение индентора ( w )» записывали в текстовые файлы формата *.csv и отображали при помощи MS Excel, рис. 5.

Диаграммы испытаний на локальное квази-статическое индентирование показаны на рис. 5 тонкими сплошными линиями. Толстые сплошные линии на рис. 5 – результаты расчета с использованием разработанной теории, выражение (4), крестиком показаны значения расчетной критической нагрузки для сэндвич-панелей, выражение (11).

Сравнение экспериментальных и расчетных результатов поглощенной энергии вплоть до разрушения обшивки представлены в табл. 2.

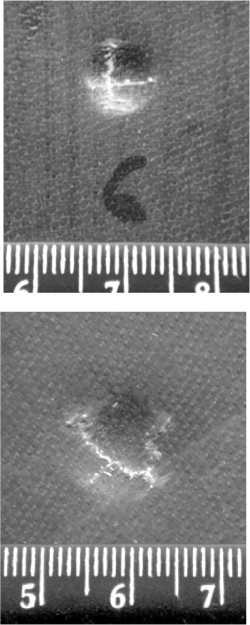
Из рис. 6 видно, что трещины в обшивке расположены непосредственно в зоне взаимодействия с индентором, причем длина трещины соответствует размеру зоны контакта (а, б), выражения 5, 6. При помощи индентора радиусом 30 мм обшивку разрушить не удалось.

Теория, предложенная в данной работе, хорошо согласуется с экспериментальными данными по локальному индентированию панелей с тонкими обшивками при помощи сферических инденторов. Исключением является начальный этап нагружения в особенности для инденторов малого радиуса и обшивок из стеклопластика. Данная особенность вызвана тем, что, во-первых, обшивка имеет определенную изгибную жесткость и не является идеальной мембраной, которая имеет участок упругой работы вплоть до начала расслоения. Во-вторых, диаграмма сжатия заполнителя не полностью соответствует определению идеально упругопластического тела. Более того, сотовый заполнитель в отличие от пены не является сплошным материалом, и зона начала инден-тирования может располагаться как внутри ячейки сотового заполнителя, так и на ее границе. Это является причиной различия начальных участков экспериментальных диаграмм индентирования. Однако разработанная методика вполне подходит для оценки энергии, поглощенной сэндвич-панелью до разрушения обшивки, так как дает

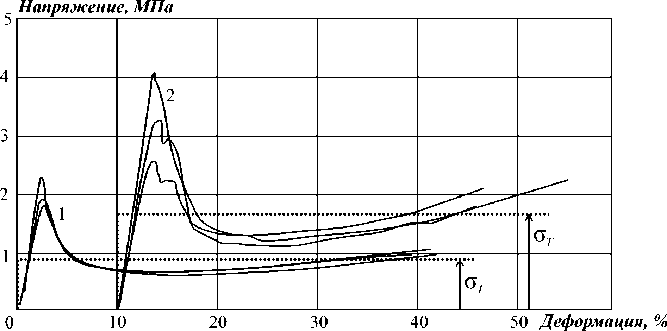
Рис. 4. Диаграммы «напряжение – деформация» испытаний на равномерное сжатие сотового заполнителя двух различных типов

а)

Рис. 5. Диаграммы индентирования, R = 5 мм (а), R = 7,9 мм (б): 1 – образец 1-го типа (стеклопластиковая обшивка);

2 – образец 2-го типа (арамидная пластиковая обшивка)

б)

Поглощенная энергия

Таблица 2

Тип образца	Радиус индентора	Энергия по результатам эксперимента, Дж	Энергия по результатам расчета, Дж	Ошибка, %
1	5	0,12±0,02	0,074	–38,3
	7,9	0,305±0,02	0,232	–23,9
2	5	1,05±0,15	0,821	–21,8
	7,9	2,42±0,14	2,58	+6,6

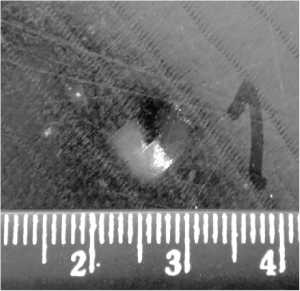
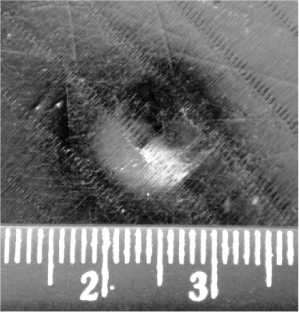
Рис. 6. Разрушение обшивки в результате индентирования: а – R = 5 мм, б – R = 7,9 мм

б)

а)

оценку в запас, т. е. нижнюю границу ее возможных значений.

Для предсказания остаточной прочности сэн-двич-панели при действии нагрузок в ее плоскости, реальная вмятина может рассматриваться как отверстие, а не трещина, так как разрушенная обшивка остается искривленной индентором и имеет жесткость, близкую к нулю.

Заключение

Упрощение реальной гладкой формы деформированной поверхности ортотропной обшивки сэндвич-панели кусочно-линейной поверхностью в зоне локального трансверсального нагружения дало возможность получить расчетные соотношения, позволяющие оценить напряженно-деформированное состояние и прочность панели при ин-дентировании на значительную глубину. Данные соотношения могут быть полезны для предварительных расчетов при проектировании конструкций. Очевидно, что разработанная теория будет также справедлива для сэндвич-панелей с пено-заполнителем.

Работа выполнялась при финансовой поддержке Минобрнауки РФ в рамках проекта «Создание высокотехнологичного производства модельного ряда инновационных энергосберегающих трамвайных вагонов модульной конструкции для развития городских пассажирских транспортных систем» по договору № 02.G25.31.0108 от 14.08.2014 г.