Расчетно-экспериментальная оценка коэффициентов запаса в конструкциях с развивающейся усталостной трещиной

Обоснование формулировок и количественных значений коэффициентов запаса является одним из основных элементов системы проектных расчетов машиностроительных конструкций.

Наиболее распространенны три подхода к определению запаса прочности: метод допускаемых напряжений, метод дифференциальных коэффициентов запаса, метод предельных состояний. В этих подходах используются формальные коэффициенты запаса, не всегда учитывающие реальные резервы прочности, которые связаны со статистическим рассеянием характеристик материалов, натру -женности, дефектности, геометрии. При рассмотрении вероятностных распределений величин, определяющих прочность конструкции, возможно пересечение областей разброса текущих и критических параметров при больших коэффициентах запаса (отношениях средних значений параметров). Такие случаи рассматриваются в модели «нагрузка-прочность».

Элементы конструкций характеризуются различными предельными состояниями и условиями работы. В связи с этим запасы прочности вычисляются по различным параметрам, характеризующим степень близости к этим предельным состояниям [ 1 ].

На протяжении многих десятилетий количественные значения запасов прочности назначались в соответствии с эмпирическим или статистическим подходами.

Исторически сложившиеся при эмпирическом подходе значения коэффициентов запаса не являются научно обоснованными в полном смысле слова [2-4]. Они не вычисляются, а назначаются и утверждаются соответствующими контрольными органами. Основой для принятия решений являются экспертные оценки, накопленный опыт, анализ действующих отечественных в смежных отраслях и зарубежных норм проектирования. При этом наличие длительного опыта эксплуатации позволяет в большинстве случаев постепенно снижать коэффициенты запаса, что является общеизвестной тенденцией [5].

Впервые статистическая природа запаса прочности в нашей стране была показана Н. Ф. Хоциаловым, за рубежом М. Майером. Здесь впервые подверглась критике концепция допускаемых напряжений и коэффициентов запаса. В противовес этому было предложено использование статистических методов прочностных расчетов. Работы Н. С. Стрелецкого [6] содержат существенное развитие идей Н. Ф. Хоциалова и М. Майера. Дальнейшее развитие методов теории вероятностей в области прочности конструкций было реализовано в работах А. Р. Ржа-ницина [7], В. В. Болотина [8]. В работах С. В. Серенсена, Е. Г. Буглова [9; 10] коэффициент запаса, ранее рассматривавшийся как основная компонента при оценке прочности, является одним из параметров для оценки надежности.

В настоящее время предпринимаются попытки развития новых методических подходов к определению запасов прочности. Они направлены: 1) на разработку новых методов вычисления количественных значений коэффициента запаса, при этом физический смысл вели-чин.1 и.1 в числителе и знаменателе выражения п =А JA остается неизменным [ 11; 12]; 2) развитие представлений о величине текущего А_т [13-15] и критического .1 [15] параметров. Вместе с тем остается актуальной задача разработки алгоритма обоснования коэффициентов запаса прочности с учетом особенностей деформирования и возможных предельных состояний несущих элементов конструкций, в том числе содержащих трещиноподобные дефекты. В данной работе развиваются и конкретизируются подходы к определению коэффициентов запаса [ 1 ] на стадии роста усталостных трещин в элементах конструкций при циклическом нагружении.

Предусмотренные нормативными документами расчетные коэффициенты запаса прочности не позволяют в полной мере решить задачу предотвращения разруше ний и аварий конструкций при эксплуатации. В связи с этим актуальными являются исследования коэффициентов запаса при наличии начальных технологических дефектов и эксплуатационных повреждений с учетом прогнозируемого их развития.

Для решения задач конструкционной прочности наибольший интерес представляют не столько абсолютные текущие значения размеров трещин, скоростей их роста, параметров механики разрушения, сколько их относительные значения, характеризующие близость к предельному состоянию, выражаемую коэффициентами запаса.

Для классических коэффициентов запаса прочности по напряжениям, имеющих длительную историю развития, в процессе которого накоплен значительный опыт анализа, расчетного и экспериментального обоснования, в большинстве случаев можно указать диапазон требуемых (приемлемых) проектных значений. Фактические значения коэффициентов должны соответствовать проектным в ограниченном количестве наиболее нагруженных конструктивных зон, и превышают их, иногда значительно, в целом по конструкции.

Этого нельзя сказать о коэффициентах запаса по параметрам, связанным с наличием развивающейся трещины. Для таких коэффициентов отсутствуют не только рекомендуемые значения, но и результаты систематических исследований их соотношения с классическими коэффициентами запаса по напряжениям. Для модельных задач (пластина с краевой или центральной трещиной, цилиндрическая оболочка с трещиной, параллельной или перпендикулярной образующей) эти соотношения могут быть установлены с использованием аналитических зависимостей механики разрушения, позволяющих вычислить коэффициенты интенсивности напряжений, критический размер и скорость роста трещины при различных уровнях номинальных напряжений. Для элементов конструкций с более сложной конфигурацией необходимо проведение серии физических и вычислительных экспериментов и выполнение расчетов, учитывающих особенности кинетики роста трещин в различных конструктивных формах. При этом особый интерес представляет сравнительный анализ оценок коэффициентов запаса, полученных по экспериментальным данным и расчетным путем.

Методику оценки коэффициентов запаса в связи с кинетикой усталостных трещин рассмотрим в предположении упругого деформирования тонкостенных конструкций в пределах, обеспечивающих адекватность применения линейной упругой механики разрушения.

Рассмотрим локальную зону элемента конструкции с уровнем номинальных напряжений ст. Классический коэффициент запаса по напряжениям (на примере запаса по пределу текучести стт) определяется по формуле пт = стт /ст.

При наличии трещины длиной / с вершиной в этой локальной зоне коэффициент интенсивности напряжений, как известно, представляется выражением

К, = oJidY , где У - поправочная функция, учитывающая особенности расчетной схемы элемента конструкции.

При известном критическом значении коэффициента интенсивности напряжений Кр коэффициент запаса по этому параметру определяется формулой пк=К1с1К,=К1с1^1¥у      (1)

Учитывая, что критический размер трещины

7с =(1/тт).(^с/стК)2, коэффициент запаса по длине трещины определим как

1 л/

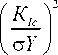
Приняв в качестве кинетического уравнения роста трещины известное уравнение v = —= С(А^Г dN V ’ для условий отнулевого цикла нагружения получим кри тическую скорость роста

Тогда коэффициент запаса по скорости роста трещины ( dl \ ( dl \ ( К, V n_v = --- / --- = —•       (⁴)

VdNydN) V.o-jTdY J

При наличии начального трещино подобно го дефекта длиной 7 максимальная долговечность элемента конструкции (число циклов нагружения, за которое длина дефекта достигнет критического значения 7) вычисляется интегрированием кинетического уравнения роста

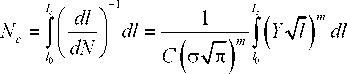
Соответственно, остаточный ресурс при любом теку щем значении длины трещины /

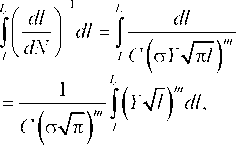
а накопленное эксплуатационное число циклов нагруже ния

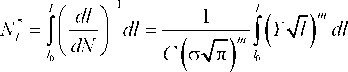
Очевидно, N_c = N* + N,.

Тогда в качестве коэффициента запаса по долговечности следует рассматривать величину стремящуюся к единице при приближении длины 7 трещины к критическому значению I.

Таким образом, на первый взгляд коэффициенты запаса по величинам, учитывающим наличие растущей трещины (п^ п_р гр, п^ однозначно связаны с уровнем номинальных напряжений s (и коэффициентом запаса по напряжениям п) посредством выражений (1, 2, 4, 5). Другими словами, зная коэффициент запаса гр, можно определить все остальные коэффициенты запаса п_к, Пр п_v, П^

Однако здесь встречается ряд затруднений, основным из которых является то, что выражение (3) (или кинетическое уравнение другого типа) основано на некоторой гипотезе о закономерности роста усталостной трещины и, соответственно, представляет собой лишь одну из возможных моделей скорости роста. Тогда расчетные коэффициенты запаса гр и n_N оказываются зависимыми от принимаемого вида кинетического уравнения и могут изменяться в широком диапазоне при неизменных технических и физических параметрах решаемой задачи. Кроме того, известные уравнения роста трещин содержат напряжения (рассчитываемые на их базе параметры механики разрушения), которые предполагаются известными (вычисляемыми). Точность оценки напряжений по длине траектории трещины в элементе конструкции достаточно сложной конфигурации, характеризующемся возможным наличием полей остаточных напряжений, невелика, что приводит к низкой точности оценок коэффициентов запаса гр и п... В связи с этим, если коэффициенты запаса и_; и п могут быть приняты по результатам соответствующих расчетов, то расчетные коэффициенты запаса гр и n_N требуется сопоставлять с таковыми, полученными по экспериментальным данным. При этом экспериментальные значения п могут быть получены только в определенном диапазоне длин трещин, а для экспериментальной оценки n_N требуется испытание образца/элемента конструкции до полного разрушения, что не всегда возможно и допустимо.

Рассмотрим получающиеся при реализации описанного предлагаемого подхода характерные результаты, полученные при циклическом нагружении образцов с развивающимися усталостными трещинами.

В качестве объекта исследования приняты три типа образцов, представляющие собой типичные конфигурации оболочечных элементов, их сочленения и местные подкрепления кольцевыми ребрами жесткости (рис. 1): образец I - цилиндрическая оболочка, подкрепленная кольцевыми ребрами жесткости (рис. 1, а), образец II - две цилиндрические оболочки с кольцевым подкреплением одной из них, сочлененные посредством конической оболочки (рис. 1, б), образец///-две цилиндрические и две конические оболочки с кольцевым подкреплением в зоне сочленения конических оболочек (рис. 1, в). В характерные зоны всех образцов внесены начальные трещиноподобные дефекты - надрезы (от 4 до 6 в каждый образец) длиной 20 мм, что соответствует эксплуатационным трещинам длиной десятки сантиметров. В качестве таких характерных зон рассматривались участки оболочек без каких-либо геометрических особенностей, а также вблизи кольцевых элементов жесткости и зон сочленения цилиндрических и конических оболочек. Трещины ориентировались в направлениях, близких к параллельному или перпендикулярному относительно образующей оболочек.

Вычисления по формулам (1,2,4,5) с варьированием текущей длины трещины 7 позволили построить расчетные зависимости коэффициентов запаса от длины трещины Пк =Д1\ И] = g(7), гр = ЦТ), nN = <7(7) (рис. 2-5). При подстановке в формулу (4) экспериментальных значений скорости роста трещин получена зависимость экспериментального коэффициента запаса п* от длины трещины п * = (/(/) (рис. 6).

Аналогичные по форме зависимости получены для всех трещин всех рассмотренных типов образцов. Количественные значения коэффициентов запаса при этом отличаются в достаточно широком диапазоне в зависимости от длины трещины (табл. 1) и определяются в основном особенностями напряженно-деформированного состояния в конструктивных зонах, содержащих трещины. Наблюдается существенное (на порядок) различие между коэффициентами запаса по скорости роста трещин, полученными расчетным путем и по экспериментальным данным, причем разница в значениях расчетных и экспериментальных коэффициентов увеличивается с ростом длины трещины. Первоначально была выдвинута гипотеза, что эта разница обусловлена несоответствием расчетных и фактических (с учетом остаточных) напряжений. Для ее проверки выполнен подбор напряжений, подставляемых в (4) таким образом, чтобы расчетные и экспериментальные значения коэффициентов запаса совпадали как минимум при конкретном значении .длины трещины. Анализ получаемых при этом результатов (рис. 7)

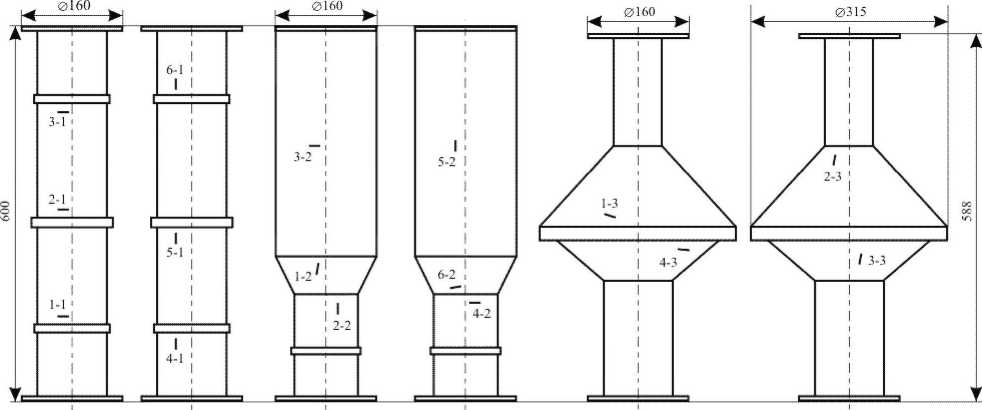
а                         б                                            в

Рис. 1. Типы экспериментальных образцов. Цифрами обозначены зоны расположения исходных трещин

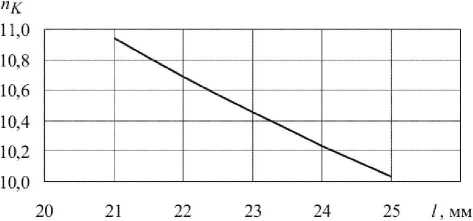
Рис. 2. Зависимость коэффициента запаса по коэффициенту интенсивности напряжений от длины развивающейся трещины для конструктивной зоны образца типа I, содержащей трещину 1-1

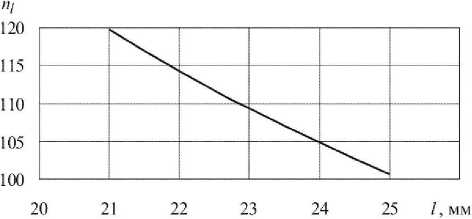
Рис. 3. Зависимость коэффициента запаса по длине развивающейся усталостной трещины от ее длины для конструктивной зоны образца типа I, содержащей трещину 1-1

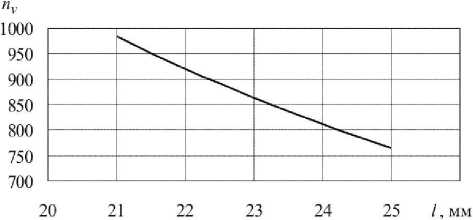
Рис. 4. Зависимость расчетного коэффициента запаса по скорости роста усталостной трещины от ее длины для конструктивной зоны образца типа I, содержащей трещину 1-1

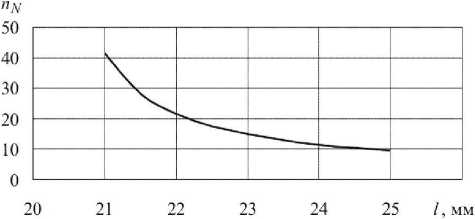
Рис. 5. Зависимость коэффициента запаса по долговечности от длины развивающейся трещины для конструктивной зоны образца типа I, содержащей трещину 1-1

показывает, что разница в расчетных и фактических напряжениях только частично объясняет различие между расчетными и экспериментальными коэффициентами запаса. Важнейшим фактором является неполная адекватность принятого кинетического уравнения для описания роста трещин при смешанных формах развития.

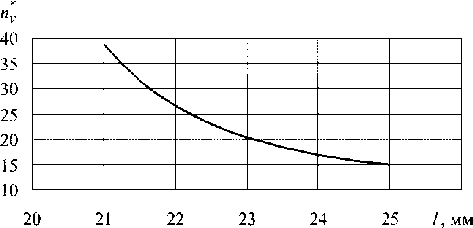
Рис. 6. Зависимость экспериментального коэффициента запаса по скорости роста усталостной трещины от ее длины для конструктивной зоны образца типа I, содержащей трещину 1-1

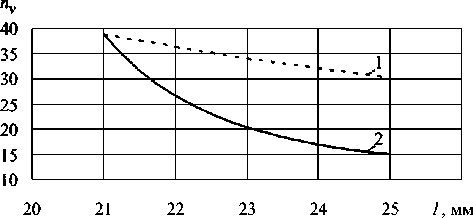
Рис. 7. Сопоставление расчетных (1) и экспериментальных (2) коэффициентов запаса по скорости роста трещины

Анализ полученных зависимостей позволяет сделать следующие основные выводы.

Количественные значения расчетных коэффициентов запаса по коэффициенту интенсивности напряжений п оказываются наименьшими, приближаются к средним по конструкции коэффициентам запаса по напряжениям и характеризуются наименьшим рассеянием. Наибольшими оказываются расчетные коэффициенты запаса по скорости роста трещины п и их рассеяние. Величины расчетных коэффициентов запаса по длине трещины и_; и долговечности n_N занимают промежуточное значение между всеми расчетными коэффициентами.

Рассмотрение количественных значений коэффициентов запаса в связи с характеристиками напряженно-деформированного состояния демонстрирует четкую тенденцию пропорционального снижения всех коэффициентов запаса с увеличением напряжений.

Расчетные оценки коэффициентов запаса по скорости роста трещин являются весьма чувствительными к принимаемым моделям кинетического уравнения роста, в связи с чем требуется тщательный анализ применимости последних с учетом особенностей напряженно-деформированного состояния конструктивных зон с трещиноподобными дефектами.

Таким образом, исследована динамика системы коэффициентов запаса с учетом кинетики роста трещин, которая должна быть положена в основу расчетно-экспериментального обоснования запасов прочности элементов конструкций с учетом возможного развития трещиноподобных дефектов.