Расчетно-экспериментальная оценка ресурса роликовых механизмов свободного хода по критерию износа

Роликовые механизмы свободного хода (МСХ) находят широкое применение в приводах различного технологического оборудования [1– 10] – металлорежущих станков, пищевых и сельскохозяйственных машин, импульсных вариаторов, автотракторных стартеров, прокатных станов и др.

Количество эксплуатируемых в нашей стране МСХ составляет десятки миллионов изделий в год. При таком значительном использовании МСХ их своевременное и правильное сервисное обслуживание является важным резервом повышения технико-экономических показателей промышленных предприятий [11].

Одним из главных факторов, определяющих ресурс роликовых МСХ, является износ рабочих элементов. Как показано в работах [3, 12– 14] износу в процессе эксплуатации подвергаются все основные рабочие элементы механизма (рис. 1) – внешняя обойма, заклинивающийся ролик, внутренняя звездочка.

Величина износа рабочих элементов и степень его влияния на работоспособность механизма различна. Наибольшее влияние на ресурс механизма оказывает износ поверхности внутренней звездочки, т.к. на этой поверхности происходит взаимодействие заклинивающегося ролика и внутренней звездочки на постоянной поверхности контакта зоне.

Износ относится к внешним повреждающим факторам, которые вызывают постепенные отказы. Зная закономерности изменения износа в период эксплуатации МСХ процесс сервисного обслуживания можно прогнозировать и управлять им. Для этого необходимо иметь диагностические модели износа роликовых МСХ.

Отсутствие знаний о закономерностях износа основных рабочих элементов роликовых МСХ не только усложняет процессы расчета и проектирования механизмов, но и в значительной мере затрудняет процесс их технического обслуживания и ремонта.

Теоретическая оценка износа представляет собой весьма трудную, в ряде случаев неразрешимую задачу. Например, в работе [3] теоретически исследовано влияние износа основных элементов МСХ на изменение угла заклинивания. Полученные выражения являются сложными для использования в инженерной прак-

где C – номинальная величина расстояния;

A h - величина износа в процессе эксплуатации.

Текущую величину угла заклинивания можно определить, как

a = a + A a ,                 (3)

тике.

где a g - номинальная величина угла закли-

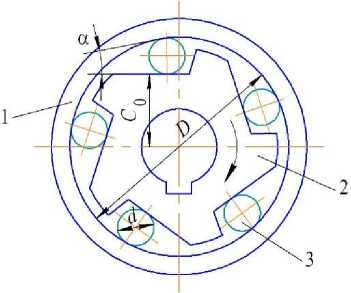
Рисунок 1 – Расчетная схема роликового МСХ: 1 – внешняя обойма; 2 – внутренняя звездочка;

3 – заклинивающийся ролик

нивания;

Aa - изменение величины угла заклинивания при износе.

Знак «минус» в формуле (2) показывает, что для при износе механизмов с внутренней звездочкой значение C всегда уменьшается, а знак «плюс» в формуле (3) показывает, что величина угла заклинивания при этом всегда увеличивается.

Преобразовав формулу (1) с учетом выражений (2) и (3) получим зависимость, показывающую влияние износа на изменение угла заклинивания

A a = arccos

Наиболее подходящей методикой получения диагностической модели износа является расчетно-экспериментальная. В этом случае данные по износу, полученные в процессе эксплуатации или экспериментальным путем, анализируются и обрабатываются с использование математических зависимостей. Как зависимый (исследуемый) фактор принимается величина износа, как независимый принимается число циклов нагружения МСХ – N .

В настоящее время нет общепризнанного подхода к нормированию допустимой величины износа в роликовых МСХ. Поэтому будем оценивать допустимую величину износа принимая во внимание известный факт, что при износе происходит изменение величины угла заклинивания.

Связь между углом заклинивания и основными геометрическими параметрами роликового МСХ с плоской рабочей поверхностью внутренней звездочки определяется зависимостью [2]

^ 2 ( C_o - A h ) + d ^

V      D - d      )

^a 0

.

При определении ресурса роликового МСХ можно принять условие, что изменение величины угла заклинивания вследствие износа не должно превышать допускаемого значения – A a <  [ A a ] .

Допуск на угол заклинивания можно принимать из опыта эксплуатации или согласно рекомендациям. Например, для механизмов приводов машин изменение угла заклинивания может составлять [ A a ] = ±1° [3], а в авиационных

приводах [ Aa ] = ±15' [15].

В реальных конструкциях роликовых МСХ номинальный угол заклинивания меняется в достаточно узком диапазоне «0 =4...8°. Сле-

2 C

----+ 1

a

arccos I

d

D

I ,

- 1

d

Текущую величину расстояния от центра механизма до плоской рабочей поверхности звездочки можно определить как

довательно, изменение угла заклинивания всего на ±1° будет составлять 12,5…25 %, что оказывает существенное влияние на работоспособность и ресурс механизма.

На рис. 2 представлены результаты расчета по формуле (4), характеризующие влияние износа на изменение угла заклинивания. Расчеты проведены для роликового МСХ по ОСТ 27-60-721-84 «Муфты обгонные роликовые» со следующими параметрами: D =100 мм; d =13 мм; C _g =36,76 мм; a_g =6°; число заклинивающихся роликов z =5.

C = C 0 "A h ,                (2)

Расчетно-экспериментальная оценка ресурса роликовых механизмов свободного хода …

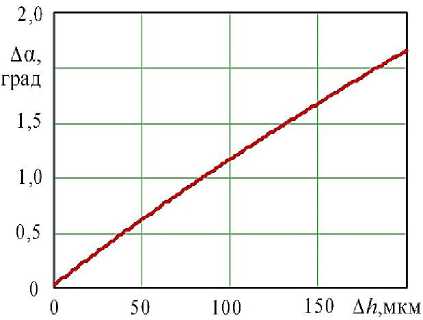
Рисунок 2 – Изменения угла заклинивания вследствие износа

Как видно из полученных результатов уже при износе звездочки A h =83 мкм изменение угла заклинивания достигает допускаемой величины [ A а ] .

Для выбора и обоснования вида диагностической модели, описывающей изменение угла заклинивания в результате износа звездочки лучше всего использовать результаты экспериментальных испытаний. Воспользуемся данными, приведенными в источнике [3]. В табл. 1 приведены параметры роликовых МСХ с тремя и пятью роликами по ОСТ 27-60-721-84 «Муфты обгонные роликовые», которые использовались в экспериментальных испытаниях. Контактные напряжения в месте взаимодействия заклинивающегося ролика и плоской поверхности звездочки составляли 1800 МПа.

Таблица 1 – Характеристики механизмов свободного хода [3]

Номер МСХ	Диаметр обоймы D , мм	Диаметр ролика d , мм	Число роликов z	Угол заклинивания а ,град
1	52	6	3	6
2	100	13	5	6

На рис. 2 представлен характер влияния числа циклов нагружения на величину износа. Следует отметить, что для механизмов с другими параметрами были получены аналогичные результаты.

Анализ приведенных результатов [16] по- казывает, что они могут быть аппроксимированы степенной зависимостью вида

A h = aN b .                 (5)

Нахождение параметров диагностической модели проведем с использованием регрессионного анализа по методики источника [17]. В качестве примера используем данные роликового МСХ №2. В расчет включим результаты первых пяти испытаний - п =5; N = 4, 6, 8, 10, 12 млн. вкл. и A h =1, 2, 10, 18, 25 мкм.

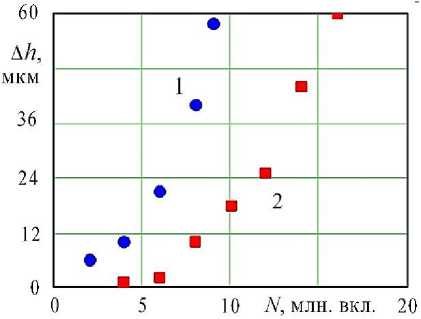
Рисунок 3 – Изменение износа от числа циклов нагружения: 1 – трехроликовый МСХ; 2 – пятироликовый МСХ

Выполним линеаризацию модели (5) используя подстановки A h' = lg A h , N' = lg N и приведем её к виду lg A h = a + b lg N или A h ' = a ' + b 'N '   (6)

В таблице 2 приведены количественные данные по расчету сомножителей, входящих в математическую модель (6).

Используя данные табл. 2 определяем коэффициенты a ' и b ' соответственно по формулам

У A h 'У ( N ' )² - У N 'Ah 'У N ' a' = — ----—--------—------—---= - 1,9823

n У ( N ’ )² - ( У N ') ²

пУ N 'Ah '- У N 'У Ah ‘ b ’ = —--------У---У----= 3,1784   (9)

n У ( N ‘ )² - ( У N ‘ ) ²

Определяем коэффициент корреляции, который показывает статистическую взаимосвязь между N' и A h ' , для модели (6) по формуле

r

_______________ п У t' s '- У t 'У s' ______________ V [ п У ( t' )² - ( У t' )²][ п У ( s ' )² - ( У s ') ²]

= 0,9799

Таблица 2 – Результаты расчетов

n	N ′	∆ h ′	( N ')2	(A h ' )2	N ′∆ h ′	N ′+∆ h ′	( N '+ A h ' )2
1	0,6020	0	0,3624	0	0	0,6020	0,3624
2	0,7781	0,3010	0,6055	0,0906	0,2342	1,0791	1,1646
3	0,9030	1,0000	0,8155	1,000	0,9030	1,9030	3,6217
4	1,0000	1,2552	1,0000	1,5757	1,2552	2,252	5,0862
5	1,07911	1,3979	1,1646	1,9542	1,5086	2,4771	6,1361
∑	4,3624	3,9542	3,9482	4,6205	3,9012	8,3167	16,3712

Величина коэффициента корреляции равная 0,9799 подтверждает, что между сомножителя модели (6) существует хорошая взаимосвязь.

Преобразуем коэффициенты a = 10 a' = 10 - ^1,9823 = 0,0104 и b = b' = 3,1784 , а затем приводим полученную линеаризованную модель (6) к окончательному виду

A h = 0,0104 N ^3,1784 (1 1)

На рис. 4 показано сравнение теоретической, полученной согласно диагностической модели (11), и экспериментальной величины износа роликового МСХ в зависимости от числа циклов нагружения. Как видно из полученных результатов наблюдается качественное и количественное совпадение результатов, величина относительной погрешности не превышает 12,7 %.

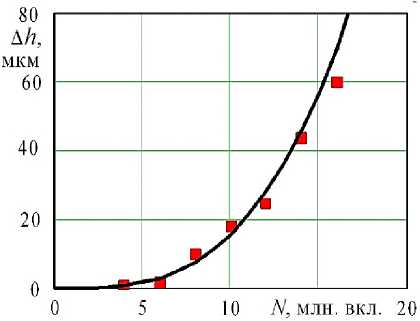
Рисунок 4 – Изменение теоретической (кривая) и экспериментальной (точки) величин износа

Оценку ресурса роликовых МСХ по критерию износа можно проводить в следующей последовательности. Сначала по диагностической модели (11) определяется величина износа ∆ h при заданном числе циклов нагружения N . После этого по формуле (4) определяется изменение величины угла заклинивания ∆ α , которая сравнивается с допускаемой [ A а ] . В табл. 3

приведены результаты оценки ресурса роликового МСХ №2 в зависимости от изменения угла заклинивания.

Таблица 3 – Число циклов нагружения и допускаемый угол заклинивания

Допускаемый угол [ Аа ]	15´	30´	1°	1,5°	2°
Число циклов N , млн. вкл.	10,5	13,5	17,0	19,5	22

Полученные диагностические модели (4) и (11) позволяют предварительно оценить ресурс роликовых МСХ и дать рекомендации по подбору режимов их эксплуатации.