Расчетно-экспериментальный анализ деформирования компенсатора температурных расширений токопровода с литой изоляцией

Литые токопроводы широко используются на предприятиях энергетики России с 2007 г: смонтировано и эксплуатируется более 40 км литых токопроводов и имеется достаточный практический опыт их применения [1]. Секции токопроводов представляют собой набор медных или алюминиевых токоведущих шин, заключенных в изолирующем материале. Характеристики поперечного сечения секций (количество и размеры шин, их расположение в объеме изоляции) варьируются в широком диапазоне и выбираются исходя из требуемых электротехнических параметров. В качестве изоляции применяют специальный полимерный компаунд с мелкозернистой структурой, получаемый методом литья и насыщенный частицами инертных материалов, обладающих мелкозернистой структурой. При сборке трассы токопровода из отдельных секций соединения шин также заливают компаундом, что обеспечивает непрерывность и высокую прочность изоляции по всей длине трассы.

Прочностные характеристики литой изоляции соответствуют нормативным требованиям и позволяют эксплуатировать токопроводы в широком диапазоне температур (от минус 60 до 40 °С). Вместе с тем, отмечены неоднократные случаи повреждения и разрушения изоляции токопроводов [2, 3], приводящие к снижению надежности энергетических сетей и опасности жизни и здоровью обслуживающего персонала. Установлено, что основная причина этих повреждений и разрушений заключается в недопустимом уровне температурных деформаций токопровода, вызванных особенностями размещения (количество и места установки) компенсаторов температурных расширений в составе трассы токопровода.

Вопросы проектирования, расчета компенсаторов температурных расширений токопро-водов крайне слабо отражены в научно-технической литературе, несмотря на то, что эти эле-– 129 – менты в значительной степени обеспечивают прочность и долговечность токопроводов с литой изоляцией в составе энергетических сетей. В связи с этим актуальны исследования, направленные на обоснование моделей деформирования компенсаторов и их использование в инженерных методах расчета трасс токопроводов.

Конструкция и принцип работы компенсатора температурных расширений

Рассмотрим одну из конструкций компенсатора температурных расширений литого то-копровода с тремя токоведущими шинами (рис. 1). Компенсатор состоит из двух изолированных блоков с выходами контактов токоведущих шин, помещенных в защитный кожух (рис. 1 а ). Электрическое и механическое соединение блоков осуществляется с помощью упругих элементов (по одному на каждую токоведущую шину) (рис. 1 б ), представляющих набор 60 медных пластин толщиной 0,2 мм, покрытых изоляцией (рис. 1 в ). Данная конструкция упругих элементов позволяет обеспечивать требуемую проводимость и при этом деформироваться с минимальной жесткостью, не влияя на деформативность трассы токопровода.

При температурном деформировании секций трассы токопровода блоки компенсатора сближаются или удаляются друг от друга с изменением зазора между ними. Основной характеристикой компенсатора при этом является допустимая величина хода H , определяющая крайнее положение блоков относительно друг друга и позволяющая нейтрализовать соответствующие температурные деформации токопровода. Анализ конструкции компенсатора показал, что относительно среднего установочного положения (рис. 2) ход блоков может изменяться как в сторону сжатия до величины – H , так и в сторону растяжения до величины + H . При этом абсолютное допускаемое значение хода H определяется растянутым состоянием, когда упру-

Рис. 1. Компенсатор температурных расширений: а – общий вид в кожухе; б – упругие элементы между блоками; в – набор пластин упругого элемента

Fig. 1. Thermal expansion compensator: a – general view in case; б – elastic elements between blocks; в – a set of plates of the elastic element

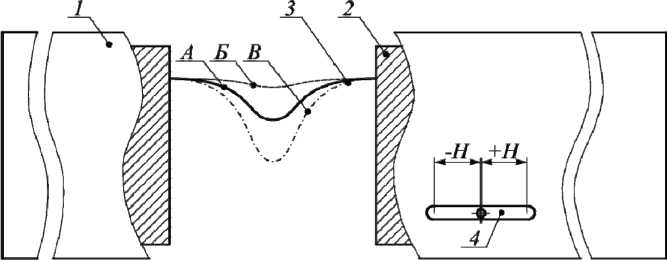
Рис. 2. Основные элементы компенсатора и их положения: 1 – кожух; 2 – блоки; 3 – упругий элемент; 4 – ограничитель хода компенсатора; А – среднее установочное положение; Б – крайнее растянутое положение; В – крайнее сжатое положение

Fig. 2. The main elements of the compensator and their positions: 1 – case; 2 – blocks; 3 – elastic element; 4 – compensator block stop; A – mean installation position; Б – maximum stretched position; В – maximum compressed position гие элементы вытягиваются полностью. Дальнейшее растяжение упругих элементов является недопустимым, так как происходит деформирование материала пластин, что значительно увеличивает жесткость компенсатора. Для недопущения данных деформаций в компенсаторе температурных расширений предусмотрен ограничитель хода, выполненный в виде паза на кожухе (рис. 2).

Таким образом, в номинальном режиме эксплуатации ход компенсатора определяется длиной ограничителя. В нештатном режиме при недостаточном количестве компенсаторов на трассе, когда суммарные температурные расширения превышают ход компенсатора, может возникнуть аварийная ситуация, приводящая к разрушению как компенсатора, так и секции вследствие дополнительных нагрузок от некомпенсированных температурных деформаций.

В связи с этим количественное описание деформирования компенсатора, определение его жесткости и допускаемого хода являются важными задачами. Данные характеристики, определяющие номинальный режим работы, должны быть положены в основу инженерных расчетов требуемого количества и условий размещения компенсаторов на трассе, в нештатном режиме – для априорного прогнозирования развития аварийных ситуаций и поверочных расчетов при научно-технической экспертизе токопроводов с литой изоляцией.

Экспериментальный анализ деформирования упругого элемента

Цель эксперимента заключалась в определении фактической жесткости и величины хода упругого элемента, описываемой диаграммой «нагрузка-удлинение». Испытательный образец был изготовлен из упругого элемента, вырезанного из компенсатора, работающего в составе трассы токопровода на Богучанской ГЭС (рис. 3 а ).

Испытание на растяжение проводилось на испытательной машине Р-50М-авто, оснащенной системой измерения/управления ASTM-Digital «Профессиональная» (рис. 3 б ), и включало две стадии:

• 1)    испытание упругого элемента в диапазоне его рабочего хода и определение жесткости компенсатора в номинальном режиме эксплуатации;

• 2)    испытание в диапазоне, превышающем рабочий ход вплоть до полного вытягивания упругого элемента.

При проведении испытания строилась диаграмма растяжения, связывающая усилие испытательной машины N и удлинение образца Δ h (рис. 4).

Рис. 3. Испытания образца упругого элемента компенсатора температурных расширений: а – образец; б – испытательная машина

• Fig. 3.    Testing of the elastic element of the thermal expansion compensator: a – sample; б – testing machine

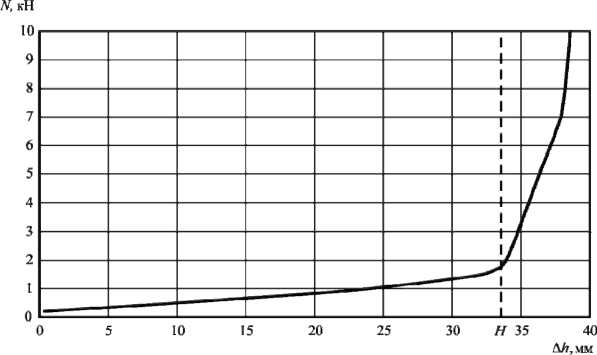
Рис. 4. Экспериментальная диаграмма растяжения упругого элемента

• Fig. 4.    Experimental tensile diagram of the elastic element

Согласно полученной диаграмме, две стадии деформирования образца характеризуются различной жесткостью, что соответствует разному углу наклона. На первой стадии деформирования упругого элемента его жесткость определяется конструктивной формой, на втором – упругостью конструкционного материала. Значение удлинения H = 33,5 мм, соответствующее точке перехода из одной стадии в другую, можно принять как допустимый ход компенсатора, при котором его жесткость минимальна.

Количественное значение жесткости упругого элемента определялось как отношение изменения нагрузки испытательной машины к удлинению образца. Значение жесткости упругого элемента в диапазоне удлинения от 0 до H составило 38,26 Н/мм. Соответственно, жесткость компенсатора с тремя токоведущими шинами, содержащего три параллельно работающих упругих элемента, увеличивается втрое и равна 114,78 Н/мм.

Численный анализ деформирования упругого элемента

При анализе напряженно-деформированного состояния трассы токопровода в целях проектирования или научно-технической экспертизы необходимо принимать во внимание наличие компенсаторов температурных расширений с учетом их переменной жесткости и ограниченности хода. При этом определение параметров компенсаторов экспериментальным путем является трудоемкой задачей и зачастую не представляется возможным. В таком случае целесообразно проводить численное моделирование для оценки деформативности компенсаторов температурных расширений. В связи с этим была поставлена задача создания численной модели компенсатора температурных расширений, позволяющей достоверно характеризовать его деформационные свойства.

При численном анализе рассматривалась конечно-элементная модель упругого элемента компенсатора температурных расширений, испытанного в ходе эксперимента. В целях выбора оптимального подхода к моделированию конечно-элементная модель была разработана в двух вариантах:

• 1)    упрощенная модель, состоящая из одной пластины и не учитывающая силу трения между пластинами. Жесткость всего упругого элемента в данном случае вычисляется умножением расчетной жесткости одной пластины на их количество. Преимущество данной модели заключается в низкой размерности и малых вычислительных затратах;

• 2)    модель с трением, состоящая из полного набора пластин. В данной модели учитывается сила трения между пластинами, что соответствует реальной конструкции упругого элемента.

В обоих вариантах упругий элемент моделировался в трехмерной постановке. Ширина одной пластины составляла 120 мм, толщина – 0,2 мм (рис. 5). Конструкционный материал – медь с модулем Юнга, равным 1,1∙105 МПа, коэффициентом Пуассона, равным 0,35, и коэффициентом трения между пластинами, равным 1. Начальная геометрия модели соответствует среднему состоянию упругого элемента (рис. 2). Для построения регулярной конечноэлементной сетки использовался конечный элемент с четырьмя узлами. Размер конечных элементов составлял 5 мм, что позволило добиться условия сеточной сходимости. Расчетная схема представлена на рис. 5.

По результатам расчета аналогично экспериментальным данным наблюдались две характерные стадии деформированного состояния упругого элемента (рис. 6). На первой стадии де-

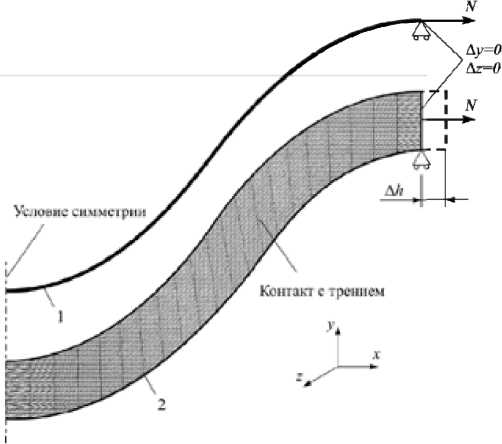
Рис. 5. Расчетная схема упругого элемента: 1 – модель с одной пластиной; 2 – модель с трением

Fig. 5. Design diagram of the elastic element: 1 – model with one plate; 2 – model with friction

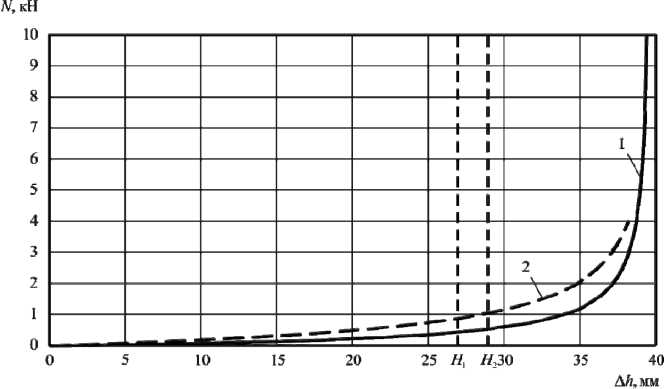
Рис. 6. Расчетные диаграммы растяжения упругого элемента: 1 – модель с одной пластиной; 2 –модель с трением

Fig. 6. Calculated tensile diagram of the elastic element: 1 – model with one plate; 2 – model with friction формирования (изменения формы) сопротивление нагрузке незначительно и характеризуется линейной зависимостью между усилием и перемещением. На второй стадии деформирования, по мере растяжения упругого элемента в прямолинейное состояние, зависимость между усилием и перемещением определяется сопротивлением материала упругого элемента, что характеризуется повышением жесткости.

По результатам обработки расчетных диаграмм растяжения были получены оценки жесткости упругого элемента компенсатора температурных расширений в пределах его допускае- – 134 –

Таблица 1. Результаты определения параметров компенсатора температурных расширений

Table 1. The results of determining the parameters of the thermal expansion compensator

Метод определения Допустимый ход компенсатора H, мм Коэффициент жесткости упругого элемента, Н/мм Коэффициент жесткости компенсатора температурных расширений, Н/мм Расчет по модели с одной пластиной 27 13,15 39,45 Расчет по модели с трением 29 34,08 102,24 Экспериментальные данные 33,5 38,26 114,78 мого хода. Допускаемый ход компенсатора H1 и H2 для соответствующего расчетного случая определялся в конце прямолинейного участка, соответствующего началу стадии деформирования материала пластин. Обобщенные значения расчетных и экспериментальных данных представлены в табл. 1.

Результаты показывают, что жесткость упругого элемента, определенная по модели с трением, выше по сравнению с расчетом по модели с одной пластиной, что обусловлено совместным деформированием пластин под действием сил трения между ними.

Сопоставление экспериментальных и расчетных результатов показывает, что экспериментально определенные коэффициент жесткости и допустимый ход компенсатора температурных расширений наилучшим образом согласуются с численным расчетом по модели с трением. Таким образом, данная модель наиболее применима для расчета компенсаторов температурных расширений.

Расчет количества компенсаторов температурных расширений для участка трассы токопровода

Как отмечалось ранее, при недостаточном количестве компенсаторов температурных расширений на трассе токопровода возникают температурные деформации и напряжения, которые потенциально приводят к возникновению разрушающих нагрузок в изоляции секций то-копровода. В связи с этим существует необходимость определения минимального количества компенсаторов температурных расширений для обеспечения прочности секций и безопасности трассы токопровода. Расчет необходимого количества компенсаторов температурных расширений может осуществляться для отдельных участков трассы токопровода с учетом особенностей ее конфигурации.

Рассмотрим прямолинейный участок трассы длиной l _line, состоящей из n прямолинейных секций, и проведем расчет количества компенсаторов k для данного участка трассы (рис. 7).

При расчете количества компенсаторов необходимо соблюдать условия сохранения длины участка токопровода и компенсации температурных расширений.

Первое условие заключается в том, что суммарная длина секций и компенсаторов должна равняться длине участка трассы:

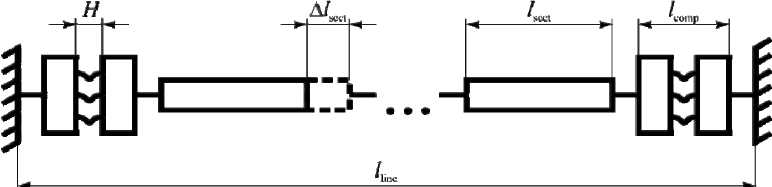
Рис. 7. Схема прямолинейного участка трассы токопровода

Fig. 7. The scheme of the linear segment of a cast resin insulated busbar system

n • l sect + k • l comp = l line ,                                                                              (1)

где n – количество секций; l – длина секции; k – количество компенсаторов; l   – длина ком- sec                                                                         comp пенсатора; lline – длина участка трассы.

Второе условие заключается в том, что суммарное изменение длины всех секций под дей ствием температуры не должно превышать суммарный допустимый ход компенсаторов:

n •Alsect ^ k • H , где ∆lsect – удлинение секции под действием температуры; H – допустимый ход компенсатора.

Из условий (1) и (2) количество компенсаторов будет определяться следующим выражением:

, А/ -L

К ______________ sect line _________

.

^{H l} sect ^{+ A l} sect ^l comp

Полученное количество компенсаторов по формуле (3) округляется в большую сторону до целого числа, чтобы гарантированно выполнялось неравенство (2).

Подставив рассчитанное значение k в условие (2), получим формулу для определения фактического количества секций на рассмотренном участке с учетом наличия компенсаторов:

n =

L - k • l line         comp

^l sect

На основе данных выражений проведем расчет количества компенсаторов на примере прямолинейного участка трассы токопровода, рассмотренного в работе [2]. Длина участка трассы составляет l line = 40 м, длина одной секции l sect = 4 м, длина компенсатора температурных расширений l _comp = 0,8 м. Исходя из экспериментальных данных, примем значение рабочего хода компенсатора H = 33,5 мм. По данным работы [2] примем значение температурного удлинения секции равным ∆ l _sect = 7,8 мм, что соответствует номинальной токовой нагрузке токопровода при эксплуатации в летний период.

Подставив исходные данные в формулу (3) и округлив в большую сторону до целого числа, получим k = 3. Далее из формулы (4) получим количество секций n = 9,4. Значение n показывает, что с учетом наличия компенсаторов на участке трассы длиной l _line = 40 м будет находиться 9 секций полной длины l sect = 4 м и одна укороченная секция длиной 0,4 l sect или

• 1,6 м. Таким образом, для компенсации температурных деформаций и безопасной эксплуатации рассмотренного участка трассы токопровода необходимо установить три компенсатора температурных расширений.

Заключение

Проведенные расчетно-экспериментальные исследования позволили определить деформационные свойства компенсатора температурных расширений. Сравнение экспериментальных и численных результатов показало их достаточное качественное и количественное соответствие, что позволяет применять численные расчеты для моделирования деформирования компенсаторов температурных расширений.

Полученные оценки допустимого хода компенсатора температурных расширений использованы при расчете необходимого количества компенсаторов для прямолинейного участка трассы токопровода.

Результаты данного исследования в совокупности являются неотъемлемой частью информационного обеспечения анализа механической прочности токопроводов [4], а рассмотренные подходы к моделированию компенсаторов температурных расширений позволяют проводить проектировочные и поверочные расчеты трасс токопроводов с литой изоляцией в целях обеспечения их безопасности и надежной эксплуатации.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края и Красноярского краевого фонда поддержки научной и научно-технической деятельности в рамках научного проекта №16-48-243022.