Расчетно-экспериментальный метод оценки усталостной прочности мпкм
Автор: Мантусова Ольга Юрьевна, Постнов Вячеслав Иванович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Механика и машиностроение
Статья в выпуске: 4-3 т.14, 2012 года.
Бесплатный доступ
В статье приводится разработка численно-аналитических методик для оценки напряженно-деформированного состояния и параметров разрушения конструкций из металлополимерных композиционных материалов, подкрепленных ребрами жесткости.
Напряженно-деформированное состояние, коэффициент интенсивности напряжений
Короткий адрес: https://sciup.org/148201293
IDR: 148201293 | УДК: 629.7.017
Текст научной статьи Расчетно-экспериментальный метод оценки усталостной прочности мпкм
определении срока службы конструкции - принципу безопасных повреждений. Этот принцип основан на предположении, что во время эксплуатации в конструкции присутствуют трещины, размер которых меньше или равен минимально обнаруживаемому средствами неразрушающего контроля.
Анализ распределения напряжений и деформаций в составном элементе конструкции с повреждением является начальным этапом для расчета его остаточной прочности и долговечности. Поэтому разработка эффективных расчетных и расчетно-экспериментальных методов определения НДС конструкций из МПКМ — весьма актуальная проблема как для задач проектирования, так при испытаниях конструкций ЛА.
Разрушение композитного материала - одна из наиболее сложных областей механики деформируемого твердого тела. Применение методов линейной механики разрушения и теории упругости к этим материалам усложнено прежде всего из-за анизотропии и неоднородности структуры КМ.
Основными методами экспериментального исследования НДС являются: тензометрический, поляризационно-оптический, рентгенографический, методы хрупких покрытий, делительных сеток, метод голографического муара.
Целью работы является разработка численно-аналитических методик для оценки напряженно-деформированного состояния и параметров разрушения авиационных конструкций из металлополимерных композиционных материалов. Полученные результаты подкрепляются экспериментальным исследованием НДС тензометрическим методом.
Исследуем предельное равновесие панели ослабленной одной прямолинейной трещиной длиной 2 l в начале координат. К пластине приклепана бесконечная периодическая система
Известия Самарского научного центра Российской академии наук, т. 14, №4(3), 2012
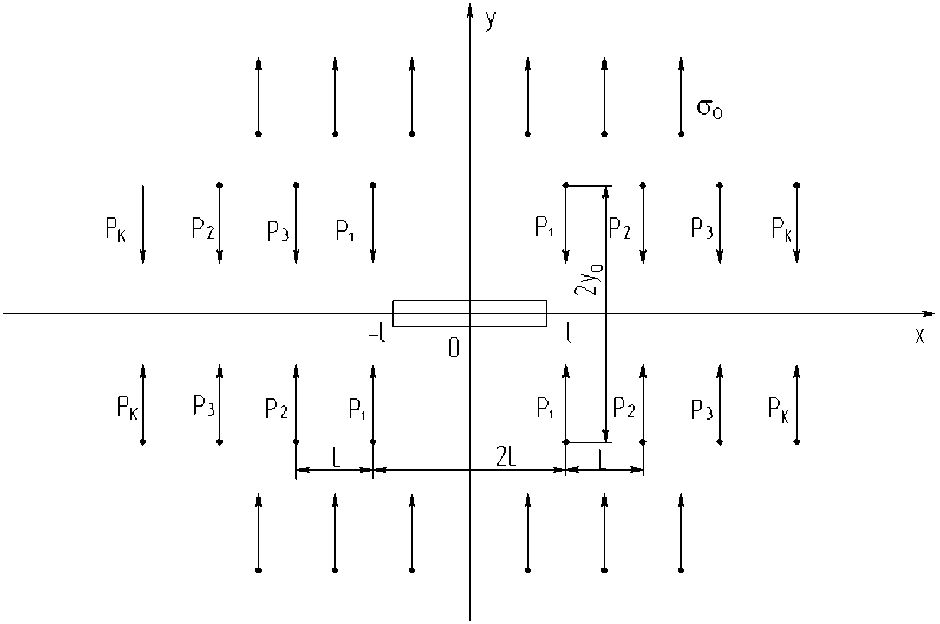
Рис. 1. Панель ослабленная одной прямолинейной трещиной длиной 2 l в начале координат
поперечных стрингеров. Действие приклепанных подкрепленных стрингеров в расчетной схеме заменим сосредоточенными силами, приложенными в местах расположения заклепок. Найдем коэффициенты интенсивности напряжений, зависимости от геометрических и физических параметров системы и приложим внешние нагрузки.
Выбор системы декартовых координат и обозначения пояснены на рис. 1.
Берега трещины свободны от внешних нагрузок. На бесконечности клепаная пластина подвергается однородному растяжению вдоль стрингеров напряжения .
Действие приклепанных подкрепляющих стрингеров в расчетной схеме заменяется сосредоточенными силами, приложенными в местах расположения заклепок. Величины сосредоточенных сил подлежат определению в результате решения задачи.
Рассматриваемая задача состоит в определении величины сил , напряженно-деформированного состояния вне трещины, а также в нахождении величины предельной внешней нагрузки , по достижению которой трещина начнет развиваться по сечению пластины.
В любой точке упругого тела напряженное состояние в случае плоской задачи определяется тремя компонентами напряжения
, которые удовлетворяют уравнениям равновесия
^i^5Z = Q
Эк Зу
Эау , £jjvy _ _
Эх Зу
Граничные условия на берегах трещины для рассматриваемой задачи имеют следующий вид: при y=0, . (2)
Согласно закону Гука величина сосредоточенной силы , действующей на каждую заклепку со стороны ребра жесткости, равна
. (3)
Здесь – модуль Юнга материала ребра жесткости, – площадь поперечного сечения реб- ра (в дальнейшем, не нарушая общности, будем считать ), – расстояние между заклепками, – взаимное смещение заклепок, равное удлинению n-го ребра.
Обозначим через r радиус заклепки. При- мем допущение о том, что взаимное упругое смещение точек в рассматриваемой задаче теории упругости равно отмеченному выше взаимному смещению заклепок Avn. Это дополнительное условие совместности позволяет эффективно отыскать решение поставленной выше задачи.
В механике разрушения важную роль играют коэффициенты интенсивности напряжений, которые отражают перераспределение напряжений в пластине вследствие наличия трещины.
Таблица 1. Результаты усталостных испытаний постоянных стопперов из МПКМ АЛОР Д16/41
|
Серия, номер образца |
Материал ПС. Вид соединения |
Кол-во циклов до разрушения, N, кцикл |
σ max , МПа |
Характер разрушения обшивки, длина трещины перед разрушением |
|
14-1 |
Алор клепка |
386,0 |
По крайнему ряду l – не определена. |
|
|
-2 -3 |
514,0 237,8 N ср =379 |
100 |
По трещине 87,8 |
|
|
16-1 -4 -5 |
Алор Клееклепка Образцы обшивки с трещиной поперечные |
N ср =326,0 |
120 |
Разрыв по крайнему ряду заклепок l =22,7 при N=158,0 Разрыв по крайнему ряду l =21,6 при N=320,0 |
Для коэффициента интенсивности напряжений КIу вершины трещины на концах будем иметь формулу
. (4)
Функция gW имеет сингулярность порядка Ѕ в окрестности .
Воспользовавшись результатами расчетов по определению коэффициентов интенсивности напряжений, представленных в работах Гаджиева В.Д. [1], коэффициент интенсивности напряжений находится соотношением
«-^("^^Т’
Г = 1
2r — 1
. (5)
Зная коэффициент интенсивности напряжений, с помощью критерия хрупкого разрушения Гриффитса-Ирвина ( ) определяем пре дельные величины внешней нагрузки , достижения которой трещина находится в подвижноравновесном состоянии.
Здесь – предельная внешняя приложенная нагрузка, – количество циклов до разрушения, – коэффициент интенсивности напряжений, – граница исследуемой области, f^.O – функция зависимости коэффициента интенсивности напряжений от начальной длины трещины и границ исследуемой области.
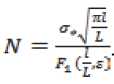
Объектами испытаний стали модельные па- нели с приклепанными стопперами трещин 140x140x1,25 мм из Алор Д16/41-2/1-0,3-Р-1,3. Характеристика нагружения: amin=10 МПа; amax= 120 МПа; частота нагружения – 10 Гц; тип испытательной машины – EUS40.
Сходимость результатов усталостной прочности панелей из МПКМ, полученных аналитическим и экспериментальным путем, составляет 98%, что говорит о возможности использования приведенной методики для расчета количества циклов до разрушения панелей при циклических нагрузках.
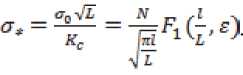
Список литературы Расчетно-экспериментальный метод оценки усталостной прочности мпкм
- Гаджиев Вахид Джалал оглы. Разрушение клепаной панели: Дисс. канд. физ.-мат. наук. Баку. 1986. 141 с.


