Расчетное исследование факельного горения мелкодисперсного лигноцеллюлозного сырья

Получение и использование экологически чистого топлива из возобновляемых лигноцеллюлозных источников выступает важной и актуальной задачей для науки и промышленности [1]. В большинстве регионов мира ведутся исследования подходящего вида топлива, включая биомассу произрастающих в регионе растений, невостребованные отходы сельского хозяйства [2], городской мусор [3], а также поиск наиболее энергетически и экологически эффективного способа его переработки.

Одним из перспективных топлив на территории России является солома пшеницы – основной отход при выращивании зерна. Этот отход практически не используется в кормлении животных и слабо востребован в других зоотехнических приложениях, например для подстилки для животных в холодных регионах страны. Вследствие слабого вовлечения соломы в сельскохозяйственный цикл она в измельчённом виде запахивается в почву при уборке зерновых или накапливается на полях и сжигается.

Наиболее перспективным способом сжигания соломы является факельное сжигание, которое при правильной организации отвечает предъявляемым требованиям как с точки зрения интенсификации, экологии, так и управления процессами. В ИТ СО РАН ведутся эксперимен-

Рис. 1. Огневой стенд ИТ СО РАН тепловой мощностью 5 МВт

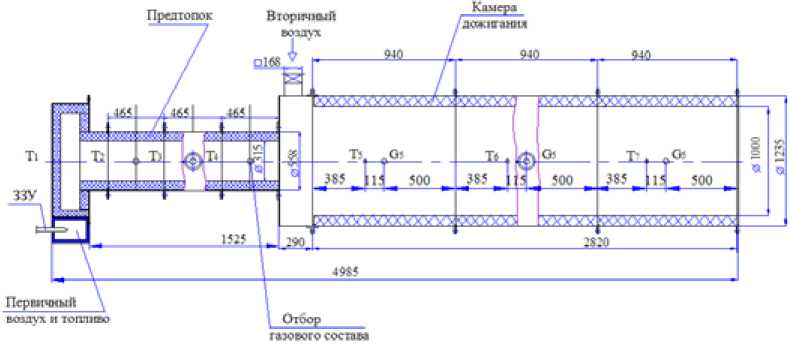
Рис. 2. Схема огневого стенда ИТ СО РАН тепловой мощностью 5 МВт тальные исследования по факельному сжиганию порошкового биотоплива, получаемого из растительного сырья (соломы пшеницы). Опыты выполняются на стенде с тепловой мощностью до 5Мвт (рис. 1). Схема топочной камеры, а также места расположения термопар показаны на рис. 2.

Стенд включает шнековый питатель дисперсной массы и систему подачи топлива в мельницу дезинтеграторного типа. Данный тип мельницы, как показали исследования, позволяет провести механоактивацию топлива с увеличением реакционных свойств топлива [4], что способствует интенсификации процесса горения и уменьшению габаритов горелочного устройства.

Новым элементом предлагаемой технологии сжигания отходов растительного сырья является комплексное использование принципов микропомола в мельнице дезинтеграторного типа с целью увеличения реакционных свойств топлива и термоподготовки топлива в предтопке при предварительном сжигании с недостатком кислорода воздуха. Если первый принцип повышает энергетические свойства топлива (интенсификацию горения), то термоподготовка топлива направлена на улучшение экологических показателей горения.

В связи со значительными затратами на проведение экспериментальных работ невозможно провести исследования для всех интересующих режимов сжигания с целью выбора наиболее оптимальных параметров горелочного устройства. Поэтому необходимо разработать математические модели, которые позволили бы получить информацию об аэродинамике, локальном и суммарном теплообмене в разрабатываемых топочно-горелочных устройствах для сжигания органического сырья.

Значительную трудность при разработке математической модели горения биомассы составляет большой разброс в химических и физических свойствах данного вещества по сравнению с углем. Несмотря на этот факт, основой для математического описания горения частиц биотоплива служат математические модели горения угольных частиц. В большинстве работ основные отличия в модели горения частицы биомассы и угля относятся к описанию движения частицы, а также ее кинетических характеристик. Предлагаемая в данной статье математическая модель горения частиц биотоплива в горелочном устройстве выступает развитием комплексной математической модели горения пылеугольного факела, описанной в работе [5]. Дополнительно в модель движения частиц был введен корректирующий фактор, учитывающий несферичную форму частицы, а также использованы кинетические характеристики процесса выхода летучих и горения коксового остатка, характерных для биомассы.

В статье рассмотрено влияние помола, который, в свою очередь, зависит от типа мельницы и количества оборотов мельничного устройства, на процесс горения в горелочном устройстве огневого стенда мощностью 5 МВт.

Математическая модель

Для описания движения потока в топочной камере была принята модель неизотермического несжимаемого многокомпонентного газа. Модель включает уравнения неразрывности, уравнения баланса количества движения, уравнение переноса концентрации компонент, уравнение переноса энергии. В общем виде уравнения сохранения для скалярной величины ф записываются

V( р v - ф) = V(Г-Vф) + Qф,      ф = {1, u, v, w, h, f, k, £}, где ф - скалярная величина; Г - эффективный коэффициент диффузионного переноса; Qф - ис-точниковый член; р - плотность, кг/м3; v - вектор скорости, м/с; u, v, w - компоненты скорости, м/с; h - удельная энтальпия, Дж/кг; к - кинетическая энергия турбулентных пульсаций, м2/с2; б - диссипация турбулентной энергии, м2/с3; f - массовая концентрация, кг/кг.

В данной статье использована модифицированная высокорейнольдсовая k- Б -модель турбулентности. Для определения пульсационных характеристик течения вблизи стенок был применен метод пристеночных функций.

Высокий температурный уровень топочной среды и поверхностей обусловливает преобладание радиационного теплообмена. Решение уравнения переноса лучистой энергии базируется на P1 приближения метода сферических гармоник. Скорость горения i-реагента, в том числе и летучих, определяется с учетом реакционной способности и концентрации горючего и окислителя, а также скорости турбулентного перемешивания топлива и окислителя. Данная модель – 627 – представляет комбинацию кинетической модели горения газовых компонент с моделью «обрыва вихря» (eddy break up model).

Для описания процессов движения угольных частиц использовали метод Лагранжа. В отличие от угольных частиц, форма которых принимается сферической, для большинства частиц биомассы (такие как древесина, солома) форма может быть несферической, а сопротивление значительно отличаться от сопротивления сферической частицы. В этом случае необходимо учитывать отклонение формы частицы от сферической с помощью введения фактора формы ( f ). Данный фактор позволяет скорректировать аэродинамическое сопротивление частицы. Фактор ( / ) определен как отношение площади поверхности эквивалентной сферической частицы к реальной площади поверхности частицы. Сопротивление, которое действует на несферическую частицу, в данной модели выражено через число Рейнольдса для частицы и фактора формы f [6]:

C D = (24 / Re)(1 + b 1 Re ^{b 2}) + [ b ₃ Re/ ( b ₄ + Re)]

b1 = exp(2.3288 - 6.4581f + 2.4486f 2)

b2 = 0.0964 + 0.5565f b3 = exp(4.9050-13.8944f + 18.4222f2 -10.2599f3) b4 = exp(1.4681 +12.258f - 20.7322f2 +15.8855f3)     , где bi, b2, b3 и b4 - функции фактора формы.

Учет турбулентности потока на движение частицы производится введением случайных флуктуаций скорости газа в уравнение движения частиц. Это так называемая stochastic separated flow (SSF) модель.

Для расчета температуры частицы с учетом конвективного и радиационного теплообмена частицы с окружающим газом использовали математическую модель с рядом эмпирических выражений, которые дали возможность скорректировать теплообмен с учетом массообменных процессов, происходящих при прогреве и горении угольной частицы [7].

Процесс горения частицы биомассы рассматривается подобно горению частицы угля и представляется в виде следующих последовательных этапов: испарение остаточной влаги из топлива, выход и горение летучих компонент и горение коксового остатка.

Испарение остаточной влаги из топлива рассчитывается из разницы концентрации водяного пара на поверхности частицы и в объеме.

Для расчета выхода летучих из частицы биомассы выбрана одностадийная, однокомпонентная модель:

1/ « л . диф . ⁺ 1/ « Л . кин .

const

«л.диф. _   ,2 , dp

^а л . кин

= К е - ^Е ВЛ / RT в . л ' e

где Vв – количество вышедших летучих, кг/кг; VT – количество летучих в исходной угольной частице кг/кг; αв.л. – скорость выхода летучих, 1/c; αл.диф. – скорость выхода в диффузионном режиме, 1/c; ал.кин, - скорость выхода летучих в кинетическом режиме, 1/c; Kв.л - предэкспонен-циальный множитель, 1/c; Eв.л – энергия активации, Дж/моль.

Горение коксового остатка является наиболее длительной стадией. В связи со сложной и не до конца изученной структурой угля и биомассы в моделях горения коксового остатка используют эмпирические данные. В условиях недостатка кислорода для полного сгорания биотоплива в объеме муфеля горелочного устройства модель горения частицы включает в себя ре- K 1                                                                   K 2                            K 3

акцию окисления углерода: C + O 2 ^ CO 2 и реакции газификации: C + н ₂ O ^ CO + н ₂ , C + CO ₂ ^ CO .

При горении коксового остатка в модели принимается изменение диаметра частицы, постоянство плотности. Для описания горения коксового остатка применяют кинетически-диффузионную модель. Изменение диаметра частицы за счет горения описано уравнением

d (d p ) = A Kc dt P _K S ’ *

КС = Ck'

Si i

'               1, k- T+T k Pi в -

Nu_ДD _i

d

ki - KKe - EK. / RT, где i=O2, CO2, H2O, pk - плотность коксового остатка, кг/м3; KSC - скорость горения углерода, кг/(м2*с); NuД -диффузионное число Нуссельта; D - коэффициент диффузии в газе, м2/с; k - константа скорости реакции, м/с; k - коэффициент реакционного газообмена, м/с; в - коэффициент массообмена между частицей и газом, м/с; Kк – предэкспоненциальный множитель, 1/c; Eк – энергия активации, Дж/моль.

Для решения уравнений сохранения для газовой фазы используют широкоизвестный метод контрольного объема, суть которого заключается в разбиении расчетной области на контрольные объемы и интегрировании исходных уравнений сохранения по каждому контрольному объему для получения конечно-разностных соотношений. Для вычисления диффузионных потоков на гранях контрольного объема применяют центрально-разностную схему, имеющую второй порядок точности. При аппроксимации конвективных членов используют схему второго порядка точности. Для решения полученной системы уравнений - метод неполной факторизации, в котором факторизованы только диагональные члены. Для связи полей давления и скорости используют SIMPLE-подобную процедуру на совмещенных сетках. При движении частиц через контрольный объем формируется источниковый член, через который учитывают обмен импульсом и энергией между газом и дисперсной фазой.

Обзор изучения кинетики процессов пиролиза и горения коксового остатка показывает большой разброс данных по значениям предэкспоненциального множителя и энергии активации данных процессов. Как показали ранее проведенные исследования кинетики механоакти-– 629 – вированного угля, значения энергии активации значительно отличаются от угля, не прошедшего активацию механическим способом. Можно предположить, что значения энергии активации частиц биотоплива также будут значительно отличаться от имеющихся в литературе данных, поэтому для проведения численного моделирования необходимо предварительное проведение экспериментальных исследований по кинетическим свойствам механоактивированных частиц биотоплива. В связи с отсутствием подобных данных в качестве кинетических констант были взяты значения соломы пшеницы из работы [8], представленные в табл. 1.

В таблице 2 представлен элементный и технический состав соломы пшеницы. В таблице 3 – расходы топлива и воздуха.

Измельчение производилось на центробежно-роликовой мельнице при 2800, 3125 и 3800 об/мин и дезинтеграторе. Данные гранулометрического анализа, проведённого при помощи стандартного набора сит, представлены на рис. 3. Видно, что с увеличением энергонапряжённости уменьшается размер частиц в продукте, что делает его более пригодным для использования в качестве мелкодисперсного топлива.

Результаты расчетов

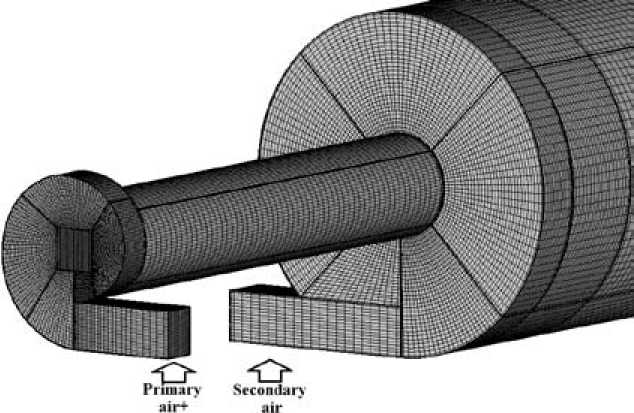
Для расчетов построения расчетной сетки и анализа результатов используется пакет программ «SigmaFlow» [9]. Расчетная сетка составляет 780 000 ячеек (рис. 4).

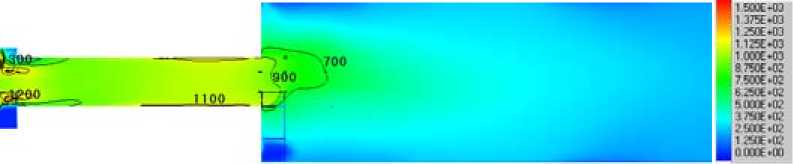
На рисунках 5а–г представлены поля температур в центральном сечении огневого стенда. Одним из основных элементов конструкции стенда, обеспечивающим стабильное воспламенение топлива, является футерованная улитка. Как показали исследования, она дает возможность воспламенить солому пшеницы в рассматриваемых вариантах, но дальнейшее развитие процесса горения в цилиндрической камере определяется свойствами топлива. Наиболее длительное воспламенение и горение наблюдаются для варианта с центробежно-роликовой мельницей при 2800

Таблица 1. Кинетические константы процесса горения соломы пшеницы [8]

	Процесс выхода летучих веществ		Горение коксового остатка
	A [1/с]	E [Дж/моль]	A [1/с]	E [Дж/моль]
Солома пшеницы	22 400	88 200	19 800 000	154 000

Таблица 2. Технический, элементный состав соломы пшеницы

Wr	Ar	V daf	Cr	Hr	Sr	Or	Nr	Qr, МДж/кг
7,3	8,92	68,28	38.2	5,56	0,31	39,0	0,71	14,28

Таблица 3. Расход биотоплива и воздуха огневого стенда

Расход биотоплива, кг/ч	Расход первичного воздуха для биотоплива, м3/ч	Расход вторичного воздуха, м3/ч
95	125	600

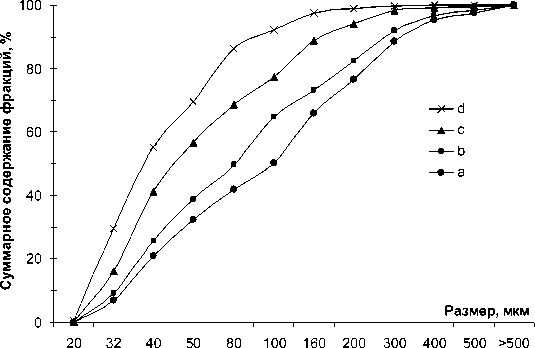
Рис. 3. Гранулометрический анализ продуктов механической активации: а–с – продукт активации на центробежно-роликовой мельнице при 2800, 3150 и 3500 об/мин соответственно; d – продукт активации на дезинтеграторе

coal dun

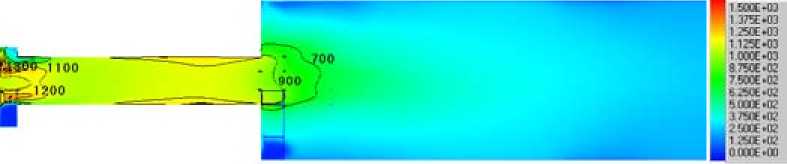
Рис. 4. Расчетная сетка камеры сгорания огневого стенда об/мин (рис. 5а). Это в первую очередь объясняется более крупным помолом частиц соломы. Похожая картина распределения температур представлена и для варианта с 3150 об/мин (рис. 5б). Значительное увеличение скорости горения биотоплива происходит при энергонапряженности мельничного устройства 3500 об/мин на центробежно-роликовой мельнице. Температуры в горелочном устройстве значительно возрастают, достигая 1300 °С в цилиндрическом канале. Максимальные температуры в горелке наблюдаются после помола биотоплива на дезинтеграторе. После помола на центробежно-роликовой мельнице при 3500 об/мин температуры немного ниже и область высоких температур смещена ближе к выходу из горелки, что свидетельствует о задержке воспламенения и горения биотоплива по сравнению с предыдущим вариантом.

а

б

в

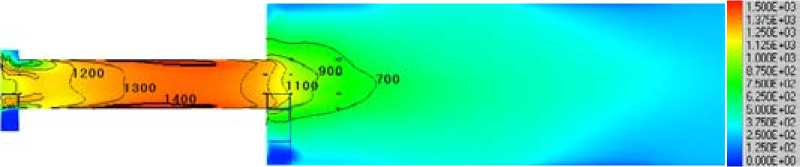
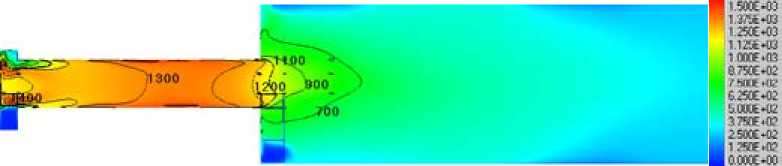
Рис. 5. Распределение температур в центральном сечении огневого стенда при измельчении соломы: а – в центробежно-роликовой мельнице при 2800 об/мин; б – 3150 об/мин; в – 3500 об/мин; г – в мельнице-дезинтеграторе

На рисунке 6 представлен график значений температур вдоль линии расположения термопар на экспериментальном стенде (рис. 2). Данные значения были получены при сжигании соломы после ее измельчения в мельнице-дезинтеграторе и расходов, представленных в табл. 3. Из данного графика можно сделать выводы о том, что полученные расчетные данные достаточно хорошо согласуются с экспериментом. Наибольшее отличие наблюдается на начальном участке факела, что может быть объяснено неучетом в модели повышения реакционной способности соломы после ее измельчения на дезинтеграторе.

На рисунке 7 показаны интегральные значения температур вдоль горелочного устройства. Самый высокий уровень температур для варианта с мельницей-+дезинтегратором. Из данного графика видно, что, несмотря на то что на начальном участке мы можем наблюдать похожие значения температур, дальнейшее развитие воспламенения топлива происходит по-разному, – 632 –

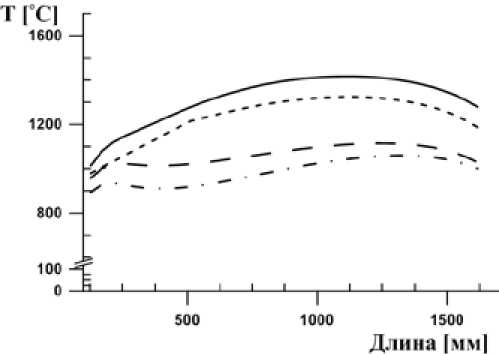
Рис. 6. Распределение температур вдоль линии расположения термопар T 2 -T 4 , °С

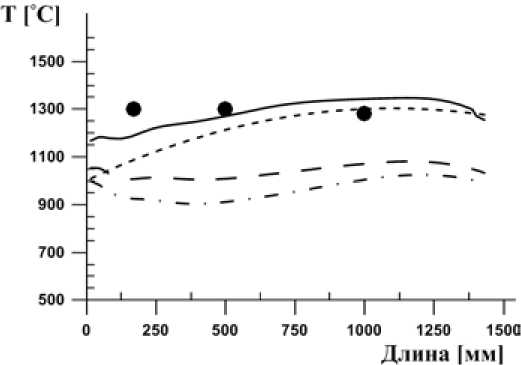
Рис. 7. Распределение интегральных температур по длине горелочного устройства, °С что объясняется отличительными характеристиками топлива после помола. Температура на выходе из горелки для варианта с помолом на центробежно-роликовой мельнице с 2800 об/мин составляет 930 °С, 3150 об/мин – 990 °С, 3500 об/мин – 1150 °С и при помоле на дезинтеграторе 1300 °С.

Распределение концентраций газовых компонент (рис. 8-10) показывает, что для варианта с дезинтегратором происходит практически полное потребление кислорода, а на выходе из горелки формируется высокореакционная смесь, которая позволяет создать условия для воспламенения и стабилизации горения в топочной камере

Выводы

С использованием разработанной математической модели выполнены расчетные исследования горения мелкодисперсного растительного сырья (соломы) на 5 МВт. Исследование влия-

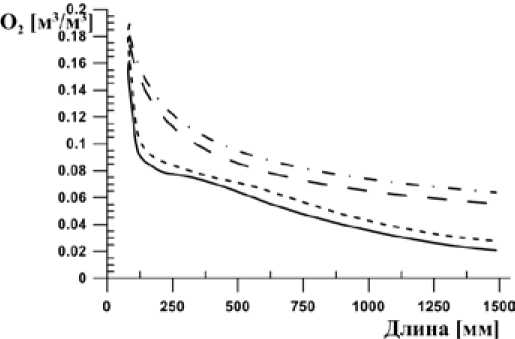
Рис. 8. Распределение концентрации кислорода по длине горелочного устройства, м3/ м3

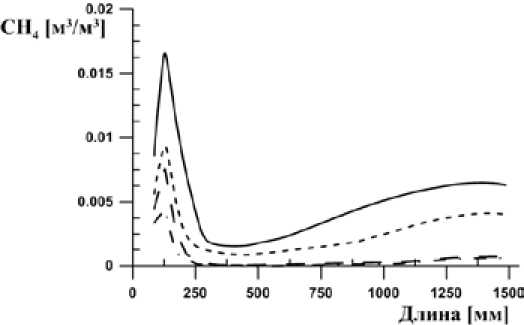
Рис. 9. Распределение концентрации летучих компонент по длине горелочного устройства, м3/ м3

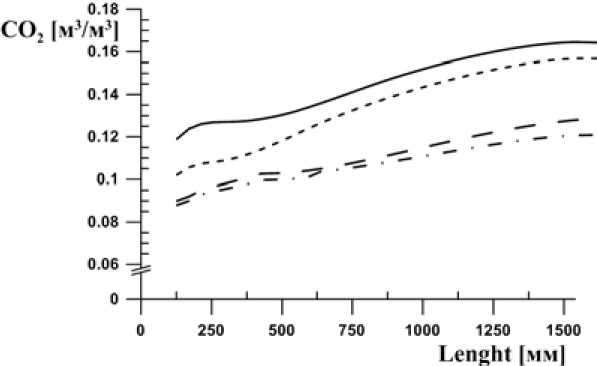
Рис. 10. Распределение концентрации CO2 по длине горелочного устройства, м3/ м3

ния степени помола на процессы воспламенения и горения в горелочном устройстве огневого стенда показало, что при размоле на центробежно-роликовой мельнице с 3500 об/мин, а также на мельнице-дезинтеграторе можно создать благоприятные условия для стабилизации факела в объеме топочной камеры. Сравнение результатов расчета с экспериментальными данными по сжиганию соломы на 5 МВт стенде ИТ СО РАН продемонстрировало удовлетворительное согласование, а также необходимость в дополнительном исследовании по определению кинетических констант горения соломы пшеницы с целью их дальнейшего использования в математической модели для оптимизации процессов сжигания биотоплива.

Работа выполнена при финансовой поддержке Государственного контракта от 29.03.2013г. № 14.516.11.0048 и СП-6672.2013.1