Расчетное исследование применения полимерных растворов на основе смеси этиленгликоль-вода для бурения многолетнемерзлых пород

Цитирование: Минаков, А.В. Расчетное исследование применения полимерных растворов на основе смеси этиленгликоль-вода для бурения многолетнемерзлых пород / А.В. Минаков, М.И. Пряжников, А.Л. Неверов, Д.В. Гузей, В.Г. Волков, В.В. Лукьянов // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(1). С. 111-127. DOI: 10.17516/1999-494X-0154

[1-7]: уменьшение температуры бурового раствора в результате его охлаждения необходимым объемом ранее заготовленной жидкости; уменьшение длительности теплового воздействия в результате повышения скорости проходки и увеличения выносной способности промывочной жидкости; уменьшение коэффициента теплоотдачи от промывочной жидкости к стенке скважины в результате создания ламинарного режима течения жидкости в кольцевом пространстве; увеличение вязкости и динамического напряжения сдвига промывочной жидкости, а также предупреждение образования вихревого движения в выемках на стенках ствола скважины; уменьшение водоотдачи, так как увеличение количества отфильтрованной жидкости в стенку скважины существенно повышает интенсивность разрушения льда.

Таким образом, для снижения скорости растепления ММП в процессе бурения необходима разработка буровых растворов с низкой температурой замерзания, теплоемкостью, теплопроводностью и набухающей способностью при сохранении высоких реологических характеристик. Анализ литературы показывает, что таким требованиям могут удовлетворять полимерные растворы на основе смеси воды и этилен- или пропиленгликолей [8-10].

В данной работе впервые проведено расчетное исследование по изучению влияния добавки этиленгликоля в полимерный буровой раствор на скорость растепления ММП в процессе бурения.

Лабораторные исследования

Сначала были проведены лабораторные исследования свойств бурового раствора. В качестве бурового раствора рассмотрена водная смесь этиленгликоля с добавлением крахмала и гаммаксана. При приготовлении растворов использовалась дистиллированная вода, которую получали очищением проточной воды при помощи монодистиллятора GFL-2004, этиленгликоль (АО «ЭКОС-1», Россия) чистый для анализа (ГОСТ 10164-75), крахмал картофельный сорт «ЭКСТРА» (ГОСТ Р53876-2010), а также ксантановый биополимер гаммаксан (ГК «Миррико», Россия).

Массовая концентрация этиленгликоля w в водной смеси варьировалась от 0 до 80 %. Массовое содержание в растворе крахмала составляло 2.0 мас. %, а гаммаксана 0.5 мас. %.

Плотность растворов рассчитывалась как сумма произведений плотности и концентрации каждого компонента, входящих в раствор (вода, этиленгликоль, крахмал и гаммаксан).

Коэффициент теплопроводности растворов измерялся с использованием метода нагретой нити. Подробное описание методики измерения коэффициента теплопроводности представлено в работе [11]. Значение коэффициента теплопроводности было определено как среднее из пяти измерений. Погрешность измерения коэффициента теплопроводности не более 3 %.

Удельная теплоемкость растворов на основе смеси этиленгликоль-вода C _p,M может быть определена с учетом объемной доли этиленгликоля φ и воды (1- φ ) следующим образом:

^P M C p,M = ^ФP EG C p,EG ^{+ (1} - ^ф ) ^p w C p,W ^{,                                        (1)}

P m = ФP EG + ( 1 - Ф ) P w ,                                                  (2)

C p,EG, Cp,W, ρEG, ρW – удельная теплоемкость и плотность этиленгликоля и воды соответственно.

Исследование реологии созданных буровых растворов проведено при помощи ротационного вискозиметра OFITE 900. Диапазон скорости сдвига ͘ γ от 0.01 до 1022 с^-1. Точность поддержания скорости вращения 0.001 об/мин. При измерении реологии использовалась методика, описанная в работе [12]. Погрешность измерения коэффициента вязкости 2 %.

Все измеренные и рассчитанные свойства представлены в табл. 1.

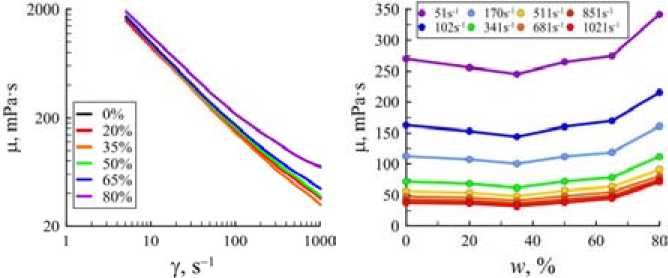
Зависимость вязкости полученных растворов от скорости сдвига и концентрации этиленгликоля приведена на рис. 1. Как видно, с увеличением скорости сдвига вязкость уменьшается для всех концентраций этиленгликоля. Таким образом, данные растворы являются псевдопластическими жидкостями. Зависимость эффективной вязкости от концентрации этиленгликоля показывает, что при низких значениях скорости сдвига вязкость раствора имеет минимум при концентрации, равной 35 мас. %. При этом снижение вязкости в минимуме не очень значительное и составляет около 15 %. При дальнейшем увеличении концентрации ЭГ вязкость раствора увеличивается. При высоких значениях скорости сдвига с увеличением концентрации ЭГ вязкость монотонно возрастает. Однако с практической точки зрения было установлено, что влияние этиленгликоля (за исключением очень высокой концентрации 80 мас. %) на эффективную вязкость полимерного раствора является незначительным.

Реология рассматриваемых растворов была описана с помощью наиболее распространенных степенной (Power-law) и бингамовской (Bingham) моделей. Полученные реологические параметры этих моделей представлены в табл. 1. Анализ поведения реологических параметров буровых растворов демонстрирует, что показатель консистенции K слабо зависит от концентрации этиленгликоля (ЭГ). Показатель степенной модели n с увеличением концентрации ЭГ незначительно увеличивается. Пластическая вязкость PV и предельные напряжения сдвига YP при концентрациях ЭГ ниже 35 мас. % незначительно снижаются по сравнению с базовым раствором. При дальнейшем повышении концентрации ЭГ эти характеристики монотонно возрастают. Однако в абсолютном выражении за исключением концентрации 80 % эти изменения

а )

б )

Рис. 1. Зависимость вязкости буровых растворов от скорости сдвига при различных концентрациях ЭГ (а) и от концентрации ЭГ при различных значениях скорости сдвига (б)

Fig. 1. Dependence of drilling fluids viscosity on shear rate at different concentrations of EG (a) and on concentration of EC at different values of shear rate (б)

Таблица 1. Плотность, реологические и теплофизические свойства буровых растворов

Table 1. Density, rheological and thermophysical properties of drilling fluids

w, % ρ, kg/m3 PV, mPa·s YP, Pa K, Pa·sn n k, W/(m·K) Cp, kJ/ (kg·K) 0 1006 30.26 11.71 4.94 0.279 0.624 4.18 20 1028 29.35 10.94 4.59 0.283 0.550 3.80 35 1045 24.23 10.98 5.29 0.242 0.495 3.52 50 1061 30.37 11.64 5.17 0.270 0.430 3.25 65 1078 37.03 11.90 4.90 0.298 0.371 2.99 80 1095 61.18 13.71 4.95 0.354 0.324 2.74 являются несущественными. Таким образом, можно утверждать, что добавка этиленгликоля вплоть до высоких концентраций (65 мас. %) не ухудшает реологических свойств полимерных растворов.

Измерения коэффициента теплопроводности k и оценки удельной теплоемкости C p буровых растворов с этиленгликолем показали значительное снижение этих характеристик (табл. 1). Так при концентрации ЭГ в растворе 65 мас. % коэффициент теплопроводности снижается на 70 %, а теплоемкость – на 40 %.

Полученные в результате лабораторных исследований данные по свойствам буровых растворов с этиленгликолем использовались в дальнейшем при численном моделировании.

Математическая модель циркуляции бурового раствора в скважине с учетом растепления ММП

Расчетному исследованию процесса растепления пород вокруг скважин посвящено большое количество работ [2, 3, 13-16]. При этом большинство расчетных исследований в данной области посвящено процессу растепления скважин при их эксплуатации. Теоретических исследований процесса растепления ММП в процессе бурения скважины в настоящий момент недостаточно. Кроме того, нужно заметить, что в перечисленных работах используются математические модели, основанные, по сути, на решении уравнения теплопроводности, в которых в качестве граничных условий на стенках скважины задается температура флюида (в редком случае с коэффициентом теплоотдачи, который для буровых растворов неизвестен). Эти подходы не могут учесть свойства и режимы течения циркулирующего в скважине раствора. В отличие от ранее проведенных в этой области исследований в данной работе рассмотрен сопряженный теплообмен с учетом процесса растепления и циркуляции бурового раствора в скважине. Данный подход позволяет учесть влияние реальных физических свойств буровых жидкостей (вязкость, реология, теплофизические характеристики) и режимов их течения на величину коэффициента теплопередачи от бурового раствора к ММП и скорость распространения границы зоны растепления вокруг скважины.

В общем случае течение вязкой жидкости описывается системой уравнений Навье–Стокса, состоящей из уравнения сохранения массы:

д! + v( р v ) = 0                                                   (3)

и уравнения движения или закона сохранения импульса:

+ V ( р v . v ) = -V p + V ( t ) + F ,                                   (4)

где v – вектор скорости жидкости, τ – тензор вязких напряжений, F – вектор массовых сил, p – статическое давление, ρ – плотность жидкости. Поскольку в большинстве случаев буровой раствор представляет собой неньютоновскую жидкость, для моделирования неньютоновских течений мы использовали хорошо известный подход [17-18], в котором среда рассматривается как нелинейная вязкая жидкость с введением эффективной вязкости жидкости μ ( γ ), которая зависит от скорости сдвига. При этом тензор вязких напряжений τ определяется следующим образом:

т = A D ,                                                                 (5)

где μ – эффективная вязкость, D – тензор скоростей деформации.

Компоненты тензора скоростей деформации D имеют вид:

D A A axj ax

Cкорость сдвига ͘ γ является вторым инвариантом тензора скорости деформации:

Y = _А - D ■ D .

Исследуемая среда может являться как вязкой ньютоновской жидкостью, так и неньютоновской вязкопластической жидкостью, поведение которой описывается одной из трех наиболее распространенных реологических моделей: степенная жидкость, бингамовская жидкость (жидкость Бингама) и жидкость Гершеля-Балкли.

В зависимости от реологии бурового раствора, эффективная вязкость имеет вид:

p (y') = K - для ньютоновских жидкостей, здесь K - молекулярная вязкость раствора;

n — 1

А ( / ) = k v Y — Для модели степенной среды (Power-law);

A ( Y & ) = ( k j^- + т 0 ) /;& - для модели бингамовской жидкости;

Ц ( У" ) = ( kJ n + т о ) ,У – для модели жидкости Гершеля-Балкли, где k_v – показатель консистентности; n – показатель степени жидкости, τ ₀ – предельное напряжение сдвига.

При растеплении (промерзании) вечномерзлых грунтов происходит процесс плавления (кристаллизации). В данной работе для моделирования этих процессов используется формулировка энтальпия-пористость. В этом методе граница расплава не отслеживается в явном виде. Вместо этого вводится величина, называемая объемной долей жидкой фракции, которая указывает на долю объема ячеек, находящихся в жидком состоянии. Жидкая фракция вычисляется на каждой итерации на основе баланса энтальпии. В двухфазной зоне жидкая фракция имеет значение от 0 до 1. Она моделируется как псевдопористая среда, в которой пористость уменьшается от 1 до 0, что свидетельствует о затвердевании материала. Когда материал полностью – 116 – затвердевает в ячейке, пористость становится равной нулю и, следовательно, скорость также падает до нуля. Двухфазная зона жидкость-твердое тело рассматривается как пористая зона с пористостью, равной объемной доле жидкой фракции. Соответствующие источники стока (притока) энергии и импульса добавляются к сохранению энергии и сохранению импульса.

Для задач затвердевания/плавления уравнение энергии записывается в виде

д

6 t (pH )+V(P vH )-V( k V T) + S,(8)

где H – энтальпия; k – коэффициент теплопроводности; T – температура; S – сток импульса.

Энтальпия в свою очередь определяется как:

H- hH,(9)

h - href +jT Cp dT,(10)

re где ΔH – скрытая теплота фазового перехода; href – стандартная энтальпия образования вещества; Tref – стандартная температура; Cp – удельная теплоемкость при постоянном давлении.

Объемную долю жидкой фазы β можно определить как:

β = 0, если T <  T solidus ;

β = 1, если T <  T _liquidus;

„     T - T lid в = T-----^T^, если TSolidus < T < Tliquidus.

liquidus solidus

Скрытое теплосодержание теперь можно записать в терминах теплоты фазового перехода L :

A H = P-L .                                                             (11)

Подход энтальпия-пористость моделирует двухфазную область (частично затвердевшая область) как пористую среду. Пористость в каждой ячейке устанавливается равной доли жидкой фазы в этой ячейке. В полностью затвердевающих регионах пористость равна нулю. Сток импульса в связи с уменьшением пористости в двухфазной зоне имеет следующий вид:

_S -41 - в )1 A_ д ,) ,                                           (12)

3         mush

(e + 6 )

где β – объем жидкой фазы, ε – численный параметр (0.001), чтобы предотвратить деление на ноль, A mush – постоянная двухфазного региона.

Отметим основные моменты численной методики. Разностный аналог конвективнодиффузионных уравнений находится с помощью метода конечного объема для неструктурированных сеток. В этом случае полученная схема автоматически оказывается консервативной. Суть метода заключается в разбиении расчетной области на контрольные объемы и интегрировании исходных уравнений сохранения по каждому контрольному объему для получения конечно-разностных соотношений. Аппроксимация конвективных членов уравнений переноса осуществляется соответственно с помощью противопоточной схемы второго порядка QUICK.

Диффузионные потоки и источниковые члены аппроксимируются конечно-объемными аналогами центрально-разностных соотношений со вторым порядком точности. Связь между полями скорости и давления, обеспечивающая выполнение уравнения неразрывности, реализуется при помощи SIMPLEC – процедуры на совмещенных сетках. Для устранения осцилляций поля давления используется подход Рхи-Чоу, заключающийся во введение монотонизатора в уравнения для поправки давления. Полученные в результате дискретизации исходной системы дифференциальных уравнений разностные уравнения решаются итерационным способом с применением алгебраического многосеточного решателя.

Результаты тестирования описанной выше численной методики представлены в работах [19, 20]. Было получено хорошее согласие расчетов с экспериментом по форме профиля скорости бурового раствора в скважине, а также по динамике фронта процесса растепления.

Результаты исследования и их обсуждение

На основе разработанной методики проведены расчеты процесса растепления породы в процессе бурения скважины с помощью бурового раствора на основе смеси вода-этиленгликоль. При этом использовались теплофизические параметры мерзлой породы (плотность ρ , льди-стость i , коэффициент теплопроводности k и удельная теплоемкость C_p ), которые приведены в табл. 2. Температура мерзлых пород была задана равной минус 4 ºС.

При моделировании задавались геометрические параметры скважины, близкие к типичным конструкциям, применяемым при бурении. Диаметр скважины был равен 296 мм, диаметр бурильной трубы равен d = 125 мм. Глубина скважины задана равной L = 400 м, что соответствует средней глубине залегания ММП.

Расчет проводился в осесимметричной постановке. Радиус расчетной области 100 м, глубина расчетной области 600 м. Для расчета использовалась сетка, состоящая из 600000 ячеек. Сетка была сгущена к стенкам бурильной трубы и скважины. Методические расчеты показали, что такие размеры расчетной области и детализация сетки не влияют на результаты моделирования.

На входе в скважину в качестве граничного условия задавалось постоянное значение расхода бурового раствора, равное 40 л/с. Температура раствора задавалась равной 15 ºС. Пройдя по бурильной трубе до конца скважины, буровой раствор разворачивался и поднимался наверх по кольцевому зазору. На выходе из скважины задавались условия Неймана.

Максимальная длительность процесса бурения в расчете была принята равной 5 сут. При этом использовалось приближение, что буровой раствор подавался в скважину постоянно и бурение не останавливалось. Нагрев бурового раствора из-за трения о стенки скважины и долота не учитывался.

Таблица 2. Свойства породы

Table 2. Rock properties

ρ , kg/m 3	i, %	k , W/(m·K)	C p , J/(kg·K)
2110	50	1.67	2720

Свойства бурового раствора были заданы исходя из экспериментальных данных, приведенных в табл. 1. При моделировании реологии использовалась степенная модель.

На рис. 2 показаны типичные профили скорости в бурильной трубе и кольцевом зазоре, а также распределение объемной доли жидкой фазы и температуры бурового раствора и прилегающих к скважине горных пород. Видно, что температура бурового раствора в бурильной трубе и кольцевом пространстве практически однородна. Максимальная разность температуры бурового раствора в центре трубы и у стенки скважины не превышает 2 ºС.

Распределение температуры по радиусу r для разной длительности процесса бурения изображено на рис. 3. Как видно, на границе стенки скважины и породы температура испытывает резкое изменение. Анализ результатов при заданных параметрах показывает, что за неделю бурения расходом бурового раствора 40 л/с радиус зоны растепления ММП составляет примерно r = 0.35 м.

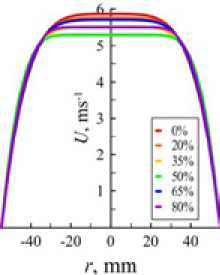
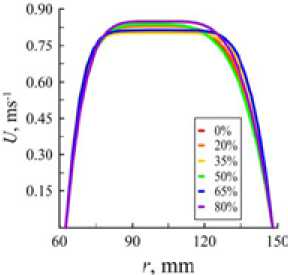
Далее было исследовано влияние содержания этиленгликоля в буровом растворе. На рис. 4 приведены профили скорости в трубе и кольцевом зазоре при разных концентрациях этиленгликоля. Проанализировано влияние добавки ЭГ на форму профиля скорости. Установлено, что добавление этиленгликоля при заданном расходе бурового раствора в целом приводит к уширению (выполаживанию) формы профиля скорости. Это уширение связано с уменьшением показателя степенной модели, которое происходит при увеличении концентрации этиленгликоля. Этот эффект наиболее заметен при концентрациях этиленгликоля 50-65 мас. %. Уширение профиля скорости благоприятно сказывается на эффективности выноса шлама при

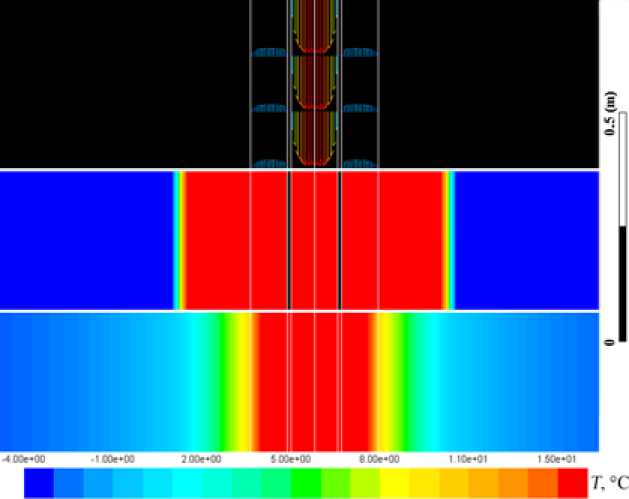
Рис. 2. Профиль скорости (a), распределение объемной доли жидкой фазы (б) и распределение температуры (в) в скважине и околоскважинном пространстве на глубине 200 м через 5 сут с момента начала бурения для базового раствора

Fig. 2. Velocity profile (a), the volume fraction distribution of the fluid phase (б), temperature distribution (в) in the well and near-well space for the base solution at a depth of 200 m in 5 days from the start of drilling

– 119 –

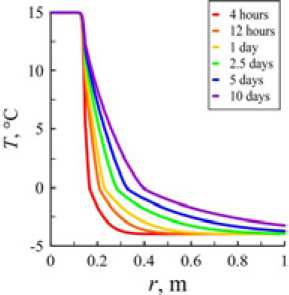
Рис. 3. Распределение температуры по радиусу на глубине 200 м от времени c момента начала бурения базовом раствором

Fig. 3. Temperature distribution over the radius at a depth of 200 m from the start time of drilling using by base solution

а )

Рис. 4. Профили скорости в бурильной трубе (а)

б )

и в кольцевом зазоре (б)

Fig. 4. Velocity profiles in the pipe drill (a) and in the annulus (б)

бурении: чем более однородный профиль скорости, тем эффективнее очистка ствола скважины от твердых частиц. Однако при этом необходимо следить за потерями давления при прокачивании бурового раствора. Повышение вязкости бурового раствора приводит к росту потерь давления. Зависимость перепада давления от содержания этиленгликоля приведена на рис. 5. Как видно, вплоть до концентрации 65 мас. % добавка этиленгликоля слабо влияет на величину перепада давления. При концентрации этиленгликоля 80 мас. % перепад давления повышается примерно на 30 % по сравнению с базовым раствором.

Далее, было проанализировано влияние добавки этиленгликоля на скорость процесса растепления. С точки зрения снижения скорости процесса растепления в процессе бурения важную роль играет теплопроводность и теплоемкость бурового раствора. Согласно данным, приведенным в табл. 1, с увеличением массового содержания этиленгликоля коэффициент теплопроводности и теплоемкость раствора существенно снижаются. Снижение коэффициента теплопроводности бурового раствора при бурении в условиях ММП является благоприятным – 120 –

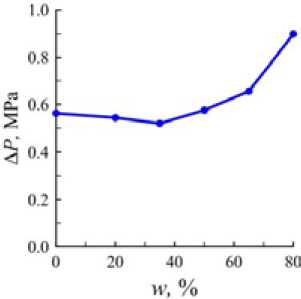
Рис. 5. Потери давления в скважине в зависимости от массовой концентрации этиленгликоля

Fig. 5. Well pressure drop depending on the mass concentration of ethylene glycol

а )

б )

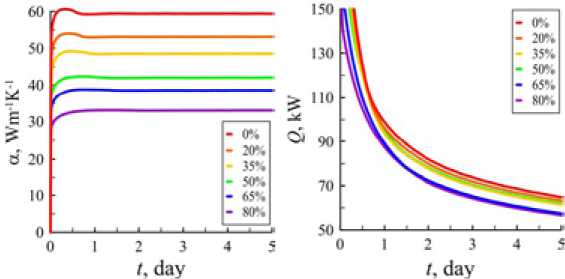
Рис. 6. Зависимость коэффициента теплоотдачи от стенок скважины (а) и тепловой поток, поступающий в скважину (б) от времени с начала бурения

Fig. 6. The dependence of the heat transfer coefficient of the well walls (a) and the heat flow entering the well (б) on the start time of drilling фактором для уменьшения скорости растепления, поскольку в этом случае уменьшается значение коэффициента теплоотдачи от раствора к стенкам скважины. Зависимость среднего по площади значения коэффициента теплоотдачи ᾱ от бурового раствора к стенке скважины от содержания этиленгликоля приведена на рис. 6а. Как видно, при увеличении содержания этиленгликоля в буровом растворе коэффициент теплоотдачи монотонно снижается. Это снижение довольно существенное. Так, при концентрации этиленгликоля 80 мас. % коэффициент теплоотдачи практически в два раза меньше по сравнению с базовым раствором. Также можно заметить, что коэффициент теплоотдачи, за исключением первых полчаса, практически не меняется. Коэффициент теплоотдачи при течении бурового раствора в скважине без учета его реологии можно оценить по известной формуле Nu = 1.55 ∙ (Re ∙ Pr ∙ d / L)0.33, где Nu, Re, Pr – числа Нуссельта, Рейнольдса и Прандтля. Нетрудно показать, что в этом случае коэффициент теплоотдачи при фиксированном значении расхода бурового раствора будет пропорционален комплексу α~ C p0.33 ⋅λ0.67. Согласно этим оценкам и данным табл. 1, раствор с 80 мас. % эти- ленгликоля за счет снижения теплопроводности и теплоемкости бурового раствора позволяет снизить коэффициент теплоотдачи от раствора к стенке скважины примерно в 1.8 раза. Это хорошо согласуется с полученными нами расчетными данными.

Снижение коэффициента теплоотдачи приводит к тому, что значение температуры на стенках скважины понижается, что приводит к снижению скорости процесса растепления. Распределение температуры по радиусу на глубине 200 м при различном содержании этиленгликоля в буровом растворе показано на рис. 7. Cнижение температуры на стенках скважины за счет уменьшения коэффициента теплоотдачи составляет около 3 °C по отношению к базовому буровому раствору.

Снижение теплоемкости бурового раствора, которое происходит при добавлении этиленгликоля, также является благоприятным фактором, поскольку в этом случае при прочих равных условиях снижается количество поступающего в скважину вместе с буровым раствором количество тепла. Это факт проиллюстрирован на рис. 6 б , на котором приведена зависимость от времени теплового потока при различном содержании этиленгликоля в буровом растворе. С увеличением содержания этиленгликоля количество тепла, поступающего в скважину, снижается. Особенно сильно этот эффект проявляется в первые сутки после начала циркуляции. По мере прогрева около скважинного пространства тепловой поток монотонно снижается. При этом снижается и эффект от добавки этиленгликоля в буровой раствор.

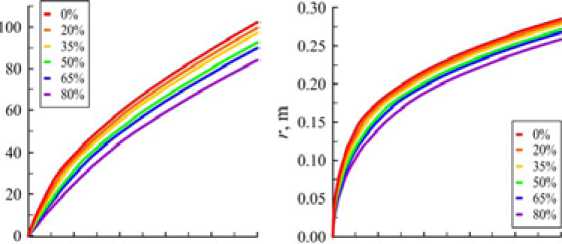
Снижение коэффициента теплоотдачи и количества тепла, поступающего в скважину, при добавлении в буровой раствор этиленгликоля совокупно приводит к значительному замедлению скорости процесса растепления ММП. На рис. 8 показана зависимость от времени с начала циркуляции объема растепленной вокруг скважины породы и среднего по глубине радиуса фронта растепления (от стенки скважины). Анализ показывает, что при увеличении содержания этиленгликоля происходит монотонное снижение этих параметров. При этом наиболее сильное снижение наблюдается в первые двое суток с начала циркуляции.

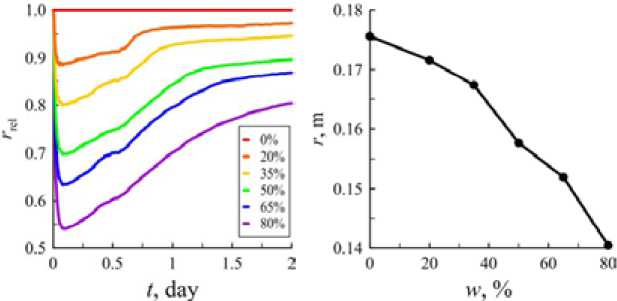
На рис. 9 а приведен отнесенный к радиусу растепления базового бурового раствора радиус растепеления при различном содержании добавки. Было установлено, что добавка 80 мас. % этиленгликоля приводит к снижению объема растепленной породы примерно в 3 раза, а радиуса растепления – в 1.7 раз. Это при условии, что бурение участка с ММП проводилось в тече-

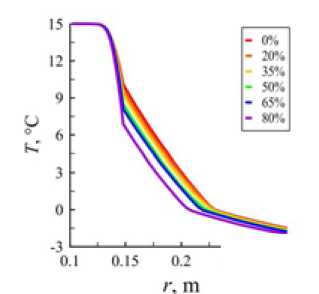
Рис. 7. Распределение температуры по радиусу на глубине 200 м через сутки после начала циркуляции

Fig. 7. The temperature distribution along the radius at a depth of 200 m after a day from the start of circulation

– 122 –

О I 2     3     4     5 V J 2     3     4     5

Л day                           t, day

а )                                          б )

Рис. 8. Зависимость растепленной породы (а) и радиуса растепеления вокруг скважины (б) от времени с начала бурения

Fig. 8. Dependence of the volume of permafrost thaw (a) and the thawing radius around the well (б) on the time after the start of drilling

а )

б )

Рис. 9. Зависимость относительного радиуса растепления от времени (а) и зависимость радиуса растепления от концентрации этиленгликоля в растворе (б) через 1 день после начала бурения

Fig. 9. Dependence of the relative thawing radius on time (a) and on the concentration of ethylene glycol in solution (б) 1 day after the start of drilling ние суток. Если циркуляция бурового раствора осуществлялась дольше, то эффект от добавки этиленгликоля снижается, но все равно остается довольно существенным. В этом случае объем растепленной породы уменьшается в 1.6 раза, а средний радиус растепления – в 1.3 раза. Это показано на рис. 9б, где отражена зависимость радиуса растепления от концентрации этиленгликоля за 24 ч после начала циркуляции.

Заключение

Разработана математическая модель сопряженного теплообмена скважины с учетом фазовых переходов и циркуляции бурового раствора в процессе бурения. Математическая модель учитывает реальные свойства бурового раствора (вязкость, теплопроводность, реология), – 123 – фактические параметры процесса бурения (расход раствора и скорость вращения бурильной трубы) и легко адаптируется к геометрии скважины.

С помощью разработанной математической модели проведено исследование применения полимерных растворов на основе смеси этиленгликоль-вода для бурения ММП. В расчетах были использованы данные лабораторных исследований свойств буровых растворов с этиленгликолем. Массовая концентрация этиленгликоля варьировалась от 0 до 80 %. Были измерены реологические и теплофизические характеристики рассмотренных растворов. Показано, что введение этиленгликоля приводит к значительному снижению коэффициента теплопроводности и теплоемкости раствора, без существенного ухудшения реологических характеристик.

В результате численного моделирования установлено, что добавление этиленгликоля при заданном расходе бурового раствора вызывает уширение (выполаживание) формы профиля скорости, что благоприятно сказывается на эффективности выноса шлама при бурении. При этом было показано, что добавка этиленгликоля слабо влияет на величину перепада давления в скважине. При концентрации этиленгликоля 80 мас. % перепад давления повышается примерно на 30 % по сравнению с базовым раствором.

Было установлено, что при увеличении содержания этиленгликоля в буровом растворе коэффициент теплоотдачи от раствора к стенке скважины существенно снижается. При концентрации этиленгликоля 80 мас. % снижение составило практически два раза по сравнению с базовым раствором. При этом с увеличением содержания этиленгликоля происходит существенное снижение количества поступающего в скважину тепла.

Снижение коэффициента теплоотдачи и количества тепла, поступающего в скважину при добавлении в буровой раствор этиленгликоля, совокупно приводит к значительному замедлению скорости процесса растепления ММП. Анализ результатов моделирования показал, что при увеличении содержания этиленгликоля происходит монотонное снижение объема и среднего радиуса области растепленной вокруг скважины породы. При этом наиболее сильное снижение наблюдается в первые сутки с начала циркуляции. Было установлено, что добавка 80 мас. % этиленгликоля приводит к снижению объема растепленной породы примерно в 3 раза, а радиуса растепления – в 1.7 раз, при условии, что бурение участка с ММП проводилось в течение суток. Если циркуляция бурового раствора осуществлялась дольше, то эффект от добавки этиленгликоля снижается, но все равно остается довольно существенным.

Таким образом, с помощью численного моделирования была обоснована возможность существенно уменьшить тепловое воздействие на ММП при их бурении с помощью растворов с добавкой этиленгликоля. Установлены основные закономерности сопряженных теплогидравлических процессов при бурении ММП с учетом циркуляции раствора и растепления. Получены в работе данные будут полезны при разработке буровых растворов для бурения в условия ММП.

Благодарности / Acknowledgements

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фонда науки в рамках научного проекта № 18-48-242009 «Исследование сопряженных тепло-гидравлических – 124 – процессов при бурении скважин и разработка рецептур буровых растворов для снижения скорости процесса растепления многолетнемерзлых пород».

The study was supported by the Russian Foundation for Basic Research, the Government of the Krasnoyarsk Territory, and the Krasnoyarsk Territory Science Foundation in terms of research project No. 18-48-242009 “The study of coupled thermohydraulic processes during well drilling and development of drilling fluid formulations for reducing the rate of permafrost thaw”.