Расчетное исследование радиальных сил, действующих на ротор радиально-осевой гидротурбины

основного потока. Для учета вышеупомянутых факторов необходимо проведение трудоемких численных расчетов в т.ч. в области всей проточной части гидроагрегата.

Предмет исследований. В общем виде полная гидравлическая нагрузка F, действующая на РК, складывается из 3 составляющих (рис. 1):

F = F 1 + F 2 + F 3 , (1)

где: F 1 – нагрузка от основного потока на поверхность РК; F 2 – нагрузка от течения через верхнее ЛУ; F 3 – нагрузка от течения через нижнее ЛУ.

В полной гидравлической нагрузке F выделяются осевые F z и радиальные F R (F x ,F y ) усилия. Радиальная сила F R (F x , F y ) тоже складывается из трех составляющих:

F R = F R, 1 + F R, 2 + F R, 3 , (2)

Возникновение радиальной силы FR,1 со стороны основного потока на проточную часть РК вызвано окружной неравномерностью потока в спиральной камере, а также окружной неравномерностью и нестационарностью потока за РК в конусе отсасывающей трубы (ОТ). Поэтому для определения радиальной нагрузки FR,1 моделирование течения необходимо проводить в полной постановке в области, включающей спиральную камеру, все межлопаточные и межлопастные каналы, а также ОТ. Возникновение сил FR,2 и FR,3 вызвано главным образом окружной неравномерностью потока в ЛУ вследствие смещения центра вращения РК относительно геометрического центра камеры РК. Поэтому для определения сил FR,2 и FR,3 моделирование течения в ЛУ необходимо осуществлять не в сегменте, а во всей области зазоров по ЛУ.

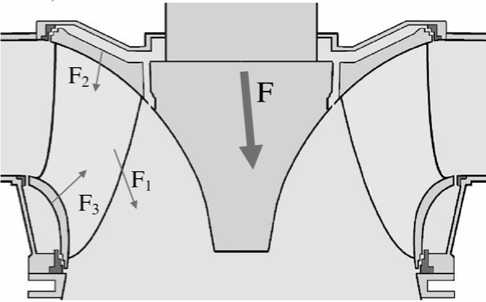
Рис. 1. Силы, действующие на РК

Объект исследований. В качестве объекта для исследования нагрузок на РК принята гидротурбина (ГТ), параметры которой представлены в таблице 1. На рис. 2 показана расчетная область в системе координат РК.

Таблица 1. Параметры исследуемой ГТ

номинальная частота вращения	n	200 мин-1
диаметр рабочего колеса	D 1	3,15 м
высота направляющего аппарата	B 0	0,997 м

Течение в кольцевом зазоре переменной ширины приводит к появлению радиальных сил, действующих со стороны протекающей в зазоре жидкости. Используются две методики расчета радиальной составляющей нагрузки F 2 в модели с эксцентриситетом. Первая методика основана на расчете трёхмерного течения в несимметричной щели, в основе второй лежит инженерноэмпирический подход А.А. Ломакина [5].

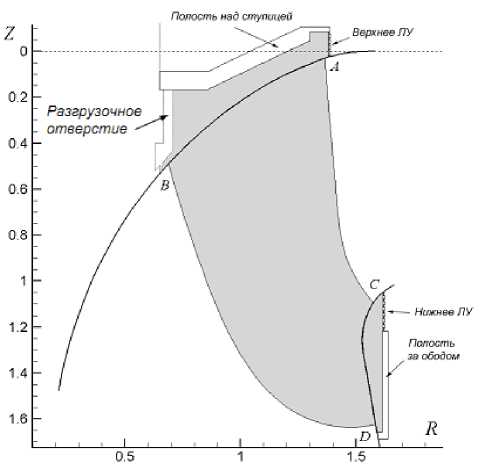
Рис. 2. Области протечек за ступицей и ободом РК

При расчете радиальной нагрузки на рабочее колесо интерес представляют следующие режимы (таблица 2): режим номинальной мощности и режим неполной нагрузки.

Течение в основной части ГТ: нагрузка F 1 и данные для течений в лабиринтах. Течение в основной части ГТ рассчитывается в полной нестационарной постановке, в натурных параметрах, в невязком приближении, в области, указанной на рис. 3.

Течение в уплотнениях. Для определения радиальной составляющей нагрузки F 2 используется модель течения в ЛУ со смещенной осью РК. Полагаем, что имеются смещение оси РК на эксцентриситет e и её прецессия вокруг центра статорной части с угловой скоростью Ω (рис. 4)

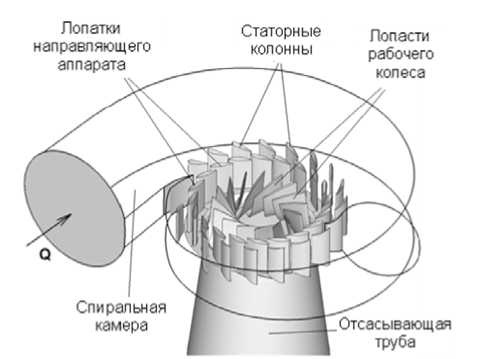
Рис. 3. Расчетная область для определения F 1 и данных для течений в лабиринтах

Таблица 2. Режимы при расчете номинальной нагрузки на РК

Параметры	Режим 1	Режим 2
напор H, м	78,3	73,5
открытие НА a 0 , мм	222	123,3
открытие НА модели a 0,мод , мм	32,4	18
расход Q, м3/c	87,98	50,61
высота отсасывания H s , м	–0,2	–4,2

Экспериментальные данные. В ходе испытаний были замерены радиальные усилия |F R | в диапазоне открытий направляющего аппарата от 14 до 36 мм для приведенных частот n 1 ' = 71,2, 73,5, 76,1 об/мин. В таблице 3 представлены статическая |F R | st и динамическая |F R | dyn составляющие радиального усилия, как измеренные на модели, так и пересчитанные на натурную ГТ.

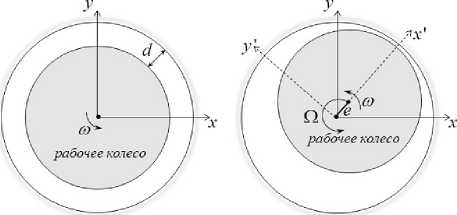
Рис. 4. Кольцевая щель лабиринтного уплотнения: a) ось вращения РК совпадает с центром полости; б) ось вращения РК смещена относительно центра полости

Таблица 3. Радиальное усилие |F R | на направляющий подшипник ГТ

Режимы	Модельная ГТ		Натурная ГТ
	|F R | st , кгс	|F R | dyn , кгс	|F R | st , тс	|F R | dyn , тс
режим 1	39,53	31,92	6,048	4,883
режим 2	36,36	21,32	5,221	3,061

На рис. 5 показаны спектрограммы пульсаций радиального усилия. Для режима 2 (a 0,mod =18 мм) прослеживается частота f=0,22 f n , вызванная вращением вихревого жгута. Однако наибольшую амплитуду пульсаций радиальной и осевой силы в обоих режимах дает оборотная частота f n . Это указывает либо на прецессию оси вращения РК с частотой, равной частоте его вращения (например, изгиб вала), либо на отсутствие симметрии модельного РК.

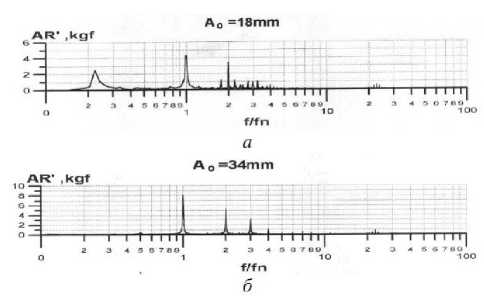
Рис. 5. Спектрограммы пульсаций радиального |F R | усилия (а – режим 2, б – режим 1), полученные при испытаниях модели

Результаты расчета в режиме номинальной мощности (режим 1). Расчеты проведены в натурных параметрах с учетом силы тяжести (g=9,81 м/с ² ) с шагом по физическому времени ∆ t =0,003126 с, который соответствует повороту РК на угол θ=3,75°. Расчеты проведены в программном комплексе CADRUN [1]. Построение сеточных областей выполнялось в системе АСТРА. CADRUN – программный комплекс для расчета гидродинамики гидравлических турбин и насосов, разработанный Институтом вычислительных технологий СО РАН; АСТРА – программный комплекс для построения геометрии, расчетных сеток и управляющих программ станков ЧПУ сложных объектов (в т.ч. лопастей ГТ и насосов), разработанный ИМ СО РАН.

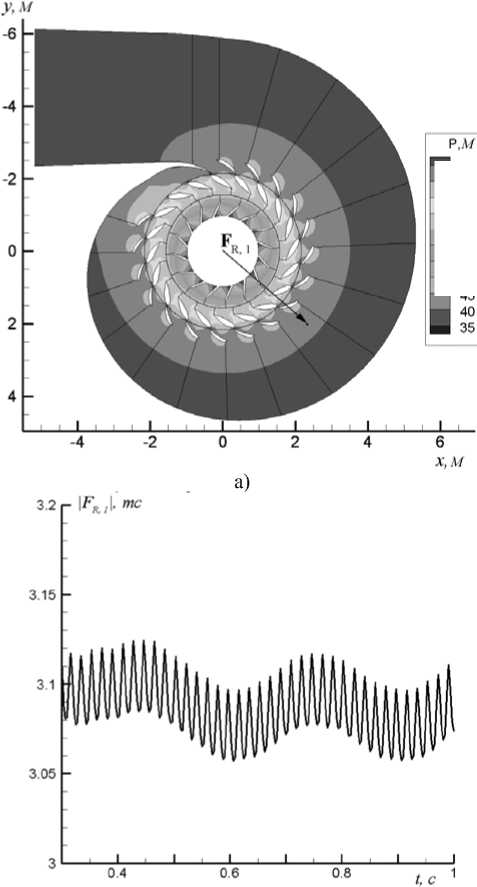
На рис. 6 показаны изолинии давления в конусе ОТ. Явно видна осесимметричная область пониженного давления в центре конуса ОТ. Период пульсаций F R,1 , полученных в расчете (рис. 7б) равен T=0,01875 с, что соответствует их частоте f b =1/T= 53,28 Гц. Частота вращения ротора равна f n =200 об/мин*1/60=3,33 Гц. Отношение частот f b /f n =1/16 равно количеству лопастей РК, т.е. наблюдаемые пульсации обусловлены лопастной системой РК. Среднее значение модуля радиальной силы: \FR ,1 = J F X,1 + F? 1 = 3.007 тс . Амплитуда колебаний в этом режиме очень мала (рис. 8). На рис. 7а показано направление действия силы F R,1 относительно решетки статора ГТ.

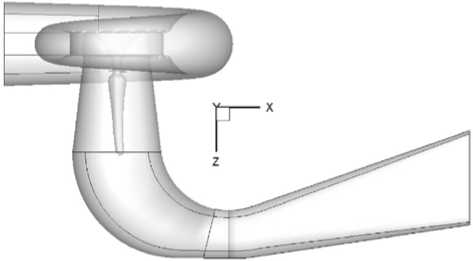
Рис. 6. Вихревой жгут в ОТ (режим 1)

На рис. 9. показано, что прецессия вала с частотой Ω= ω R заметно увеличивает радиальную силу при больших эксцентриситетах, что ограничивает использование эмпирической методики при Е > 0,5.

Результаты расчета в режиме неполной загрузки (режим 2). Для режима 2 характерно наличие прецессирующего вихревого жгута в конусе ОТ (рис. 10). Движение вихревого жгута вызывает пульсации давления не только на стенке конуса ОТ, но и вверх по потоку.

■ 85

■ 80

— 70

■ 60

■ 55

- 50

■ 45

б)

Рис. 7. а) направление действия радиальной силы F R,1 и мгновенное распределение давления в сечении Z = b 0 /2. Масштаб силы 1 м = 1 тс. б) пульсации радиальной составляющей F R,1

Частота прецессии вихря f v =0,741 Гц = 0,222 f n явно выделяется в пульсации радиальной нагрузки, действующей на РК (рис. 11б, 12). Статическая радиальная сила F R,ст определяется как средняя по пульсациям, динамическая – как половина размаха пульсаций:

F

R ,max

R , дин

—

F

R ,min

Величина пульсаций F R составляет порядка 100% от средней величины (рис. 11).

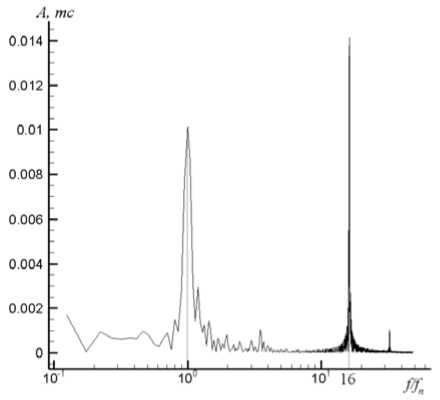
Рис. 8. Спектрограмма пульсаций радиального усилия |F R,1 | , полученного в расчете на CADRUN для режима 1

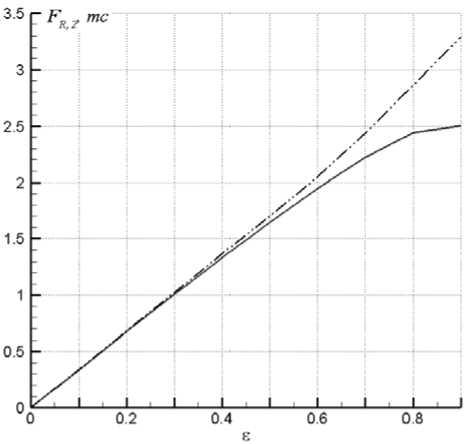
Рис. 9. Влияние частоты прецессии Ω на зависимость модуля радиальной силы F 2,R от относительного эксцентриситета ε . (—) CADRUN, Ω = 0, (-⋅⋅-) CADRUN, Ω = ω R

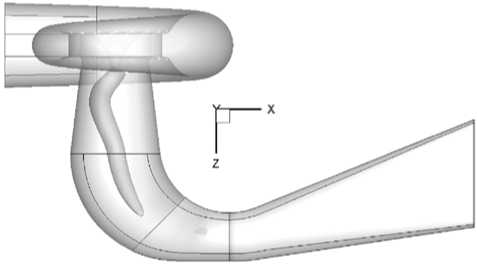
Рис. 10. Вихревой жгут в ОТ (режим2)

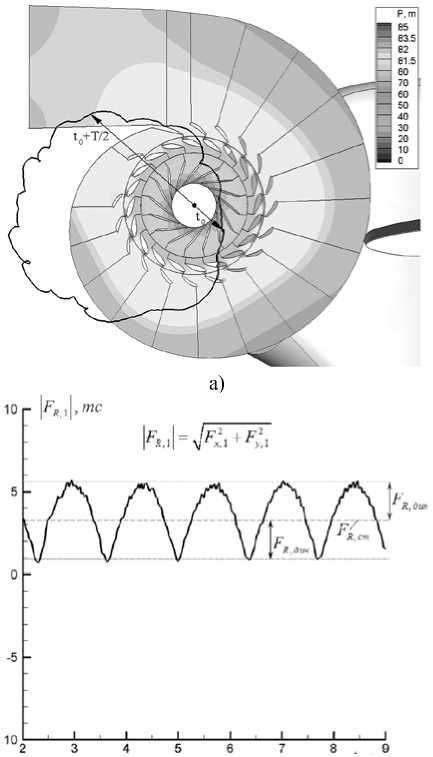
б)

Рис. 11. а) годограф радиальной силы F R,1 на периоде T прецессии вихря и мгновенное (t=t 0 ) распределение давления в сечении Z = b 0 /2. б) пульсации радиальной составляющей F R,1 нагрузки

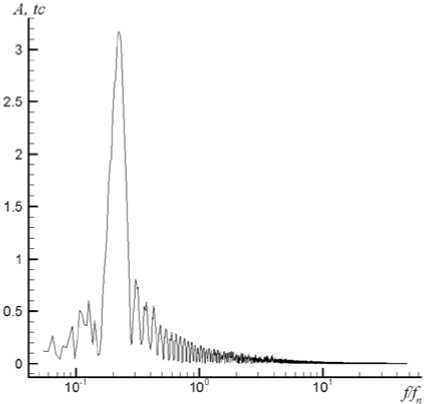
Рис. 12. Спектрограмма пульсаций радиального усилия |F R,1 | , полученного в расчете на

CADRUN2 для режима 2

Для нахождения F 2,R (рис. 13) проведены расчеты трехмерного течения в области верхнего ЛУ с эксцентриситетом. Давления на входе в верхнее ЛУ (p A =45,5 м) и на выходе из него (p out, l = 18,3 м) взяты из расчета стационарного течения в области верхнего лабиринтного уплотнения.

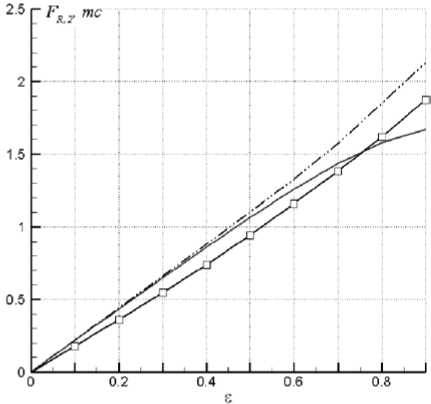
Рис. 13. Зависимости радиальной силы F R,2 от относительного эксцентриситета ε, (- □ -) – улучшенная инженерно-эмпирическая методика, (—) – CADRUN, Ω=0, (-⋅⋅-) – CADRUN, Ω=ω R

Обобщение результатов. Результаты для радиальной силы представлены для случая несо-осности статора и ротора с эксцентриситетом e = 0.8d 1 , где d 1 – ширина узкой части щели верхнего ЛУ. В таблице 4 показаны суммарные радиальные нагрузки на обоих режимах.

Выводы: разработана методика определения нестационарных радиальных нагрузок на рабочее колесо радиально-осевой гидротурбины, основанная на трехмерных расчетах течения несжимаемой жидкости в проточной части и областях протечек. Методика позволяет рассчитать радиальные нагрузки, вызванные следующими факторами: неравномерностью потока в спиральной камере и статоре; ротор-статор взаимодействием; неравномерностью потока за РК вследствие нестационарности потока в конусе ОТ (вихревой жгут и т.д.); несо-осностью статора и ротора, изгибом вала ротора.

Таблица 4. Радиальная сила F R , тс

Режим	F R,1	F R,2	F R,3	F R
1	3,077±0,03(16f n )	±2,4(f n )	±3,9(f n )	3,1±6,3 (f n )
2	3,3±2,3(0,222f n )	±1,55(f n )	±3,3(f n )	3,3±2,3(0,222f n )±4,9(f n )