Расчетное исследование влияния режимных параметров на теплообмен в алюминиевом электролизере

Описание математической модели. Эффективность работы электролизера во многом определяется его тепловым состоянием. Однако детальные эксперименталь ные исследования влияния режимных параметров на теплообмен в электролизере затруднены. Поэтому наибо лее рационально использовать расчетные методы анали за процесса электролиза.

Анализ источников показывает, что для проведения расчетов теплового состояния алюминиевых электролизеров можно ограничиться стационарным уравнени ем теплопроводности с внутренними источниками теплоты. При этом влияние гидродинамики электролита и расплавленного металла на теплоперенос можно учесть за счет введения эффективного коэффициента теплопроводности.

В данной статье предложена математическая модель теплообмена в электролизере (рис. 1), где температурное поле футеровки и расплава определяется согласно стаци онарному двумерному уравнению теплопроводности с учетом ортотропии среды. Для расчета внутреннего ис точника теплоты использован подход, в котором исклю чается решение задачи электрического потенциала во всем объеме электролизера. Правомерность такого допущения связана с тем, что наибольшая мощность внутренних источников теплоты qv (95 %) выделяется в межполюсном пространстве (МПР) [1].

При разработке математической модели принято, что распределение температур в рабочем объеме электро лизера подчиняется уравнению теплопроводности, представленному в следующем виде [2; 3]:

д дx 2

AlA tvE

_ I x(xi,т)

д х,

1 V

Х(х2,T)|T + qv (Xi,х2 ) = 0, дх 2

где q v - объемная плотность внутренних источников теплоты, задаваемая в МПР, Вт/м³.

Запись уравнения (1) является обобщенной постановкой стационарной задачи Стефана, в которой путем введе- ния скачка теплопроводности учитывается заранее неизвестная граница раздела фаз «расплав - твердое тело» [1; 2]:

■ X т, т < т,

^Х р , ^т >  т ,

где T - температура фазового перехода, К; X _т , Х _р - коэффициенты теплопроводности твердой и жидкой фаз соответственно, Вт/(м • К).

На стыке слоев футеровки, состоящей из материалов различных физических свойств, использовалось гранич ное условие четвертого рода:

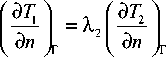
T 1 = T 2 ,

где T , T ₂ , Х 1 , Х ₂ - соответственно температуры и коэффициенты теплопроводности соприкасающихся сред. По условию (3) следует, что на границе раздела сред отсутствуют процессы, сопровождающиеся выделением или поглощением теплоты.

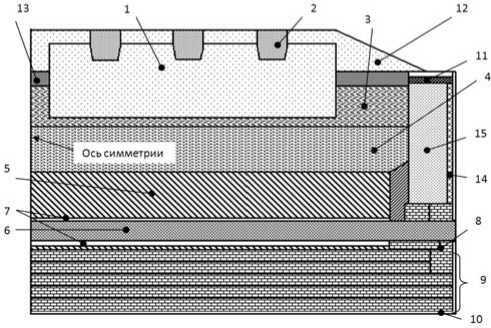
Рис. 1. Конструкция алюминиевого электролизера в поперечном сечении: 1 - анод; 2 - штыри; 3 - электролит; 4 - металл; 5 - подовый блок; 6 - блюмс; 7 - блюмсовая заделка; 8 - бровка; 9 - цоколь; 10 - стальной кожух; 11 - подфланцевая засыпка; 12 - глинозем; 13 - корка;

14 - уплотняющая шамотная засыпка; 15 - бортовой блок

На верхней, правой и нижней поверхностях расчетной области принималось граничное условие третьего рода (уравнение Ньютона-Рихмана) с учетом лучистой составляющей теплового потока:

—xfir 1 = аТ — Т_ )+еоТп4, (4) V д n 7с на оси симметрии модели - граничное условие второго рода (адиабатическая поверхность):

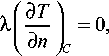
здесь а - коэффициент конвективной теплоотдачи;

Т_п , Т _{о с} - температура внешней поверхности и температура окружающей среды соответственно; е - степень черноты; о - постоянная Стефана-Больцмана; индекс С - обозначает, что градиенты температуры находятся на внешней поверхности твердого тела.

Численный метод решения. Дискретизация уравнения (1) проводилась с использованием центрально-разностной равномерной сетки с шагом h 1 по направлению х 1 и шагом h 2 по направлению x 2 . В результате была получена пятиточечная система нелинейных уравнений [4] (рис. 2).

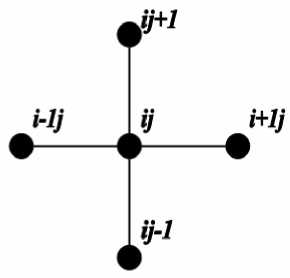
Рис. 2. Центрально-разностный пятиточечный шаблон (крест)

Уравнение (1) в результате дискредитации приняло вид сеточного уравнения:

• —л Т , -b Т , + d Т — aij^i - 1 j ^иij ^ij - 1 ⁺ j ij

• -а , Т , -b J , = f , ai + 1 j^i + 1 j ^vij + 1^X ij + 1 ^f jj ,

i- 1, 2, _,N i - 1, j -1, 2, ..., ^ 2 -1, (6) где N₁,N₂ - количество узлов в расчетной области по горизонтали и по вертикали.

Решение сеточной системы уравнений (6) проводилось итерационным методом сопряженных градиентов с выбором сеточного оператора согласно методу приближенной факторизации [2].

С целью приведения расчетной области задачи к прямоугольнику был использован метод фиктивных областей, который основан на дополнении исходной расчетной области до некоторой регулярной области. Решение исходной задачи было продолжено в фиктивную область, находящуюся над стальным фланцем катодного кожуха.

Апробация математической модели. Апробация разработанной математической модели проводилась путем сравнения полученных результатов расчета с данными промышленных опытов. Сравнение показывает качественно правильный характер изменения температурных кривых, полученных при расчете. Значения расчетных температур и тепловых потоков на кожухе (на уровне поверхности раздела «металл-электролит») были близки к измеренным. Максимальное расхождение температур расплава вблизи бортового блока не превышало 3,0 %. Некоторые результаты для сравнения приведены в таблице.

В качестве примера приведем расчетное двумерное температурное поле электролизера для принятых из практики его работы значений силы тока 130 кА и МНР 6 см (рис. 3). Температурное поле в поперечном сечении электролизера имеет значительную неравномерность. Наибольший градиент температур наблюдается в теплоизоляционных слоях футеровки, а также на границе раздела «расплав-гарнисаж» вблизи бортового блока.

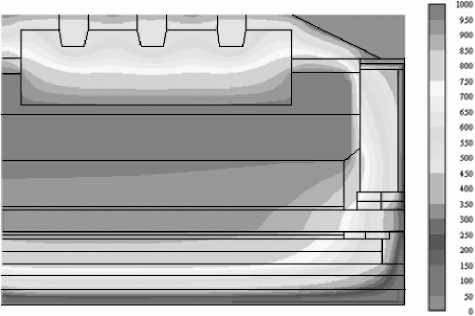
Рис. 3. Температурное поле электролизера в поперечном сечении

Отметим, что сила тока/оказывает влияние на интенсивность как восстановления алюминия на катоде, так и нагревания электролита [5]. Нрактика показывает, что на тепловое состояние электролизера существенное влияние оказывает также величина МНР. Увеличение величины МНР приводит к повышению температурного уровня в электролизной ванне, а уменьшение - к его снижению. Кроме того, при уменьшении МНР возникают нестабильности в работе электролизера из-за возможного соприкосновения жидкого алюминия с анодом. Ноэтому для поддержания в рамках технологического регламента необходимой температуры расплава t _p (в пределах 965.. .970 ° С) принятому значению 7 должна соответствовать определенная величина МНР.

Сравнение результатов расчета с данными, полученными в ходе проведения промышленных экспериментов

Параметры	Эксперимент	Двумерная модель
Температура электролита, ° C	954	955
Гарнисаж (толщина застывшего электролита между анодом и бортовым блоком), см	3,0	5,5
Настыль (толщина застывшего электролита на поверхности катодного блока), см	0	0
Температура катодного кожуха на днище, ° C	83	61
Температура катодного кожуха на верхнем поясе по продольной стороне, ° C	230	219
Температура катодного кожуха на среднем поясе по продольной стороне, ° C	185	177
Температура катодного кожуха на нижнем поясе по продольной стороне, ° C	73	66
Температура анодных штырей, ° C	380	450

Численные эксперименты. Оценка зависимости МПР от/ при условии поддержания величины t _p в указанных выше пределах проводилась с помощью численного эксперимента. Анализ результатов расчета показывает, что зависимость между МПР и / носит линейный характер (рис. 4). При условии t _p = const изменение величины / на 1 кА сопровождается изменением МПР примерно на 0,1 см (ДМПР ~ 0,1 см/кА). Практическое использование полученной зависимости может повысить надежность работы электролизера при варьировании его производительности в широких пределах.

кой кожуха. Было установлено, что относительное изменение толщины защитного слоя застывшего электролита от образовавшегося воздуха в пространстве между бортовым блоком и стенкой кожуха составляет примерно 0,1 мм на 1 % содержания воздуха (рис. 6). А в случае полного заполнения воздухом пространства между бортовым блоком и стенкой кожуха максимальная температура в рабочей области составляет примерно 1 005 °C (рис. 7). Такой тепловой режим работы электролизной ванны полностью исключает образование защитного слоя гарнисажа на боковых стенках.

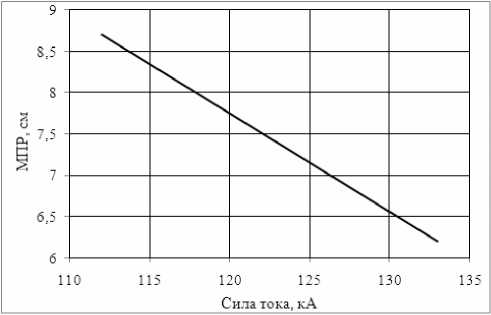
Рис. 4. Зависимость межполюсного расстояния МПР отсилытока / притемпературерасплава t _p = 965...970 ° C

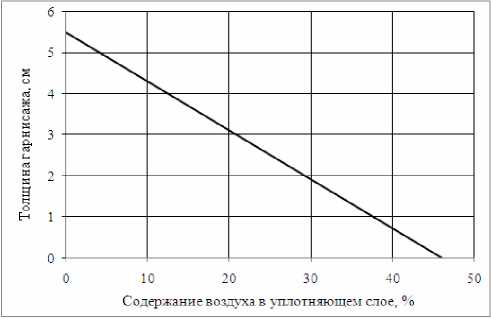
Рис. 6. Зависимость толщины гарнисажа от процентного содержания воздуха в уплотняющем слое

При футеровании электролизера, а также в процессе его работы между бортовым блоком и кожухом могут образовываться воздушные прослойки, которые значительно увеличивают термическое сопротивление. Возрастание термического сопротивления вызывает соответствующее увеличение температуры в рабочей области. В результате возникает опасность расплавления защитного гарнисажного слоя на внутренней поверхности бортового блока и его интенсивного изнашивания. Это обстоятельство может в дальнейшем привести к прорыву расплава через борта электролизера (рис. 5).

Расчетная оценка влияния образовавшихся воздушных прослоек на температурное поле электролизера проводилась при помощи соответствующего изменения значения коэффициента теплопроводности уплотняющего слоя между бортовым угольным блоком и стальной стен-

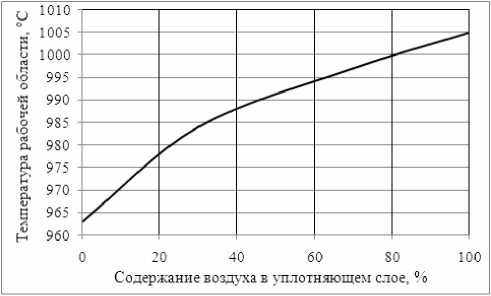
Рис. 7. Зависимость максимальной температуры рабочей зоны от процентного содержания воздуха в уплотняющем слое

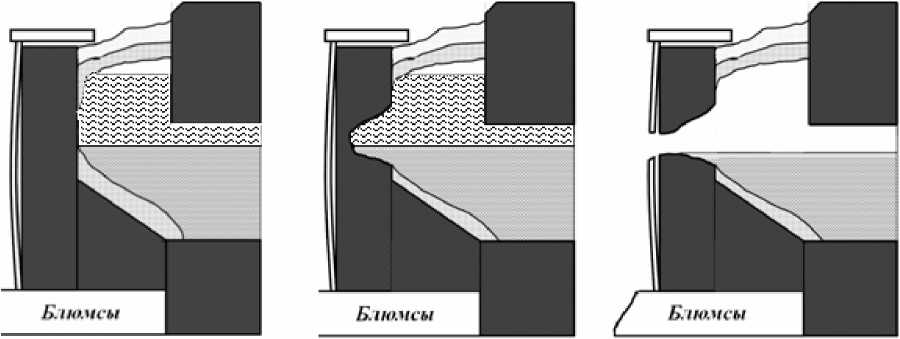
Рис. 5. Разрушение бортового блока от эрозионного воздействия расплава

Таким образом, разработана математическая модель теплообмена в алюминиевом электролизере. Показано, что модель обладает быстрой сходимостью решения и позволяет без сопряженного решения уравнений магнитной гидродинамики с достаточной для практики степенью точности проводить тепловые расчеты электролизера с учетом его конструктивных и технологических особенностей. Установлена зависимость величины межполюсного пространства от силы тока, а также толщины гарнисажа и температуры в рабочей области от наличия воздушных зазоров в пространстве между стальным кожухом и бортовым блоком.