Расчетное моделирование течения в полости дискового насоса

Дисковые насосы представляют собой простейшие турбомашины, в которых рабочему телу сообщается энергия за счет работы кориолисовых сил в форме сил терния. Основным элементом дискового насоса является расположенное в корпусе колесо, состоящее из нескольких дисков, скрепленных между собой. Дисковые насосы имеют ряд преимуществ по сравнению с лопастными машинами, а в некоторых областях они являются единственными работоспособными [1]. Учитывая, что дисковые насосы обладают исключительными антикавитационными свойствами, что позволяет более эффективно перекачивать двух- и трехфазные среды, имеют низкий уровень шума, они получили широкое применение в нефте- и горнодобывающей, химической, пищевой промышленностях, медицине. Кроме того, дисковые насосы эффективно работают в области малых коэффициентов быстроходности (при малых объемных расходах и высоких напорах), что в сочетании с антикавитационными качествами определяет их применение в энергосистемах малой мощности (< 100 кВт), использующих фазовый переход рабочего тела: паротурбинные генераторы на низкокипящем рабочем теле, системы терморегулирования различного назначения и т. п.

Для моделирования течения в рабочей полости дискового насоса целесообразно выделить структурно-функциональные участки гидравлического тракта, на которых реализованы различные типы течения.

Причем течение на каждом участке условно делится на течение в ядре и пространственном пограничном слое (ППС) [2]. Решение задачи о течении в ППС сводится к определению напряжений трения на непроницаемых границах. Результатом решения задачи о течении в ядре потока являются поля угловой скорости вращения ядра потока и статического давления. Согласно принципиальной схеме дискового насоса (рис. 1), нами были рассмотрены два следующих участка: с течением между вращающимся диском и неподвижной стенкой (рис. 1, полость В) и с течением межу двумя вращающимися дисками (рис. 1, полость А). Рассмотрим каждый из этих участков по отдельности.

Рассмотрим элементарный объем жидкости в зазоре между двумя вращающимися дисками (рис. 2). На рисунке τ0д1α, τ0дα2 – окружные напряжения трения на первом и втором диске соответственно; τ0д1Rα, τ0дR2α

–

радиальные напряжения трения от окружной составляющей скорости на первом и втором диске соответственно; τ ₀ ^д1 _Rр , τ ₀ ^д _R ² _р – радиальные напряжения трения от расходной составляющей скорости на первом и втором диске соответственно. Элементарный объем представляет собой кольцо на текущем радиусе высотой dR → 0 и толщиной z ₁ – нормальный зазор полости.

Рис. 1. Принципиальная схема дискового насоса:

1 – рабочее колесо; 2 – приводной вал; 3 – корпус; 4 – радиальное отводящее устройство; А – рабочая полость между двумя вращающимися дисками; В – полость между вращающимся диском и неподвижной стенкой

диск 1

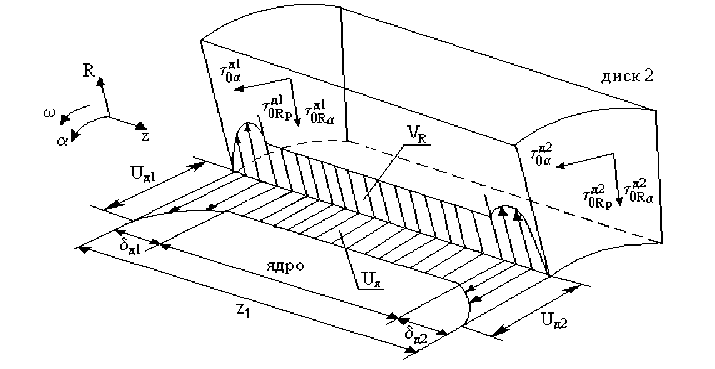
Рис. 2. Расчетная схема для полости между двумя вращающимися дисками

Бесконечно малый элементарный объем делится на три участка: течение в ППС около двух вращающихся дисков и течение ядра потока. Течение на первом диске происходит в толщине пограничного слоя 5 _д1, где окружная скорость жидкости изменяется от U _д1 – скорость вращения первого диска, до U _я – скорость вращения ядра потока. Течение на втором диске происходит в толщине пограничного слоя 5 _д2, где окружная скорость жидкости изменяется от U _я до U _д2 – скорость вращения второго диска.

Интегрированием системы уравнений импульсов турбулентного ППС в работе [3] получены составляющие напряжений трения на дисках в окружном и радиальном направлениях от окружной составляющей скорости:

– окружные напряжения трения на диске:

– радиальные напряжения трения от окружной составляющей скорости на диске:

т 0 R а =е д^д а , (3) где е д i , i = 1,2 - тангенс угла скоса донной линии тока на первом и втором дисках соответственно;

– радиальные напряжения трения от расходной составляющей скорости (определяются классическими выражениями [4]) на диске:

т

д i

0 Rр

0,01256 р V R

V r 5 а д

— -0,25

V

^т да = 0^,012⁵6 р ( _Ю д i -® я ) 2 х

₂ гк-®я) r 5:_Я1 Т²⁵         (1)

2 д          я      ^{а д} i

где ю д i , 5_{а д} i , i = 1,2 - угловые скорости вращения и толщины вытеснения пограничного слоя для первого и второго дисков соответственно; ю _я - угловая скорость вращения ядра потока.

Поскольку радиальная составляющая напряжения трения формируется как окружным, так и расходным (радиальным) течением, выражение для радиального напряжения на диске имеет вид:

^Т 0 R = ^т д Rp + ^т д Rа , ⁽²⁾

где т Д R , i = 1,2 - радиальная составляющая напряжения трения на первом и втором диске соответственно;

Полученные напряжения трения позволяют интегрировать уравнения движения вязкой несжимаемой жидкости в цилиндрических координатах [5] в граничных условиях полости между двумя вращающимися дисками:

д V_R  U, д V     д V_R  U 2     1 д p  1 9тп

V_R R + -я- R + V zR я- = p + R ;

дR   R да     дz   R    р дR  р дz ди и ди  т. дU vrux    1 дp 1 дта

V„    я + я + V.   я + ^{R я} = +   ;

д R   R да     д z    R     р R да р д z

Vr ^Vz.+ия ^V,+vz дЕ, = -1 дР +1 дт,;(5)

дR   R да     дz    р дzр д д VR 1 д ия  д VV

—R +--я + —z_ + _R_ = 0, дR R да   дzR

где U _я, V_R , V_z , т_а , т _R , т _z - проекции скорости и

напряжения трения на оси цилиндрической системы координат а , R , z соответственно.

Преобразуем систему (5) с учетом следующих допущений:

– течение в осевой щели осесимметрично, члены с равны нулю;

да

– в осевом направлении (в направлении z) течение д V „ дp         _ отсутствует, следовательно ---= 0 , — = 0 , V - 0;

д z        д z        '

Заменим постоянный параметр C_R на более упот-

третье уравнение системы (5) обнуляется;

– свойства жидкости постоянны;

– жидкость течет по гидравлически гладким поверхностям;

– течение происходит при турбулентном режиме.

Получаем следующие выражения:

ребительный параметр V , учитывая (7):

V

V R - Cr ; V_R  ------.

^{R 0 0 R}    R ⁰    2 n R ₀ z ,

Тогда

■

C r - -V- .

2 n z ,

V dV R _ /  _-_ 1 dp ₊ 1 дт R .

R dR R p dR p дz ’ dU VrU,  1 дта я Rя       а

V O +                      ;

^R dR R p д z

Выразим производную по ® _я из первого уравнения системы (9) с учетом (10). Согласно расчетной схеме при течении от центра к периферии получим:

^d ® я dR

2П( p V

д1

^т 0а

д2

^{+ т} 0а )

² ® я

R

dV V

—R + - R- - 0

dR R

Аналогично изложенному выше, выразим из второго уравнения системы (9) производную по p :

Третье уравнение системы (6) – уравнение неразрывности – интегрируется как уравнение с разделяющимися переменными:

Г dVRI"

J VRR "

В результате получаем:

VrR - const - VR R - Cr ,(7)

RR ₀ 0 R ,

dp _2d    p V ²

— - pшя R +---—-—— + dR         4n n2R3

1 д1 д 2

⁺ n ₀ ^(т 0 ^R ( “ )     ^{0 R} ( “ )

д1         д2

^T 0 R ( р )    ^т 0 R ( р ) ) .

Полученные выражения позволяют провести численное интегрирование и получить поле угловой ско-

где V_R – радиальная составляющая скорости в ядре потока; C_R – определяется граничными условиями на входе.

Сделанные допущения формулируют задачу в следующей постановке: поток разделяется на невязкое ядро, в котором члены не зависят от координаты z и тонкий пограничный   слой,   в котором дт         its т - J — dz - т|та - t5 - t0 - -т0. Проинтегрируем пер вые два уравнения системы (6) по z в пределах от 0 до z1 (причем в первом приближении не учитываем толщину вытеснения пограничных слоев). Подставив в полученную систему выражение (7), получаем:

рости в ядре потока и поле статического давления, которые в достаточной мере позволяют оценить характер движения рабочего тела в полости между дву-

мя вращающимися дисками.

Приращение по радиусу выбираем в зависимости от количества шагов расчетного алгоритма (требуемой точности):

R

N

( Cr dU,  C_RU )     т_Оа

, R я  I    R я __      0а.

'1---1-------- ----

1 ( R dR    R2 Jp

где R – радиус диска; N – число шагов алгоритма.

Тогда радиус на i -м шаге: R i - R i _, + A R , i - 1... N .

Далее для определения напряжений трения необходимо вычислить толщины потери импульса на дисках.

Толщина потери импульса на первом диске:

| ^C R , ^U я | ^z 1 ^dp , ^T 0 R z ,---- +-------1-- .

I R ³    R J p dR p

( а д; ) _/ = ( ^ : ;, ) ,

I ® д1

Перепишем систему (8) с учетом касательных напряжений трения, при этом учтем U - ю _я R , где ю _я - угловая скорость вращения ядра потока:

где

+

I ^Юд1 ( ® я ) i _J ^R i        +

_ ( ® я ) i _1|² R i + ( Cr/ R i ) 2 ⁺

( Cr/R , :)²

2 ^, I® д1 _ ( ® я ) i _J R i + ( Cr/R )²

_

f ^C R ^d ( ® я ^R ) , ^C R ® я ¹

( R dR R ^{J 1}

1 д1

I T0a

p

;

- 0,036 l -R- l ^Ri^V.

0,2

I R i - R 0^,8;

C 2   2_n I z dp

R + ®2 R z -     +

R ^{3 я} I ¹ p dR

R

1     д1

⁺ _p ^(T 0 ^R ( “ )

I i - k

I ^Ю д1 ^{( ю} я ) i J

X -0,2

V

R_i ^0,6 , k = 0,362

при

ддд

^{+ t} 0 R ( a )     ^t 0 R ( p )     ^t 0 R ( p )

® д1 <  ⁽ ® я ) i _1 , ^k = ^0,3018 при ® д1 >  ⁽ ® я ) i _1 .

Толщина потери импульса на втором диске:

окружные и радиальные напряжения трения от окружной и расходной составляющих скорости на

( 5 Д2 М⁵ : д2 )

|® д2 - ( ® я У ^R ' + ( CRlR i )

диске и на стенке:

– окружные напряжения трения на стенке [6]:

( 5 :; 2 )

( C     R )

' |®д2 "К ) , -J2 ^R + ( C R^f

П® Д2 - ^{( Ю} я ) i -1| k ^j--------------------¹

R_i 0,6

, k

0,362

при

^Ш д2 <  ( ^Ш я ) i -1 , k = ^0,3018 пРи ^Ш д2 >  ⁽ ® я ) i -1 .

Окружные напряжения трения и суммарные радиальные напряжения трения на дисках определяем по выражениям (1)–(4).

Новые значения на шаге интегрирования для угловой скорости ядра потока и статического давления в узлах R_i получим из выражений (11) и (12) соответственно при помощи модифицированного метода Эйле-

ра с пересчетом.

Следующий структурно-функциональный участок, который необходимо рассмотреть – торцевой зазор между вращающимся диском и неподвижной стенкой (рис. 1, полость B). Фактически, характер течения в этой полости определяет утечки из основного гидравлического тракта дискового насоса терния. Рассмотрим элементарный объем жидкости в торцевом зазоре между неподвижной стенкой и вращающимся диском (рис. 3). На рисунке т 0а , т Д _а - окружные на-

пряжения трения на стенке и на диске соответственно; T 0 R _а , т д R _а — радиальные напряжения трения от окружной составляющей скорости на стенке и на диске соответственно; т 0 _Кр , т Д _Rp - радиальные напряжения трения от расходной составляющей скорости на стенке и на диске соответственно. Элементарный объем представляет собой кольцо на текущем радиусе высотой dR ^ 0 и толщиной z 1 - нормальный зазор полости. Бесконечно малый элементарный объем делится на три участка: течение в ППС около неподвижной стенки, течение в ППС у вращающегося диска и течение в ядре потока. Течение на неподвижной стенке происходит в толщине пограничного слоя 5 _ст, где окружная скорость жидкости изменяется от 0 до U _я . Течение на вращающемся диске происходит в толщине пограничного слоя 5 _д, где окружная скорость жидкости изменяется от U _я до U _д – скорость вращения диска.

Для решения системы уравнений движения вязкой несжимаемой жидкости необходимо определить напряжения от расходного и вращательного течения жидкости [6].

Для полости между вращающимся диском и неподвижной стенкой проведем аналогичную процедуру, как и для полости между двумя вращающимися дисками. Путем интегрирования системы уравнений импульсов турбулентного (ППС), определяем

т 0 ^т _а = 0,01256 p® я R ²

**

^Ш я ^{R 5} а ст

V

\ -0,25

;

– окружные напряжения трения на диске [3]:

^{Т д} а = ^0,01256 р ( Ю д ^Ш я ) 2 X

х R ^г

Ъ -Ш я) R 5^

V

Поскольку радиальная составляющая напряжения трения формируется как окружным, так и расходным (радиальным) течением, то выражение для радиального напряжения на стенке имеет вид:

ст ст ст

^Т 0 R = ^Т 0 Rp ^{+ Т} 0 R а ;

– радиальное напряжение трения на диске:

д т0 R

дд

= ^Т 0 Rp ^{+ Т} 0 R а ;

– радиальные напряжения трения от окружной составляющей скорости на стенке:

ст           ст т0Rа ъст т0а ;

– радиальные напряжения трения от окружной составляющей скорости на диске:

дд

*0 R а     ^ъ д ^т 0а ^;

– радиальные напряжения трения от расходной составляющей скорости (определяются классическими соотношениями [4]) на стенке:

T 0Rp = 0,01256 р V rR

**

V R ⁵ аст

-0,25

V

;

– радиальные напряжения трения от расходной составляющей скорости на диске:

т д Rp = 0,01256 р V R¹

Vr 82

V

-0,25

.

Полученные напряжения трения позволяют интегрировать уравнения движения вязкой несжимаемой жидкости в заданных граничных условиях. При помощи этой системы дифференциальных уравнений, состоящей из уравнения движения вязкой несжимаемой жидкости в проекциях на цилиндрические оси

координат и уравнения неразрывности, можно решить задачу о течении в ядре потока. Для этого введем до-

пущения, аналогичные принятым при решении системы (5):

V dV R - U t = - 1 dp + 1 дт r ;

^R dR R р dR р д z ’

dU V U 1 дт я । r я _ а V Z? ।             —             ;

^R dR R р д z

dV V

—R + _R — 0

dR R

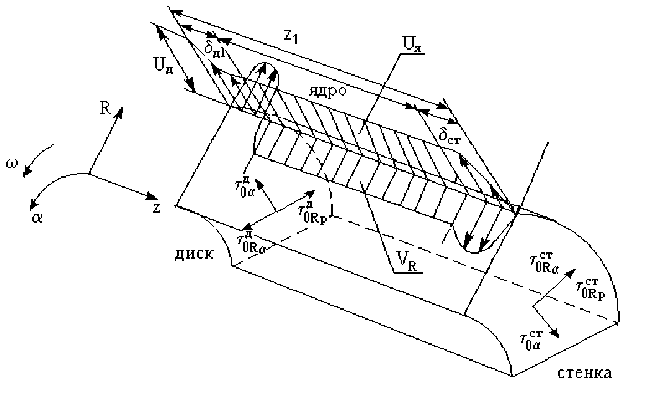
Рис. 3. Расчетная схема для полости между неподвижной стенкой и вращающимся диском

Проинтегрировав уравнения движения методами, аналогичными использованным при решении задачи течения между двумя вращающимися дисками, рассмотренными выше, и проведя соответствующие преобразования, получим (согласно расчетной схеме при течении от периферии к центру) дифференциальные уравнения для угловой скорости в ядре потока:

d ^Ю я _ ^2п ( д _— ст \ ^{2 ю} я dR р V ^{( 0 а 0 а)} R

Статического давления:

dp     ₂ р V ²

_ рю R +       + dR     я    4п2 n 02 R3

⁺ «0 ^{( Т д} R ( “ )

стдcт

^{+ Т} 0 R ( а ) ^{+ Т} 0 R ( р ) ^{+ Т} 0 R ( р )

Полученные выражения позволяют вести численное интегрирование и получить поле угловой скорости в ядре потока и поле статического давления, необходимые для оценки характера движения рабочего тела в полости между неподвижной стенкой и вращающимся диском.

Далее для определения напряжений трения необ-

ходимо вычислить толщины потери импульса на дис-

ке и неподвижной стенке. Толщина потери импульса

на диске определяется аналогично выражению Определим толщину потери импульса на стенке:

** ** ⁽ ® ^я ) i —1 ^Ri , I ®ст ) 1 ®ист ) 2 7 / , \2 ^{+ V 7} i ^{V 51} ( ю я ) 2—1 R ² + ( Cr/R )²

+

( ⁵ р ) ,

( Cr/R )²

( Ю я ) 2—1 R ² + ( Cr/R J²’

где (5“_ст) . _ 0,3018

^{( ю} я )

V

—0,2 ’ i —1

R_i 0,6

.

Компонента толщины потери импульса от расходной составляющей течения определяется по выражению (14).

Новые значения на шаге интегрирования для угловой скорости ядра потока и статического давления в узлах R_i получим из выражений (25) и (26) соответственно при помощи модифицированного метода Эйлера с пересчетом.

Таким образом, на основе выражений для напряжений трения выполнено интегрирование уравнений движения вязкой несжимаемой жидкости в граничных условиях торцевой щели и полости между двумя вращающимися дисками, которые являются основными участками гидравлического тракта дискового насоса трения, что позволяет при необходимой экспериментальной верификации разработать расчетную математическую модель дискового насоса.