Расчетное определение кавитационных характеристик центробежных насосов

Эти пузырьки содержат смесь пара и некон-денсирующихся газов. Когда пузырек проходит через области, где давление падает ниже давления насыщенных паров, они, как правило, резко увеличиваются в размерах. Область развитой кавитации состоит из большого числа этих пузырьков. При дальнейшем прохождении пузырьков по потоку, когда они попадают в область более высокого давления, происходит их схлопывание. Процесс схлопывания является сложным и зависит от многих факторов, таких как поверхностное натяжение, эффектов связанных с вязкостью и наличия неконденсирующихся составляющих в среде. Именно со значительными силами и давлениями, возникающими на последней стадии схлопывания, связана основная часть шума и повреждений, сопровождающих кавитацию.

Для получения расчетным способом срывной кавитационной характеристики H =f(Δ h ) разработчики программного комплекса Ansys CFX 12 предлагают использовать двухфазную модель. Кавитация при этом рассматривается как фазовый переход [1], однако использование двухфазных моделей, как правило, связано со значительным ростом вычислительных затрат. Также, как показала практика, подобные методики не всегда дают хорошую сходимость с экспериментальными даны-ми при расчётах кавитационных характеристик центробежных насосов.

В данной работе предлагается альтернативный путь прогнозирования кавитационных характеристик центробежных насосов, основанный с некоторыми допущениями на по-доб-ной методике, разработанной и используемой для определения антикавитационных качеств гидравлических турбин [2]. Суть методики состоит в следующем. Запишем выражение для гидравлического КПД РК насоса:

η Г ⁼

ρ ⋅ g ⋅ Q ⋅ H ω ⋅ M_Z

где М Z – крутящий момент относительно оси вращения рабочего колеса, ω – угловая частота вращения РК, Q – подача РК, H – напор РК, ρ – плотность перекачиваемой жидкости.

Из представленной формулы следует, что изменение напора РК на фиксированном режиме работы ( Q , ω=const) может происходить за счет комплекса η _Г ⋅ M _Z . Прогнозирование уменьшения напора более чем на 3% не имеет смысла, так как при развитой кавитации срыв работы центробежного РК происходит очень резко. Поэтому, если в представленном равенстве пренебречь изменением гидравлического КПД, то получим, прямую зависимость H от М Z . Величина момента М Z определяется по формуле:

MZ =∫Δp⋅r⋅dS S где Δp – перепад давлений на элементарной меридиональной проекции площадки dS поверхности лопасти.

Из представленной формулы видно, что за счет перераспределения давлений, величина момента M Z будет меняться. Современные программные продукты, в частности Ansys CFX 12 позволяют выполнить расчет пространственного течения вязкой жидкости в проточной части, по результатам которого есть возможность построить эпюры распределения давления вдоль контура лопасти в произвольном сечении. Пример такой эпюры представлен на рис. 1, где S – криволинейная координата меридианной проекции линии сечения лопасти от входной к выходной кромки, p - удельная энергия.

ρ ⋅ g

Пусть, например, при некотором значении Δh1 кавитация отсутствует и значение крутящего момента равно МZ1. Далее зададимся значением Δh2< Δh1. Эпюры давлений сместятся вниз на величину Δh=Δh1-Δh2. Будем считать, что на участке лопасти, где удельная энергия меньше удельной энергии соответствующей давлению парообразования, наличие кавитационной каверны как бы “срезает” бескавитационную эпюру давлений в зоне, где pp

< d и не сказывается на поле ρ ⋅ g  ρ⋅ g давлений на других участках поверхности лопасти и крутящий момент составил МZ2. В рамках указанных допущений можно по изложенной выше методике построить срывную характеристику H=f(Δh) и найти критическое значение кавитационного запаса ΔhКР, при котором произойдет снижение напора, например, на 3%.

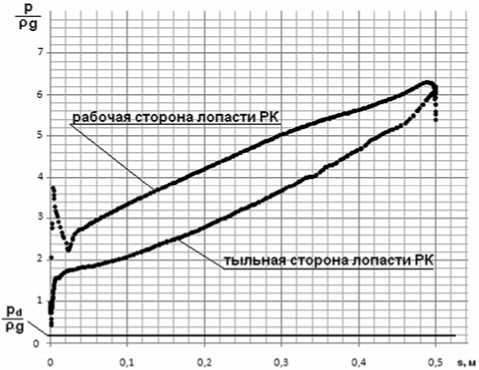
Рис. 1. Эпюра распределения давления вдоль контура лопасти в произвольном сечении

Для определения момента, действующего на лопасть РК целесообразно строить эпюру давлений в зависимости от меридианной длины линии сечения. При этом необходимо знать зависимость изменения радиуса от меридианной длины линии сечения. При изменении граничного условия – давления на входе в РК эпюра будет смещаться вдоль оси ординат на заданную величину. Если эпюра пересечет линию соответствующую давлению парообразования при данной температуре, то можно предполагать наличие кавитационных явлений в данном сечении лопасти. Для описанных методик определения кавитационных качеств насоса проведены верификационные расчетные исследования для центробежного колеса первой ступени питательного насоса с n S =83, С КР ≈1200 (при Q ≈250 м³/ч), отличительной особенностью которого является перерасширен-ная горловина и, как следствие, наличие противотока на входе на всех режимах. На выходе задавался массовый расход, соответствующий режимам, по которым имелись экспериментальные данные. На рис. 2-7 представлены результаты проведенных исследований для трех режимов работы РК.

Из представленных результатов можно видеть, что срывные характеристики, полученные на основе методики кафедры гидромашиностроения СПбГПУ [2], хорошо согласуются с экспериментальными данными до момента падения напора на ~ 4% (по результатам расчета течения с двухфазной моделью кавитации КПД РК в данном диапазоне практически не менялся). Что касается результатов, полученных по расчету с двухфазной моделью CFX, то они хорошо показывают момент полного срыва работы РК. Однако время, затраченное на построение срывной характеристики по результатам расчета с двухфазной моделью CFX, на порядок превышает время, необходимое для ее построения по методике [2].

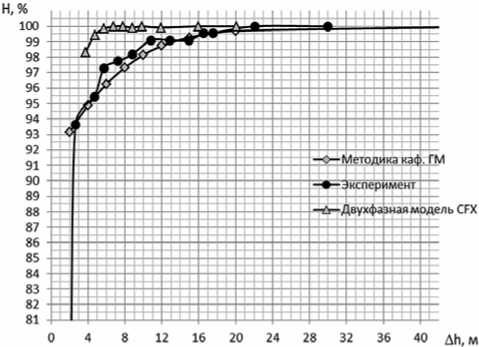
Рис. 4. Срывные кавитационные характеристики РК питательного насоса с n_S=83 ( Q =206 м³/ч)

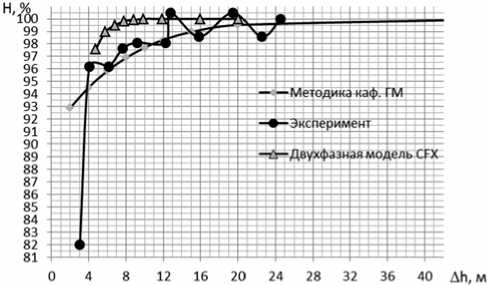
Рис. 2. Срывные кавитационные характеристики РК питательного насоса с n s =83 ( Q =253 м³/ч)

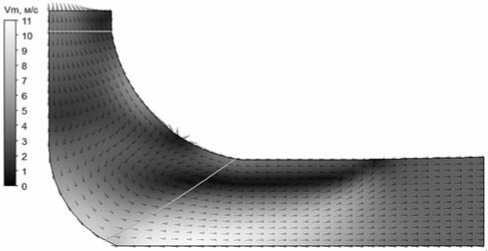
Рис. 5. Поле меридианных скоростей в консольном РК питательного насоса с n S =83 ( Q =206 м³/ч)

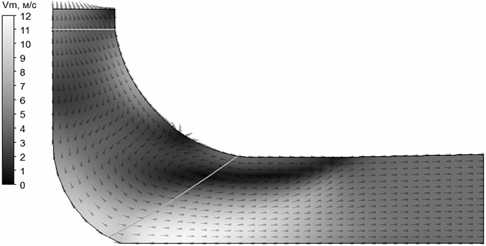
Рис. 3. Поле меридианных скоростей в консольном РК питательного насоса с n_S =83 ( Q =253 м³/ч)

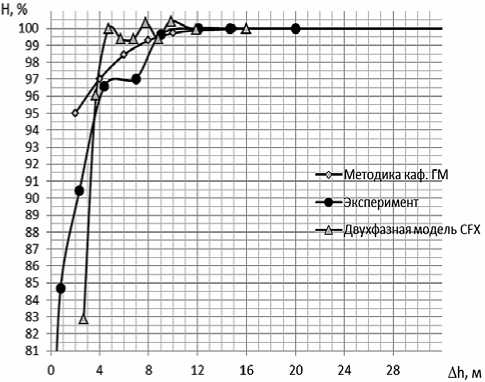
Рис. 6. Срывные кавитационные характеристики РК питательного насоса с n s =83 ( Q =94 м³/ч)

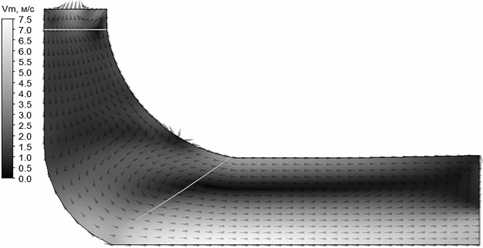
Рис. 7. Поле меридианных скоростей в консольном РК питательного насоса с n S =83 ( Q =94 м³/ч)