Расчетное прогнозирование технологических остаточных деформаций лопаток ГТД на этапе концевого фрезерования

циям фрезерования, в особенности это относится к производству маложестких деталей со сложным фасонным профилем, где наибольшее применение находят концевые фрезы. При этом нередко операции фрезерования являются окончательными операциями, на которых обеспечивается заданная геометрическая точность, шероховатость поверхности. При этом остаточные напряжения, сформированные на заключительных стадиях технологического процесса, оказывают большое влияние не только на усталостную прочность изделия, но и на ее геометрическую точность, поскольку являются основной причиной появления технологических остаточных деформаций [3], которые зачастую превышают технологические допуски.

В настоящей статье рассматривается влияние остаточных напряжений, сформированных на этапах концевого фрезерования на геометрическую точность лопатки компрессора газотурбинного двигателя семейства «НК». Для этого была использована методика [4], предназначенная для определения технологических остаточных деформаций в лопатке ГТД после операций ППД. Указанная методика реализована на лопатках ГТД, однако стоит отметить, что методика является обобщенной, применимой к деталям произвольной геометрической формы. Еще одной особенностью данной методики является то, что в конечно-элементной модели рассматривается не симуляция взаимодействия лопатки и упрочняющей среды, а используются в качестве исходных данных эпюры остаточных напряжений, полученные расчетным или экспериментальным путем. Таким образом, эпюра остаточных напряжений применяется в качестве исходных данных для моделирования напряженно-деформированного состояния поверхностного слоя конечно-элементной модели лопатки. Этот же подход был использован для операций концевого фрезерования в настоящем исследовании.

Таким образом, в соответствии с указанной методикой первоначально была разработана геометрическая модель лопатки компрессора ГТД семейства «НК» в программном комплексе SolidWorks (рис. 1), а затем уже разработанная виртуальная модель была экспортирована в программу конечно-элементного анализа ANSYS , для разработки конечно-элементной модели, вид которой представлен на рис. 2.

Конечно-элементная модель была разбита на два типа конечных элементов с четкой границей перехода, образующих основное тело лопатки и поверхностный слой, в котором на основе внесения соответствующих эпюр формируются остаточные напряжения. Следует отметить, что данный этап построения конечно-элементной модели сопровождался определенными трудностями, обусловленными, во-первых, незначительной толщиной поверхностного слоя, а, во-вторых, подбором оптимального типа конечных элементов. Выбранный тип конечных элементов должен был обеспечить возможность загрузки эпюр остаточных напряжений, предопределяющих напряженно-деформированное состояние лопатки. Поэтому, исходя из ранее изложенного, при построении конечно-элементной модели для разбиения поверхностного слоя были использованы элементы Solid-shell

• 190,    Solid-shell 181, Solid 95, а для основного тела лопатки – Solid 45. Примечательной особенностью элементов поверхностного слоя является то, что эти элементы могут быть поделены на заданное количество слоев, каждый из которых содержит точки интерполяции. Причем выбор количества слоев, на которые разбивается конечный элемент, зависит от количества точек, необходимых для построения эпюры остаточных напряжений.

С целью увеличения точности определения технологических остаточных деформаций в работах [4, 5] рекомендуется использовать начальные напряжения, получаемые расчетным путем из эпюры остаточных напряжений. Моделирование начальных напряжений позволяет реализовать в конечно-элементной модели процесс перераспределения начальных напряжений и образования остаточных напряжений и остаточных деформаций.

Согласно работам [4, 5] существует два способа определения начальных напряжений. Первый способ основан на решении интегрального уравнения, приведенного в работе [6]. Второй способ базируется на методе последовательных приближений [7]. Кроме того, что начальные напряжения возможно определить различными способами, их можно привести к различному виду, пригодному для загрузки в поверхностный слой конечно-элементной модели. На рис 3 приведена схема исходных данных, в виде остаточных и начальных напряжений пригодных для использования в конечно-элементной модели.

Как видно из рис 3 начальные напряжения можно приводить к упрощенному виду, а именно, к некоторой эквивалентной и постоянной по глубине слоя величине (Г _{э н}, которая может быть определена подходами [7, 8]. В работе использована методика, отличающаяся повышенной точностью и основанная на использовании

Рис. 1. Геометрическая модель газодинамической части лопатки компрессора ГТД семейства «НК», созданная в программном комплексе SolidWorks

Рис . 2 . Конечно-элементная модель газодинамической части лопатки компрессора ГТД семейства «НК», созданная в программном комплексе ANSYS

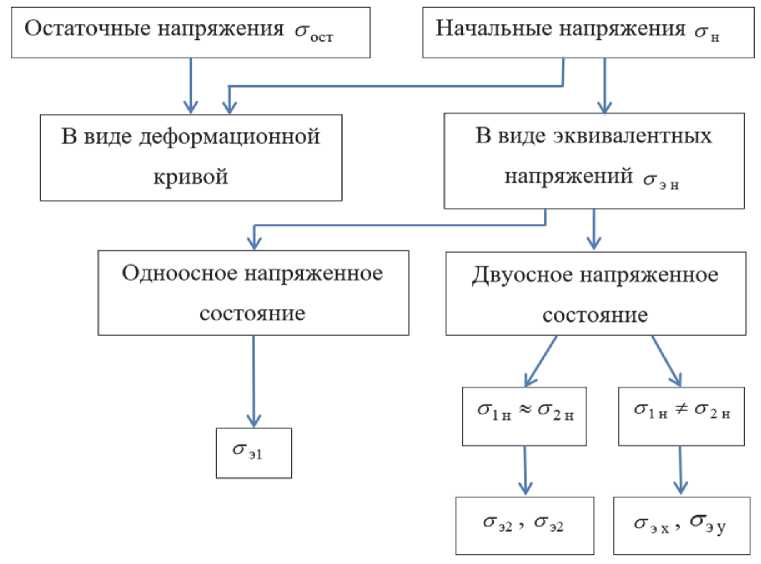
Рис. 3 . Схема выбора исходных данных для конечно-элементной модели исследуемого изделия (лопатки)

закона сохранения энергии, согласно которому энергия упругой деформации деталей U _д (т.е. энергия технологических остаточных напряжений [7]) связана с энергией поверхностного слоя U _а . Удельная энергия деформированного поверхностного слоя может быть определена из выражения, приведенного в работе [5]:

u о = ^"V7^+ ⁺ СТ ₂ ² _н + ^ - 2 Д ( ^ _1Н ^ _{2 н} + СТ 2_н ^ _3н + ^ н ^СТ 1 _н )] ,

2E где СТ1Н, СТ2 Н, СТ3 Н - главные начальные напряжения. Данное выражение также можно представить и в другом виде [7]:

u о =

^СТ Н

(1 — А ) • E ’

если СТ 3 _Н » 0 , а < 7 1_Н = СТ 2 _Н . В том случае, если в поверхностном слое детали начальные напряжения СТ 1_Н Ф СТ 2 _Н , эквивалентных величин СТ _{Э Н} будет две ( СТ _{Э х} , СТ _{Э у}). Получить выражения для их определения можно по алгоритму, представленному в работах [4, 5].

Согласно рекомендациям из трудов [3-5] детали, имеющие сложную фасонную форму, в число которых входят лопатки ГТД, должны анализироваться при использовании формулы, учитывающей двухосное напряженное состояние:

^СТ э2 =

1 Ч п „

^ ^{СТ н} d ^ a .

^{1 А} \ Ч с 0

В работе использовались эпюры остаточных напряжений, формируемые при концевом фрезеровании и полученные в результате проведе- ния численного полнофакторного эксперимента по разработанной методике [9]. Методика базируется на симуляционной конечно-элементной модели, позволяющей строить расчетные объемные эпюры остаточных напряжений (ОН) в поверхностном слое обрабатываемой заготовки. Конечно-элементная модель выполнена в постановке явной динамики, чаще всего обозначаемой в программах конечно-элементного анализа как «Explicit Dynamic» и имеет типовую структуру построения, а именно, содержит два виртуальных конечно-элементных тела разработанных в программе SolidWorks и экспортированных в ABAQUS, из которых первое тело это рабочая часть концевой фрезы, а второе обрабатываемая заготовка (рис. 4).

Для конечно-элементных тел были заданы исходные данные, необходимые для вычислений: физико-механические характеристики материалов, коэффициенты уравнения, описывающего пластическое поведение заготовки в процессе симуляции резания [10, 11], коэффициенты уравнения, описывающего процесс разрушения материала заготовки в зоне резания [11], кинематика виртуальных тел, соответствующая рассматриваемым в ходе численного эксперимента режимам обработки и результаты расчетов температурных полей. Данные полей температур соответствуют применяемым режимам обработки и определены с помощью методики, представленной в работе [12].

При проведении численного эксперимента определялись окружные остаточные напряжения. Варьируемыми параметрами режима

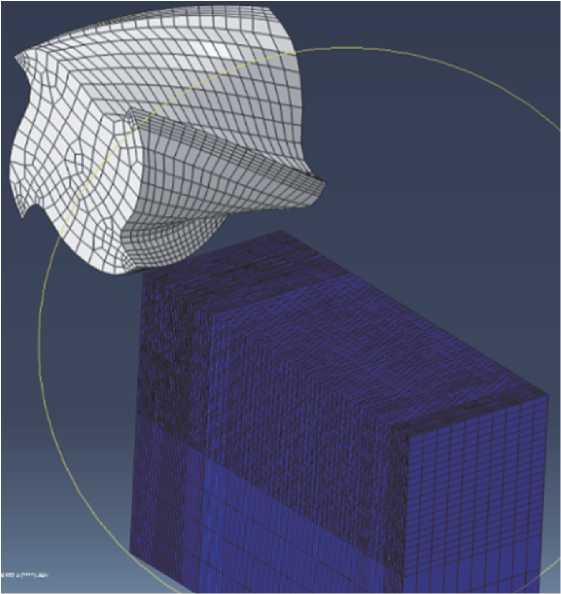
Рис. 4. Виртуальная конечно-элементная модель процесса концевого фрезерования

резания являлись: скорость резания U, подача на зуб Sz, глубина фрезерования t. Диапазоны варьирования указанных параметров были следующие: U = 23,8...37,7 м/мин, Sz = 0,04^0,08 мм/зуб, t = 0,5...1,5 мм. Пример симуляции процесса концевого фрезерования по разработан- ной конечно-элементной модели представлен на рис. 5.

Кроме того, с целью проверки адекватности методики для определения величины, знака и характера распределения остаточных напряжений по конечно-элементной модели, созданной

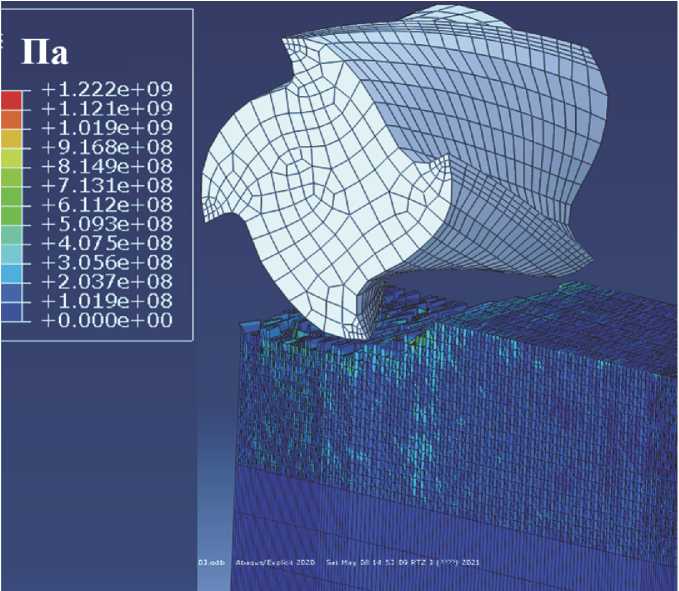
Режим резания: и = 30 м/мин; 5 _м = 250 мм/мин ( S z = 0,08 мм/зуб); t = 1,5 мм, B = 8 мм

Рис. 5. Конечно-элементная модель процесса резания для определения величины, знака и характера распределения ОН в программном комплексе ABAQUS, был проведен полнофакторный натурный эксперимент, при этом параметры режимов соответствовали режимам, использованным для численного эксперимента. Результат исследования сходимости численного и натурного полнофакторного эксперимента отражен в табл. 1. Пример распределения окружных остаточных напряжений по глубине поверхностного слоя заготовок обработанных в ходе натурного эксперимента представлен на рис. 6.

Проведенный натурный полнофакторный эксперимент позволил не только оценить точность разработанной методики, но и позволил получить степенную зависимость, связывающую величину максимальных окружных напряжений с параметрами режима обработки:

0,107 0,372

ст, - шс = 197,6 -и , S₇ ’ ^т o m /max ,           z

Как видно из данной формулы, она не содержит параметр t (глубину резания). Этот па- раметр был исключен на этапе проверки значимости коэффициентов регрессии.

Таким образом, в представленных исследованиях эпюры остаточных напряжений, соответствующие выбранным режимам концевого фрезерования и составляющие матрицу полнофакторного эксперимента, были использованы для определения начальных напряжений. Начальные напряжения моделировались в поверхностном слое конечно-элементной модели лопатки, после чего был выполнен расчет технологических остаточных деформаций. Лопатка была разделена на 7 контрольных сечений, каждое из которых соответствует контролируемому сечению реальной лопатки. И по результату расчета каждое сечение было проанализировано относительно его номинального положения. Деформации профиля в одном из сечений лопатки показаны на рис. 7.

Таким образом, с каждого контрольного сечения значения максимальных величин отклонений и поворота от номинального сечения были

Таблица 1. Результаты сходимости натурного и численного экспериментов (глубина фрезерования t = 1,5 мм.)

U , м/мин	S z , мм/зуб	ат - иао , МПа		А, %
		Натурный эксперимент	Численный расчет по модели
23,8	0.04	96,3	97,3	1.1
	0.06	107,2	120,8	12.7
	0.08	115	101,2	12
37.7	0.04	85	82,4	3.1
	0.06	110	107,7	2.1
	0.08	127,7	128,6	0.7

Таблица 2. Максимальные отклонения контрольных профилей пера лопатки от номинальных положений соответствующих профилей (глубина фрезерования t = 0,5 мм)

υ , м/мин	S z , мм/зуб	Максимальное смещение профиля от номинального положения, мкм
		Номера контрольных профилей сечений
		№1	№2	№3	№4	№5	№6	№7
23,8	0,04	2	37	71	140	210	279	311
	0,06	3	44	86	169	252	336	375
	0,08	2	33	63	125	186	247	276
37,7	0,04	2	26	50	97	145	193	216
	0,06	1	20	38	76	113	150	168
	0,08	2	35	68	134	200	267	298

Таблица 3. Максимальные величины поворота контрольных профилей пера лопатки относительно номинальных положений (глубина фрезерования t = 0,5 мм)

υ , м/мин	Sz , мм/зуб	Максимальный поворот профиля
		Номера контрольных профилей сечений
		№1	№2	№3	№4	№5	№6	№7
23,8	0,04	19’’	5’24’’	10’28’’	20’37’’	30’45’’	40’54’’	45’40’’
	0,06	19’’	5’10’’	10’1’’	19’44’’	29’27’’	39’10’’	43’43’’
	0,08	13’’	3’41’’	7’9’’	14’4’’	21’	27’55’’	31’10’’
37,7	0,04	10’’	2’51’’	5’31’’	10’52’’	16’13’’	21’33’’	24’4’’
	0,06	8’’	2’10’’	4’11’’	8’16’’	12’19’’	16’23’’	18’17’’
	0,08	14’’	3’57’’	7’40’’	15’6’’	22’31’’	29’57’’	33’26’’

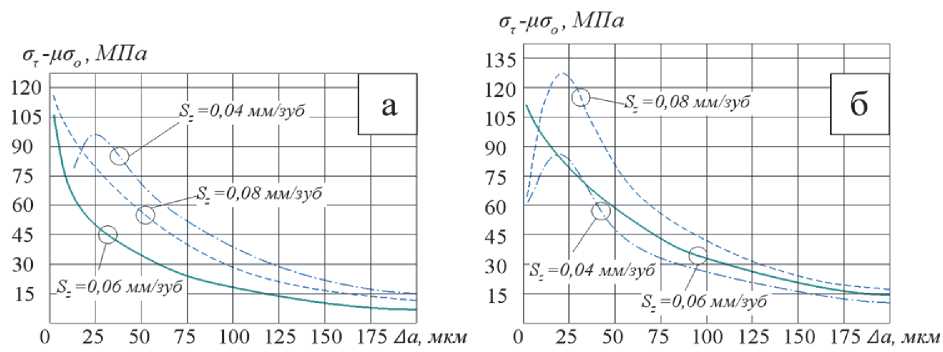
Глубина резания t = 1,5 мм

Рис. 6. Влияние подачи на зуб S при скоростях резания и = 23 8 м/мин (а) и U = 37,7 м/мин (б) на величину и характер распределения окружных остаточных напряжений при концевом фрезеровании

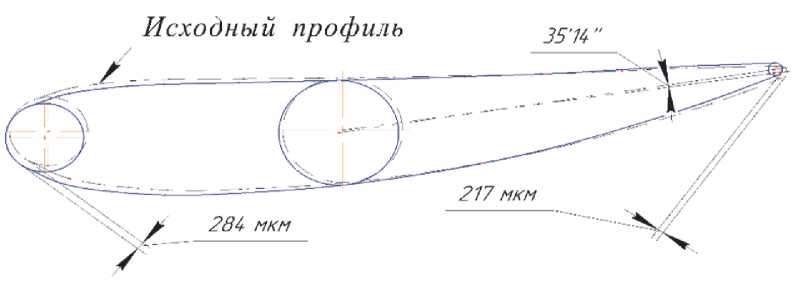
Рис . 7. Пример смещения деформированного профиля сечения №5 лопатки компрессора относительно номинального положения с указанием двух максимальных отклонений

занесены в таблицы. Пример для глубины фрезерования t = 0,5 мм представлен в табл. 2 и 3.

Исходя из полученных значений, возможно осуществлять подбор режимов фрезерования таким образом, чтобы остаточные деформации после обработки не вывели контрольные контура лопатки за пределы допуска. Для рассматриваемой в работе лопатке, по полученным в ходе численного данным, были составлены эмпирические зависимости, позволяющие определять для каждого из 7 сечений величину максимального отклонения контрольного контура в зависимости от параметров режима обработки (табл. 4).

ЗАКЛЮЧЕНИЕ

На основе проведенных исследований разработана методика, позволяющая прогнозировать технологические остаточные деформации лопаток ГТД, получаемые на этапах концевого фрезерования вследствие действия остаточных напряжений. Методика состоит из двух частей. Первая часть позволяет определить величины знака и характера распределения остаточных напряжений на этапах концевого фрезерования. Вторая часть содержит методику построения конечно-элементных моделей, алгоритмы аналитического определения начальных напряжений

Таблица 4. Эмпирические зависимости для определения максимальных величин смещения i -го контрольного профиля в зависимости от режима обработки

Номер контрольного профиля Эмпирическая зависимость Номер контрольного профиля Эмпирическая зависимость 1 о 0,146.0,277 Sz    t v1    '     ^0,219 5 s 0,18820,295 °5 = 8^5    у 0,275 2 с 0,175.0,287 Sz    t °2  144    у0,277 6 о 0,188.0,295 °б=1082 • -V0.26, 3 о 0,18.0,297 °. = 261     0,257 7 о 0,188.0,294 Szt °7  1224    у0,271 4 с 0,192.0,297 Sz    t ° 4   5 6 4      0,275 - - и задания исходного напряженного состояния поверхностного слоя на примере лопатки ГТД. Точность первой части методики была оценена в ходе сопоставления результатов, полученных численными методами с результатами натурного полнофакторного эксперимента, где расхождение между выходными данными не превысило 12,7%.

По разработанной методике проведен численный полнофакторный эксперимент, построены степенные зависимости, позволяющие определять величину максимальных отклонений контрольных сечений лопатки ГТД относительно их номинальных положений в зависимости от режима концевого фрезерования.