Расчеты стандартных энтальпий и энергий Гиббса образования карбидов хрома произвольного состава

В технической и теоретической термодинамике, наряду с теплоемкостью и энтропией, важнейшими характеристиками являются энтальпия и энергия Гиббса. В связи с этим необходимость создания математических моделей расчета стандартной энтальпии образования Д ^Я^ и стандартной энергии Гиббса образования AyG°98 бинарных веществ произвольного состава очевидна.

Несостоятельность моделей, в которых используется прямая аддитивность свойств компонентов или их инкрементов, обоснована в работах [1,2].

Любое бинарное соединение может быть представлено как АВ,. При стандартных условиях основной компонент А находится в кристаллическом состоянии, а компонент В - либо газ (О, N, Н, С1 и др.), либо кристалл (С, Si, Р, В и т.п.).

Для первого варианта разработана математическая модель расчета ДуЯ^, обоснованная согласием со справочными данными для оксидов [3, 4] и нитридов.

Во втором случае компонент В может сам выступать в роли кристаллообразующего, то есть -конкурента компонента А (металла). В связи с этим аналитические выражения модели отличаются от первого варианта. В качестве объектов изучения выбраны карбиды хрома.

Соединения СгС_х имеют большое практическое значение в металлургии, так как карбиды и карбонитриды (комплексные соединения на их основе) являются основными фазами-упрочнителями в сталях. Природа и свойства этих фаз во многом определяют их поведение в стали. Прочность связи между атомами металла и неметалла в соединении можно охарактеризовать стандартной энтальпией образования и свободной энергией Гиббса образования карбида, температурой плавления.

Диаграмма состояния Сг - С [5] показывает наличие трех прочных карбидов: Сг23С6 (содержащий 6,026 % (мае.) С), Сг7С3 (9,900 % (мае.) С) и Сг3С2 (15,400 % (мае.) С), имеющих температуру плавления 1520, 1780 и 1890 °C соответственно. По данным ряда исследователей [6] при температуре выше 2270 °C существует еще один карбид - СгС (18,765 % (мае.) С), разлагающийся при охлаждении на Сг3С2 и углерод, однако его существование экспериментально не подтверждено.

Температура начала восстановления оксида хрома углеродом до карбида равна ИЗО °C, а до элементарного хрома 1240 °C, поэтому при восстановлении оксида хрома углеродом невозможно избежать науглероживания сплава вследствие образования карбидов.

Карбид хрома Сг7С3 образуется чаще всего в конструкционных сталях с относительно невысоким содержание хрома (до 3-4 %). Этот карбид имеет сложную гексагональную решетку с 80 атомами на одну элементарную ячейку: 56 атомов металла и 24 атома углерода. Обычно такой карбид обозначают как (Сг, Fe)7C3 или Ме7С3.

Карбид Сг23С6 образуется в высоколегированных хромистых сталях при высоком содержании хрома (выше 5-8 %). Элементарная ячейка содержит 116 атомов: 92 атома металла и 24 атома углерода, выстроенных в сложную ГЦК решетку. В сталях данный карбид в чистом виде не встречается, а часть атомов металла замещается элементами, входящими в состав стали (Fe, Mo, W). В общем виде такой карбид в сталях принято обозначать формулой (Сг, Fe)23C6 или Ме23С6.

Карбид Сг7С2 - основная составляющая смеси карбидов (~96,4 %), образующихся при карбонизации смеси оксида хрома углеродом при высоких температурах в атмосфере водорода [6]; кристаллизуется в орторомбической системе.

Модель расчета стандартной энтальпии образования АуЯ°

С начала прошлого века предпринимались многочисленные попытки связать те или иные свойства веществ с зарядами ядер атомов. При этом были получены эмпирические уравнения для решения различных частных задач. Обычно в уравнение вводится «эффективный» заряд ядра -порядковый номер элемента с переменной, как правило, не обоснованной, произвольной поправкой. Так или иначе, все сводится к энергии (энтальпии) взаимодействия частиц. При этом не учитываются атомно-молекулярные связи, которые определяют пространственное расположение взаимодействующих частиц [7-9]. Именно они определяют кристаллические сингонии с характерными параметрами.

В работе [3] предложена математическая модель расчета энтальпии образования кристаллических оксидов, адекватность которой подтверждается экспериментальными (справочными) данными стехиометрических и нестехиометрических оксидов титана (22 оксида), созданы предпосылки для расчетов k^H других оксидов, нитридов, карбидов и иных бинарных соединений d-элементов.

Согласно предложенной модели энтальпия образования Ау/7(Л5_Л) выражается как удельная величина h (удельная энтальпия)

Коэффициент Zz равен сумме ядерных зарядов (порядковых номеров элементов) с учетом стехиометрического состава оксида:

£z = z(?i) + xz(S). (2) h - эффективная величина, так как принимается, что на каждый ядерный заряд приходится одинаковая доля энтальпии.

Зависимость h от состава можно отобразить линейным уравнением

Ъ = а+Кх, (3) где К - объемная структурная постоянная, включающая в себя линейные структурные постоянные и координационное число (к_Кч) кристаллообразующего вещества.

Все поле диаграммы «свойство-состав» разбивается на области твердых растворов, в каждой из которых выделяются кристаллообразующие (КО) компоненты. В первой ОТР кристаллообразующим всегда является металл (kjH =0 - по определению). В других ОТР в качестве КО может быть принят любой устойчивый оксид, для кото рого известны структура, состав, энтальпия образования, то есть h.

. Для любой системы зависимость h - х начинается с нуля (первая ОТР). Так как для каждой ОТР объемная структурная постоянная К имеет свое численное значение, определяемое сочетанием структурных констант веществ на границах ОТР, то координаты самих границ определяются совместным решением соответствующих уравнений (3) для областей. Во всех случаях kjH измеряется в кДжмоль*.

В ур. (3) К выражается в единицах удельной энтальпии h [кДж-моль"¹]. Коэффициент а определяется для каждой ОТР экстраполяцией зависимости h —х на х = 0, либо аналитически.

Анализ зависимостей С~^х-х и ДК~_п^х-х [10] показывает, что в системе Сг - С существует две ОТР, граница между которыми проходит через состав Сг₅С₂ (СгС₀,₄). Это соответствует переходу от кубических структур к более сложным (ГПУ и ромбической).

Для случая, когда свойство - это энтальпия образования, диаграмма так же должна содержать две ОТР с той же границей или близкой к ней. В табл. 1 приведены справочные значения [11-15] стандартных энтальпий образования для трех карбидов.

ОТР-1 (х = 0^0.4). КО - Сг

В этой ОТР по мере внедрения углерода происходит переход от структуры ОЦК (Сг) к струк-

Таблица 1

Зависимость энтальпии образования карбидов хрома СгС,от состава

⁼^оцк'^гпу "^Ккч =(V2-1)-4л/(Г4 = 16,2338 .

По определению эта область начинается с х = О, следовательно, ур. (3) упрощается:

й = 16,2338х.              (4)

Расчеты по ур. (4) приведены в табл. 1 и на

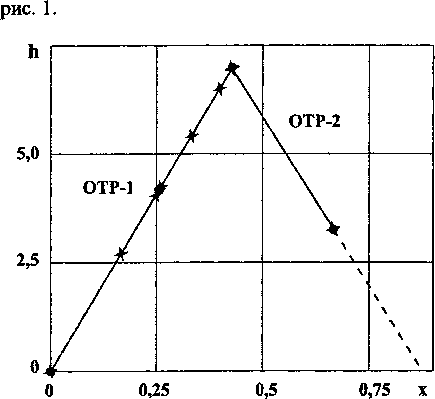
Рис. 1. Зависимость удельной энтальпии образования от состава карбидов хрома (• - эксперимент, х - расчет)

ОТР-2 (х = 0,4^0,66667). КО - Сг7С2

В этой области в качестве КО используем Сг₇С₃ как хорошо изученный. При переходе от структуры ГПУ ( к_ту = Зл/2 ) к ромбической ^к_ромб⁼ ~^ объемная структурная постоянная второй области К₂ = к_гпу ■ к_рт,_б ■ к_КЧ =

г

= 3V2---6 = 15,5885 (координационное число

^ККЧ~ 6).

Ур. (3) принимает вид:

h = a -15,5885 х.

Используя справочную величину Ду Я для соединения Сг₃С₂, располагающегося в ОТР-2 (h = 3,250±0,112), экстраполяцией на х = 0 определим значение коэффициента a = 13,6638.

Таким образом, для ОТР-2 ур. (3) окончательно примет следующий вид:

h = 13,6638-15,5885 х.       (5)

Расчеты по ур. (5) также представлены в табл. 1 и на рис. 1.

Совместное решение ур. (4) и (5), позволяет определить границу между областями ОТР-1 и

ОТР-2: х = 0,4294. Граница областей смещена в сторону большего содержания углерода - от соединения Сг₅С₂ к Сг₇С₃; различие между реальным составом карбида (СгСо,42857) и расчетным (СгС₀₁₄₂9₄) составляет 0,19 %. Средняя рассчитанная величина АуЯ(Сг₇С₃) = 185,208±0,342. Полученный результат согласуется со справочным, но доверительный интервал существенно сужен.

Модель расчета энтропии образования AyS0

В термодинамических расчетах большая роль отводится согласованию числовых значений величин. Одним из способов внутреннего (термические константы индивидуального вещества) и внешнего (термические константы различных веществ) согласований является использования свойств Р- потенциала.

Впервые понятие о Пи-потенциале Р и примеры использования его свойств было введено проф. А.Г. Рябухиным в 1977 г. [17]. По определению -это разность между стандартной энтропией образования и абсолютной энтропией вещества

P = kjS°-S°.

Отсюда стандартную энтропию образования можно выразить как

AyS°=P + S°.             (6)

Для простых веществ ур. (6) переходит в Р=-8°.

В последующих работах [18, 19] автором были проанализированы его свойства.

• 1.    Аддитивность (P-потенциал сложного вещества равен сумме P-потенциалов элементов с учетом стехиометрических коэффициентов)

• 2.    P-потенциал процесса равен нулю.

• 3.    P-потенциал не является функцией структуры, то есть не зависит от агрегатного состояния вещества.

Р(Р>4) = УР(Б) + ХР(Л) =

= -у8(В)-х5(Я).         (7)

Использование ур. (6) для определения AyS позволяет согласовать величины АуЯ и AyG данного вещества. Так как наиболее точно известны энтропии простых веществ (особенно газов), а величина P-потенциала не зависит от агрегатного состояния, то это позволяет рассчитывать AyS с точностью экспериментальных данных 8.                     ^:

Таким образом, предложенная методика может использоваться для согласования термических постоянных простых и сложных веществ независимо от их агрегатного состояния.

Результаты расчетов Пи-потенциалов карбидов хрома и их AyS приведены в табл. 2.

№	Вещество	AyG°, [12,13]	-Р, УР-(7)	S, [10]	AyS° УР-(6)	-kjH°, табл. 1	AzG	AyG°, УР-(8)
	1	2	3	4	5	6	7	8
1	С		5,740	5,740+0,126	0	0	0	0
2	Сг		23,603	23,603+0,209	0	0	0	0
3	Сг4С СгС0,25		100,152	105,426	5,274	103,491	4,1201	-105,063
4	Сг23С6 СгСо,26О87	-119,441	577,309	609,891+2,924	32,582	108,266	4,6114	-117,891
5	СГ5С2 СгСо,4		129,495	144,72+1,255	15,225	171,429	6,6654	-175,966
6	СГ7СЗ СгСо, 42857   '	-189,501	182,441	202,097	19,656	185,550	7,2035	-191,408
7	СГ3С2 CrC0j66667	-87,585	82,289	84,945+0,412	2,656	91,600	3,3000	-92,391
8	Сг6С СгСо, 16667		147,358	151,585	4,227	67,642	2,7561	-68,902
9	Сг3С СгС0;ззззз		76,549	83,151	6,602	140,691	5,4869	-42,658
10	СгС		29,343	37,463	8,12	-57,741	-1,8440	+55,321

Модель расчета стандартной энергии Гиббса образования A/G®

Энергия Гиббса (свободная энергая) AG является одной из важнейших термодинамических характеристик. Особая роль ей отводится в химической термодинамике, так как величина и знак AG позволяют судить о состоянии системы - о ее положении относительно равновесия. Изменение интенсивных параметров системы позволяет управлять химическими процессами.

Созданные математические модели расчета S, \jH позволяют определить A jG веществ, а С_р- температурные зависимости этих термодинамических характеристик.

В физической химии часто используется соотношение

AGr = А/7 - 7* AS.            ■

Применительно к стандартным условиям образования сложного вещества:

A/?⁰ = A_fH° - T_Q AyS°.      (8)

По этому уравнению с использованием полученных S и А ^Н рассчитаны A yG карбидов хрома, приведенные в табл. 2.

Совершенно естественно, что удельная энер-AyG гия Гиббса g = —-—, как и удельная энтальпия Sz

• h, образует две ОТР в функции состава х. Так как h(x), AS"¹^) внутри ОТР являются линейными

функциями состава, следовательно, и зависимость g(x) должна иметь аналогичный характер. В табл. 2 даны величины удельной энергии Гиббса g, а на рис. 2 представлена ее зависимость от состава g - х.

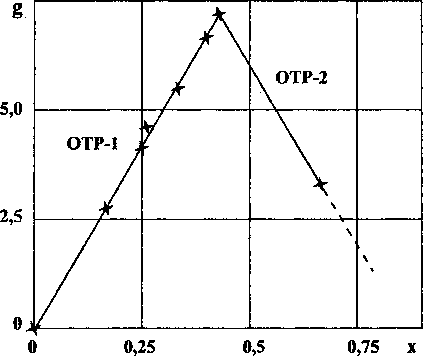
Рис. 2. Зависимость удельной энергии Гиббса от состава карбидов хрома (СгОх)

Расчетные точки ложатся на соответствующие пересекающиеся прямые. Однако в зависимости h-x во второй ОТР объемная структурная постоянная К имеет физическое обоснование. К как геометрическая величина не является функцией температуры. В зависимости g-x тангенс угла наклона, являясь комбинацией К_а(А-х) и

K_sTyES_in^l -xj , фактически представляет собой полуэмпирический коэффициент, так как включает температуру. Таким образом, для каждой температуры необходимо рассчитывать K_h - K_ST.

С другой стороны, если известно, что вещество, для которого имеется зависимость AyG, расположено в ОТР-1, то могут быть рассчитаны AyG для любых веществ, лежащих по составу в этой области. Важным следствием является линейная зависимость удельной энергии Гиббса от состава.

Выводы

• 1.    Разработаны математические модели расчетов стандартной энтальпии образования и стандартной энергии Гиббса образования для бинарных кристаллических соединений металлов с компонентами, являющимися кристаллическими в стандартных условиях (С, В, Si, Р, S, Ge, As, Sb, Bi и др.).

• 2.    Адекватность модели справочным данным подтверждена расчетами энтальпии и свободной энергии Гиббса карбидов хрома.

• 3.    Математические уравнения модели позволяют рассчитать стандартные величины энтальпии, энтропии и энергии Гиббса образования соединений произвольного состава

• 4.    Модель обладает предсказательностью. С помощью модели доказана невозможность образования карбида хрома СгС при стандартных условиях, так как расчетное значение AyG (СгС) = +55,321 кДж моль^-1 - величина положительная.