Расчёт аэродинамических характеристик возвращаемого блока ракеты-носителя типа «Союз-2-1а» при моделировании его возмущенного движения

Определение размеров районов падения отделяемых частей конструкции ракеты-носителя и их минимизация является важнейшей экологической проблемой [1], возникающей при проектировании ракетно-космических комплексов. Её решение выполняется путём моделирования динамики пространственного движения отделяемых частей на пассивном участке траектории. Следует отметить, что свободное движение в пространстве отработавшего блока после его отделения происходит под действием силы тяжести и аэродинамических сил, определяемых аэродинамическими коэффициентами. При модели-

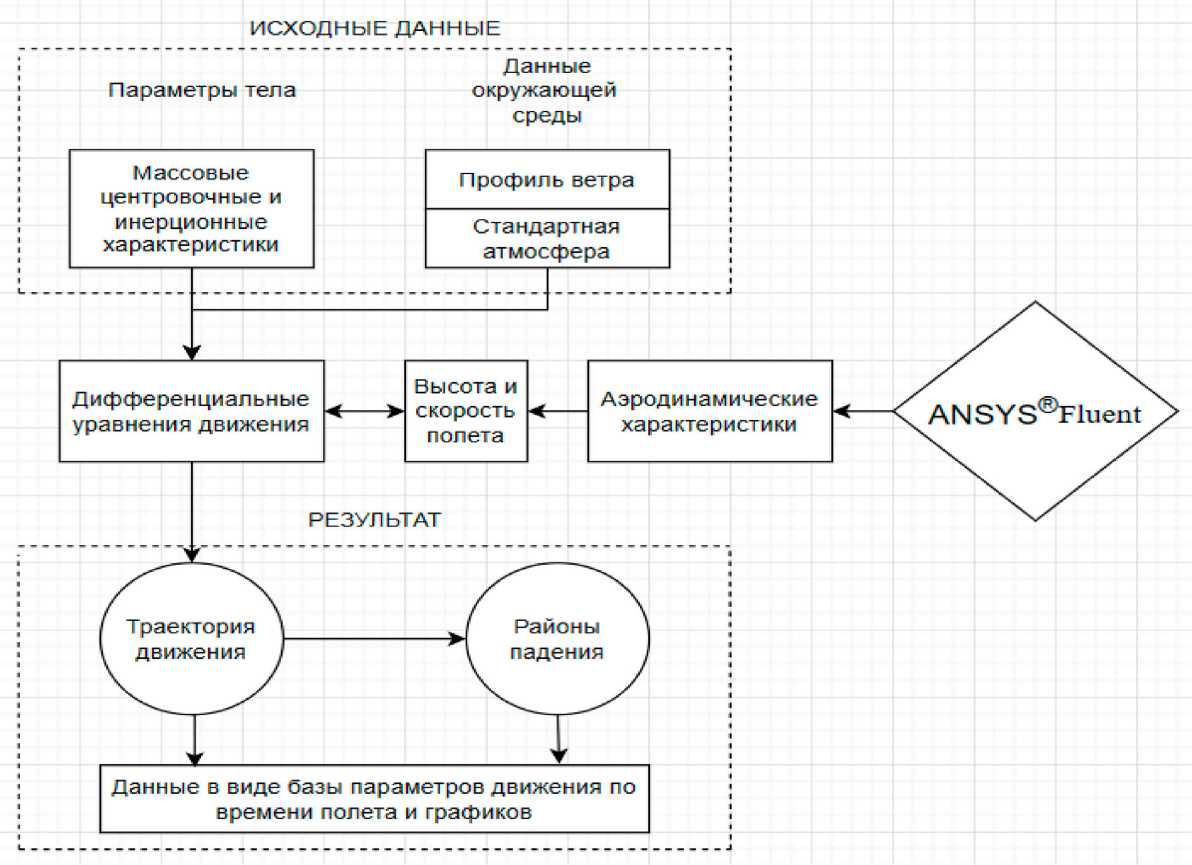
ровании пространственного движения возвращаемого блока ракеты-носителя, прототипом которого является центральный блок РН «Союз-2–1а», принят алгоритм, позволяющий рассчитывать аэродинамические коэффициенты на каждом шаге интегрирования. Он разделён на два блока: первый – непосредственно сам программный модуль интегрирования уравнений движения возвращаемого центрального упругого блока ракеты-носителя, второй – программный комплекс Ansys Workbench (включающий Fluent, CFX, Icepak, Polyflow), к которому на каждом шаге интегрирования обращается первый программный модуль. При этом решение задачи газодинамики выполняется методом конечных объёмов при помощи CAE-системы (системы компьютерного инженерного анализа) Ansys Fluent. Она включает в себя построение геометрической модели расчётной об- ласти, окружающей рассматриваемую конструкцию, разбиение расчётной области на конечные объёмы, а также построение физической модели, где указываются, например, подлежащие решению уравнения движения сплошной среды и граничные условия. Результаты расчёта представлены в виде графиков, характеризующих зависимости стационарных аэродинамических коэффициентов от угла атаки.

Общий расчет движения блока первой ступени выполняется с помощью известных моделей, параметрами которых являются данные, полученные в Ansys.

Текущие подходы к моделированию динамики отделяемых частей ракет-носителей, таких как центральный блок «Союз-2–1а», включают баллистические модели с упрощенными уравнениями движения и статическими аэродинамическими коэффициентами, интегрирование с шестью степенями свободы (6-DOF) для учета поступательного и вращательного движения, а также методы, интегрированные с вычислительной гидродинамикой, для расчета аэродинамики [2, 3]. Эти решения обеспечивают точность 80–95 % и используются для оптимизации зон падения, но часто полагаются на фиксированные коэффициенты из предварительных расчетов или экспериментов, что ограничивает учет нестационарных эффектов и упругих деформаций. Интеграция вычислительной гидродинамики с траекторным моделированием в реальном времени применяется редко из-за высокой вычислительной нагрузки.

Новизна предложенного алгоритма заключается в интеграции вычислительной гидродинамики с интегрированием уравнений движения в реальном времени, что позволяет динамически учитывать аэродинамические изменения на каждом шаге, повышая точность предсказания зон падения по сравнению с фиксированными коэффициентами. Кроме того, алгоритм включает учет упругих деформаций центрального блока через расчеты в Ansys Workbench, что добавляет полноту моделирования, отсутствующую в стандартных подходах с шестью степенями свободы. Модульная архитектура упрощает интеграцию с существующими моделями, делая метод более эффективным для экологической оптимизации. Эти особенности отличают алгоритм от текущих решений, где вычислительная гидродинамика обычно применяется в предварительных расчетах, и могут способствовать улучшению точности в предсказании траекторий.

1.    Математическая модель пространственного движения

На основе аэродинамических характеристик и параметров полета необходимо произвести моделирование движения центрального блока при помощи системы уравнения движения в проекциях на стартовую систему координат. Основной блок программы, рассчитывающий баллистическое движение, приведен ниже [2]:

'     dVx

m(t)    = —C_xqScos9cosQ — C_yqSsin9 + C_zqScos9sinQ — mgsin);

dVv

m(t) —^ = CxqSsin9cosQ + CyqScos9 — CzqSsin9sinQ — mgcos);

, . dV z                                        pW²

■

m(t) if = —C_xqSsinQ - C_zqScosQ — mgcos) — C_zS —

^ = К; ^ = К ; ^ = К; v2 = V2 + vy2 + V2;

dt x dt y  dt z x y z r2 = x2 + (R + y)2 + z2; h = r — R;

T = arctg n X ; 9 = arccos^; Q = arccos^; a = (p — 9, R + y           v           V где m – значение массы ракеты-носителя в текущий момент времени; q – скоростной напор, S – площадь миделя, V – абсолютная скорость ракеты-носителя; Vx и Vy – скорость ракеты-носителя в земной системе координат; X, Y – соответственно силы лобового сопротивления и подъемная сила ракеты; g – ускорение свободного падения; φ – угол тангажа, измеренный между продольной осью ракеты-носителя и горизонтом старта; φпр(t) – программное значение угла тангажа; α – угол атаки; x – дальность полета; y=h высота ракеты-носителя над поверхностью Земли; η – полярный угол; R = 6371 км – средний радиус земного шара; ϑ – угол наклона траектории, Ω – наклон орбиты, W – скорость ветра.

Ввиду осесимметричности конструкции коэффициент бокового сопротивления принимается равным коэффициенту подъемной силы.

Система уравнений доработана для трехмерного случая на основе [4].

Том 9

ANSYS®Fluent

Районы падения

Траектория движения

ИСХОДНЫЕ ДАННЫЕ

Данные в виде базы параметров движения по времени полета и графиков

РЕЗУЛЬТАТ

Аэродинамические характеристики

Параметры тела

Данные окружающей среды

Высота и скорость полета

Дифференциальные уравнения движения

Массовые центровочные и инерционные характеристики

Профиль ветра

Стандартная атмосфера

Рисунок 1. Общая блок-схема расчетного комплекса

2.    Построение расчётной области в Ansys

Для вычисления аэродинамических характеристик отделяемого блока ракеты-носителя в программе Fluent применяется связанная система координат, начало которой располагается в центре масс рассматриваемого блока (расположенном на расстоянии 11.55 м от нижнего среза корпуса блока). При этом ось x направляется вдоль оси блока в сторону верхней опоры, ось y – в сторону воздушного руля, а ось z проводится так, чтобы получилась правая система координат (рисунок 1). Влиянием фермы на аэродинамику блока прене-брегается.

Следует отметить, что в расчётах используются значения параметров стандартной атмосферы для высоты 40 км [5]: давление p = 287.143 Па; плотность ρ = 3.99566·10^–3 кг/м³; скорость звука a = 317.189 м/с; динамическая вязкость μ = 1.6009·10^–5 Па·с. Создание геометрической модели расчётной области выполняется средствами модуля проекта DesignModeler программного комплекса Ansys Workbench. При этом сначала строятся поверхности, описывающие внешнюю геометрию блока (рисунок 2). Они используются для определения объёма, занимаемого блоком.

Характеристики объекта исследования взяты из открытых источников [6].

Далее выполняется построение шара газообразной среды, окружающего блок, радиусом r _in 25 м и с центром в начале координат. И, наконец, на завершающем этапе выполняется булева операция вычитания (Subtract) объёма блока из шара. Построенному таким образом полому объёму присваивается имя «Rotating», и для него в качестве материала выбирается Fluid . Затем, собственно, для моделирования расчётной области газообразной среды генерируются цилиндр и полушар со сферическим вырезом. Как известно, для корректного задания граничных условий размеры расчётной области должны быть достаточно большими [1]. Учитывая этот факт, длина цилиндра принята равной 200 м, а радиусы цилиндра и полушара R = 120 м (рисунок 3). Радиус сферического выреза составляет r _out = 25.001 м, что на 1 мм больше r _in. Здесь угол атаки α выбирается в качестве проектного параметра, что позволяет легко изменять его значение.

Для данной расчётной области создаются следующие выборки (рисунок 3): «Inlet» – поверхность полушара и боковая поверхность цилиндра; «Outlet» – торцевая поверхность цилиндра; «CentralBlock» – внутренняя поверхность объёма «Rotating», представляющая блок; «Interface_ in» – внешняя поверхность объёма «Rotating»; «Interface_out» – поверхность сферического выреза в объёме «Fluid».

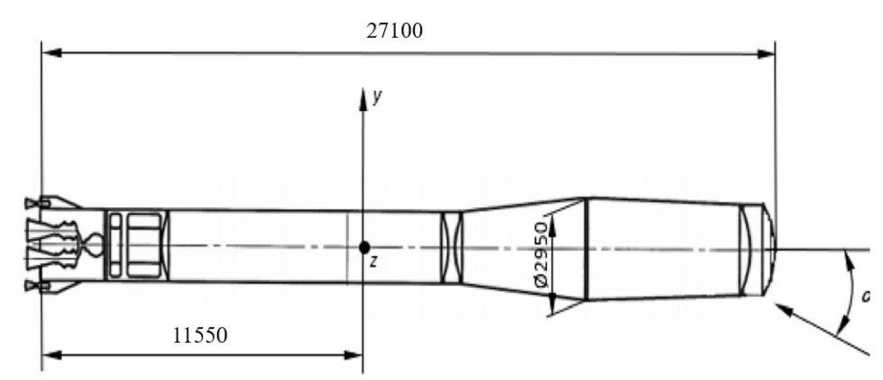
Рисунок 2. Эскиз блока и связанная система координат

Рисунок 3. Поверхности, моделирующие блок

Для определения параметров сетки на отдельных частях геометрической модели (рёбрах, гранях, объёмах) можно воспользоваться локальными настройками. В нашем случае для поверхностей из именованных выборок задаются следующие размеры расчётных ячеек: «CentralBlock» – 0,1 м; «Interface_in» – 1 м; «Interface_out» – 2 м. Построенная сетка представлена на рисунке 4, где для удобства изображения показано сечение плоскостью xy и сделана выноска, демонстрирующая слои расчётных ячеек, окружающие блок.

3.    Построение физической модели

Физическая модель определяется непосредственно в программе Fluent. При работе с данной программой прежде всего необходимо выбрать один из двух решателей. Решатель Pressure-Based подключает алгоритм расчёта уравнений Навье– Стокса, основанный на методе коррекции давле- ния. Решатель Density-Based базируется на решении уравнения для плотности, а давление вычисляется из уравнения состояния. Следует отметить, что первый разработан и традиционно используется для несжимаемых и слабо сжимаемых течений, а второй изначально был создан для высокоскоростных сжимаемых течений. В настоящее время оба подхода применимы для расчёта течений в широком диапазоне параметров, однако в некоторых ситуациях лучшие результаты обеспечивает первый, а в других – второй. В данной работе при расчёте аэродинамических характеристик блока для сравнения используются оба решателя.

Кроме того, нужно указать является ли задача стационарной Steady (то есть не зависящей от времени) или нестационарной Transient (когда расчётные величины зависят от времени). В нашем случае выбирается режим Steady .

Далее выполняется задание моделей физических процессов. На этом шаге необходимо ука-

Том 9

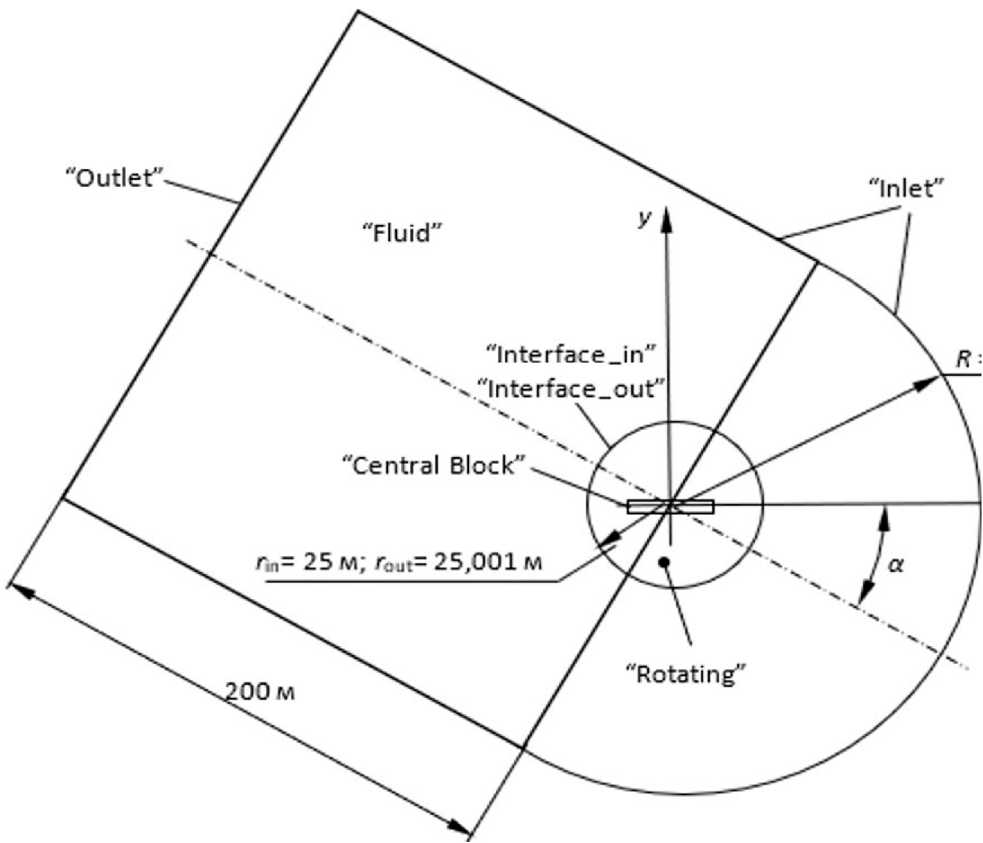
Рисунок 4. Расчётная область и именованные выборки

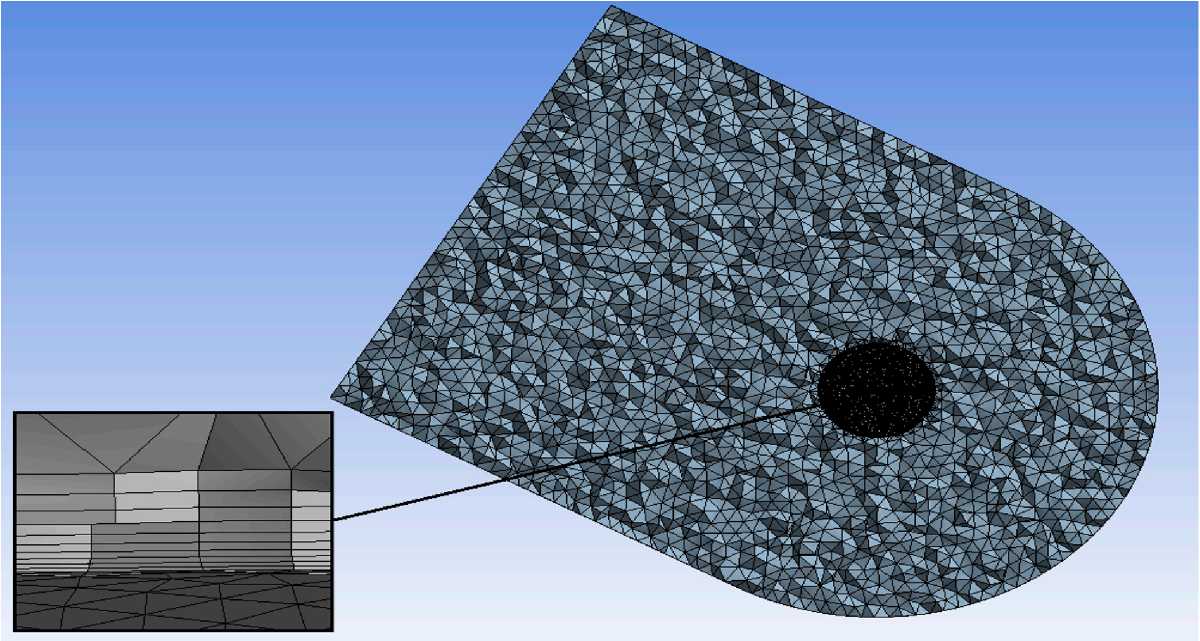
Рисунок 5. Разбивка на конечные объёмы

зать, какие уравнения движения сплошной среды будут решены. Исходная математическая модель всегда содержит уравнения законов сохранения массы и импульса. Все другие уравнения подключаются путём выбора их из списка моделей физических процессов, доступных в программе Fluent. Он включает в себя следующие опции: многофазность (Multiphase), тепловые эффекты (Energy), вязкость (Viscous), теплообмен излучением (Radiation), акустика (Acoustics) и т.п. Для рассматриваемой задачи обтекания блока необходимо задать лишь вязкость, которая позволяет определить способ моделирования турбулентности. В данной работе выбирается модель турбулентности SSTk- omega [3] с параметрами, задаваемыми по умолчанию.

Важным этапом подготовки расчётной модели является задание материалов и их физических свойств. Для расчётных областей «Fluid» и «Rotating», как отмечалось ранее, используется материал воздуха со значениями параметров стандартной атмосферы на высоте 40 км.

Затем задаются граничные условия. Они позволяют выделить единственное решение из множества всех решений дифференциальных уравнений, описывающих движение среды. Для этого необходимо определить значения искомых переменных на границах расчётной области. Граничные условия классифицируются в зависимости от их типа и того, какие газодинамические параметры заданы на границе. На входных и выходных границах программа Fluent позволяет использовать десять различных типов граничных условий.

В настоящей работе для определённых ранее именованных выборок (рисунок 3) назначаются следующие граничные условия:

• •    Для выборки «Inlet» устанавливается тип Velocity Inlet, предназначенный для задания скоростей и скаляров (температуры, концентрации компонента, турбулентных параметров и т.д.) на входных границах. При этом выбирается опция Magnitude and Direction, что позволяет раздельно задать абсолютную величину вектора скорости и его направление. Здесь число Маха м_∞ принимается равным 2 и, следовательно, величина скорости на высоте 40 км будет равна v_∞ = м_∞a = 634.378 м/с. Направление вектора скорости определяется путём задания направляющих косинусов: –cosα; sinα; 0 (где α – угол атаки). Кроме того, в качестве метода определения турбулентности выбирается опция Intensity and Viscosity Ratio (интенсивность турбулентности и отношение турбулентной и ламинарной вязкостей) со значениями по умолчанию.

• •    Для выборки «Outlet» устанавливается тип Pressure Outlet, используемый для задания статического давления и других скалярных величин на выходе. Это условие предпочтительнее других граничных условий на выходе и обеспечивает лучшую сходимость, если в процессе решения возникает возвратный поток [7]. В нашем случае избыточное давление (Gauge Pressure) полагается равным нулю, а турбулентность описывается точно так же, как и на входе.

• •    Для выборки «Central Block» по умолчанию задаётся тип Wall для определения неподвижной границы (стенки).

• •    Для выборок «Interface_in» и «Interface_out» выбирается тип Interface, который позволяет описать контактное взаимодействие на указанных границах.

4.    Результаты расчётов в Ansys

Отметим, что программа Fluent даёт возможность определить так называемые рабочие условия (Operating Conditions). Ненулевые рабочие условия для давления и/или плотности следует задавать, если изменения этих величин по сравнению с абсолютными значениями невелики, что позволяет предотвратить накопление ошибок окру- гления. В нашем случае здесь вводится значение атмосферного давления на высоте 40 км, равное 287.143 Па [5].

Как известно, если в модели присутствуют несколько тел, то требуется дополнительная сетка контактных элементов на поверхностях их взаимодействия. В нашем случае имеются два тела «Fluid» и «Rotating», которые взаимодействуют по контактным поверхностям, помещённым в выборки «Interface_in» и «Interface_out». Им предварительно был присвоен тип граничных условий Interface . Созданная для данных тел сетка является неконформной, то есть узлы на границах зон ²³¹ взаимодействия не совпадают. Поэтому здесь необходимо определить интерфейсы, указывающие, что соседние ячейки через эти границы передают информацию.

В заключение необходимо установить ещё и так называемые ссылочные значения (Reference Values), то есть значения отдельных физических величин (длины, скорости, плотности, давления и т.д.), которые используются на этапе просмотра результатов для вычисления безразмерных параметров, например аэродинамических коэффициентов. Ссылочные значения можно установить, исходя из данных на входе. Кроме того, здесь нужно задать характерную площадь и характерную длину. В настоящей работе в качестве характерной площади задаётся площадь миде-nd2„„ ля 5миД1 = —-—- = 6.83493 м2, а за характер- ную длину принимается длина блока без фермы L = 27.100 м (рисунок 1).

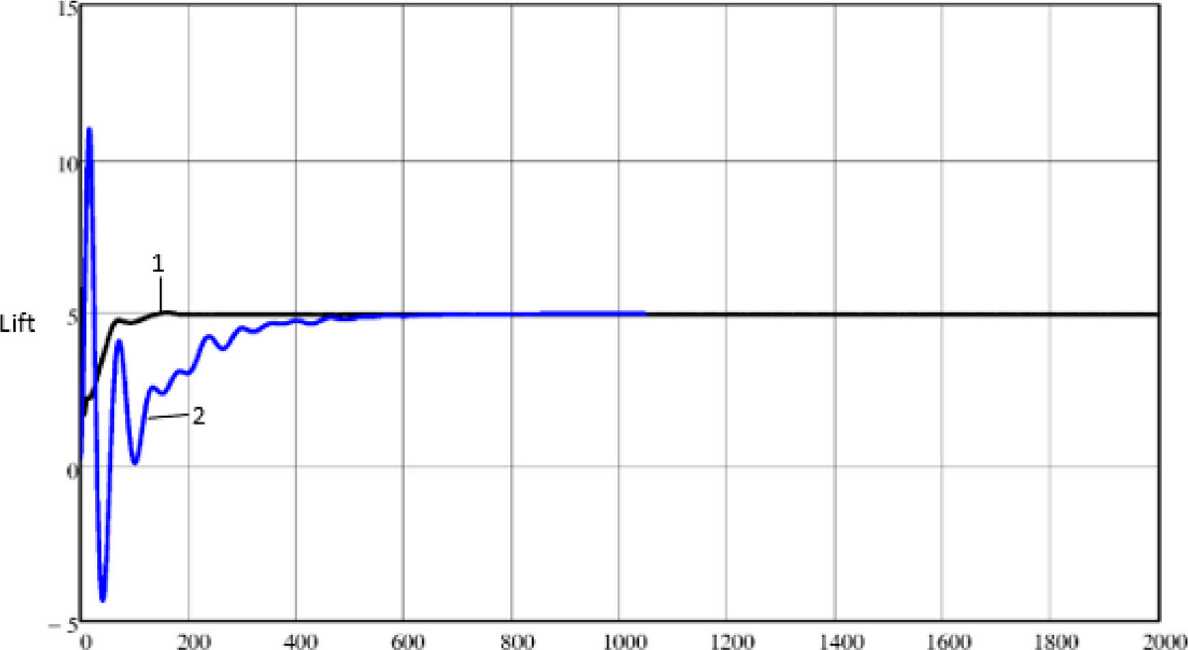
Как известно, решение стационарной задачи гидрогазодинамики в программе Fluent выполняется методом последовательных приближений (итераций). На рисунке 6 показаны зависимости коэффициента нормальной силы от числа итерации для одного из значений угла атаки (α = 120°), где меткой 1 обозначены кривые, полученные при использовании решателя Pressure-Based , а меткой 2 – кривые, рассчитанные на базе решателя Density-Based . Как видно, наблюдается достаточно хорошая сходимость и хорошее совпадение двух решений.

Далее в качестве примера представлены некоторые результаты для угла атаки α = 115°. Так, на рисунке 6 показано распределение скорости в плоскости xy . Видно, что максимальная скорость равна 1037 м/с, причём скорость невозмущённого потока составляет 634.378 м/с. На рисунке 7 изображено распределение давления по поверхности блока. Как видно, давление изменяется в пределах от минус 2068 до 911.5 Па.

I/ I — ОСМИЧЕСКИЕ АППАРАТЫ 1/1

Том 9

ТЕХНОЛОГА иен

Номер итерации

Рисунок 6. Сходимость по коэффициенту аэродинамической силы, действующей вдоль оси y

Рисунок 7. Поле скорости в плоскости xy

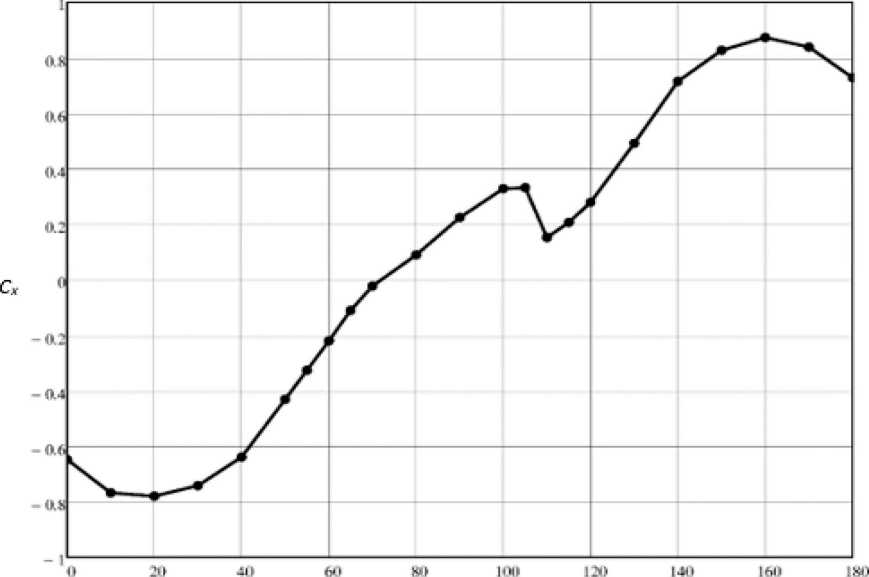
Основной целью настоящей работы является расчёт для блока аэродинамических коэффициентов продольной силы Cx, нормальной силы Cy и продольного момента mz для различных углов атаки α. Соответствующие графики приведены на рисунках 8–10. Следует отметить, что угол атаки α здесь варьировался в диапазоне от 0 до 180° с шагом 10°, а при резком изменении аэродинамических коэффициентов – с шагом 5°. Как видно из представленных рисунков, при угле атаки α = 60° коэффициент аэродинамической нормальной силы, а также коэффициент аэродинамическо- го продольного момента достигают максимальных значений. Кроме того, в районе угла α = 110° наблюдается резкое изменение коэффициента аэродинамической продольной силы.

5.    Результаты расчетов в баллистическом модуле

Согласно открытой трансляции полета РН «Союз-2–1а» с кораблем «С. П. Королев», проводимой ГК «Роскосмос» 18 марта 2022 года, центральный блок (прототипом которого является

Рисунок 8. Распределение давления по поверхности блока

«, град

Рисунок 9. Зависимость коэффициента продольной силы от угла атаки

объект исследования) отделяется в момент времени 287.7 с. РН в этот момент имеет скорость 3750, высоту 145 км и дальность 450 км [8]. На основании представленного алгоритма моделирования возмущенного движения были получены районы падения, учитывающие форму блока и условия обтекания его потоками воздушных масс с различными углами атаки (рисунки 13–15).

В таблице представлены данные для наклонения орбиты 98°. Расчетная программа на языке C++ с применением фреймворка Qt базируется на программе, применяемой в [9]. В расчетах учитывается сила ветра, направленная с востока вдоль оси z . В качестве стартовой площадки рассматривается космодром «Восточный».

If I— ОСМИЧЕСКИЕ АППАРАТЫ VI технологии ммн

Том 9

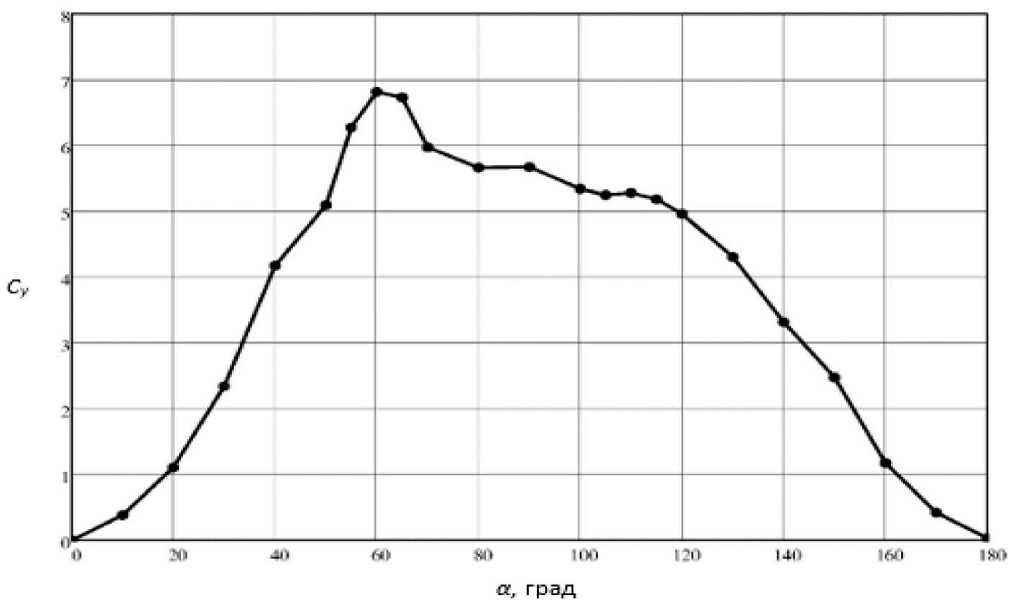
Рисунок 10. Зависимость коэффициента нормальной силы от угла атаки

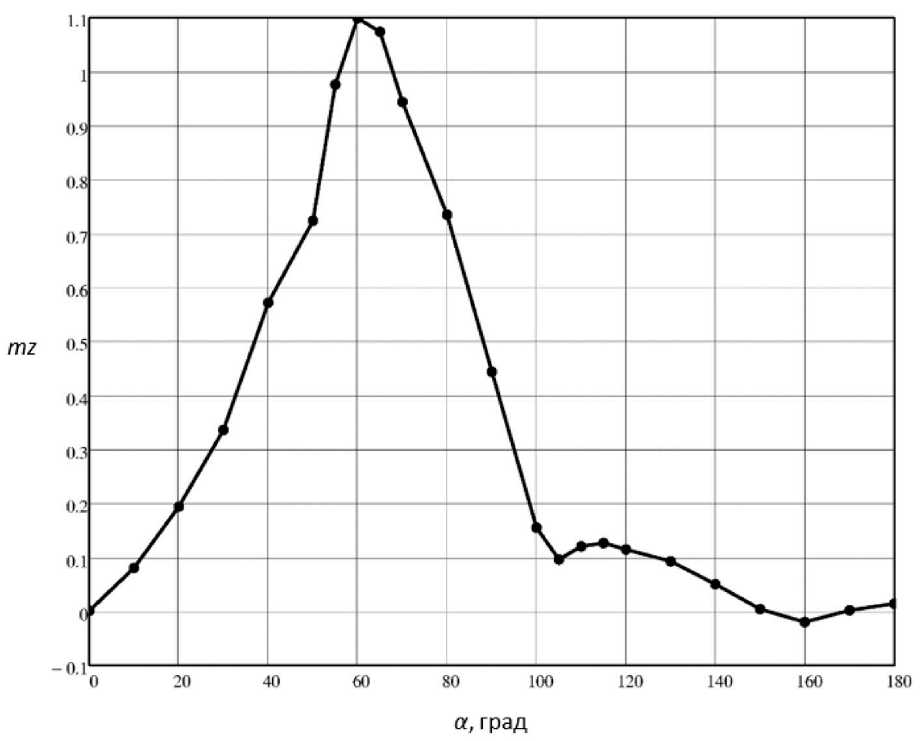
Рисунок 11. Зависимость коэффициента продольного момента от угла атаки

При формировании районов падения используются принимаемые в ракетостроительной практике отклонения блока (±75 км – продольное рассеивание, ±50 км – боковое рассеивание).

Заключение

Таким образом, представленная в данной статье методика решения задачи газодинамики для блока в неосесимметричной постановке даёт возможность рассчитывать возмущенное движение возвращаемого блока ракеты-носителя с учётом уточнённых аэродинамических коэффициентов на каждом шаге интегрирования для любых углов

атаки. Это напрямую связано с введённой в начале проблемой минимизации районов падения отделяемых частей ракет-носителей, таких как центральный блок РН «Союз-2–1а», и экологической оптимизации запусков. При использовании этих коэффициентов в качестве исходных данных расчёта можно получить траектории движения отработанного блока и определить координаты и районы падения, что повышает точность предсказания по сравнению с традиционными баллистическими моделями.

Задача о нахождении районов падения отделяемых частей является очень важной как для штатных ракет-носителей, так и для перспективных.

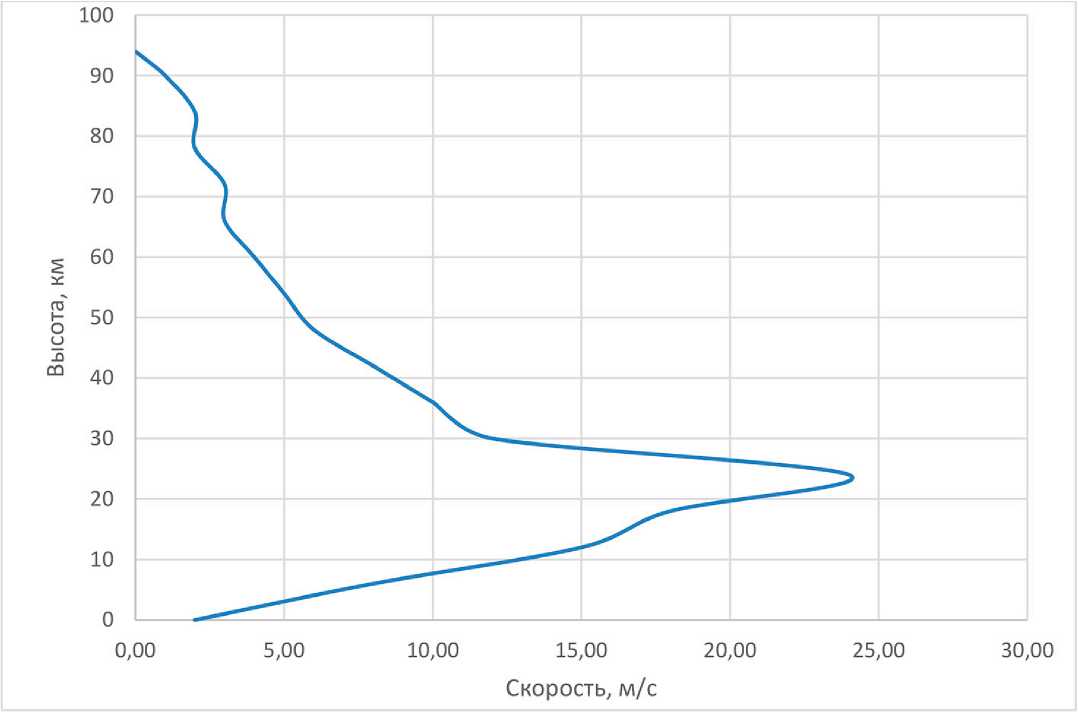
Рисунок 12. Зависимость скорости ветра на космодроме «Восточный» от высоты полета [10]

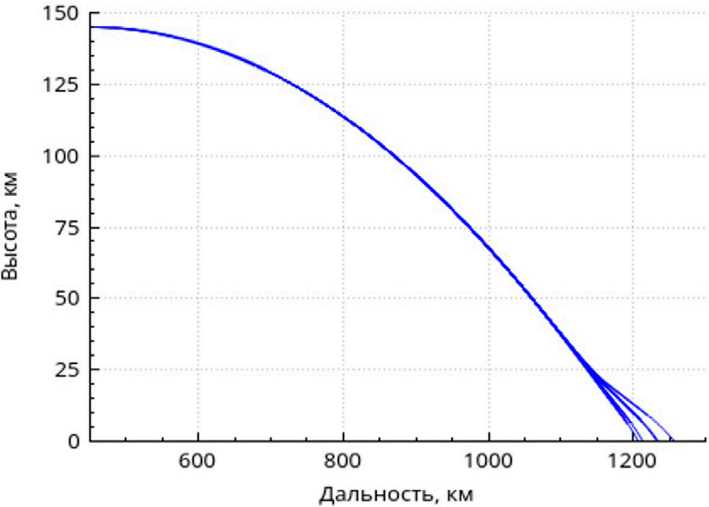
Рисунок 13. Траектория полета блока после отделения

Таблица

Результаты расчета дальности полета блока

α, град	0	20	40	60	80	100	120	140	160	180
х , км	1200	1213	1226	1243	1233	1225	1220	1204	1197	1195
z , км	2.818	2.573	1.747	0.506	1.119	1.188	1.365	1.903	2.461	2.759

Она особенно актуальна ввиду тенденций переноса всё большего количества запусков на космодром «Восточный» и необходимости определения районов падения в восточной части России [1]. Полученные результаты позволяют оценить предполагаемые места падения блока, чтобы учесть возможный вред для экологии и минимизировать воздействие на окружающую среду.

Приведённый в работе подход в дальнейшем позволит получить уточнённые траектории движения, в том числе с учётом упругости конструкции, что добавляет полноту моделированию и отличает его от существующих методов. Интеграция вычислительной гидродинамики с интегрированием уравнений движения в реальном времени открывает путь к более точному и экологически ответственному проектированию ракетно-космических систем, способствуя снижению зон падения и улучшению общей эффективности.

Том 9

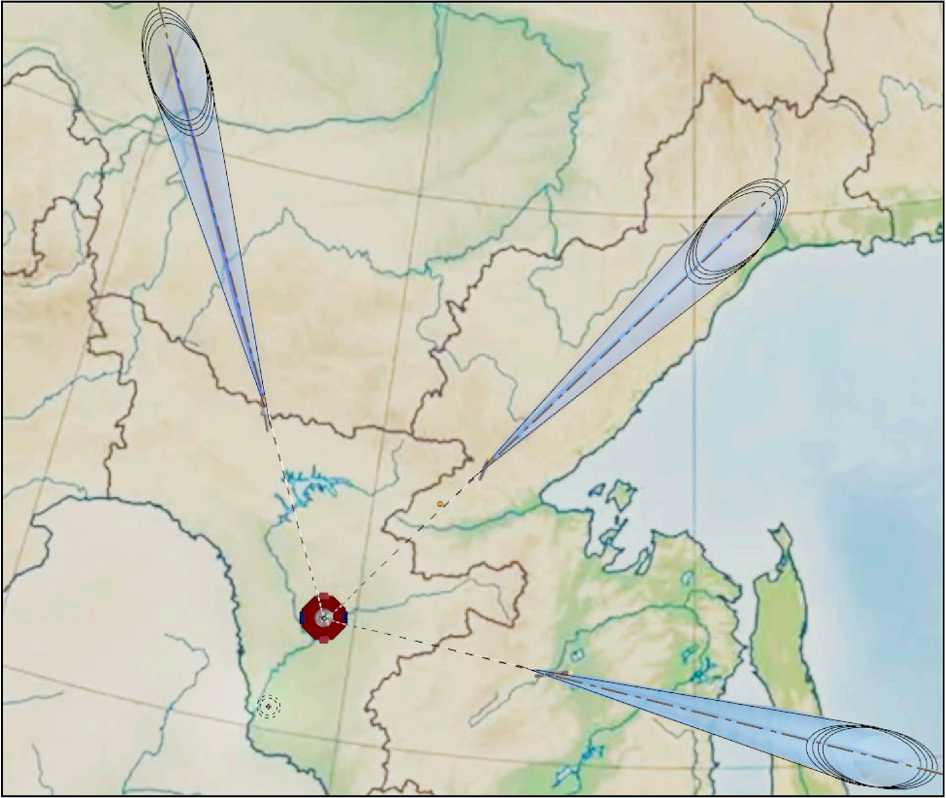
Рисунок 14. Рассчитанные районы падения для трех трасс полета (с наклонениями 51.7°, 64.8° и 98°) на примере запуска с космодрома «Восточный»

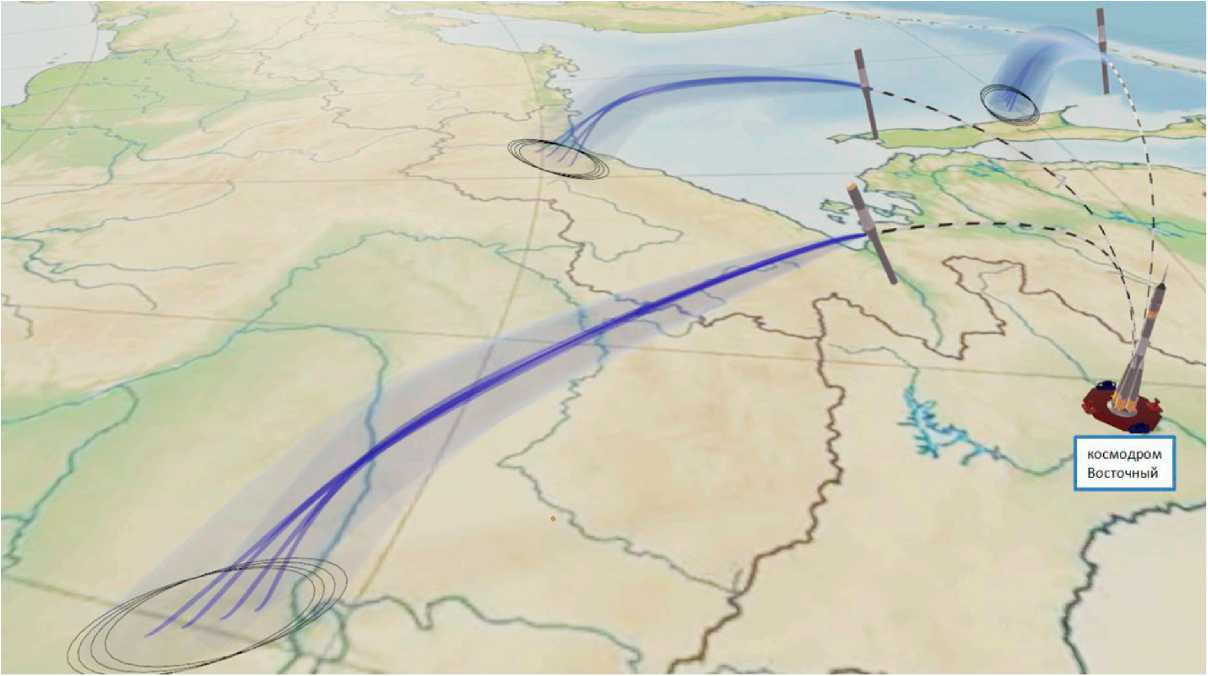
Рисунок 15. Траектории и районы падения в объемном представлении на карте Дальнего Востока (пунктиром показана траектория выведения, светлым – рассчитанная траектория падения блока)

Расчёт аэродинамических характеристик возвращаемого блока ракеты-носителя типа «Союз-2–1а»…

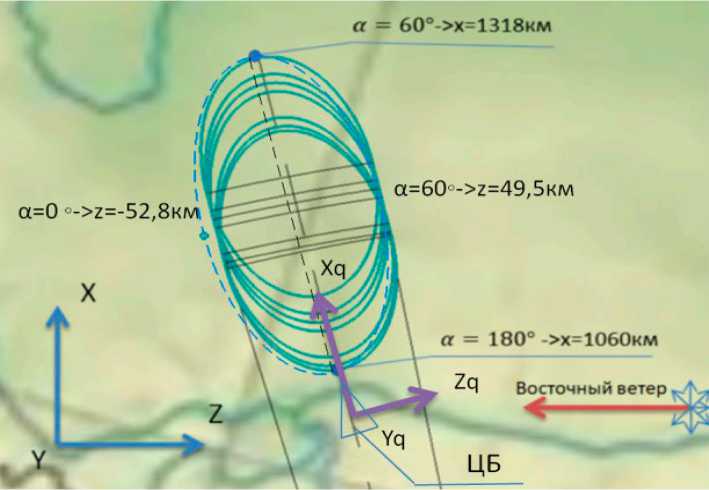
Рисунок 16. Габариты области расчетного района падения