Расчёт дифракции плоской волны на рассеивающем дробном аксиконе с учётом затухающих волн

В работе [1, 2] был определён и рассмотрен в рамках параксиальной модели новый дифракционный элемент, фаза которого описывается дробной степенью от радиальной координаты. Элемент был назван фраксиконом (дробным акси-коном). Если значение степени меньше единицы, то такой фраксикон в параксиальном приближении является рассеивающим и служит аналогом логарифмического аксикона [3].

Также ранее были рассмотрены [4, 5] рефракционные аналоги таких элементов в рамках геометрооптической модели. Эти элементы были названы обобщённой линзой, так как при конкретных параметрах можно получить такие классические элементы, как параболическая линза или аксикон.

Исследование фокусирующих свойств обобщённой линзы по сравнению с классическими оптическими элементами является актуальным для различных приложений [6-9], так как позволит заменить набор оптических элементов одним дифракционным элементом.

Действие оптических элементов в ближней и дальней зоне может очень существенно отличаться. В частности, фраксикон, степень которого меньше единицы, в дальней зоне дифракции является рассеивающим. В ближней зоне дифракции такой оптический элемент, аналогично ло-

Устинов Андрей Владимирович, ведущий программист.

гарифмическому аксикону [10], обладает фокусирующими свойствами.

В данной работе выполнен теоретический и численный анализ дифракции на дробном акси-коне, степень которого меньше единицы, в ближней зоне с учётом затухающих волн. При расчете было использовано преобразование интеграла Рэлея-Зоммерфельда первого типа.

1. ОСЕВОЕ РАСПРЕДЕЛЕНИЕ

ПРИ ДИФРАКЦИИ ОГРАНИЧЕННОЙ ПЛОСКОЙ ВОЛНЫ НА ДРОБНОМ

АКСИКОНЕ В НЕПАРАКСИАЛЬНОМ СКАЛЯРНОМ СЛУЧАЕ

Непараксиальная скалярная модель, основанная на теории Рэлея-Зоммерфельда [11], позволяет получать корректные результаты на очень близких расстояниях (всего несколько длин волн) от апертуры [12, 13]. Также в работах [14, 15] было показано качественное согласование результатов, полученных с помощью интегральных методов и конечно-разностных методов, с точностью до учета конкретной конфигурации оптического элемента.

Интегральное преобразование Рэлея-Зом-мер-фельда первого типа в декартовых координатах имеет следующий вид:

Л z / ^Xp( ik ¹ Ъ J

E ⁽ u , V , z ) = - — H E 0⁽ x , y )-------1 ik -- I d x d y , (1)

2я"            t V t )

^ 0

где E 0 ( x , y ) - входное поле, t = ^ ( u - x ) ² ₊ ( v - y ) ² + z , 5₀ - область, в которой задано входное поле, к = 2 л / X — волновое число, l - длина волны.

При рассмотрении поля на оптической оси (u=v=0) выражение (1) значительно упрощает- ся, и в условиях радиальной симметрии можно записать:

V ( ^r 0 ) = ( ^ka 0 ^r 0 )^{Y - k} V ^r 02 ^{+ z 2} ,          ⁽⁷⁾

то

E (0,0, z ) = - z J E _o( r )

exp ( ik^ r ² + z ² ) ( r ^{2 + z 2 )}

ik

-

1 )

I 2 , 2" I v r + z ;

r d r . (2)

Рассмотрим дифракцию плоской волны на дифракционном фраксиконе [1]:

т ( r ) = exp [- i ( ka_ar )^Y j, r <  R , (3) где a₀ - безразмерный коэффициент, связанный с числовой апертурой оптического элемента и определяющий степень фокусировки.

Для 0 <  y < 1 оптический элемент (3) на периферии имеет минимальное значение числовой апертуры, а в центре – максимальное. Значение параметра а 0 можно определить в соответствии с заданной минимальной числовой апертурой NA min на краю оптического элемента R :

а о =

^^ min ( kR ) ^{1 -Y} 1^?

Y

0 <  y < 1.

Если положить NA min =1 (предельное значение в воздухе), то элемент будет пропускать в основном затухающие волны, которые не распространяются вдоль оптической оси более чем на длину волны. В этом случае нужно детально рассматривать именно ближнюю зону дифракции.

При падении на фраксикон (3) плоской волны, ограниченной радиусом R, с единичной амплитудой, распределение на оси можно описать в приближении тонкого оптического элемента по формуле (2) при E 0 ( r ) = exp ( - i ( ka₀r )^Y ) . В работе [16] было получено представление (2):

E (0,0, z ) = exp( ikz ) -

z • exp

( ik T R ²

-

i ( k a₀ R ) ^Y )

R ²

+ z ²

-

V "( ^r 0 ) = ^-

k

V ^r 0 ^{+ z}

(1 - Y) + r0

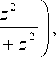
r 0 – стационарная точка, которая определяется из уравнения:

( ^ka 0 ) ^Y YT^{- - 1}

kr ₀

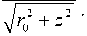
Выражение (6) достаточно удобно для численного расчета, но мало пригодно (по крайней мере, без дополнительных упрощений) для анализа зависимости комплексной амплитуды (или интенсивности) от расстояния и параметров фраксикона, так как в общем случае уравнение (9) не решается аналитически.

Далее проведём дополнительный анализ полученного решения для 0 <  у < 1 в ближней зоне дифракции.

2. ПОПРАВКИ В БЛИЖНЕЙ ЗОНЕ

Можно доказать [16], что при 0 <  у < 1 всегда имеется одна стационарная точка (максимум V ( r )) и нет точек перегиба: v "( r ) < 0 .

В отличие от r ₀ ( z ) , из (9) легко получается выражение обратной функции z ( r ₀ ) , поэтому рассмотрим её поведение.

z

k ^{2 - 2 Y} 2 2r

Y ^а 0 ^Y

_r ^{4 - 2} Y r ₀

^{- r} 0

.

Из (10) можно определить границу тени (т.е. правую границу существенных значений на оптической оси), соответствующую r ₀( z ) = R :

( kR ) ^{2 - 2 Y} _ ^z max      V Y²a ₀ ^{2 Y}

R exp

^- i Y ^{( k a} 0^{) Y z} • J----

r ² + z ²

-

i ( k a₀ r ) ^Y )

В окрестности точки максимума, соответствующей r ₀ = R , имеется приближённое равенство:

+ z ²

Y- 1 r ^Y

d r ,

которое удовлетворяет граничному условию при z=0 независимо от погрешности последующего вычисления оставшегося интеграла.

В работе [16] интеграл в (5) был приближенно вычислен модифицированным методом стационарной фазы [2]:

(M-2-2y          ira2-2- z2 (r0 ^R) = R2 \R^--11+2RI (R^-Y)-11(r0 - R).(12)

( r² a 0 ^Y ) ( r² a 2 ^Y          J ⁽ )

Отсюда имеем приближение для стационарной точки:

r

0max

R +

R 2 f ( kR )^{2-2 Y} l)

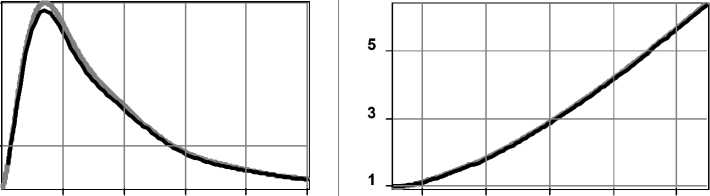
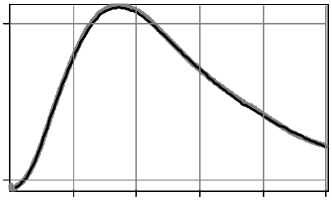
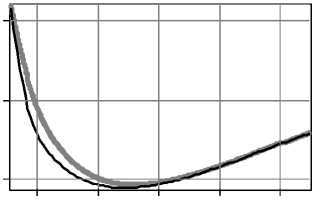
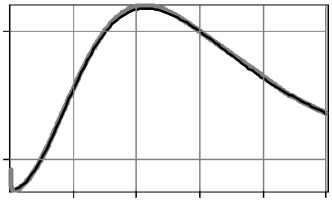
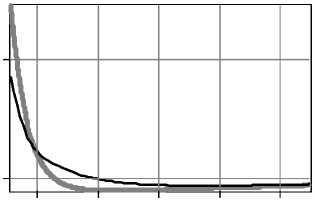
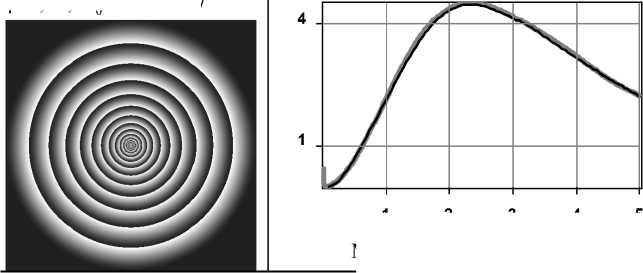
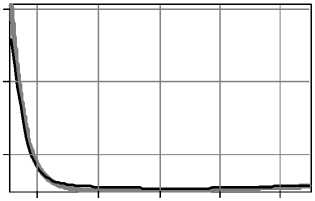
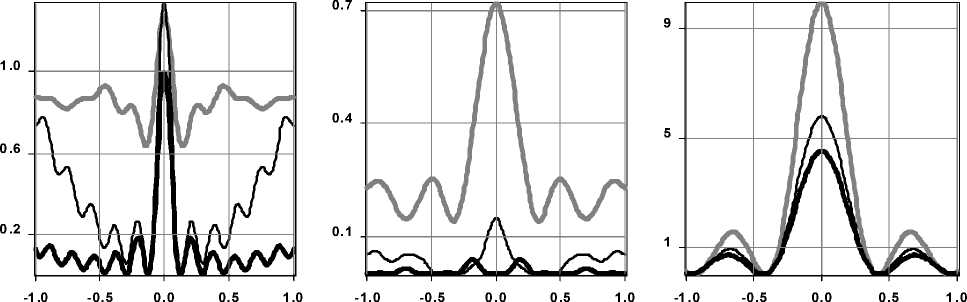
R 1 2   2 v v 2

V / ^a 0 J

2R

z• exp(ik^R²+ z²j

E(0,0, z) = exp(ikz) - exp (-i (kaR)^Y)----------- '            '        R²+ z²

f (kR )^{2 - 2 Y}

I 2 2r

V Y a 0^Y

(2 - у) -1

-

kr 2 ^t2

^-i^z M Axl¹Еi^V'^r0И I „/ it ) dt.

(r2+z2)    L      J^r(r0)' v 1

Зависимость в ближней зоне при z ^ 0 можно получить, рассмотрев окрестность точки

1/(2-2 -)

где t1 = -r₆ ^/рХгЗрз" , t2 = (R - r₆) ,y^"(r0)|72 ,

^{z 2}( ^r0 ^ rc )= ²rc^(1-Y) ( ^r0 ^-rc )

z²

^ r0 c = rc⁺^--— (14)

2(1- Y) rc

Так как при 0 < у< 1 интеграл (5) является несобственным, вклад окрестности начала координат может быть сопоставим с вкладом стационарной точки. Поэтому полученное в первом разделе общее решение (6) требует соответствующих поправок.

Вклад окрестности нуля с учётом осцилляций не превосходит площади нескольких первых лепестков. Оценим эту площадь. В центральной части (при r»0) фазовая функция (7):

V(r) = -kz + Р(ka₀r)^у,           (15)

Четверть периода (15) достигается при r = rq:

выпишем окончательный ответ, выраженный в исходной переменной r . Он, естественно, выражается разными формулами в зависимости от соотношения между z и rq . Ограничимся первыми двумя (при синусе) и тремя (при косинусе) лепестками: CIcor(z) = S 1^-(z) + S₂^-(z) + S₃^-(z) (граничные точки – значения, когда под знаком косинуса стоит 0, 90, 270, 450 градусов); SI_-o- (z) = SS (z) + SS₂ (z) + S2 (z) (граничные точки -значения, когда под знаком синуса стоит 0, 90, 180, 360 градусов).

Лепестки с косинусом, z< rq:

r

q

ka₀

Величина р мало отличается от единицы, поэтому далее её будем опускать. Таким образом, поправка равна величине

^brq exp (-i (ka₀r )^у)

Ecor^(z) = ^-iY^(k«.)^zexP(^ikz)• J-----1 2 2----

0 rr + z

S1- (z)=•	z H
	у(1 -у)

+------------+---------------r^у"¹

зу(Зу-1)rq^v(у-1)(Зу-1) q

14z  4

"T +^---Г, Y = 1/2, z3rq      rq

4,5 2,5 ln(rq/z)

z^2/3_r²'³      з_r²'³ ’ ^;,

0 < у < 1,

(20а)

r^{у 1}dr =.

= ^- i у( к «0)^уz exp (ikz )• EIcor⁽z).           (17)

S 2 ( z) =

{32-1/у 1 32-1/у 3 3З-1/у 1^

4------У 0 < у < 1,

2 у-1 у-1     Зу-1

_ 8/1ПЗ-1) _       у = 1/₂,        (20б)

Верхний предел в (17) равен нескольким rq . Из вида подынтегральной функции ясно, что поправка не будет пренебрежимо малой только при малых z. Способ приближённого вычисления интеграла следующий. Запишем его в тригонометрическом виде:

brq cos(ka,,rУ           brq sin(ka,,r)^у

EI-(z) = J'r-i Jr(18)

0 rr + z 0 W + z

С учётом последующего приближения делаем лепестки симметричными, что получается при замене r^y = y :

1 , cos(к«0) y ,1_f sin(к«0) y EI-or^(z) = - I  , „ , dy^- H , „ , dy, (19)

Vo Vy2/^у + z2 Vo Vy2/^у + z²

где f = (brq)^у.

Теперь интеграл стал собственным. Отрезок интегрирования разбивается по границам лепест-

ков, внутри каждого лепестка арка синусоиды заменяется аркой параболы (для этого и была нужна симметричность) из условия коллокации: совпадают нули и вершина арки. Знаменатель преобразуется следующим образом: он заменяется на z или на y 1/^у в зависимости от того, какая величина больше. Естественно, что лепестку, на котором происходит переход с одной замены на другую, будет соответствовать два интеграла. Из-за особого вида интеграла Jy^pdy при p = -1 ответ для у = 1/2 и у = 1/3 придётся получить отдельно.

Переписав (19) в виде

EI Ы = С1 UA-iSI (z), cor cor cor^,

4 -З1пЗ

0,704, у = 1/з, r_q

S- (z) =

r^{у-1 q}

'    <• 2-1/ у

8--

32-1/у   з 52-1/у

5 З2-1/у   5З-1/у

33-1/у

2у-1

у-1

Зу-1

•, 0 < у <1,

8(21п(5/З)-1)    0.17З

------;=-----=--, у = 1/2,

8/5-З1п(5/З) ^0,0675

2/З              2/З , ^у = ^1/З.

rr qq

Лепестки с косинусом, rq< z< З¹/^уrq:

----r^у, 0 < у < 1,

З уz q ,         ' ,

S1^- (z) = ^

3z

1/3

2r ^q

z

S- (z) = ^

(20в)

, у = 1/2,

, у = 1/3,

З z^у-1     2 z^2у-1 ( 2 1) z^Зу-1 ( 1       1 )

--1--I---I +--Г--------I---I

у^(1-у)    rq'  I 2у^-1  у)   rq¹ I ³у ³у^-1)

4 r^у           , , / 4        1        3

--r^у-1 •з^2-1/     ⁴--I, 0<у< 1,

Зуz ^q        (2у-1 у-1 Зу-11

z

8 rq 4 z

3z 3r_q

81п (З VrqTz)

у = 1/2,

1/3

1З,5 18 4,5   4r1'^{3   3}ln(^З(rq /^z) )

q

2/3            1/3      2/3                            2/3

z      (zrq )     rq       z            rq

(21а)

(21б)

S3c (z) совпадает с (20в).

Лепестки с синусом, z< rq:

z^2Y-1           z^3Y-1            4y-1           „      .

----------+----------—I-------------r^Y 1, 01 r,Y(2Y-1) 3Y(3Y-1)r2^Y (2Y-1)(3Y-1) q

SV z) = ^

+

3r ^q

r_q

, Y = 1/2,

(22а)

5 1 '2( z) = (

-r^{Y-1 q}

52(z)=(

Y -1

r' ^q

r^{2/3 +}'

1/3

r2/3

, Y = 1/3,

2^3-1/y_-2

23 - 1/Y

2 y- 1

3 y -1

, 0 < Y < 1,

4ln 2 - 2

0 773

-2"т=-, Y = 1/2,

3(1 - ln 2) _ 0,921

r_q2/3

r_q2/3

, Y = 1/3,

(22б)

'    4^1-1/Y _2^-1/Y

24--

^     2y-1

2.4^24/y_-2^14/y 4^34/y_-23^-1/y

Y-1

3Y-1

■, 01,

12ln2-8   0,316     ,

--=-^> Y=1/2,

(22в)

_ 333 4 ln2) 0 171

2/3             2/3 , * ^1/J.

rr qq

Лепестки с синусом, rq< z< 2¹/^Yrq:

SY(z)=	2 „ ---rY, 0< Y< 1, 3Yzq,             , 4r , Y = 1/2, 3 z
	2 r1/3
	, Y = 1/3,
	z

(23а)

52(z) = (

z^2Y-1(1    2 ) z^3Y-1( 1     1 )

1  1+I  I r* (Y 2*-1J r2^Y(3* 3y-1J

²rq_{+ r}Y-1 .₂3-1/Y fJL1 3yz q       ( 2y-1 3y-1J,

0 1,

2 4^q 4Tz 4ln(2y' z) F  3 z+ 3r+   Jr qqq

, Y=1/2

(23б)

2/3

_

2r^1/3

■ -q-+

z

1/3

^3ln(²r zг)

2/3

Y=1/3,

S2s (z) совпадает с (22в).

3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ И АНАЛИЗ НЕОБХОДИМОСТИ ПОПРАВОК

В БЛИЖНЕЙ ЗОНЕ.

Рассмотрим прямой расчёт (по квадратурным формулам) дифракции плоской волны в ближней зоне на фраксиконах с высокой числовой апертурой с использованием формулы (2).

Примем в (3) R = 52 и в (4) NAmin = 1. Тогда значение NA = 1 будет достигаться на краю оптического элемента, а в центре значение числовой апертуры будет выше и это означает необходимость учитывать при расчете затухающие волны.

По формуле (4) в принятых нами условиях параметр дробного аксикона оценивается следующим образом:

1-Y f 1 1Y а 0 =(10 л)* I-I , 0 <*< 1. (24) IY )

В табл. 1 приведены результаты дифракции ограниченного плоского пучка на дробном акси-коне при различных значениях *. Расчёты были выполнены двумя методами: на основе численного интегрирования выражения (2) с применением быстрого алгоритма расчёта, описанного в [17] и с использованием метода разложения по плоским волнам, реализованном для радиальносимметричных полей [14]. В последнем случае, при уменьшении расстояния от оптического элемента, необходимо учитывать всё больший диапазон пространственных частот, соответствующих затухающим волнам. При расчёте по формуле (2) этого делать не нужно, так как весь бесконечный диапазон пространственных частот уже учтён в подынтегральном выражении.

Как видно из табл. 1 два метода практически не различаются по результатам расчета на расстояниях более длины волны. Однако на очень близких расстояниях (z<0,12 ), где влияние затухающих волн очень велико, результаты несколько различаются. Данный факт отмечался также в работе [14].

Заметим также, что если рассматривать осевой участок z>0,5 2 (после ямы), то наблюдается поведение, аналогичное отмеченному ранее для фраксиконов большего размера [16]. А именно, максимумы и условная граница тени отодвигаются от элемента при уменьшении Y. Однако на начальном участке имеется принципиальное отличие дробного аксикона ( 0 < /< 1) от линейного аксикона ( / = 1): интенсивность не сразу начинает возрастать при увеличении расстояния, а вначале происходит убывание. Причём при Y, не близком к единице, этот минимум достаточно глубокий. Вычисление по модифицированному

Таблица 1. Результаты расчёта дифракции для дробного аксикона ( R = 5X ) с различными Y для NAmin = 1 на основе численного интегрирования выражения (2) (чёрный цвет линий на графиках) и с использованием метода разложения по плоским волнам (серый цвет линий на графиках)

Вид фазы элемента

Распределение интенсивности на оптической оси z е [0,1X, 5X] (z/X)

Распределение интенсивности на оптической оси z е [0,001X, 0,1X] (z/X)

Y=1, «о = 1

Максимум (z=0,7X) = 40

Минимум (z=0,001X)=1

0.01    0.03   0.05   0.07   0.09

Y=0,8, «0 = 3,125

Максимум (z=1,7X) = 10

0.9

0.7

0.5

Минимум (z=0,04X)=0,48

0.01   0.03   0.05   0.07   0.09

Y=0,5, «0 = 125,66

Максимум (z=2,15X) =5,8

1.0

0.1

0.01   0.03   0.05   0.07   0.09

Y=0,25, «0 = 7937607

Максимум (z=2,4X) = 4,5

-

методу стационарной фазы не предсказывает та кого эффекта, но результат может быть скоррек тирован при добавлении поправки (17).

Для проверки этой возможности выпишем в явном виде выражение (6) при малом z и добавим поправку (17):

E(0,0, z) = exp (ikz) -—exp Г ikR - i (k«₀R)^Y1 -R ^             ^

- ikz

. V (^Y-') I t2

1(2Г27р J ^exP (it²)^dt - i Y⁽k «0^)Y t

^z exp( ikz )• EIor⁽z).⁽²⁵⁾

Серый: минимум (z=0,034X)=0,01

Черный: минимум (z=0,065X)=0,044 1.0

0.6

0.2

Минимум (z=0,055X) = 0,018

0.01   0.03   0.05   0.07   0.09

Сравним слагаемые между собой.

Если R >X/(2л) , то второе слагаемое мало по сравнению с первым. Коэффициент

Ц =

2л

также невелик, так как в

знаменателе присутствует величина a₀ в положительной степени (например, при у = 1/2 ц = 4^/^^0 ), а в данном диапазоне а₀ велико. Кроме того, величина коэффициента завышена, так как в ней подставлено значение имеющегося в (25) ин-

теграла Френеля при бесконечных пределах.

Поэтому в первом приближении оставим только первое и последнее слагаемое:

E (0,0, z) = exp (ikz) [1 - i у( к a₀ )^Yz ■ EI_cor (z)] .(26а)

Так как общий фазовый множитель не влияет на интенсивность, его опустим:

• ^E, (0,0, z) = 1^-iу⁽ka₀^)Yz ■ EIcor⁽z).      ^(26б)

В силу громоздкости выражений для поправочного слагаемого, в общем виде анализировать (26б) не будем. Ограничимся частным значением / = 1/2 . Результаты численного моделирования (третья строка Табл. 1) показывают, что области z< 9rq, для которой имеются формулы, вполне достаточно для выяснения, необходимы ли поправки.

Если воспользоваться формулами из предыдущего пункта, подставить в них значение rq = л²/(4ка₀) и ввести для удобства переменную 5 = 2 ^к а₀z / л , то получим следующее кусочнонепрерывное выражение для амплитуды поля:

1+л(5²ln5-0,1145²-53/3) +

E1(0,0,5) = -

+л(-5+1,1545²- 53 / 3), 0 <5<1 1+л(0,585²+ 5²ln(5/2)-5³ /з) +

+л(1/3 - 35 -0,0435²- 25²ln(5 /3) + 5³ /з) ,1 < 5< 2

Анализируя это выражение, можно показать, что интенсивность имеет минимум, равный

1,12л² . . . . 0,0478 при 5 = 2,117 , т.е. при z =------= 0,0152 .

ка₀

Этот результат получается средним между двумя вариантами, полученными численными методами. В случае прямого расчета по формуле (2) получается очень близкое значение минимума, а при использовании метода разложения по плоским волнам оказывается более точное положение минимума.

Оно, с учётом его некоторой грубости, вполне согласуется с результатами численного моделирования, особенно при использовании разложения по плоским волнам. По глубине минимума согласие лучше, чем по его положению. Кроме приближённости аналитических формул здесь сказывается и то обстоятельство, что дно минимума очень пологое (см. третий столбец таблицы).

Таким образом, доказано, что корректный расчет в зоне затухающих волн возможен только при учете поправочного слагаемого (17), так как без него минимум, во всяком случае, такой глубокий, обнаружить невозможно.

Поперечное распределение интенсивности в ближней зоне дифракции, рассчитанное на основе метода разложения по плоским волнам для рассмотренных выше оптических элементов, приведено на рис. 1.

Как видно, в плоскости максимальной интенсивности размер центрального светового пятна примерно одинаковый во всех случаях и равен по полуспаду от максимального значения: FWHM=0,385 X для /=0,8, FWHM=0,395X для / =0,5 и FWHM=0,4X для / =0,25. Однако с уменьшением параметра g уменьшается интенсивность светового пятна.

Выигрыш использования рассеивающего дробного аксикона с /<1 проявляется только на очень близких к оптическому элементу расстояниях. В частности, на расстоянии z=0,01 X размер центрального светового пятна равен FWHM=0,266 X для /=0,8, FWHM=0,123X для / =0,5 и FWHM=0,118l для / =0,25. В этом случае световое пятно оказывается в 5 раз меньше дифракционный предел.

Таким образом, численно показано, что с помощью рассеивающего дробного аксикона, степень которого значительно меньше единицы, в зоне затухающих волн формируется светового

• (а)                                      (б)                                        (в)

Рис. 1. Распределение интенсивности на расстоянии (а) z=0,01 X , (б) z=0,1 X и (в) в плоскости максимума интенсивности для / =0,8 (серая линия), / =0,5 (тонкая черная линия), / =0,25 (толстая черная линия)

пятно, имеющее как продольный, так и поперечный размер порядка одной десятой длины волны. Однако данный результат получен в скалярной теории дифракции и соответствует лишь одной компоненте электрического поля.

ЗАКЛЮЧЕНИЕ

Для анализа дифракции плоской волны на дробном аксиконе, степень которого меньше единицы, использовано преобразование интеграла Рэлея-Зоммерфельда первого типа, позволяющее учитывать влияние затухающих волн в непосредственной близости от оптического элемента.

Применение метода стационарной фазы для оценки распределения комплексной амплитуды на оптической оси оказалось недостаточно точным. Для качественного согласования теоретических и численных результатов необходимо учитывать поправочные слагаемые.

Численный расчет на основе интеграла Рэлея-Зоммерфельда и с использованием метода разложения по плоским волнам показал, что дробные аксиконы с У <1 и имеющие высокую числовую апертуру в плоскости максимальной интенсивности формируют центральное светового пятна примерно одинакового размера (FWHM=0,39 X )• Однако с уменьшением параметра У уменьшается интенсивность светового пятна. Это связано с тем, что элементы в этом случае становятся более высокоапертурными, и основная энергия идет в затухающие волны.

В ближней зоне (в непосредственной близости от оптического элемента) дробный аксикон, степень которого значительно меньше единицы, позволяет формировать световое пятно, имеющее как продольный, так и поперечный размер порядка одной десятой длины волны. Заметим, что данный результат получен в скалярной теории дифракции и соответствует лишь одной компоненте электрического поля. Для получения полной картины дифракции необходимо учитывать векторный характер электромагнитного поля. Тем не менее, данный результат может быть полезен при взаимодействии излучения с веществами или материалами, чувствительными к определенным компонентам электромагнитного поля.

Работа выполнена при финансовой поддержке гранта РФФИ 13-07-97004-р_поволжье_а.