Расчёт двухрядного шарикового подшипника, нагруженного усилиями и моментом

В опоре автомата перекоса несущего винта, а также в опоре рулевого винта вертолета установлены двухрядные шариковые подшипники.

Общие виды узлов, в которых установлены подшипники, показаны на рис. 1 и 2.

Подшипники собираются с преднатягом за счет подшлифовки торцов внутренних колец. При этом контролируется момент сопротивления вращению подшипника.

По техническим требованиям в рабочих условиях подшипники нагружается осевым и радиальным усилиями и опрокидывающим моментом. В этой связи при разработке методики расчета подшипника следует предусмотреть осевую, радиальную и моментную нагрузки как в [1].

Двухрядные радиально-упорные подшипники работают при небольших скоростях вращения. Однако при осевой нагрузке происходит разгрузка одного из рядов, и тогда нагрузки и углы контактов шариков в этом ряду будут определяться центробежными силами. В связи с этим при расчетах подшипников целесообразно учитывать центробежные силы шариков.

Общий вид подшипника в сборе приведен на рисунке 3. Оба ряда подшипника имеют одинаковые номинальные размеры. Однако с учетом допускаемых отклонений углы контакта шариков и смещения колец при затяжке можно определять расчетом каждого ряда.

Величину начального угла контакта определим по формуле:

а о = arccos ( 1 - g/2R m ) .

Здесь g – радиальный зазор в подшипнико, а величина R _m определяется по формуле

R m = R в + R н - D w , в которой D w - диаметр шарика, R в и R н – радиусы желобов внутреннего и наружного колец.

При перекосе колец возможно выкатывание шариков на кромку замка наружного или внутреннего кольца. Угол контакта шарика с кромкой замка определится по формуле:

а з _Н = arccos ( 1 - ( D _H - D 3 )/ 2 R _H ) ^- для наружного кольца;

а _3в = arccos ( 1 - ( d ₃ - d _в )/ 2 R _в ) - для внутреннего кольца.

Здесь: d в и D н – диаметры по дну желоба внутреннего и наружного колец; d_з и D з - диаметры замка на противобазовых торцах внутреннего и наружного колец.

В связи со значительным изменением величин углов контакта шариков с кольцами следует учитывать при расчете подшипника изменение радиусов кривизны в контактах. При расчетах по компьютерным программам удобно пользоваться зависимостями, приведенными в работе [2].

При предварительной затяжке внутренних колец все шарики загружаются равномерно и углы контакта с внутренним и наружным кольцами будут одинаковыми. При этом силовые и геометрические соотношения для отдельного шарика без учета деформаций колец при посадке будут определяться для каждого ряда, как показано на рис. 4.

При недостаточной величине усилия предварительной затяжки в рабочих условиях под действием осевой нагрузки возможна полная разгрузка одного ряда шариков. В этом случае второй ряд шариков будет нагружаться только внешней осевой нагрузкой подшипника.

По техническим условиям при сборке подшипника необходимо обеспечить заданный момент сопротивления вращению. Контроль осуществляется по моменту трения на наружном кольце.

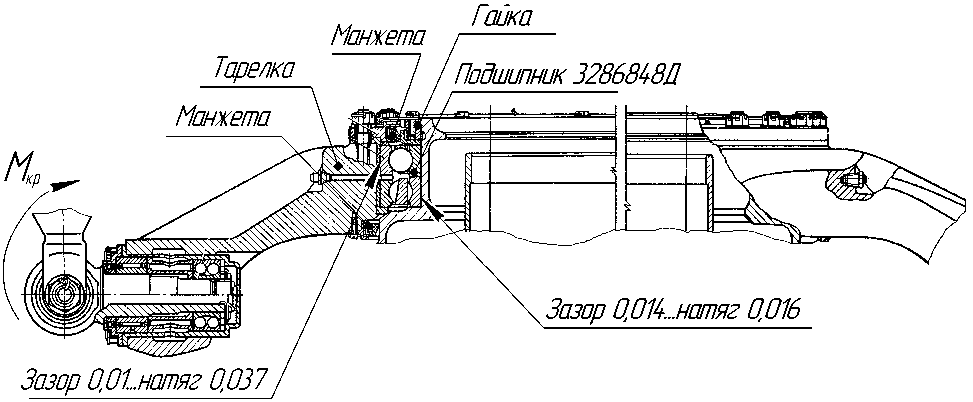
Рис. 1. Схема автомата перекоса несущего винта вертолета

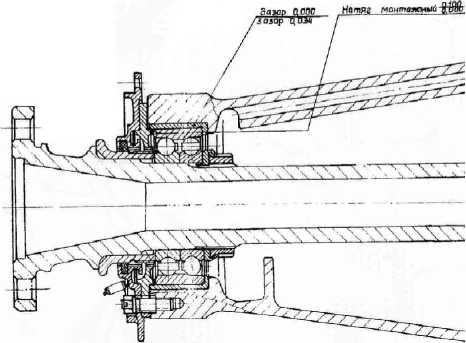
Рис. 2. Схема опоры вала рулевого винта вертолета

В контакте шарика с наружным кольцом имеется качение с верчением.

Момент трения качения для каждого ряда шариков определим по известной зависимости [3]:

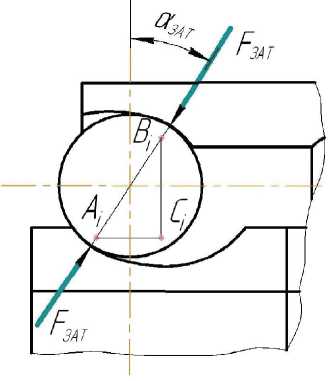
Рис. 4. Силовые и геометрические соотношения при затяжке

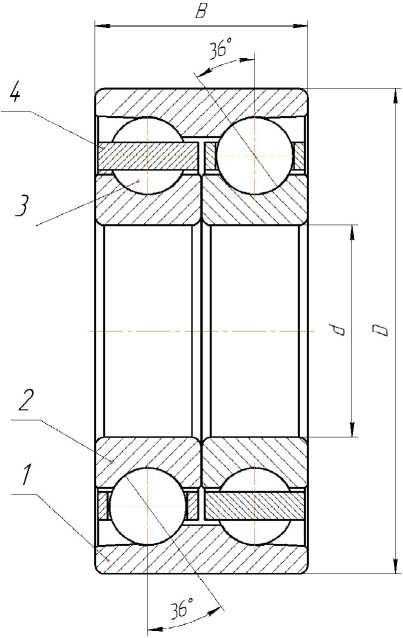
Рис. 3. Общий вид подшипника

М

кач

fк F3am tg^a

зат .

Момент трения верчения на эллиптической

площадке контакта определим по [5]:

T = 3 n • f • F_3am • a_H • S /( 16 ( 1 + m )) . верч             зат н

Здесь f к и f – коэффициенты трения качения и скольжения в контакте [3], a н и b н – размеры полуосей площадки контакта шарика с желобом наружного кольца.

При приближенных вычислениях S - значение сходящегося ряда, вычисляемого по формуле:

2 m²

S = 1 + —. ■

m ⁴ • 1 2

2² ⋅ 4²

m⁶ ⋅ 1² ⋅ 3²

2² • 4² • 6 2 ⁺ ""

Здесь m = ( a - b )/( a + b ) .

нн нн

Пренебрегая при малых скоростях вращения

сопротивлением на перемешивание воздушно-масляной среды и сопротивлением сепаратора, общий момент сопротивления вращению для од- ного ряда шариков можно определить суммиро-

ванием: М сопр    М кач ⁺ Т eep4 •

Момент сопротивления вращению наружно- го кольца при затяжке будет равен

м = м , + м сопр       сопр 1      сопр 2

Если момент сопротивления вращению пре- вышает заданный техническими требованиями, необходимо уменьшить усилие предварительной затяжки.

Значения посадочных натягов колец изменяются вследствие теплового и центробежного расширения деталей подшипникового узла. Расчет деформаций колец от центробежного расшире- ния и посадочных натягов внутреннего кольца выполняется, как показано в [4].

В рабочих условиях в связи с деформациями колец от теплового и центробежного расширения, а также от посадочных натягов рабочие характеристики подшипника, включая радиальные зазоры и углы контакта каждого ряда, и усилие затяжки внутренних колец будут изменяться.

Увеличение диаметров колец и шариков вследствие теплового расширения определится зависимостями, приведенными в [5].

При нагружении подшипника происходят радиальное и осевое перемещения, а также пово- рот внутреннего кольца относительно наружного. Изменения осевого и радиального смещений при перекосе кольца зависят от углового положения ϕ рассматриваемого шарика относительно линии действия радиальной нагрузки.

Силовые и геометрические соотношения для шарика, расположенного под произвольным углом ϕ , показаны на рис. 5 и 6.

При отсутствии контакта с внутренним кольцом принимаем:

F ei = 0 ; F Hi ^_ F c ; ^ h, ^_ ^ с

aei = arctg(Si/(Hi - R + 0,5 Dw - Sc )).

При наличии контакта шарика с внутренним кольцом геометрические и силовые соотношения по рисунку 6 будут иметь вид:

F F       F ei    _     Hi _ c sin aHi   sin aei   sin(aei - aHi ) ;

⁽ R e ^- 0,5D w ⁺ § e ) sin ^a ei ■

( R H - 0,5D w + 5 h ) sin « Hi = S i ;

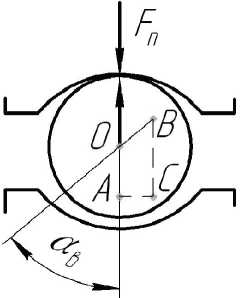
Рис. 5. Силовые и геометрические соотношения для шарика, при отсутствии контакта с внутренним кольцом

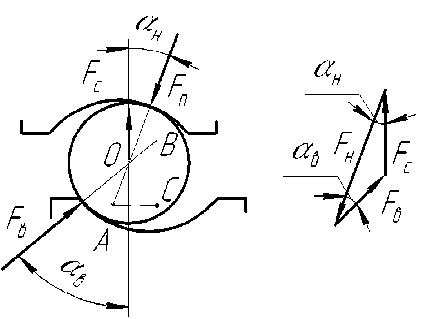
Рис. 6. Силовые и геометрические соотношения для шарика, при наличии контакта с внутренним кольцом

^{( R} e - 0.5^D _w ⁺ S e ) cOs ^a ei ⁺

( R h - 0.5D w + S h ) cos a Hi = H,.

Здесь: F _вi , F_нi – усилия в контактах; F_c – центробежная сила; α _вi , α _нi – углы контакта; δ _в , δ _н – деформации в контактах; S_i , H_i – осевое и радиальное смещения центров желобов колец в рассматриваемом сечении.

Полученная система уравнений решается относительно углов контакта методом Ньютона.

При известных значениях усилий и углов контакта шариков с кольцами нагрузки подшипника определятся из условия равновесия внутреннего кольца:

Fr = lbF1elcOS aieicos ф + i=1

∑z F2вicosα2вicosϕ i=1

и ^F a = ^L^F lei sin ^a1ei - ^L^F2 ei sin ^a2ei ■ i = 1                         i = 1

Усилия в контакте шариков нагруженного ряда с кольцами создают опрокидывающий момент. Действующий на внутреннее кольцо со стороны шарика момент определим по формуле:

M 01 = F 1 Bi • D 0 в (sin ^a 1 Bi )/2 , где D_0в – диаметр по центрам желоба внутреннего кольца.

Усилия в контакте шариков разгруженного ряда с кольцами также создают опрокидывающий момент, действующий на внутреннее кольцо:

M 02 i = F 2 Bi • D 0 в sin ^a 2Bi /2 .

При симметричном расположении шариков условие равновесия кольца под действием момента будет иметь вид:

( A

T F1BisinaiBi - i=1

z

T F 2в., sin ^a 2в..

V i = 1                  7

• D 0 в cos ^ ²

Приведенная система уравнений равновесия и ранее приведенных геометрических соотношений позволяет определить перекос и смещения колец, а также распределение усилий и углов контакта в подшипнике.

Решение системы уравнений выполняется численно комбинированным методом. Во внутреннем цикле при принятом значении перекоса ^ определяются радиальное S r и осевое S a смещения колец из решения методом Ньютона системы двух нелинейных уравнений:

Ф 1 ( S r ,S_a, v ) - F r

z

- T F1Bi cos a1 Bi cos Ф i=1

После определения усилий и углов контакта вычисляются для всех шариков размеры площадок контакта с внутренним и наружным кольцами. Вычисляются расстояния от края площадки контакта до кромки бортика и проверяются условия отсутствия выкатывания шариков на кромки бортиков колец или замка.

Долговечность подшипника определяется по контактной выносливости с учетом вероятности разрушения двух рядов.

После определения усилий и углов контакта шариков с кольцами вычисляются контактные напряжения: О _вц , О нц , О _в 2 i , О н 2 i и размеры полуосей эллипсов контакта a в ₁ i , a в ₂ i , a н ₁ i и a н ₂ i , как показано ранее.

Долговечности каждого из желобов колец находятся по уравнению контактной выносливости [5]:

^N цв1 = ¹⁰ ( ^О в/ ^О Ев1 ) 9 ;

^N цв 2 = ^{10 (<7}бв ^ Е2 2 ) ;

^N цн1 = ¹⁰ ( О бнн ,С^ Ен1 ) 9 ;

^н2 = ¹⁰ 7 ^(о бн °^ГЕ22 ) 9 -

Здесь: О б_в , О бн — базовые контактные напряжения, соответствующие 10 ⁷ циклов перемены контактных напряжений для внутреннего и наружного колец; ^О Ев 1 , ^О Ев 2 , ^О Ен 1 , ^О Ен 2 ^- значения эквивалентных контактных напряжений для соответствующих желобов колец.

Для вращающегося внутреннего кольца эквивалентные напряжения определяются на основе теории линейного суммирования повреждений:

z

— T ^F2 Bi cos ^a 2 Bi cos ф = ⁰

i = 1

1 i = zz

₁ z ₉

^О Ев 1 = 9    ^{T o} xe1i и

^О Ев 2

1 i = ^z

= 99 F T О \ z i =1

9 хв 2 i

и _z

⁺ T ^F2 Bi ^{sin a} 2 Bi = 0.

i = 1

Затем во внешнем цикле методом хорд уточняется значение угла перекоса ^ из решения уравнения:

Ф з ( S„S . ^ ) - M -

z T F1 Bi ^ sin a 1Bi - I=1 z • D0 B cos ф / 2 = 0 T F2i V1=1 sin a2 Bi 7 где О xB 1 i и ОXB 2 i - расчетные напряжения в контакте данного шарика с желобом в плоскости, проходящей через центр площадки контакта максимально нагруженного шарика, как показано в [5].

Для неподвижного наружного кольца эквивалентные напряжения находим по зависимостям:

^О E 21

1z

=10 _T

z v i=1

^О 2 1i ^{и О} E 2 2

z

1T О z i=1

10 н2i .

При суммировании учитываются только напряжения, превышающие предел контактной выносливости:

^О хв 1 i >  ^О H lim, ^О хв 2 i >  ^О H lim, ^О 2 1 i >  ^О H lim ^{и О} н 2 i >  ^О Н lim.

Зная число циклов нагружения до разруше- ния, долговечность соответствующих желобов колец определяем по зависимостям:

N л               N i

' цв 1        l _ цв 2

60 z ( n - n 0 ) ’ h^{B 2}     60 z ( n - n о )’

ΝΝ

ЦН 1 l              ЦН 2

60 z ( n - n 0 ) ; h^{H 2}    60 z ( n - n 0 ) ^.

Здесь: z – число шариков в одном ряду, n и n₀ – частоты вращения внутреннего кольца и сепаратора.

Используя известные соотношения, долговечность подшипника в целом определяется по формуле:

- 1,11       - 1,11       - 1,11       - 1,11 ^{- 0,9}

L h = ^{( L} he 1 + L he 2 + L hn 1 + L hH 2 )     ^.

Для стороны желоба, не имеющей контакта с шариками, соответствующее отношение L ^- _hj ^{1 ,11} принимается равным нулю.

В качестве примера рассмотрим двухрядный шариковый подшипник 286896, установленный в автомате перекоса несущего винта вертолета МИ. Геометрические размеры подшипника определяем по чертежу.

Частота вращения подшипника n = 132 об./ мин., осевая нагрузка F a = 13,35 кН, радиальная нагрузка F r = 5,0 кН. Усилие предварительной затяжки внутренних полуколец определялось в зависимости от начального значения зазора между торцами внутренних полуколец.

На рис. 7 – 9 приведены результаты расчета подшипника.

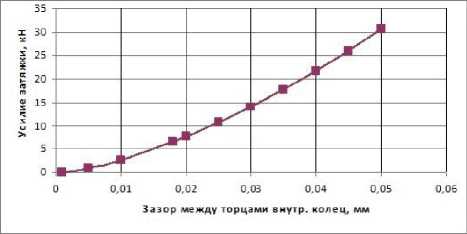
Рис. 7. Зависимость усилия затяжки подшипника 286896 от зазора между внутренними кольцами

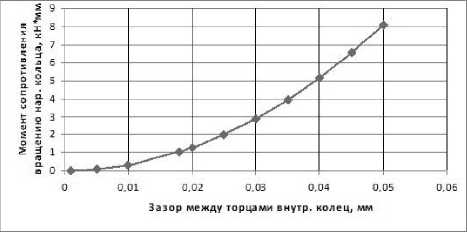
Рис. 8. Зависимость момента сопротивления вращению подшипника 286896 от зазора между внутренними кольцами

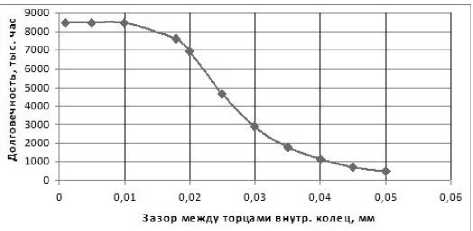
Рис. 9. Зависимость долговечности подшипника 286896 от зазора между внутренними кольцами

Видно, что при зазорах между торцами внутренних колец, превышающих 0,01 мм, наблюдается снижение долговечности подшипника. Таким образом, при сборке подшипника целесообразно обеспечивать зазор между торцами не более 0,01мм. При этом усилие затяжки будет не более 3,5 кН. При контроле усилия затяжки момент сопротивления вращению наружного кольца при стянутых внутренних не должен превышать 350 Н·мм.

Рассмотрим подшипник 3156211, установленный в опоре вала рулевого винта вертолета МИ-8. Основные размеры подшипника по чертежу. Частота вращения подшипника n = 1120 об./ мин., осевая нагрузка F a = 8,24 кН, радиальная нагрузка F r =2,28 кН. Опрокидывающий момент M =24,5 кНЧм.

На рис. 10 и 11 приведены результаты расчета усилий и углов контакта шариков с кольцами. Здесь 1-й ряд шариков – ряд, нагружаемый в рабочих условиях осевой силой тяги винта, 2-й ряд – разгружаемый в рабочих условиях. В то же время оба ряда шариков нагружаются усилием предварительной затяжки и моментной нагрузкой.

Под действием рабочих нагрузок внутреннее кольцо смещается относительно наружного на 28,45 мкм в осевом направлении. Наружное кольцо перекашивается относительно внутреннего на угол 1,7 минуты. Допускаемый угол свободного поворота колец при принятом значении радиального зазора равен 5,49 минуты. При этом происходит радиальное смещение внутреннего кольца на 16,31 мкм в сторону, противоположную направлению радиальной нагрузки.

Приведенные на рис. 10 результаты показывают, что в рабочих условиях часть шариков не воспринимает нагрузку. Необычным является то, что максимальное усилие возникает в контакте шарика 2-го ряда. Так максимальное усилие в контакте шариков 1-го ряда составило 11,727 кН, в контакте шариков 2-го ряда – 12,448 кН. Соответственно максимальные значения контактных напряжений в контактах шариков 1-го ряда со-ставили σ в ₁ =1341,6 МПа и σ н ₁ =1367,9 МПа, в контактах шариков 2-го ряда - σ в ₂ =1351,0 МПа и σ н ₂ =1372,0 МПа. Следовательно, долговечность подшипника по контактному выкра-

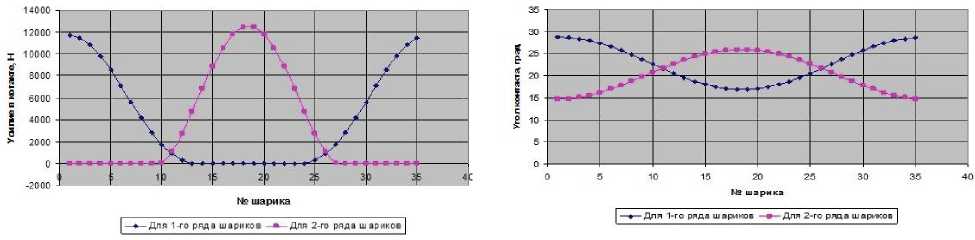
Рис. 11. Распределение углов контакта шариков с кольцами при нагружении

Рис. 10. Распределение усилий в контактах шариков с кольцами при нагружении усилиями и моментом усилиями и моментом.

шиванию поверхностей будет определяться долговечностью 2-го ряда.

При расчетах долговечности подшипника по рекомендациям [5] приняты значения базовых контактных напряжений для подшипниковых сталей равными σ б =2500 МПа, предела контактной выносливости - σ _lim =800 МПа.

Для принятых условий работы расчетная долговечность подшипника составила L h =4990 часов.

Расчёты показали, что увеличение долговечности с ростом усилия преднатяга наблюдается только при малых значениях преднатяга. Но при этих малых усилиях преднатяга происходит разгрузка под действием рабочей осевой нагрузки шариков второго ряда. Таким образом, оптимальным значением усилия преднатяга для данных условий работы подшипника 286896 является 8 – 10 кН.

Результаты расчетов показали, что при заданных заказчиком условиях работы выкатывание шариков на кромку бортика кольца не наблюдается.

Исследования показали также, что опрокидывающий момент существенно изменяет характер распределения усилий в контактах и углов контакта шариков с желобами колец нагруженного и разгруженного рядов. При этом максимальные значения усилий и напряжений в контактах шариков могут наблюдаться в разгруженном ряду.

Показано, что долговечность подшипника зависит от величины усилия предварительной затяжки внутренних колец. При этом при небольшом усилии затяжки возможна полная разгрузка второго ряда шариков при осевом нагружении подшипника. В то же время при усилиях предна-тяга, исключающих разгрузку второго ряда шариков, долговечность подшипника уменьшается с увеличением усилия предварительного натяга.