Расчёт характеристик вихревых систем термостатирования

Однако одной из существенных проблем, ограничивающих использование вихревых устройств, является довольно узкий диапазон высотно-скоростных характеристик летательного аппарата, в пределах которого достигается необходимый уровень термостатирования. Причиной этого является неизменность геометрических параметров вихревых устройств при изменении параметров входного потока. Поэтому разработка систем термостатирования на базе вихревых устройств – вихревых систем термостатирования, позволяющих решить проблему поддержания необходимых климатических условий для эксплуатации бортового оборудования аэрокосмической техники является назревшей актуальной проблемой.

Основным недостатком исследований и практических разработок является то, что они не дают возможности определения функциональных зависимостей между геометрическими размерами вихревой трубы и параметрами выходных потоков газа на выходах из нее. Полуэмпирические зависимости, выведенные для конкретных геометрических соотношений, не являются целесообразными.

При расчете геометрических размеров вихревых труб был использован расчетный аппарат, основанный на уточненной методике Меркулова. Исходными данными для расчета являются: потребные температура T_x холодного потока, холодопроизводительность Q_x и давление p_x холодного потока. Давление p ₁ температура T ₁ и относительная влажность ϕ ₁ набегающего потока задаются и корректируются, исходя из данных о внешней среде.

По условиям отвода тепла от охлаждаемого объекта задается допустимая величина изобарного подогрева Δ T_k холодного потока при теплообмене с охлаждаемым объектом.

По этим величинам и известной величине изобарной теплоемкости C _p газа определяется потребный массовый расход холодного потока:

Gx = С^^Атк •       (1)

где A T_k - допустимая величина изобарного подогрева.

Далее определяется располагаемая степень расширения газа:

жиму, когда давления на оси вихря равно давлению холодного потока. Таким образом, подсчитываем скорость истечения по выражению:

v ₁

к • R • T1

к -1

Г 1 А

к-1 к

P 1 п = —

P x ^.

V п ;

,

и относительная температура холодного потока:

T x

0 x = --

T 1

.

Затем в первом приближении определяются размеры вихревой трубы, для чего по полученным значениям 0 x и п из обобщенных характеристик определяется потребное значение

затем критическую акр2 = kRT1 и безразмерную v1

Л = — скорости. Определение площади проа кр ходного сечения сопла при докритическом истечении удобно проводить по газодинамической функции - приведенному расходу q(l):

д - большее для данного значения п , и подсчитывается потребный общий расход сжатого газа:

q (Л) = Л-

к + 1 Г,

------------------• I 1

2 V

к - 1

к + 1

• Л

^{к - 1} . (9)

G x

G =-

.

д

По значению этой функции легко определяется площадь проходного сечения сопла при док-ритическом истечении:

По общему расходу и параметрам входа определяется площадь проходного сечения сопла. Если располагаемая степень расширения п > 4, то в сопловом сечении имеет место критическое истечение и площадь сопла подсчитывается по выражению:

F c =

F кр

q ( Л ) .

F kp

к + 1

G^R • T 1 Г к + 1 А 2 ( к - 1 ] а • P 1 V 2    )

Здесь F _кр подсчитывается по выражению (6).

При использовании прямоугольных тангенциальных входных сопел рекомендуется принимать их осевую ширину b вдвое большей их высоты h по выражениям:

Здесь а - коэффициент расхода сопла, который согласно исследованиям составляет величину 0,96.

При использовании в качестве рабочего тела воздуха ( к = 1,4, R = 287 Дж / кг • К ) и подстановке р 1 = 10 5 Па , выражение (5) приводится к виду:

h =

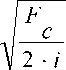
b =

F

c

.

i • h

F kp

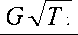
0 , 38 P 1

При располагаемой степени расширения п < 4, скорость истечения из сопла докритичес-кая, определяется по выражению:

к • R • T 1

к - 1

в котором вместо величины п подставляется величина п . Такая замена обоснована тем, что оптимальный режим работы вихревой трубы соответствует нулевой осевой скорости холодного потока на оси вихря соплового сечения, т. е. ре-

Для определения диаметра D вихревой трубы необходимо задаться значением относительной площади сопла F _кр . Она не играет определяющей роли, но может быть оптимизирована из соображений, вытекающих из полученных ранее аналитических зависимостей.

Для авиационных систем термостатирования при умеренных степенях расширения и давления холодного потока, близкого к атмосферному, оптимальным значением относительной площади сопла следует считать F _COTH = 0 . Увеличение F _{с отн} несколько увеличивает эффект охлаждения холодного потока на малых д (снижает эффект подмешивания пограничного слоя), но уменьшает эффект охлаждения при больших д (повышает осевые скорости и уровень давления в вихревой зоне). С ростом F_с уменьшаются габаритные размеры вихревой трубы.

Можно рекомендовать при умеренных давлениях на входе 2 <  p ₁ < 6 ·10⁵ Па, степенях расширения 2 <  п <  6 массовых долях холодного потока 0,2 <  д < 0,8 принимать значения 0,09<

F _{с отн} <0,10. При высоких давлениях 6 <  p ₁ < 12 40 5 Па на входе, степенях расширения п >  6, массовых долях 0,5 <  Ц < 1,0 принимать 0,07< F _{с отн} <0,09. При низком давлении p ₁ <  10⁵ Па на входе (например, высотные условия), умеренных Ц и п принимать 0,1< F _C0TH <0, Близкие к рекомендуемым значениям дает соотношение:

F c

= 0 . 327

1 f 1 ^ к. V п J

По расчетному значению F_с и принятой величине F _{с отн} определяется диаметр вихревой трубы:

D =

4 • F

c

= 1 . 13 •

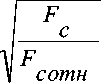
. (13)

3.14 • F cотн

Для более точного расчета необходимо ввести поправки на масштаб вихревой трубы, влажность поступающего сжатого газа и уровень давлений.

В экспериментах была получена зависимость относительной температуры 0 x от диаметра D вихревой трубы. Аналогичную зависимость можно использовать в диапазоне 5 <  D < 50 мм и, принимая за базовые обобщенные характеристики экспериментальные 0 x , построенные для вихревой трубы с D = 24 мм, представить ее в виде:

А = 0 , 005 • (D - 24 ) . (14)

По этой величине находим поправку А0 x по выражению:

А0 x = А^

к - 1 1 ^ к п )

а затем и уточненное значение 0 Х = 0 x + А0 x , по которому из обобщенных характеристик определяем уточненное значение массовой доли Ц .

Далее расчет повторяется в описанном выше порядке. Диаметр отверстия диафрагмы подсчитывается по выражению из:

dд =(0,350 +0,313 m)D. (16)

Длина вихревой зоны L принимается равной 9 диаметрам вихревой трубы:

L=9D . (17)

При таком выборе длины вихревая зона на горячем конце должна быть ограничена спрямляющей крестовиной.

В случае автономной работы вихревой трубы этих величин оказывается достаточно для полного расчета. Если же вихревая труба используется в какой-либо схеме, то часто появляется необходимость определить на выбранном режи- ме давление горячего потока перед дросселем.

Для определения этой зависимости удобно ввести безразмерную величину - степень недо-расширения горячего потока:

Pr

Px ^,

характеризующую энергетический уровень горячего потока по давлению.

Согласно проведенным экспериментам при длине вихревой трубы в 9 калибров и оптимальных для выбранного Ц диаметрах отверстия диафрагмы величина п Г является функцией только п и в диапазоне 2 <  п <  6 может быть связана с последней простым соотношением:

п Г = 0,33 • п + 0,67 . (19)

Таким образом, при заданных параметрах p ₁ и T ₁ сжатого газа и давления p_x холодного потока обобщенные характеристики совместно с выражением (9) позволяют определить все требуемые параметры выходящих из вихревой трубы потоков.

В расчете пользуются зависимостью 0 х = 0 _х ( ц , п ), которая была получена эмпирически. Для автоматизации расчета было необходимо получить эту зависимость в аналитическом виде. Была проведена аппроксимация этой зависимости полиномом 9-ой степени, для выборочных, необходимых значений п . Среднеквадратичная ошибка аппроксимации не превышает 0.0002 или 2%, относительно значения 0 _x . Аналогичная работа произведена с зависимостью § = £ ( p х ).

Для расчета геометрических параметров вихревых труб применяется итеративный метод последовательных приближений, основанный на уточненной методике Меркулова, приведенной выше (рис.1)

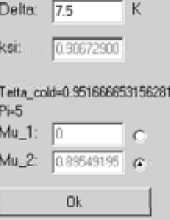
При определенных величинах 0 x и п значение Ц не является однозначным. Однако, из произведенных расчетов видно, что в случаях неоднозначности необходимо брать большее Ц . Иначе данная методика расчета не позволяет получить устоявшееся решение. В соответствии с представленным алгоритмом разработана программа расчета геометрических размеров вихревых труб (рис. 2)

Для проверки предположения, о том, что одну и ту же вихревую трубу можно использовать при других входных параметрах давления и температуры, и при этом получать на выходе необходимую холодную температуру, был разработан алгоритм, рассчитывающий количество “эквивалентных” вихревых труб при условии, что трубы можно считать эквивалентными, когда они мало различаются по размерам (в пределах 5%) и при этом температура холодного потока на выходе трубы отличается не более чем на 10%. Алгоритм заключается в следующем: после расчета интересующей нас трубы, путем перебора T ₁ и p ₁ , полу-

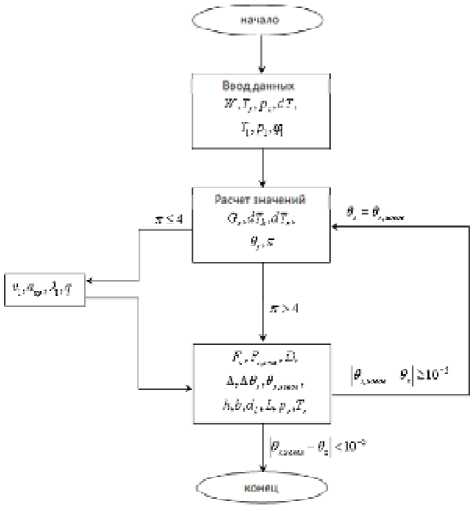
Рис. 1. Алгоритм расчета геометрических параметров вихревой трубы

чаем новое количество труб, далее, их параметры сравниваются с исходными, и, в случае эквивалентности, считаем что интересующая нас труба может использоваться при аналогичных внешних условиях. На рисунке показан случай, при кото-

Fddy Convection

Result

G »00279755043983459 kg/toc FJet ■ 121 04615020752 mm‘2 D- 32.18/0002746582 mm 5- 7 /7965/840/2876 mm b - 15 5593156814575 mm d drop - 20 0352516174316 mm L- 289 683013916016 mm p_hot* 0 497999995946004 bar T_hot= 407 487915039063 К

jCdk-jtae court d txnte tube» j rout of simlv KftM 27

Рис. 3. Рабочий фрагмент программы расчета

Fdtly Convection	-njxJ
w      |2O0      V/
T.cokl: |мз       К	Della |?§        К
p.cold |03       Bar	<5.
dT     |ю       К	I Me cdd.0 9684907664222 72
p1:       |c9        Bor	PM
61:        |05	Mu J: |n         c
T1       1300        К	Mu_2 №D43227 (7
Stet	к
1	1
G - 0 0229755043983459 kg/sec
FJet- 121 04615020752 mm	*2
0 - 32,18/0002/46582 mm
h- 7 //965/840/2876 mm
b- 15 5593156814575 mm
d diap - 20 0352516174316	mm
^- 289 683013916016 mm
pj.ul- 8 497999995946004	ini
T hut- 407 487916039063 К

C*Uaie cent ol smie tube          Coverrg

Рис. 2. Рабочий фрагмент программы расчета ром существуют 27 труб (рис. 3), эквивалентных просчитанной. То есть гипотеза о возможности использовать вихревую трубу с одинаковыми геометрическими параметрами в разных точках диапазона высот и скоростей летательных аппаратов подтверждается.

Чтобы найти количество труб, для покрытия диапазона высот и скоростей полета летательного аппарата, соответствующим возможным входным температурам большого диапазона, например T ₁ от 240 К до 350 К, и входным давлениям p 1 = a-p_x (где п =2,3,4,5,6,7,8,9,10,12), былраз-работан алгоритм, который, фактически, повторяет алгоритм поиска “эквивалентных труб” при всех входных значениях T ₁ и p ₁ .

Дляусловий T_x = 293, W = 200, p_x = 0,3 и различных п было просчитано количество труб покрывающих описанное выше множество. К примеру, для p_x = 0,3 необходимо 39 различных труб. Область покрытия указана в табл. 1 (без учета последовательного использования труб).

Таблица 1. Область покрытия возможных входных температур

ТЕ	296	297	298	299	300	301	302	303	304	305	306	307	308	309	310
2	1	1	1	1	1	1	1	2	2	2	2	3	3	3	4
3				5	5	5	5	5	5	5	5	5	5	5	6
4										10	10	10	10	10	10
5												17	17	17	17
6												24	24	24	24
8										29	29	29	29	29	29
10									35	35	35	35	35	35	35
12								38	38	38	38	38	38	35	35

Px	Tx	311	312	313	314	315	316	317	318	319	320	321	322	323	324	325
2
3		6	6	6	6	6	7	7	7	7	7	7	8	8	8	1
4		10	10	10	11	12	14	15	15	15	15	15	15	15	15	16
5		17	17	17	17	17	18	19	10	10	10	10	10	10	10	10
6		24	24	24	17	17	17	17	17	17	17	17	17	17	17	17
8		29	29	29	29	29	30	32	32	32	32	32	24	24	24	24
10		35	35	35	29	29	29	29	29	29	29	29	29	29	29	29
12		35	35	35	35	35	35	35	35	35	35	35	35	35	35	35

7Г	326	327	328	329	330	331	332	333	334	335	336	337	338	339	340
2
3	8	9	9
4	16	5	5	5	5	5	5	5	5	6	6	6	6	7	7
5	10	10	10	10	10	10	11	13	14	15	15	15	15	15	16
6	17	17	17	17	17	17	19	21	10	10	10	10	10	10	10
8	24	24	24	24	24	24	24	24	24	24	24	24	25	27	28
10	29	29	29	29	29	29	29	30	32	32	32	32	32	32	32
12	35	35	35	39	39	39	39	39	39	29	29	29	29	29	29

7Г	341	342	343	344	345	346	347	348	349	350
2
3
4	7
5	16	16	16	16	16	23	23	23	23	23
6	10	10	10	11	13	15	15	15	15	15
8	33	33	33	33	33	33	33	34	34	34
10	32	37	37	37	37	37	37	33	33	33
12	29	29	29	29	31	32	32	32	32	32

Tube №29

Entry conditions:

W = 200

T_cold = 293 p_cold = 0.3 dTk = 10

T1 = 301

p1 = 4 fi1 = 0.5

Result:

G = 0.0223092

F_jet = 44397 D = 2279 h = 4.6065 b = 9.213 d_diap = 14.6798 L = 209.511 p_hot = 0.993 T_hot = 449.056

0,2 3,3 0,4 0,5 0,6 0,7 0,8 0П 1 1,1 1,2 выходное давление, ат

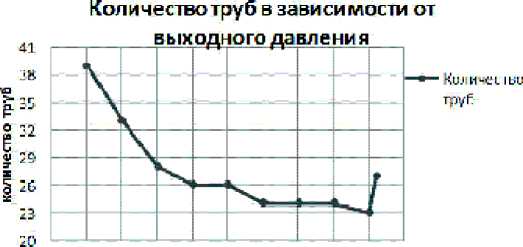
Рис. 4. Расчет количества труб в зависимости от внешних условий

При исследовании зависимости количества труб необходимых для покрытия диапазона высот и скоростей полета и px , выяснилось, что можно указать лучшее px , для которого количество труб будет меньше. Так, при px = 1,1 • 105 Па необходимо лишь 23 трубы с различными геометрическими параметрами. А уже при px = 1,12 • 105 Па необходимо уже 27 труб. Далее их количество только возрастает. Таким образом, для упомянутых входных данных, наиболее оп- тимальным выходным давлением холодного потока будет являться px = 1.1 • 105 Па , и при этом минимальное количество необходимых труб будет равным 23, (без применения последовательного использования) см. рис.4 .

При недостаточном охлаждении потока, можно последовательно пропускать поток через 2, 3 и т.д. труб. Алгоритм расчета выходных параметров из последней вихревой трубы (Рис. 5) заключается в следующем: входные параметры

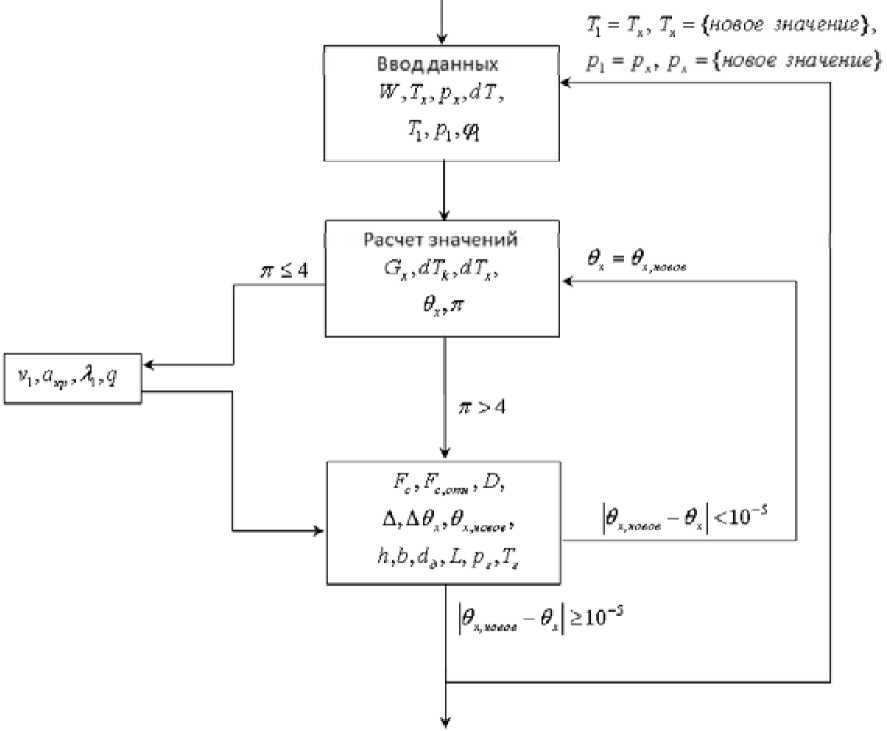
Рис. 5. Алгоритм расчета выходных параметров из последней вихревой трубы в составе ступенчатого подключения

второй трубы T ₁ и p ₁ , являются выходными T_x и p_x для первой с учетом допущения, что из-за малой длины соединительных каналов между вихревыми трубами поток не успевает нагреваться и не теряет уровень давлений.

С помощью уточненной методики Меркулова расчета геометрических параметров вихревой трубы была разработана программа для определения наименьшего количества вихревых труб, необходимых для кондиционирования бортовых отсеков летательных аппаратов при различных высотно-скоростных характеристиках.