Расчёт и анализ трёхволнового дифракционного фокусирующего дублета

Достоинства и недостатки, сопровождающие применение ДОЭ, хорошо известны [1]. Основной проблемой, возникающей при использовании ДОЭ в полихроматическом излучении, является их высокий хроматизм, делающий практически невозможным использование одиночной дифракционной линзы в изображающих системах [2, 3], хотя для других применений [4, 5] это может и не быть препятствием. Наибольшее внимание исследователей привлекали гибридные дифракционно-рефракционные оптические системы [6, 7], обеспечивающие эффективную коррекцию хроматических аберраций. Однако с точки зрения использования главного преимущества дифракционной оптики – её малого веса, такие системы представляли собой определённый компромисс, так как включали силовые рефракционные элементы весьма больших габаритов и, следовательно, веса. Создание же чисто дифракционных изображающих систем наталкивается на определённые трудности, поскольку очевидно, что невозможно корректировать хроматизм путём комбинации собирающих дифракционных линз, распределяя оптическую силу на несколько элементов.

Известен подход к коррекции хроматизма путём комбинирования двух чисто дифракционных элементов: рассеивающего и собирающего – с разными оптическими силами [8, 9]. Ахроматизация дифракционного дублета достигается за счет дифракционных оптических элементов с модифицированным законом изменения пространственной частоты. В работах [10– 13] ахроматизация достигается за счет использования дифракционных линз с разными оптическими силами, что приводит к увеличению оптических сил входящих в него линз по сравнению с эквивалентной одиночной линзой и порождает дополнительные технологические проблемы. К тому же такой метод позволяет проводить ахроматизацию для достаточно узкого спектрального интервала. Например, космический телескоп [14], рассчитанный по такой методике, имеет полосу частот всего 20 нм (522–542 нм). Наиболее перспективным выглядит применение ДОЭ при работе с линейчатыми спектрами, когда в спектре имеется несколько узких линий, причём не очень близко расположенных. Такими спектрами обладают, например, двух- или трёхволновые светодиоды или переключаемые по длине волны полупроводниковые лазеры. Именно решению такой задачи и посвящена данная статья.

1.    Хроматическая аберрация дифракционных линз

Хроматическая аберрация дифракционной линзы физически объясняется зависимостью угла отклонения света дифракционной решёткой от длины волны. В отличие от дифракционной линзы причиной хроматической аберрации рефракционной линзы является зависимость показателя преломления от длины волны. Данный факт объясняет принципиальное отличие методов коррекции хроматических аберраций для дифракционных и рефракционных линз. Для рефракционных линз существует широкая номенклатура марок оптического стекла с разными показателями преломления и коэффициентами дисперсии. Расчёт ахроматизированных объективов из рефракционных компонент [15] основан на использовании для разных линз разных марок стекла. Показано, что рефракционный дублет (состоящий из двух линз) обеспечивает ахроматиза-цию для двух длин волн. К сожалению, подобных способов управления хроматической аберрацией для дифракционных линз не существует. Хроматическая аберрация дифракционной линзы [1] зависит от высоты рельефа (сколько целых длин волн составляет оптическая длина пути), но технологические ограничения на сегодняшний день таковы, что создать сколько-нибудь светосильную линзу с высоким рельефом не представляется возможным. Поэтому мы сосредоточимся на рассмотрении способов ахроматизации дифракционных оптических систем с высотой рельефа, создающего разность хода в одну длину волны. Конкретная форма профиля будет уточняться позже на основе результатов моделирования.

Рассмотрим освещение бинарной дифракционной линзы радиусом 2 мм с фокусным расстоянием f = 100 мм точечным источником света, расположенным от линзы на расстоянии 50000 мм на оптической оси. На рис. 1 показаны результаты численного моделирования распределения интенсивности на оптической оси для света разных длин волн ( λ 0 = 0,55 мкм,

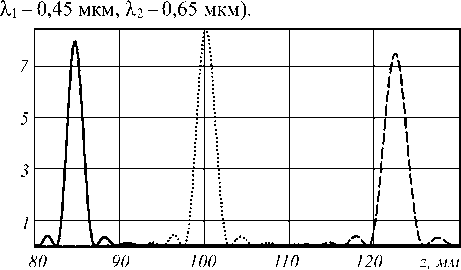
Рис. 1. Фокусировка с помощью бинарной линзы при длинах волн излучения λ 0 = 0,55 мкм (точечная линия), λ 1 = 0,45 мкм (пунктирная линия), λ 2 = 0,65 мкм (сплошная линия)

На рисунке хорошо видно, что разные длины волн фокусируются на расстояниях от линзы, обратно пропорциональных длинам волн, что давно хорошо известно (например, [1]). В результате ни в одной плоскости резкого полихроматического изображения точки не будет. Данный факт усугубляется ещё и тем, что данная высота рельефа (выбранная, например, для длины волны 555 нм) для других длин волн не является оптимальной, что хорошо видно на рис. 1.

2. Основные принципы расчёта трехволнового фокусирующего дифракционного дублета

Основная идея, заложенная при расчёте ахроматического дифракционного дублета (состоящего из двух дифракционных линз), состоит в раздельной фокусировке разных длин волн. Очевидно, что для этого необходимо пространственное разделение по длинам волн. Разделяющим элементом может быть дифракционная решётка, причём для центрированных оптических систем эта решётка должна быть круговой. Такой элемент хорошо известен – это дифракционный аксикон с периодом d . Аксикон в данном случае играет роль диспергирующего элемента.

Схема расчёта дифракционного дублета [6], основанного на диспергирующем действии аксикона, с указанием хода лучей двух разных длин волн приве-

попадают в различные зоны элемента 2. Рассмотрим, каким образом можно сфокусировать падающее на дифракционный оптический элемент 2 излучение, разделённое по различным кольцам для разных длин, в общий фокус на оптической оси. Нужно рассчитать элемент 2 с периодом D , меняющимся по радиусу так, чтобы на оптической оси формировался фокус. Таким образом, элемент 2 выполняет функцию линзы, то есть фокусировки в точку, но в отличие от обычной дифракционной линзы в его фазовой функции должны учитываться меняющиеся по радиусу длины волны падающего излучения. Хроматические свойства некоторых асферических линз были также рассмотрены в работе [16].

На элемент 2 лучи падают под углом α , который определяется из угла дифракции на аксиконе sin α = m λ / d , где m – номер порядка дифракции на ак-сиконе. Угол β между оптической осью и лучом, выходящим из точки элемента 2 на высоте r , определяется из рис. 2:

tg β= r / f ,                                         (1)

где f – фокусное расстояние.

В таком случае направления на максимумы амплитуды после прохождения элемента 2 получаются из равенства:

D (sin β - sin α ) = M λ ,                          (2)

где M – номер порядка дифракции на элементе 2. Так как надо отклонить луч в другую сторону по сравнению с первым элементом, надо считать M отрицательным. Далее везде в формулах M положительно, но знак минус поставлен перед M .

Из (2) имеем sinβ =sinα–Mλ/D; подставив sinα = mλ/d, получим sin в = Х Im - Ml.                             (3)

( d D )

Так как угол предполагается отрицательным, то должно выполняться неравенство

M >  m ( D / d ) .                                 (4)

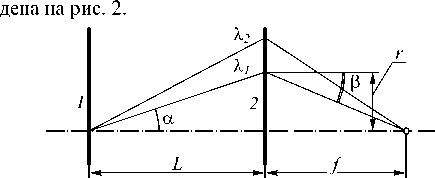
Рис. 2. Схема расчета дифракционного дублета, включающего аксикон

Предположим, что это неравенство выполнено, тогда сменим отсчёт поворота и сделаем угол положительным: sin β = λ ( M / D–m/d ). Выражая тангенс через синус, после приравнивания к величине (1) получим выражение для мгновенного периода:

D ( r ) = M λ ^{d r 2 +} ₂ ^{f 2}₂ . (5) dr + m λ r ² + f ²

Зная период, находим фазовую функцию элемента:

ψ ( r ) =-

2π

r ²

⋅

x« (7^2772

m λ r +

d

.

В зависимости от длины волны лучи, падающие на аксикон 1, дифрагируют под разными углами α и

Единственное направление, в котором просматривается использование такой системы, – это работа с линейчатыми спектрами, когда в спектре имеется несколько узких линий, причём не очень близко распо-

ложенных. Необходимый спектральный интервал между линиями зависит от диаметра входного зрачка системы. Простой расчёт показывает, что для длин волн, показанных на рис. 1, радиус входного зрачка может быть не более 2 мм. В этом случае можно создать сегментированный элемент 2, внутри каждого сегмента которого фазовая функция будет описываться выражением (6) для своей длины волны. При этом сегменты не будут перекрываться.

3. Численное моделирование работы дифракционного дублета

Моделирование работы дифракционного дублета проводилось для указанных выше параметров. Картины дифракции, приведённые на рис. 3, дают представление о структуре пучков разных длин волн в плоскости на расстоянии 100 мм от плоскости аксикона.

На рис. 3 показаны результаты действия дифракционных аксиконов диаметром 4 мм для света разных длин волн ( λ 0 = 0,55 мкм, λ 1 = 0,45 мкм, λ 2 =0,65 мкм).

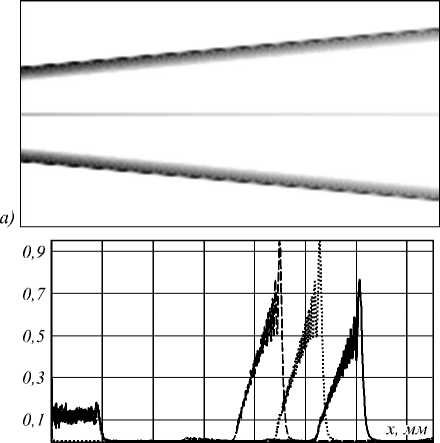
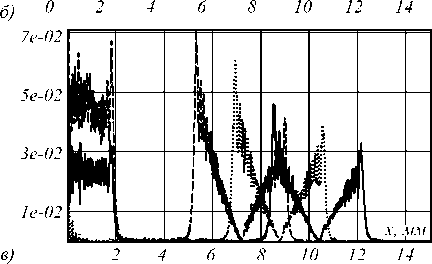
Рис. 3. Действие дифракционного аксикона: распределение на расстоянии z=100 мм от аксикона для многоуровневого рассеивающего аксикона (б) и бинарного аксикона (в) (типы линий в соответствии с рис. 1)

На рис. 3а показан ход расходящихся лучей для базовой длины волны λ0 в сагиттальной плоскости (размер по вертикали – 30 мм, размер по горизонтали – от 50 мм до 110 мм от плоскости аксикона). На рис. 3б показано распределение интенсивности в плоскости, перпенди- кулярной оптической оси на расстоянии 100 мм от ак-сикона для рассеивающего аксикона с профилем зоны, близким к непрерывному, на рис. 3в – то же для бинарного аксикона (видны расходящаяся и сходящаяся волны). Видно, что из-за различия углов дифракции на рис. 3б произошло почти полное пространственное разделение пучков разных длин волн. Незначительное перекрытие максимального радиуса пучка одной длины волны с минимальным радиусом другой не может оказывать сильного влияния, на рис. 3 хорошо видно, что интенсивность для минимальных радиусов невелика вследствии малой площади соответствующих центральных колец на аксиконе.

На рис. 3 б , в вокруг оптической оси хорошо виден нулевой порядок, причём для бинарного аксикона его интенсивность существенно зависит от длины волны (выше уже обращалось внимание на это явление). Моделирование (см. рис. 3 в ) показывает, что у бинарного аксикона даже для указанных длин волн, расстояние между которыми 100 нм, происходит перекрытие порядков (красного и синего цветов), и использовать такой аксикон невозможно. Перекрытие порядков можно устранить, если закрыть центральную зону аксикона диафрагмой, радиус которой определяется углами дифракции максимальной и минимальной длин волн. Но и в этом случае можно использовать только один порядок. Из геометрических соображений ясно, что наиболее компактная система получается, если использовать расходящийся волновой фронт после аксикона. Учитывая пространственное разделение по длинам волн кольцевых распределений, падающих на элемент 2 (см. рис. 3 б ), можно сделать сегментированный фокусирующий элемент (рис. 4), каждый сегмент которого будет иметь фазовую функцию (6) и высоту рельефа, рассчи-

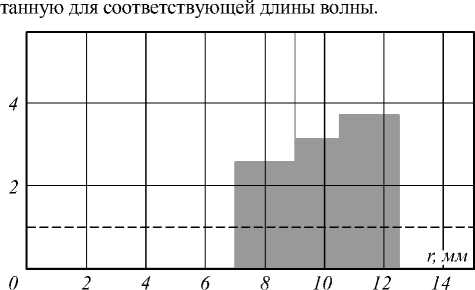
Рис. 4. Высота рельефа сегментированного элемента

Здесь важно отметить, что «платой» за устранение хроматизма будет зависимость числовой апертуры дублета от длины волны. Действительно, легко видеть, что распределение длин волн по радиальной координате приводит к тому, что для больших длин волн (которые дальше от оптической оси) числовая апертура будет больше. Как видно из результатов моделирования (рис. 5), продольная хроматическая аберрация не превышает 0,2 мм для выбранных параметров, а энергетическая эффективность различается не более чем на 20 %.

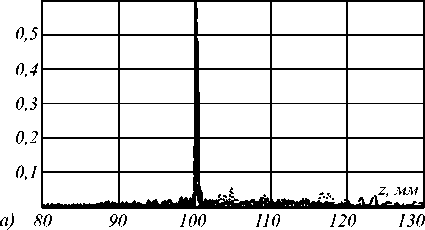
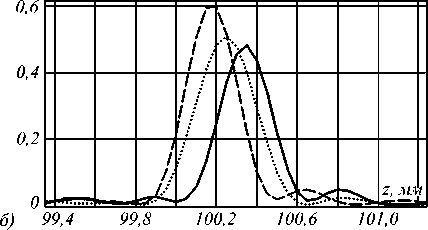
Рис. 5. Действие тандема из аксикона и 3-сегментного ахроаксикона с соответствующей частотой и высотой в каждом сегменте

Результат достаточно хороший, но он получен, к сожалению, для случая линейчатого спектра, который на практике, как уже указывалось, встречается достаточно редко. Из рис. 3 б видно, что при уменьшении расстояния между спектральными линиями (что соответствует переходу к непрерывному спектру или с математической точки зрения переходу от ряда Фурье к интегралу Фурье) будет наблюдаться перекрытие спектральных зон в излучении, попадающем на «ахро-аксикон», и, соответственно, станет невозможным точное сегментирование. Для компенсации этого явления можно лишь уменьшать размер входного зрачка.

Заключение

Проведён расчёт и исследование чисто дифракционного дублета с точки зрения коррекции хроматической аберрации. Показана возможность создания светосильного дублета для линейчатого спектра входного излучения. Предложено решение в виде зонированного элемента для линейчатого спектра. Разработана методика определения параметров компонент для реализации зонированного элемента. Проведено численное моделирование работы зонированного элемента, и показано полное устранение хроматизма для осевого пучка.

Работа выполнена при поддержке Российского научного фонда (грант №14-31-00014).