Расчёт и использование модифицированных относительных фазовых проницаемостей при преобразовании геологической модели в гидродинамическую

Введение. В настоящее время при моделировании разработки нефтяных месторождений широко применяются трёхмерные численные гидродинамические модели многофазной фильтрации. Гидродинамические модели создаются на основе геологических моделей нефтяных месторождений, которые в некоторых случаях могут содержать настолько большое количество ячеек разностной сетки, что время расчётов становится неприемлемым. Поэтому необходимо уменьшить количество ячеек путём объединения мелких ячеек геологической сетки в крупные ячейки гидродинамической сетки. Эквивалентные фильтрационно-ёмкостные параметры крупных ячеек, которые зависят от параметров составляющих их мелких ячеек, естественно определить таким образом, чтобы различие результатов расчётов на исходной и укрупненной сетках было минимальным. Такая процедура в зарубежной литературе называется up’scaling (ремасштабирование) геологической модели в гидродинамическую. В последнее время теория up’scaling’a интенсивно развивается за рубежом (см., например, [1, 2]). Число отечественных публикаций по этой теме значительно меньше. Как отмечается в [1, 3], завершенная теория up’scaling’a в настоящее время ещё не построена.

Эквивалентными параметрами укрупненных ячеек, необходимыми для гидродинамических расчётов, являются пористость горной породы, насыщенности фаз и абсолютная проницаемость пористой среды. Вопросы определения эквивалентных или модифицированных относительных фазовых проницаемостей при up’scaling’е рассматривались в работах [4--7] и обзорах [8, 9].

В настоящей работе предлагается методика определения эквивалентных относительных фазовых проницаемостей (ОФП) при укрупнении ячеек. Методика основана на решении задачи двухфазной фильтрации в отдельной крупной ячейке. Такой способ определения фильтрационных параметров крупных ячеек является наиболее точным среди других методов. Расчётным путём показывается, что если не производить модификацию ОФП, то это может привести к завышенным значениям важнейшего показателя разработки месторождений — коэффициента извлечения нефти (КИН).

Постановка и решение задачи. Рассмотрим процедуру up’scaling’a при следующих допущениях: нефть, вода и пористая среда несжимаемы; вязкости фильтрующихся фаз постоянны; капиллярные и гравитационные силы пренебрежимо малы. Во избежание громоздкости изложения рассматривается случай двумерных ячеек. Расчёт эквивалентных величин осуществим на примере одной из ячеек гидродинамической сетки, так как в остальных их можно определить по аналогии. На рис. 1 в декартовых координатах x1 и x2 приведено схематическое представление процедуры up’scaling’a для крупной ячейки, включающей в себя 8 х 8 = 64 мел- кие ячейки. Через Lk обозначены длины крупной

Вычисление эквивалентных значений скалярных величин, характеризующих ёмкостные свойства крупной ячейки, таких, как пористость породы ϕ и насыщенности фаз S l не вызывает трудностей и определяется путём осреднения по её объёму V [1]:

ϕ ^∗

_V ¹ ϕdV, ϕ ^∗ S l ^∗ = _V ¹ S l ϕdV, V V

V = p v   ( l = w,o ) ,

V

где индексом l внизу отмечены параметры, относящиеся к водной ( l = w ) и нефтяной ( l = o ) фазам. Эквивалентные параметры крупной ячейки отмечены знаком * вверху. Сложнее обстоит дело с определением фильтрационных параметров крупных ячеек, таких, как абсолютная проницаемость пористой среды и относительные проницаемости фаз. Фильтрационные параметры могут быть скалярами, векторами или тензорами.

При вычислении эквивалентной абсолютной проницаемости крупной ячейки в каждой её точке полагается справедливым закон Дарси:

u =

- - Vp,

или в компонентном виде:

( u И ₌ M k 1

I u 2 ) Д ⁰

k 2

( Vp ) 1 A

( Vp )2 ) ■

Здесь kk = kk(x 1 ,x2), uk и (Vp)k d^ - k-я (k = 1, 2) составляющая соответственно диа- гонального тензора абсолютной проницаемости k = ( 0

k 2

, вектора скорости жидкости u и градиента давления Vp; m — вязкость жидкости.

Подставляя выражение (2) в уравнение сохране-

ния массы жидкости div u = 0, можно получить следующее уравнение для давления p(x 1 ,x2) фильтрующейся жидкости, которое решается численно внутри крупной ячейки:

div ^ —Vp^ = 0 ■

Тензор эквивалентной абсолютной проницаемости k ^∗ для крупной ячейки гидродинамической сетки представляет собой коэффициент пропорциональности между средними по объёму скоростью жидкости (u) и градиентом давления (Vp) :

^{( u )} =

V I udV, V

(Vp) = -Ц( Vp ) dV-

V

Тензор k ^∗ определяется из выражения

(u) = - 1 k * (Vp) , или ^μ

( (u) 1 ₌ 1 f k * 1 k * 2       (Vp) 1

I (u) 2 У Д k * 1 k * 2      (Vp) 2 ) ■ ^W

Здесь и далее скобками (•) обозначены вспомогательные средние величины, являющиеся результатом up’scaling’a, но не используемые в расчётах на крупной сетке. Знаком * отмечены величины, необходимые для расчётов на этой сетке.

Для решения дифференциального уравнения (3) необходимо задать условия для давления на границах укрупненной ячейки. Лучше всего их можно было бы взять из решения на мелкой сетке. Однако для этого потребовалось бы решить исходную задачу на геологической сетке, которую и требуется упростить. Поэтому на практике используются следующие наиболее распространенные типы граничных условий [1]:

• а)    — «открытые границы»

• 1.   p (0 ,x 2)     =     1,   p (L1 ,x 2)     =О,

• 2.   p (x 1, 0)     =     1,   p (x 1 ,L 2)     =0,

p ( x 1 , 0) = p ( x 1 ,L 2 ) = 1 - x 1 /L 1 ,

p (0 ,x 2 ) = p ( L 1 ,x 2 ) = 1 - x 2 /L 2 .

• б)    — «закрытые границы»

• 1.   p (0 ,x 2)     =     1,   p (L1 ,x 2)     =0,

• 2.   p (x 1, 0)     =     1,   p (x 1 ,L 2)     =0,

dX 2 ( x 1 , 0) = dX 2 ( x 1 L 2 ) = 0,

dP (0 ,x 2 ) = dP ( L 1 ,x 2 ) = 0.

Здесь каждому типу граничных условий (а или б) соответствуют два варианта их задания (1 и2).

Чтобы определить компоненты тензора k , необходимо сперва выбрать тип граничного условия: а) или б). Затем c выбранным типом граничных условий дважды решить уравнение (3), поочередно рассматривая варианты j = 1 и j = 2. Поскольку векторы (u) и (Vp) имеют две компоненты и уравнение (3) решается для двух различных вариантов граничных условий (j = 1, 2), то для выбранного типа граничных условий становится возможным определение всех четырёх компонент тензора l * _ f k11 k*2 А k I k* 1 k*2 ) -

Система уравнений для определения компонент k имеет вид

(u) 1 = - ¹( k * 1 (Vp) 1 + k 2 ( (Vp) 2 ) , ^μ

(u) 2 = - ¹( k * 1 (Vp) 1 + k * 2 (Vp) 2 ) ,       (6)

μ

(u) 2 = - ¹( k * 1 (Vp) 1 + k * 2 (Vp) 2 ) , ^μ

(u) 2 = -1( k * 1 (Vp) 1 + k * 2 (Vp) 2), μ или с учётом второго из соотношений (4):

k * 1 (Vp) 1 + k 2( (Vp) 2 = (k 11 Vp) 1 + (k 12 Vp) 2, k * 1 (Vp) 1 + k *2 (Vp) 2 = (k 21 Vp) 1 + (k 22 Vp) 2, k * 1 (Vp) 1 + k 22 (Vp) 2 = (k 11 Vp) 1 + (k 12 Vp) 2, k * 1 (Vp) 1 + k *2 (Vp) 2 = (k 21 Vp) 1 + (k 22 Vp) 2 ■

Здесь индексами 1 и 2 вверху отмечены значения для граничных условий с номерами 1 и 2. Индексами 1 и 2 внизу обозначены соответствующие компоненты векторов (u) и (Vp) .

Определенный из системы (6) на основе граничных условий (5) тензор k ^∗ может оказаться несимметричным. Чтобы получить симметричный тензор согласно [1], необходимо решить систему (6) и рассчитать ^{( k 12 +} ₂ ^{k 21 )} . Затем компоненты k ₁ ^∗ ₂ и k ₂ ^∗ ₁ тензора k ^∗ из (6) необходимо заменить на ^{( k 12 +} ₂ ^{k 21 )} , то есть

где S _wb ( t ) — зависимость водонасыщенности на границе от времени, которая должна выбираться из физических соображений или из приближённых решений. Кроме того, внутри крупной ячейки должны быть заданы начальные условия:

S w ( X 1 ,X 2 , 0) = S w o ( X 1 ,X 2 ) . (9)

k 1*2 ^

^{( k} 1 2 + ^k 2 1 )

2         ,

*      ^{( k} 1 2 ^{+ k} 21 )

21 ^ о .    ⁽⁷⁾

В соответствии с (7) тензор k ^∗ уже будет симметричным.

Отметим, что полный тензор k ^∗ может быть определён только при граничных условиях типа а) — «открытые границы». При граничных условиях типа б) — «закрытые границы» — можно вычислить только диагональную часть этого тензора. Действительно, при граничных условиях б) имеем (u) 2 = (u) ² = 0. Поэтому из (6) следует, что

(u) 1 = - ¹ k 1 1 (Vp) 1 = - ¹ (k Y p) 1 , μμ

(u) 2 = -1 k *2 (Vp) 2 = -1 (kYp) 2, μμ и компоненты тензора абсолютной проницаемости для крупной ячейки можно определить с использованием следующих простых формул:

Далее в крупной ячейке рассчитываются средние скорости каждой из фаз:

⁽ u i ^{) j} = V 1 u j dV,

V

(Vp) j = V ¹ J< Vp ) j dV

V

⁽ l = w, o ; j = ¹ , ²⁾ .

Компоненты симметричного тензора модифи цированных ОФП l-й фазы (l = w, o):

^k r l 11    ^k r l 12

rl = krl21   krl22

k 11

^{( k Y} p) 1

(Vp) 1 ’

^k 22 =

^{( k Y} p ^{) 2}

(Vp) 2 ’

l* — P* — n k 12 = k 21 = 0.

Рассмотрим теперь процедуру определения тензоров модифицированных ОФП для водной ( k _{r w} )и нефтяной ( k _{r o} ) фаз с вязкостями μ _w и μ _o . Внутри крупной ячейки скорости фаз определяются на основе обобщённого закона Дарси:

u l = —k ^k rl ⁽ Sw ) Vp    ( i = wo ) ,

μ l

определяются из следующей системы уравнений:

^{( u} l ⁾ 1 =      ^{( k} r1 11 ^k 1 1 ^{(V p )} 1 ^{+ k} rl 12 ^k 1 2 ^{(V p )} 2 ) ,

μ l

(u i ) 2 = - -( k*_rt 21 k 1 1 (Vp) 1 + k ri 22 k 22 (Vp) 2 ) , (10) μ l

^{( u} l ^{) 2} =      ^{( k} r1 11 ^k 1 1 ^{(V p )} 1 ^{+ k} rl 12 ^k 1 2 ^{(V p ) 2 )} ,

μ l

^{( u} l ^{) 2} =      ^{( k} r1 21 ^k 21 ^{(V p )} 1 ^{+ k} rl 22 ^k 22 ^{(V p ) 2 ) .}

μ l

Здесь компоненты тензора k _{r l} рассчитываются аналогично (6)-- (7). Уравнения (10) получены в результате осреднения скоростей фаз, определённых из обобщённого закона Дарси, по объёму крупной ячейки.

Полный тензор модифицированных ОФП, как и полный тензор абсолютной проницаемости, может быть определён только для граничных условий типа а). Для граничных условий типа б) значения диагональных компонент усреднённых ОФП определяются согласно следующим формулам:

и решается следующая система уравнений двухфазной фильтрации [10]:

k rl 11

div

(k (— + —A Vp) μw   μo

= 0 ,

V = div (k — Vp) , Sw + S _o = 1 . (8) ∂t μ w

Система уравнений (8) кроме граничных условий для давления (5) дополняется граничными условиями для насыщенности одной из фаз (для воды). Эти условия задаются на границах, через которые происходит втекание жидкости в ячейку. Для вариантов 1 и 2 имеем

S w (0 ,x 2 ,t ) = S wb ( t ) ,

S w ( x 2 , 0 ,t ) = S wb ( t ) ,

₌ (^k ri ^k Y ^p) 1       , *   ₌ ⁽k ri ^{k Y} p ⁾ 2

k 1 1 (Vp) 1 , ^{rl 22} k * 2 (Vp) 2 , k i 12 = k 1i 21 = 0     ( l = w,o ) ,       (11)

где значения k _{1 1} и k _{2 2} определяются из (5) при условии (7).

Определение зависимости модифицированных ОФП от водонасыщенности осуществляется следующим образом. Внутри крупной ячейки при заданных начальных (9) и граничных (5) условиях на основе системы уравнений (8) решается задача нестационарной двухфазной фильтрации. При этом в каждой точке крупной ячейки и в каждый момент времени рассчитываются насыщенности фаз и давление смеси. Далее согласно (1) вычисляются средние насыщенности фаз по объёму крупной ячейки S ^ = S ^ ( t ), средние значения скоростей и градиентов давления, и согласно (10) или (11) — модифицированные ОФП k ^i = k ri ( t ). При

каждом t значения S _l ^∗ и k _r ^∗ _l ставятся в соответствие друг другу. В результате получаем искомые зависимости:

k ri = k ri ( S W ) ( l = w, o ) ■

Предложенную выше методику можно легко обобщить на трёхмерный случай. В этом случае для определения тензоров k ^∗ и k _r ^∗ _l необходимо решить три задачи с тремя компонентами скоростей фаз и градиентов давления и с тремя вариантами граничных условий. Всего, таким образом, можно определить девять компонент тензоров абсолютной и относительных фазовых проницаемо-стей трёхмерной крупной ячейки. Методика может быть обобщена также на случай, когда в состав крупных ячеек входят мелкие ячейки, вскрытые скважинами.

Обсуждение полученных результатов. Рассмотрим некоторые следствия из полученных выше решений для модифицированных ОФП. Эквивалентная абсолютная и относительные фазовые проницаемости могут быть тензорами, даже если для мелких ячеек они являются скалярами. Это свойство ОФП есть следствие неоднородности параметров мелких ячеек. Тензор модифицированных ОФП не является функцией только параметров мелких ячеек, а зависит от параметров жидкостей (например, отношения вязкостей фаз), времени и от конкретных условий рассматриваемой задачи, то есть начальных и граничных условий. Модифицированные ОФП также зависят от количества мелких ячеек, включенных в крупные ячейки, то есть от степени укрупнения ячеек. Поэтому универсального метода up’scaling’a (когда эквивалентные параметры крупных ячеек зависели бы только от параметров мелких ячеек) как для абсолютной проницаемости, так и для относительных проницаемостей не существует. Поскольку эквивалентные параметры крупных ячеек зависят от решения на мелкой сетке, то для получения приемлемого результата необходимо делать предположение об этом решении или использовать приближённые решения.

Обратимся к результатам расчётов эквивалентных ОФП в некоторых распространенных ситуациях. В качестве примера рассмотрим два случая: 1 — вытеснение нефти водой и 2 — вытеснение нефти нефтью. Первый случай имеет место вблизи скважин, а второй — в чисто нефтяной зоне. Во избежание громоздкости выкладок и для наглядности представления результатов исследование проводилось для двумерной расчётной области в координатах x1 и x2 . Для мелких ячеек ОФП задавались согласно модели «разноцветных жидкостей», когда krl линейно зависят от Srl, а вязкости фаз одинаковы. Численное решение задачи двухфазной фильтрации (то есть уравнения для водонасыщенности) проводилось методом линий тока [11], обладающим высокой точностью, а также возможностью наглядного представления фильтрационных потоков.

Для давления задавались граничные условия типа а), при которых тензор модифицированных ОФП является диагональным. Для водонасыщен-ности задавались следующие варианты граничных и начальных условий:

S wb ⁽ t )    S W, max , ^S w 0 ⁽ x 1 ^,x 2 )    ^S w, min ,

S wb ⁽ t )    ^S _w min , S w 0 ⁽ x 1 ^,x 2 )    S w, min ■

Для исходных ОФП S _w, _min = S _wc и S w, max = 1 - S or , где S wc и S or — значения критических насыщенностей, при которых соответствующая фаза теряет подвижность. При граничных условиях (12) средняя водонасыщенность в крупной ячейке S _w ^∗ с течением времени может изменяться во всем подвижном диапазоне от S _wc до 1 — S or . В расчётах вязкости фаз полагались равными 1 спз; значения критических насыщенностей S _wc и S _or для мелких ячеек-коллекторов — 0 , 2; проницаемость изотропной пористой среды — 100 мД, пористость — 0 , 2. Для ячеек-неколлекто-ров эти параметры равны нулю. Во всех ячейках-коллекторах задавался одинаковый вид ОФП.

Поскольку начальные условия для случаев (12) и (13) совпадают, то при t = 0 совпадают и ОФП. Таким образом, ОФП для случая (13) можно определить в процессе определения для случая (12). Поэтому в дальнейшем рассматривается только случай (12).

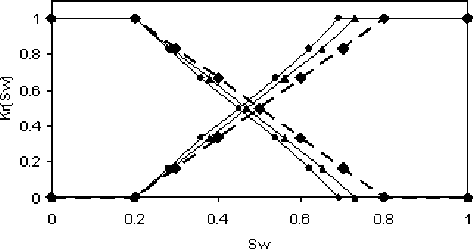
Рис. 2

На рис. 2 сплошными линиями нанесены расчётные зависимости составляющих тензора модифицированных ОФП kri 11 и kri22 (l = w, o) от средней водонасыщенности крупной ячейки Sw∗ (отмечены знаками соответственно А и •), а на рис. 3а, рис. 3б — соответствующие картины линий тока и распределение проницаемости, имитирующее глинистые включения в песчанике (отмечены чёрным цветом). Штриховыми линиями на рис. 2 для сравнения нанесены ОФП мелких ячеек-коллекторов. Как следует из рис. 2, модифицированные ОФП также имеют критические насыщенности Sw∗ , min и Sw∗ , max . Видно, что значения Sw∗ , min и Sw∗ , max для ОФП крупных ячеек ближе друг к другу, чем для ОФП мелких ячеек. Это смещение критических насыщенностей обусловлено наличием застойных зон, через которые не проходят линии тока. Величина смещения зависит от основного направления фильтрации.

ставить в виде

ϕ

= V jd^VV =

V

1 α_{V c}

ϕdV,

V c

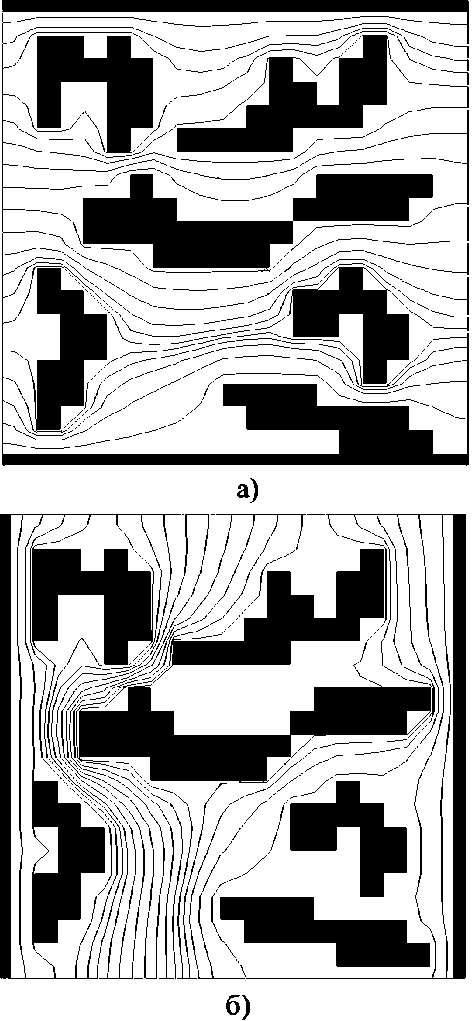
Рис. 3

∗∗

V S I =

"V | s i V^dV =

V

= ^aV d

| S l VdV +

V cd

1 α_{V c}

| S i vdV =

V c

1 αV cs

S l ϕdV.

V cs

Здесь первое и второе слагаемые в правой части выражения для ϕ S _l — соответственно подвижная и неподвижная часть порового объёма, занятого l -й фазой; a = VV — коэффициент песчанистости. После несложных преобразований это выражение можно привести к следующему виду:

S F = a _cd (S i } _d + (1 - a _cd ) (S i ) s ,       (14)

где α _cd — доля подвижного порового объёма коллектора, (S i ) d и (S i } s — средние насыщенности l -й фазы соответственно в подвижной и неподвижной частях коллектора. Тензорные величины α _cd , (S i ) d и (S i ) s определяются следующим образом:

ϕdV V cd ^{a cd} = J ^V’

V c

J S i vdV ^{( S} ‘ ' d = V T VdV-

V cd

J S l VdV ^- = T S V

V cs

Значения критических насыщенностей S _{w , min} и S _{w , max} определяются из (14) соответственно при

(S w ^ d

^{( S} w, min ) d ^и

(S w ) d

(S w, max ) d . Учи-

тывая, что при постоянных граничных условиях

^{( S} w ) s — ^(S w ⁽⁰⁾ ) s — ^(S w, min ) s — ^(S w, max ) s — Const,

выражения для S _{w , min} и S _{w , max} принимают вид

^S w, min    ^a cd ^{( S} w, min ) d ^{+ (1    a} cd ) ^{( S} w ) s ,

S W, max = a cd (S w, max ) d + (1 - a cd ) (S w ' s ,   (16)

Критические насыщенности для модифицированных ОФП можно получить из следующих соображений. Объем V крупной ячейки равен сумме объёмов коллектора и неколлектора. В свою очередь объём коллектора V _c разделяется на подвижный V _cd и неподвижный V _cs . При этом V _cd и V _cs являются тензорами и зависят от граничных условий, а V _c — скаляр. Находящаяся в коллекторе нефть также разделяется на подвижную и неподвижную. Учитывая, что пористость некол-лектора равна нулю, выражения (1) можно пред-

^{( S} w, min ) d

^{( S} w, max

) d

S w, min ϕdV V cd

J V^dV

V cd

S w, max ϕdV V cd

J V^dV

V cd

Таким образом, видно, что S _{w , min} и S _{w , max} зависят от начальных условий. Они зависят также и от граничных условий, поскольку согласно (15) от

них зависит подвижный объём. Однако они не зависят от вязкостей фаз. Для каждого направления значения S _w ^∗ _c и S _o ^∗ _r могут быть различными. Необходимо отметить, что при «открытых» граничных условиях S _w ^∗ _c и S _o ^∗ _r принимают меньшие значения, чем при «закрытых».

Подставляя (14) и (15) в (16) при начальных и граничных условиях соответственно (1) и S o ( x 1 ,x 2 , 0) = 1 — S _wc , с учётом того, что S o ( го ) = S or , для критических насыщенностей имеем следующие выражения:

(то есть шаровые части соответствующих тензоров) определяются следующим образом:

*         * _— *        *        * _— *

rw   r^w ⁽ w ) , roo   ro o ⁽ w ) ,

—

∗ S _w

∗∗ w__ wc

∗           ∗ ^.

^- wc ^- or

С помощью масштабирования можно получить

неплохое приближение для реальных ОФП, что

можно видеть из рис. 2 на примере линейных ОФП.

^S _w, min    ^a cd ^{( S} wc ) d ^{+ (1    a} cd ) ^{( S} w ) s ,

S W, max = a cd (1 — (S or ) d ) + (1 — a cd ) (S w ) s ,

(S wc ) d

S wc ϕdV

V cd

J ^dV

V cd

(S or ) d =

S or ϕdV

V cd

J v^dV

V cd

При адаптации гидродинамических моделей к истории разработки обычно варьируют параметры ОФП a i и b i ( l = w, o ) из (17). Ввиду сложной зависимости критических насыщенностей от многих отмеченных выше достаточно неопределённых факторов они обладают значительной степенью неопределённости. Поэтому при адаптации гидродинамических моделей, для которых up’scaling уже выполнен, необходимо оцени-

вать и варьировать также и критические насыщенности S _w ^∗ _c и S _o ^∗ _r . Их нижней оценкой являются величины

Отсюда следует, что при отмеченных условиях значения критической насыщенности воды для исходных и модифицированных ОФП одинаковы S W min = S w, min . Это подтверждается также приведёнными на рис. 2 численными расчётами.

В плане практического применения описанной выше методики можно отметить следующее. В коммерческих программных продуктах (Tempest MORE, ECLIPSE и др.) используются только изотропные ОФП. Для расширения области применения в этих программах можно производить масштабирование ОФП с использованием нормированной водонасыщенности:

(S wc ) = 4    dS wc dV, (S or ) = 4    dS or dV.

ϕ ^∗ V                     ϕ ^∗ V

V

V

—

—

S w = S w ( S w ) =

S w

S wc

S wc

S or

то есть наряду с k _rw = k _rw ( S _w ) можно производить расчёты и с k _rw = k _rw ( S _w ). Например, зависимости ОФП от водонасыщенности, полученные в результате исследований керна, часто представляются функциями вида

rw

— aw

( S w ) b

k ro = a o (1 — Si w ) b o

( a l b = const; l = w, o ) .           (17)

Для того чтобы в указанных выше программах учесть эффект смещения критических насыщенностей, из тензоров k _r ^∗ _l , S _w ^∗ _c и S _o ^∗ _r необходимо выделить шаровую часть:

Выводы. На основе развитой методики определения модифицированных ОФП установлено, что в неоднородном пласте при объединении мелких ячеек геологической сетки в крупные ячейки гидродинамической сетки (up’scaling) модифицированные ОФП являются тензорами, даже если ОФП мелких ячеек — скаляры.

Модифицированные ОФП крупных ячеек зависят не только от фильтрационно-ёмкостных параметров входящих в их состав мелких ячеек, но и от начального распределения насыщенностей фаз и направления фильтрационного потока в крупных ячейках, а также от условий на их границах. В частности, значения критических насыщенностей при «открытых» граничных условиях меньше, чем при «закрытых».

Использование модифицированных ОФП позволит избежать существующей в практике гидродинамического моделирования зависимости конечного КИН от степени огрубления геологической модели. Это может быть учтено изменением критических насыщенностей модифицированных ОФП, которые при адаптации модели к истории разработки в определённом диапазоне можно рассматривать в качестве свободных параметров.

*.     ¹    *          * ._._'i S * IfS *          *

k rl = 2⁽ k rl, 11 ⁺ k rl, 22 ) ,   S or = 2⁽ S or, 11 ⁺ S or, 22 ) ,

* =-( я*

S wc   2 ⁽ S wc, 11

+ S w ^* c, 22 ) ,

а затем применить масштабирование к модифицированным ОФП. Изотропные модифицированные нормированные ОФП и водонасыщенность