Расчёт и оптимизация режимов работы электрического привода газовой задвижки

Цитирование: Головенко Е. А. Расчёт и оптимизация режимов работы электрического привода газовой задвижки / Е. А. Головенко, Е. С. Кинёв, Е. А. Павлов, П. О. Шалаев, Е. Н. Лукьянов, А. В. Литовченко, К. А. Брызгова, Е. И. Помозов, А. А. Смирная // Журн. Сиб. федер. ун-та. Техника и технологии, 2025, 18(6). С. 845–856. EDN: UWTYJU

Синхронные двигатели с постоянными магнитами (СДПМ) известны своей высокой энергоэффективностью и компактностью. Это определяет возможности их применения в ограниченных пространствах и в условиях, требующих малого энергопотребления. Волновой редуктор, в свою очередь, обеспечивает значительное увеличение крутящего момента при небольших габаритах, что позволяет использовать его в сложных электромеханических системах. Векторное управление, реализуемое с помощью ПЧ, обеспечивает точное регулирование скорости и момента двигателя, что критически важно для управления оборудованием в реальном времени [1–2].

Одной из проблем, с которой сталкиваются инженеры, является обеспечение повышенной точности в регулировании контура положения. Это особенно актуально для технических комплексов, где требуется прецизионное управление положением механизма для предотвращения утечек, исключения перегрузок, возникновения аварийных ситуаций и общей безопасности оборудования. Кроме того, недостаточная точность управления может приводить к неэффективной работе системы и увеличению эксплуатационных затрат. Таким образом, системное исследование электромеханического комплекса с электроприводом должно быть направлено на изучение его возможностей, обеспечение преимуществ в контексте управления транспортом топлива. При системном представлении важно выявление потенциальных областей для совершенствования технологии и её внедрения в смежные промышленные объекты [3–4]. Особое внимание следует уделить решению проблемы точности при взаимодействии подсистем регулирования в разных контурах, что позволит значительно повысить надежность и эффективность работы электротехнического комплекса в целом [5–6]. Векторное управление является одним из наиболее эффективных методов управления электроприводами, в том числе в применении к трубопроводной арматуре. Помимо фундаментальных исследований в теории и практике управления встречаются отраслевые публикации, посвященные применению векторного управления. Например, компанией РэмТЭК построен электропривод с векторным управлением с акцентом на безопасность [7–8]. Указанные материалы посвящены обеспечению безопасности и надежности управления оборудованием трубопроводной арматуры в нефтехимической и газовой промышленности. Подчеркивается важность достижения высоких показателей, в стандарте безопасности интегрального уровня (SIL), для предотвращения аварий при эксплуатации оборудования [9–11]. На примере электропривода РэмТЕК-91, сертифицированного для использования в высокорисковых приложениях, показано соответствие уровню безопасности SIL 2. Одним из решений проблемы достижения точности позиционирования в автоматизированном электроприводе может выступать комбинированное управление, описанное в литературе [12–14]. Идеей рассмотренного метода является применение принципа инвариантности. Под комбинированным будем понимать алгоритмически формализованное сочетание управления, включающее в себя взаимосвязанное и взаимно обусловливающее управление по отклонению и по возмущающему воздействию. Помимо построения и исследования математической модели при комплексном исследовании целесообразно выполнять физическое моделирование [15–16]. Эксперимент проводят с применением электродвигателя, преобразователя частоты и модульной системы управления, в стендовом комплексе с привлечением проверенных сервисных программных средств с открытым программным кодом. Учитывая ограниченный объем статьи, совокупность результатов экспериментов при физическом моделировании, разработанном в проекте оборудования, здесь не представлена.

Описание результатов работы

Описание и исследование динамических процессов в системе управления выполняют по функциональной схеме, представленной на рис. 1. Согласно этой схеме генерируются математическая модель, а также схемная модель в выбранной системе моделирования.

Стенд для измерения характеристик электропривода показан на рис. 2.

Задание на движение, согласно схеме, электропривод получает в виде уставки положения. Регулятор положения обрабатывает управляющее воздействие, вычисляя текущую ошибку с фактическим положением и формируя управляющий сигнал для регулятора скорости. В свою очередь, регулятор скорости сравнивает требуемую частоту вращения с текущей, создавая опорный сигнал для регулятора тока. Сигнал по току в обратной связи преобразуется с помощью координатных преобразований Кларка (Clarke Transform) для исключения гармонической составляющей. Регулятор тока формирует компоненты для построения вектора напряжения. Используя обратные координатные преобразования, вектор напряжения транслируется в трехфазную систему и при помощи инвертора с широтно-импульсной модуляцией (ШИМ) подается на синхронный двигатель [17–18]. Скорость и момент двигателя уменьшаются и увеличиваются редуктором. Сигнал положения формируется датчиком, установленным на выходном звене редуктора. Блок коррекции Kp контура положения обе-

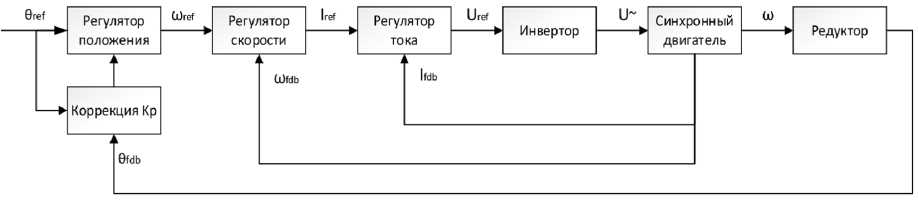
Рис. 1. Функциональная схема системы управления

Fig. 1. Functional diagram of the control system

Рис. 2. Стенды для измерения характеристик электроприводов

Fig. 2. Stands for measuring the characteristics of electric drives спечивает жесткость позиционирования в области малых отклонений заданной и фактической величины [19–20].

Для исследования автоматизированного комплекса следует кратко описать этапы построения математической модели системы управления. Перед описанием контуров регулирования можно показать уравнения, описывающие электромеханическое преобразование энергии в двигателе. Момент двигателя создается взаимодействием тока и потокосцепления статора. Учитывая фазность электродвигателя и число пар полюсов, он определяется произведением векторов.

Для модели трехфазного двигателя справедливо следующее выражение:

M — ~Z_pI_s x tp_s .

В проекции на оси dq получаем:

м = -Zp(ISd^d-lsq^q), где ^Pd и ^P d – потокосцепление статора по осям dq, Вб.

Потокосцепления определяются по следующим выражениям:

^d ~ ^Sd^Sd + ^f ^; ^q — Ls_qIsq ^.

С учетом этих выражений перепишем уравнение для момента в следующем виде:

M ⁼ 2^^p^^Sq^f ^ ^Sd^Sqdsd ^— ^Sq)) .

Пренебрегая магнитными потерями, уравнения равновесия статора СДПМ во вращающейся системе координат dq имеет следующий вид:

^Sd — I^Sd ~^~ + Rshd — ^SqIsq

^Sq = ^Sq “^ + ^Sq + ^^Sd^Sq + ^f

Выражая из системы ток, получаем:

^sd + ^Sqhq ~ Rshd)

1                                                    .

\~dt~ ^— L ^^{Sq —} ^^Sdhq ^— Rshq ^— ^^Pf}

Условие механического равновесия описывается выражением:

dw

J =M-MC.

dt

На основе полученных уравнений формируют структурную схему системы управления для СДПМ, показанную на рис. 3.

В общем случае контуры регулирования в векторной системе управления настраивают по-разному, с учетом текущих параметров быстродействия и перерегулирования. Контур тока включает составляющие d и q. Причем ток Iq управляет непосредственно моментом, а ток Id – магнитным потоком. При этом настраиваются они совместно под управлением алгоритма оценки технического оптимума. Таким образом обеспечивается наилучший переходный про-

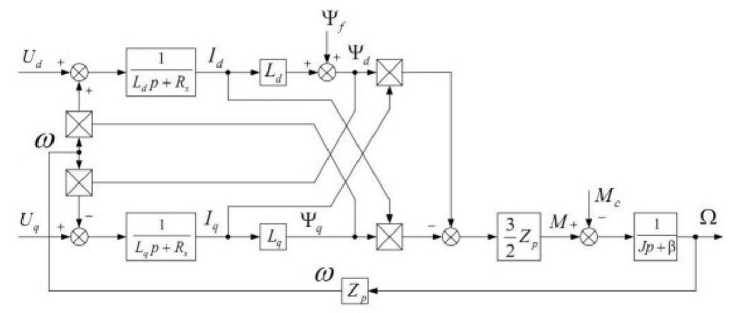
Рис. 3. Схема управления СДПМ в системе координат dq

Fig. 3. Control diagram of the PMSM in the dq coordinate system цесс с точки зрения перерегулирования, быстродействия и точности. В результате настройки получается ПИ регулятор с передаточной функцией вида:

W(p) =Kp* (1+—^—}, \ Ti * р/ где: Kp – пропорциональный коэффициент, Ti – интегральная постоянная времени.

Контур скорости строится над контуром тока Iq, так как он является моментообразующим и настраивается на симметричный оптимум. Это обеспечит наилучшее быстродействие, поскольку контур скорости по своей природе медленнее. После настройки в оптимум получается ПИ-регулятор такого же вида, как описано выше.

Контур положения строится над контуром скорости. Переходный процесс не должен содержать перерегулирования, так как применительно к трубопроводной арматуре нельзя допустить выезда запорного органа за пределы самой трубы. Ввиду чего приемлемым решением станет пропорциональный регулятор с простой передаточной функцией вида:

Иф) = Kp .

В рассматриваемом случае переходный процесс лишается астатизма, поскольку отсутствует компенсация ошибки. В данной статье предлагается решение в виде динамического управления коэффициентом передачи означенного пропорционального регулятора положения.

При движении в больших отклонениях контура положения регулятор большую часть движения находится в насыщении и не участвует в процессе. На таком участке регулирование режима осуществляет регулятор скорости. Когда же отклонение пути обеспечивает линейный режим регулятора положения, если оставить пропорциональный коэффициент неизменным, возникает существенная статическая ошибка. В ходе численных экспериментов можно попытаться установить значение коэффициента весьма большим, однако указанное вмешательство может повлечь возникновение повышенных пульсаций тока, а следовательно, и момента.

При переходе в линейный режим работы регулятора происходит увеличение коэффициента передачи пропорционального регулятора по мере приближения к заданному положению. Регулировочная характеристика для изложенного подхода представлена ниже, на рис. 4.

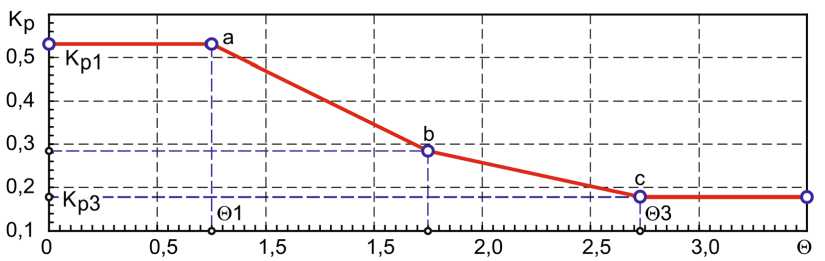
Рис. 4. Характеристика изменения Kp регулятора положения

Fig. 4. Characteristic of change of Kp of the position controller

По горизонтальной оси на графике показано отклонение в градусах выходного звена редуктора. Такое представление ограничивает дрейф точности приезда по длине пути повышенной протяженности. По вертикальной оси показаны интервалы значений коэффициентов передачи пропорционального регулятора для заданных отклонений. При движении к заданному положению система управления оценивает ошибку и генерирует значение соответствующего коэффициента. Если отклонение велико ^ref ^fdb ^ ^3 , то режим регулятора остается без корректировки. Как только отклонение становится равным ^ref ^fdb ^ ^3, возникает управляющее воздействие, запускающее коррекцию, в которой используется метод линейной интерполяции. Подобным образом происходит пересчет Kp, обеспечивая возможно малую ошибку управления по положению.

Реализацию математической модели, как правило, выполняют с применением средств моделирования. Вычислительный эксперимент проводят с учетом допущений и ограничений в программных средах, например MathLAB. Подходы к численному и физическому моделированию и особенностям проведения эксперимента достаточно подробно описаны в литературе [4–6]. При этом по степени соответствия результатов численного и физического эксперимента легко определить не только адекватность и точность сформированных моделей и методик. Использование основ системного анализа, рассмотренного в литературе [7–9], позволяет критически-рационально оценить предлагаемый подход.

При проведении численного исследования вначале следует убедиться в адекватности работы системы управления. С помощью программного комплекса MViewer удобно наблюдать и оценивать динамику параметров модели электропривода и параметров её режима. Запуск численного эксперимента выполняют симуляцией команды «Открыть» (кривая 1). При этом выполняют наблюдение за текущим положением компонентов модели (параметр B 2.7 CURR_ WAY) и заданной уставкой системы управления (B 2.5 REF_WAY). Графическое представление процесса открытия (кривая 2) в системе координат симулятора представлено на рис. 5.

По горизонтальной оси учитывается текущее относительное время. По вертикальной оси динамическая характеристика регулирования контура во внутренней системе координат симулятора.

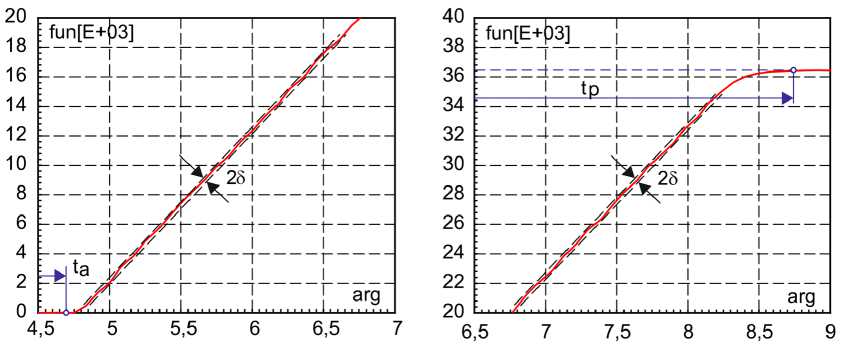
Пульсирующий характер процесса адаптации для нелинейного регулирующего воздействия несколько нагляднее отражается путём укрупненного представления двух фрагментов разорванной графической зависимости реакции системы (рис. 5), как показано на рис. 6 а , б .

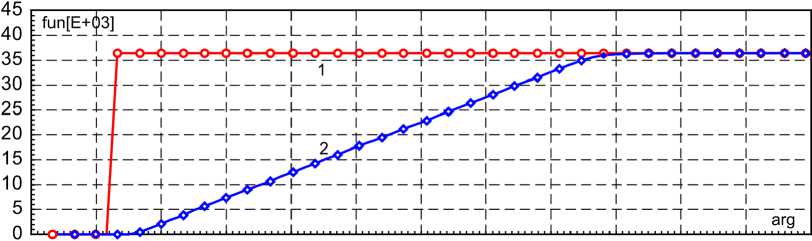
4     4,5     5     5,5     6     6,5     7     7,5     8     8,5     9     9,5     10

Рис. 5. Характеристики открытия задвижки трубопроводной арматуры

Fig. 5. Characteristics of opening of valve of pipeline fittings

б

б

Рис. 6. Укрупненный вид приезда в положение «Открыто»

Fig. 6. Enlarged view of arrival in the “Open” position

Несмотря на высокий порядок системы, переходный процесс близок к апериодическому, с временной задержкой ta, представлен прямой с пульсациями и сравнительно плавным выходом в установившийся режим tp. Двойная амплитуда 2δ динамических пульсаций не превышает значения 1,8 %. Это подтверждает корректную адаптацию системы управления при больших отклонениях в контуре скорости, а при малых – в контуре положения.

Аналогично моделируется поведение системы управления при побуждении движения (кривая 2) электромеханических узлов после старта (кривая 1) в противоположную сторону. Примеры характеристик численного моделирования показаны на рис. 7 и 8. Текущее время естественно сдвинуто на длительность установившегося состояния.

Полученный в эксперименте характер переходного процесса электромеханической системы аналогичен представленному на рис. 6. Судя по графикам, можно сделать вывод, что электропривод с векторным управлением в фиксированных границах отрабатывает управляющее воздействие с заданными требованиями качества.

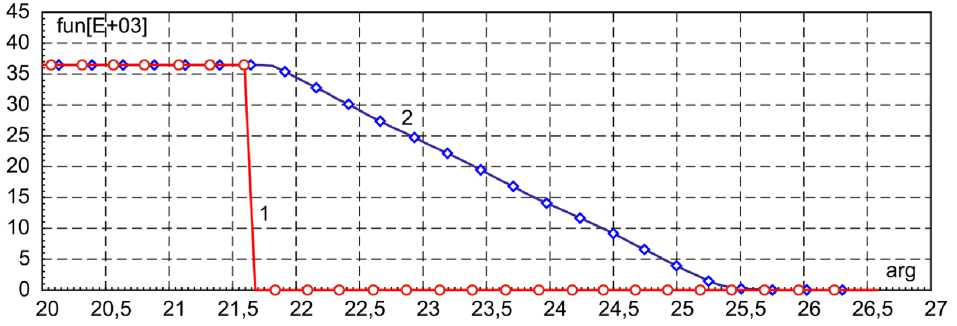
Рис. 7. Характеристики закрытия задвижки трубопроводной арматуры

Fig. 7. Closing characteristics of pipeline valves

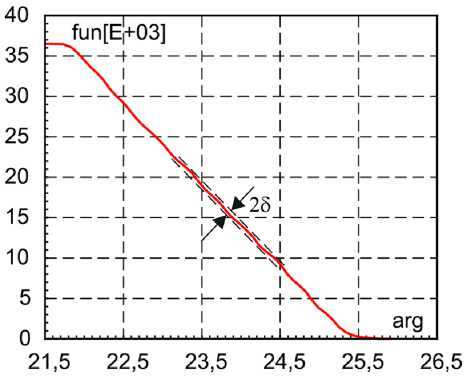
Рис. 8. Укрупненный фрагмент кривой приезда в положение «Закрыто»

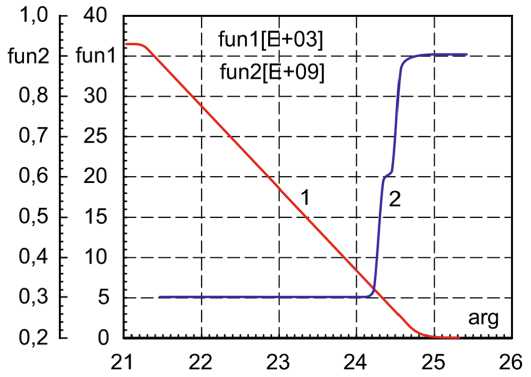
Рис. 9. Ошибка контура положения по протяжен- ности и изменение Kp

Fig. 8. Enlarged fragment of the arrival curve in the “Closed” position

Fig. 9. Error of the position contour along the length and change of Kp

Для оценки характеристик управления в системе подчиненного регулирования целесообразно рассмотрение процессов во внешнем контуре регулирования. Ниже на рис. 9 представлен график изменения Kp по мере приближения к заданному положению.

Кривая 1 на графике приближенно иллюстрирует процесс завершения движения. По мере снижения отклонения положения (кривая 2) регулятора коэффициент передачи его звена возрастает, в соответствии с характеристикой, показанной на рис. 4.

Выводы

Проведенное исследование подтвердило эффективность применения адаптивного управления в электроприводах трубопроводной арматуры на основе синхронного двигателя с постоянными магнитами и волновым редуктором. Предложенный метод динамической коррекции коэффициента передачи пропорционального регулятора положения (Kp) позволил существенно снизить статическую ошибку позиционирования, исключить перерегулирование, что критически важно для обеспечения безопасности и надежности работы систем транспортировки – 853 – жидкостей и газов. Реализация векторного управления с подчиненными контурами тока, скорости и положения, а также адаптация параметров регулятора в зависимости от текущего отклонения, обеспечили высокую точность управления, как на этапе крупных перемещений, так и в зоне малых ошибок. Важным достижением стало устранение компромисса между жесткостью позиционирования и энергоэффективностью. Динамическое увеличение Kp при приближении к заданному положению позволило адаптировать систему управления, сохранив плавность переходных процессов во избежание перегрузок, характерных для регулирующих узлов с фиксированными коэффициентами. Внедрение разработанного подхода в промышленность может повысить надежность трубопроводных систем, сократить эксплуатационные затраты и снизить риск аварийных ситуаций.