Расчёт интерференционной картины, формируемой переносящими изображения световыми пучками после дифракции на акустической волне в одноосном кристалле

Оптическая когерентная микроскопия (ОКМ) с регистрацией в спектральной области (ОКМ СО) в настоящее время широко используется для неинвазивной диагностики биологических объектов (например, в офтальмологии и дерматологии) и неразрушающего контроля технических изделий и материалов (например, при анализе деформаций и дефектоскопии) [1, 2]. Этот метод позволяет получить распределение коэффициента отражения по глубине образца путем пересчета спектральной зависимости интенсивности света на фотоприемнике, измеренной при перестройке рабочей длины волны интерферометра.

ОКМ СО выгодно отличают отсутствие подвижных частей, возможность работы в полном поле, высокая производительность и другие достоинства [3]. Для спектральной перестройки в методе ОКМ СО используется либо перестраиваемый в широком диапазоне длин волн источник света и последовательная во времени регистрация спектральных изображений [4], либо широкополосный источник света с пространственным разложением в спектр сигнала на выходе интерферометра и регистрация его линейкой фотоприемников [5]. Еще одним вариантом реализации спектральной перестройки является акустооптическая (АО) фильтрация интерферирующих световых пучков, переносящих изображения, в выходном канале интерферометра [6]. Как показано в [7], этот подход позволяет создавать мультимодальные аналитические системы, так как допускает исследование объекта не только в режиме ОКМ, но и методами широкополосной (световой) и спектральной микроскопии. Такие мультимодальные системы необходимы при изучении динамических процессов и в случаях, когда перемещение исследуемого объекта с одной установки на другую для последовательного анализа не представляется возможным.

В системах ОКМ СО с АО-фильтрацией на выходе интерферометра используется широкополосный источник излучения, из спектра которого АО-монохроматором выделяется узкая спектральная составляющая. Ширина δλ этой составляющей определяет длину когерентности λ 0 ²/δλ (λ 0 – рабочая длина волны интерферометра). Применение широкополосного источника позволяет избежать спекл-шумов в интерферограммах в отличие от схем ОКМ СО на основе перестраиваемых лазерных источников высококогерентного излучения.

Для реализации такого подхода АО-фильтрация одновременно опорного и объектного световых пучков не должна искажать интерференционную картину. Амплитудные и пространственно-спектральные искажения, сдвиг частоты, объемность взаимодействия, расходимость, снос, переотражения звуковой волны и другие особенности АО-дифракции [8, 9] накладывают ограничения на качество передаваемого изображения [10, 11] и требуют учета при проектировании систем ОКМ СО на ее основе.

В настоящей работе впервые проведен теоретический расчет интерференционной картины, формируемой двумя световыми пучками, переносящими изображения, после их брэгговской дифракции на одной акустической волне в одноосном кристалле.

Оптическая схема

Схема ОКМ СО со спектральной фильтрацией интерферирующих пучков, переносящих изображения, представляет собой интерферометр Майкельсона с АО-монохроматором в выходном канале (рис. 1). В ней излучение широкополосного источника 1 коллимируется объективом 2, делится светоделителем 3 и направляется в опорное и объектное плечи интерферометра. Микрообъективы 4 фокусируют излучение на плоском зеркале 5 и исследуемом образце 6, затем собирают его после отражения от 5 и 6, формируя опорный и объектный пучки. Эти пучки сводятся вместе светоделителем 3 и направляются в приемный канал, где осуществляется их спектральная фильтрация АО-монохроматором 7 и фокусировка объективом 8 на матричном приемнике излучения 9. Для восстановления трехмерной структуры исследуемого образца производится перестройка монохроматора по длине волны λ0 и запись серии спектральных интерференционных изображений Iλ0(x, y).

АО-монохроматор 7 содержит АО-ячейку, представляющую собой кристалл, и два скрещенных поляризатора, между которыми она расположена. В АО-ячейке пьезопреобразователем возбуждается ультразвуковая волна частотой f , на которой линейно поляризованный световой пучок дифрагирует с изменением направления поляризации на ортогональную. Не-дифрагированное излучение отрезается выходным поляризатором. Центральная длина волны полосы пропускания АО-ячейки λ 0 связана с частотой ультразвука f как [10]:

Хо = F ( 9, Y ) V A n/f , (1) где v – скорость ультразвука; ∆ n = n e – n o – разность показателей преломления для обыкновенно ( n o ) и необыкновенно ( n e ) поляризованных волн; F (θ, γ) – коэффициент, зависящий от геометрии АО-взаимодействия (ориентации световой θ и звуковой волн γ).

Для получения интерференционных изображений на различных длинах волн λ 0 на пьезопреобразователь последовательно подаются соответствующие им частоты управляющего сигнала f .

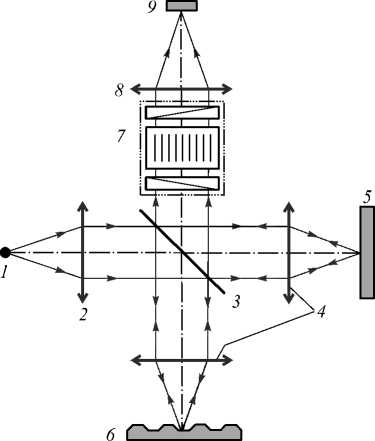
Рис. 1. Схема интерферометра Майкельсона с АО-фильтрацией интерферирующих пучков, переносящих изображения, в приемном канале

Расчет интерференционной картины

В интерферометре Майкельсона интенсивность интерференционной картины, образованной опорной и объектной волнами с выделяемым АО-монохроматором узкополосным (квазимонохромати-ческим) спектром излучения S(k) (k = 2π/λ – волновое число), максимум которого приходится на длину волны λ0 = 2π/k0, описывается выражением:

I ( x , y ) = 1 1 ( x , y ) + 1 2 ( x , y ) +

+2^I! (x,y)12 (x,y)V(A(x,y))cos(k0A(x,y)), где I1(x, y), I2(x, y) – распределение интенсивности, создаваемое пучками из опорного и объектного каналов. Оптическая разность хода ∆(x, y) неоднородна по сечению светового пучка и определяется разностью оптических длин объектного LS(x, y) и опорного LR(x, y) плеч:

A ( x , y ) = 2 [ L r ( x , y ) - L s ( x , y ) ] .                   (3)

Оптическая длина объектного плеча L S ( x , y ) в случае отражающих непрозрачных объектов описывает их геометрический профиль. Ширина интерференционных полос определяется длиной волны излучения λ 0 и углом сведения интерферирующих волн. Для получения интерференционных полос конечной ширины плоское зеркало в опорном плече наклоняют на небольшие углы α и β вокруг осей x и y [12]:

L R ( x , y ) = L₀ + a x + в y + z_R ,

где L 0 – оптическая длина пути, одинаковая для обоих плеч, z R – начальное смещение опорного зеркала вдоль оптической оси, которое вводится в схему для того, чтобы избежать наложения автокорелляцион-ных составляющих обратного преобразования Фурье на полезный сигнал [13].

Функция видности V , служащая мерой контраста интерференционных полос и являющаяся одним из основных показателей качества интерференционной картины, определяется формой спектра регистрируемого излучения S ( k ) и может быть рассчитана по формуле [14]:

V ( A ( x , y ) ) =

J S ( k ) exp ( ik A ( x, y ) ) d k

J! S ( ^k ) dk

где S ( k ) = S 0 ( k ) T ( k ); S 0 ( k ) – спектр излучения источника света; T ( k ) – функция пропускания АО-фильтра, задаваемая выражением [8]:

T = ( Г L ) ²

sin ² f L J Г ² + ( A k /2 ) 2 ' у 2

I L ^Г² + ( A k /2 ) 2 I

где L – длина АО-взаимодействия, определяется длиной пьезопреобразователя; параметр Г ~ рР зависит от мощности ультразвуковой волны P и для достижения 100 % эффективности дифракции мощность устанавливается из условия Г L = п /2; A k - волновая расстройка.

Ненулевая волновая расстройка ∆k неизбежно возникает при АО-фильтрации световых пучков в пределах поля зрения оптической системы, предшествующей АО-монохроматору. Это объясняется тем, что условию Брэгга (синхронизма) ki+q = kd (ki, kd – волновые векторы падающей и дифрагированной волн, q – волновой вектор акустической волны) точно удовлетворяет только луч, идущий из центра поля зрения в направлении синхронизма θ1 = θs1, θ2 = θs2. Остальные лучи имеют ненулевую волновую расстройку А к, которая для геометрии дифракции е^о задается формулой [11]:

А к = кп о I ^ ( 9 1 ) - п ) + 2 П^ ( 9 1 )( 1 - A ) - 1 1 , (7)

где A =cos(01—Y1) — cos 91cos Y1(1-cos(02-Y2)); Y1, Y2 — уг— лы распространения акустической волны q; η = λ0/(Λno) – безразмерный спектральный параметр, определяющий связь длин волн света λ0 и звука Λ; ^ (91) = ^0 / Jcos2 91 + ^0 sin2 91 ; ^o = neno. Аналогич ные формулы для случая дифракции o^e получены в [15]. Наличие волновой расстройки ∆k ≠ 0 для всех направлений, кроме одного (θ1 = θs1, θ2 = θs2), удовлетворяющего условию синхронизма, приводит к тому, что функция пропускания Т приобретает зависимость от пространственных координат (x, y), что необходимо учитывать при вычислении видности V. Вид функции пропускания Т(θ1, θ2) АО-монохроматора существенно зависит от геометрии АО-взаимодействия.

Следует отметить, что для передачи изображений, как правило, используется широкоугольная геометрия АО-взаимодействия в полярной плоскости Y =0, для которой θ 2 = γ 2 =0 (рис. 2). В этом случае углы распространения света θ 1 и звука γ 1 однозначно связаны между собой [10].

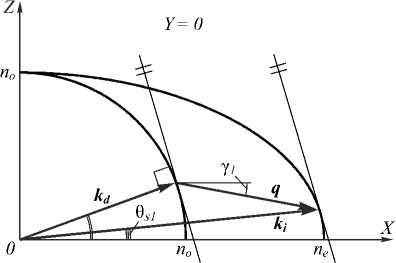
Рис. 2. Волновая диаграмма широкоугольного АО-взаимодействия в полярной плоскости

Ширина функции пропускания АО-фильтра δλ, выраженная в единицах длины волны, зависит от выделяемой длины волны λ 0 [9]:

SX = ^ 0 F ( 9, y )/ L А п . (8)

С учетом зависимости функции пропускания T АО монохроматора от пространственных координат ( x , y ) и от выделяемой длины волны λ 0 = 2π/ k 0 выражение (5) для функции видности принимает вид:

V ( А ( x , у ) , к о ) =

J S ₀ ( к ) T ( к , к ₀, x , у ) exp ( ik А ( x , у ) ) d к J -^ S о ( к ) T ( к , к о , x , у ) d к

.

Совокупность формул (2)–(9) позволяет рассчитать интерференционную картину I λ0 ( x , y ) в схеме интерферометра Майкельсона с АО-фильтрацией интерферирующих пучков в приемном канале.

Экспериментальная установка

Для проверки результатов моделирования на базе интерферометра Линника МИИ-4 была собрана экспериментальная установка по схеме, показанной на рис. 1. В качестве широкополосного источника использовалась галогенная лампа. В приемном канале был установлен монохроматор на основе широкоугольной АО-ячейки (θ 1 = 73,6°, γ 1 = –7,1°, θ 2 = γ 2 =0°) из одноосного кристалла TeO 2 . Основные параметры монохроматора: диапазон перестройки – 450-750 нм, угловая апертура – 3º×3º, длина преобразователя – L = 12 мм.

Для иллюстрации на рис. 3 представлены спектр излучения используемого источника S (λ) и функция пропускания АО-монохроматора Т (λ) при настройке его на различные длины волн λ 0 , а на рис. 4 – вычисленные по формуле (9) зависимости видности интерференционной картины V от оптической разности хода ∆ для тех же длин волн λ 0 . Как показывает расчет, с увеличением длины волны λ 0 видность, в значительной степени определяющая качество интерференционной картины, снижается.

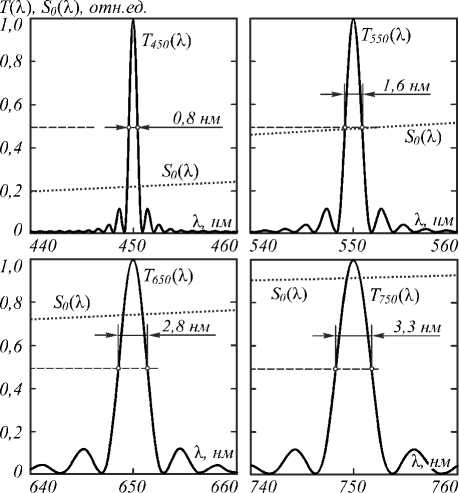
Рис. 3. Нормированные спектр излучения используемого источника света S 0 (λ) и функция пропускания АО-фильтра Т λ0 (λ)

Эксперимент

В качестве тест-объекта для моделирования и экспериментов использовалась мира с прямоугольным профилем с периодом 100 мкм и высотой h =9,7 мкм (рис. 5 а ). Начальное смещение опорного зеркала z R =25 мкм, углы наклона опорного зеркала α = 0,3°, β = 0,7°. Ввиду малости углов α и β в сравнении с угловой апертурой АО-фильтра функция пропускания

АО фильтра Т для опорного и объектного интерферирующих пучков принималась одинаковой.

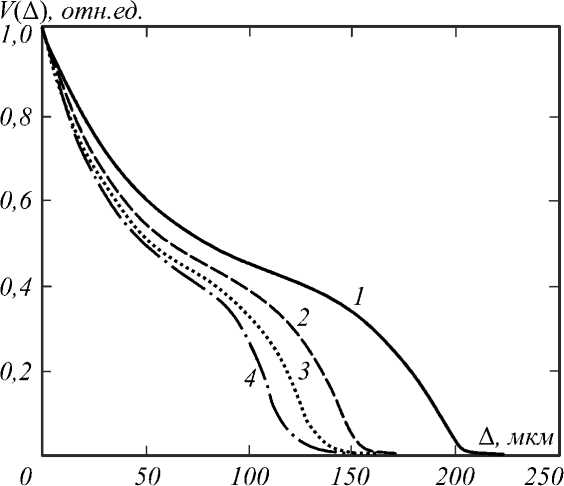
Рис. 4. Теоретическая зависимость видности V интерференционной картины от оптической разности хода ∆ при настройке фильтра на длину волны 450 нм (1), 550 нм (2), 650 нм (3), 750 нм (4)

б)

100 мкм

а)

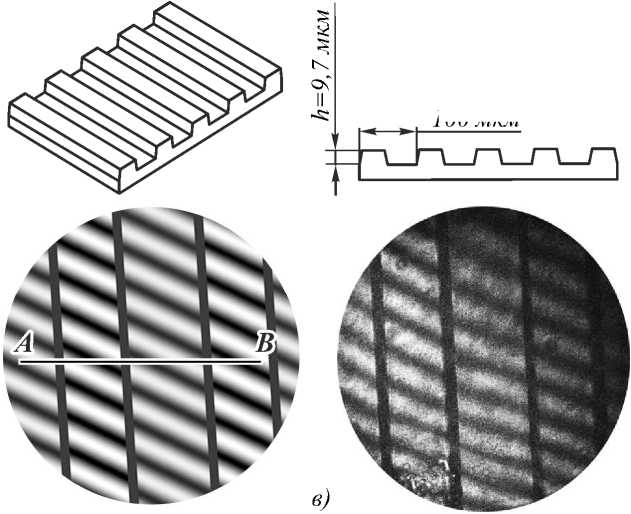
Рис. 5. Исследуемый объект (а), смоделированное (б) и экспериментально полученное (в)

интерференционные изображения на длине волны λ 0 = 550 нм

На рис. 5 б , в представлены два интерференционных изображения миры на длине волны 550 нм: рассчитанное согласно (2)–(9) и экспериментально полученное. Вертикальные темные полосы соответствуют наклонным боковым граням ступенек миры, так как отраженное от них излучение не попадает в апертуру микрообъектива. При расчете не учитывались аберрации оптической системы, хроматические аберрации АО-фильтра и шумы изображения, что обуславливает некоторое отличие расчетного и экспериментального изображений.

На рис. 6 сопоставлены профили поверхности тест-объекта, вычисленные вдоль отрезка АВ (рис. 5 б ) в результате обработки серии из 300 спектральных интерферограмм в диапазоне 450–750 нм с постоянным шагом по частоте λ^–1: синтезированных расчетным путем (сверху) и экспериментально полученных (снизу). Обработка данных заключалась в вычислении вертикального профиля коэффициента отражения

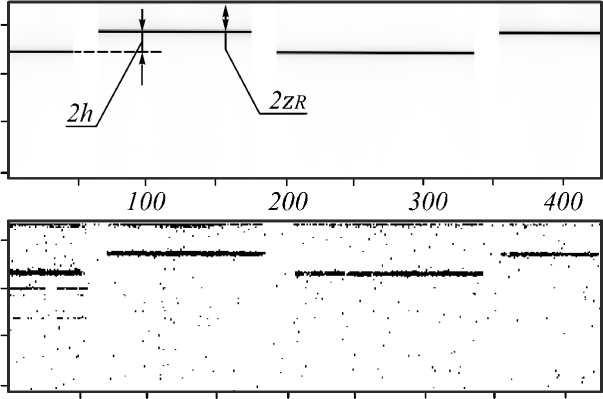
света в каждой точке отрезка AB путем применения обратного преобразования Фурье к спектральным зависимостям интенсивности I ( k ).

Z, мкм

100       200       300       400

Координата вдоль линии АВ, мкм

Рис. 6. Вычисленные в результате численного моделирования (сверху) и по данным экспериментального измерения (снизу) профили тест-объекта

Заключение

В настоящей работе впервые приведены основные соотношения для вычисления интерференционной картины, формируемой световыми пучками, переносящими изображения, после их спектральной АО-фильтрации. Показано, что характеристики АО-фильтра влияют непосредственно на качество интерференционной картины и должны быть учтены при ее расчете. Так, например, контраст интерференционных полос (видность) этой картины определяется функцией пропускания фильтра Т (θ 1 , θ 2 , λ), которая зависит от геометрии АО-взаимодействия (углов распространения света θ и звука γ, длины L акустоопти-ческого взаимодействия). Результаты теоретического расчета подтверждаются данными экспериментов.

Интерференционные схемы на основе АО-фильтрации излучения в приемном канале выгодно отличают устойчивость к внешним засветкам, программное управление, произвольная спектральная адресация и другие достоинства. При соответствующей доработке представленного аналитического описания формирования интерферограмм указанный подход может найти применение не только в схемах ОКМ СО, но и в схемах цифровой голографической микроскопии и других интерференционных системах для анализа амплитудно-фазовой структуры объектов.

Работа выполнена при поддержке грантов Президента МК-199.2017.8 и РФФИ 16-07-00393.