Расчёт оптических элементов, работающих по принципу полного внутреннего отражения и формирующих заданные световые распределения в круглых областях

В настоящее время светодиодные источники излучения занимают всё большую и большую часть российского рынка. Одной из наиболее наукоёмких частей светодиодного светотехнического устройства является вторичная оптика – оптические элементы, преломляющие световой поток от источника и направляющие его в заданную область. Расчёт таких оптических элементов даже в приближении точечного источника излучения и одной преломляющей поверхности сводится к решению нелинейного дифференциального уравнения в частных производных типа уравнения Монже–Ампера [1], что является крайне сложной задачей.

В случае формирования узкоугольных распределений освещённости с угловым размером менее 50–60° используется так называемая TIR-оптика, или оптика, работающая по принципу полного внутреннего отражения. Такие оптические элементы имеют достаточно сложную конструкцию. Как правило, они содержат внутреннюю поверхность, через которую лучи от источника попадают внутрь оптического элемента, боковую поверхность, на которой боковые лучи испытывают полное внутреннее отражение и поворачиваются на большие углы порядка 60–90°, и верхнюю внешнюю поверхность, через которую лучи выходят из оптического элемента.

Для расчёта TIR-оптики, как правило, используются различные итерационные методы, позволяющие оптимизировать форму преломляющих поверхностей из условия формирования заданного светового распределения [2–7]. Успех работы любого оптимизационного метода зависит от начального приближения. В данной работе задача расчёта таких оптических элементов в приближении точечного источника излучения сведена к интегрированию диф- ференциальных уравнений первого порядка, разрешённых относительно производных. Соответствующие дифференциальные уравнения получены для случая расчёта оптического элемента с плоской внешней поверхностью, когда формирование заданного светового распределения осуществляется за счёт внутренней поверхности, а также для случая расчёта оптического элемента с внутренней коллимирующей и внешней асферической поверхностями. Рассчитаны оптические элементы, формирующие распределения освещённости и интенсивности с эффективностью более 90 % и неравномерностью светового распределения менее 4 %. Кроме того, получена и исследована зависимость неравномерности формируемого светового распределения от размера источника излучения.

1. Метод расчёта TIR-оптики с плоской внешней поверхностью

Рассмотрим задачу формирования заданного радиально-симметричного узкоугольного светового распределения от точечного источника излучения с интенсивностью 1 0 ( Р ) , где в - зенитный угол сферической системы координат. Под узкоугольным световым распределением будем подразумевать распределение интенсивности I ( в ) или освещённости E ( r ) , отличное от нуля только в области малых угловых размеров в = arctan( r / f ) е [ 0, в max ] , где r -радиальная координата цилиндрической системы координат с осью Oz , f – расстояние от источника до выходной плоскости, а P _max - угол, определяющий размеры освещаемой области и не превышающий 40 - 50 ° .

Для формирования таких световых распределений предлагается использовать конструкцию оптического элемента, изображённую на рис. 1.

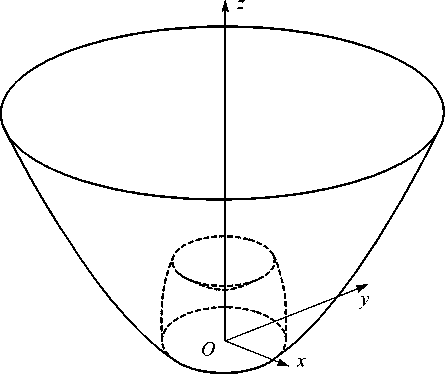
Рис. 1. Конструкция оптического элемента с плоской внешней поверхностью

Представленный оптический элемент является телом вращения, полученным путём вращения профиля, изображенного на рис. 2, вокруг оси Oz . Часть ( а ) профиля преобразует сферический пучок от источника излучения, расположенного в начале координат, и формирует заданное световое распределение. Часть ( b ) создаёт удалённый мнимый источник излучения в точке M , уменьшая таким образом угловой размер пучка, падающего на часть профиля ( с ). Часть профиля ( с ) работает по принципу полного внутреннего отражения и, как и часть ( а ), формирует заданное световое распределение.

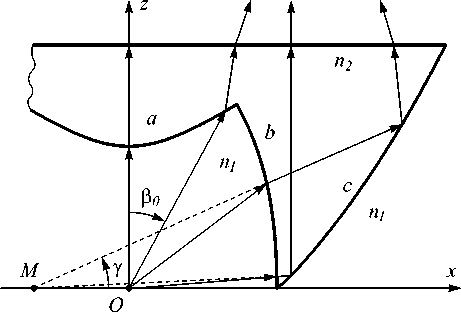
Рис. 2. Профиль оптического элемента с плоской внешней поверхностью

Рассмотрим расчёт частей профиля ( а ), ( b ) и ( с ). Для нахождения кривой ( а ) необходимо записать дифференциальное уравнение для её радиус-вектора [8]:

d Г а ( в о ) = _ r _{( в} )       Sin ( в о +в а ( в о ) )

d ^e 0         a 0 ( n 2/ n i ^_ cos ( ^в о ^+в а ( ^в о ) ) )

где в _о и в _а ( в _о ) — угловые координаты соответственно падающего и преломлённого на поверхности ( a ) лучей.

Поверхность ( b ), формирующая мнимый источник излучения в точке M , определяется исходя из принципа Ферма. Запишем функцию эйконала на окружности с центром в точке мнимого источника:

r ( в ) n — n 2 r 2 ( в ) + 1 ² + 2 Г ь ( в ) 1 ² sin в = Т о , (2)

где r b ( в ) — функция длины радиус-вектора части ( b ) профиля, а l – расстояние между реальным и мнимым источниками. Уравнение (2) представляет собой квадратное уравнение относительно длины радиус-вектора r_b ( в ) , коэффициенты которого зависят от параметров n 1 , n ₂, Т _о и 1 .

Профиль поверхности ( с ), работающей по принципу полного внутреннего отражения, рассчитывается по формуле [9]

drc (y)             п/2 Y в, (y)

— = г , ( г ) c.g----- 2----- ,

где у - угол между лучом, падающим на поверхность ( с ), и осью Ox , а в , (y) — угловая координата отражённого луча.

Необходимо отметить, что, так как поверхность ( с ) работает по принципу полного внутреннего отражения, на угловые координаты y и в , ( y) накладывается следующее ограничение:

П 2 + Y_в , (y)

потоку, проходящему после оптического элемента через соответствующий элементарный телесный угол d Q = 2п sin P d P . Запишем этот закон в дифференциальной форме:

2пI0 (Р0) sinP0dP0 = 2nI(Р) sinPdP , и Рc (y) определяются, как и в пункте 1.1, из закона сохранения светового потока. В этом случае закон сохранения светового потока записывается следующим образом:

2п10 (Р0) sin P0dP0 = 2nE0 (r) rdr, или или

d P = I о ( P o ) ^sin P o d P o      I ( P ) sin P ’

d r = T ₁( ^p0) sin ^p 0 ^{d P} 0       ^E 0 ( ^r ) ^r

здесь P _o - угловая координата луча до преломления на внутренней поверхности оптического элемента, а Р - его угловая координата после выхода из оптического элемента.

В случае ламбертовского источника излучения и требуемого равномерного распределения интенсивности ( I ( Р ) = I ) зависимость Р ( Р ₀ ) для центральной части ( a ) профиля оптического элемента может быть получена из уравнения (5) в аналитическом виде:

где E ₀ ( r ) - требуемое распределение освещённости в выходной плоскости.

В случае ламбертовского источника и равномерного распределения освещённости решение уравнения (10) для части ( a ) поверхности может быть получено в аналитическом виде:

r ( P 0 ) = R

sin P0

sin ^P 0max

Р ( Р ₀ ) = arccos I 1 - ( 1 - cos2 P ₀ )

I cosl'L x )

^{1 - COs2 P} 0max j

здесь P _0max - угол, определяющий границу между частями ( а ) и ( b ) преломляющей поверхности. Угловая координата луча Р a ( Р ₀ ) до преломления на верхней плоской поверхности рассчитывается по закону Снеллиуса:

где R – радиус освещаемого круга. С учётом выражения (11) и геометрии задачи угловая координата луча внутри оптического элемента Р _а ( Р ₀ ) рассчитывается следующим образом:

^P a ( ^P 0 ) = arcsin

n

¹ sin arctan n ₂

R sin P ₀

^f sin ^P 0max

I n

^Р а ( ^Р 0 ) = arcsin I —sin ^Р ( ^Р 0 )

V n 2

Аналогично, записав закон сохранения светового потока для части ( c ) поверхности, получим зависимость r (y) :

Выражение для функции лучевого соответствия Р c ( у ) также может быть получено в аналитическом виде в случае ламбертовского источника излучения и равномерного распределения интенсивности:

r (y) = R^	1 - sin2 P 0 (y)
	1 - sin2 P 0max

где

^Р c (y) =

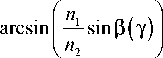
P(y) = arccos I 1 -

IzcosP moL cos^{2 P} 0max

cos2

^P 0 (y) j .

Выражения (1)–(5) содержат три дифференциальных уравнения первого порядка, разрешённых относительно производных, и позволяют путём численного интегрирования (например, методом Рунге– Кутты) рассчитать профиль оптического элемента, формирующего заданное распределение интенсивности в круглой области при точечном источнике излучения.

1.2. Нахождение функций лучевого соответствия в случае формирования заданного распределения освещённости

При формировании заданного распределения освещённости функции лучевого соответствия Р a ( Р ₀ )

Функция лучевого соответствия P _c (y) определяется из геометрических соображений и равна

P c (y) = arcsin

П ■ ₊ f ^r (y) — sin arctan I---- n 2          V f

Как и в случае формирования заданного распределения интенсивности, решение задачи формирования заданного распределения освещённости сводится к численному интегрированию трёх независимых дифференциальных уравнений первого порядка (1), (3) и (10), разрешённых относительно производных.

2. Метод расчёта TIR-оптики с асферической внешней поверхностью

В пункте 1 для управления световым потоком использовался внутренний профиль, состоящий из частей ( a ), ( b ) и ( c ), а верхняя поверхность оптического элемента считалась плоской. В некоторых случаях удобно, чтобы внутренняя поверхность TIR-оптики была коллимирующей, а управление световым потоком осуществлялось с помощью внешней поверхности. Рассмотрим расчёт внешней поверх-

ности из условия формирования заданного радиально-симметричного распределения освещённости E 0 ( r ) в плоскости z = f при коллимирующей внутренней поверхности.

Форма внешней поверхности однозначно определяется её профилем z ( р ) . Получим дифференциальное уравнение первого порядка, разрешённое относительно производной d z /d p для расчёта этого профиля.

Производная d z /d p численно равна отношению - n_p jn_z компонент единичного вектора нормали к профилю. Выразим единичный вектор нормали в виде линейной комбинации единичных векторов падающего и преломлённого лучей:

n = с _o a _o + c ^. (15)

Умножив векторно обе части уравнения (15) на n , получим равенство

С 0 [ a o , n ] = - C [ a i , n ] • (16)

Сравнив равенство (16) с законом Снеллиуса, найдём отношение коэффициентов c1 /с0 = -1 n , где n – показатель преломления оптического элемента. Приняв во внимание тот факт, что вектор n является единичным, получим, что n =

n ai - 1 ao n2

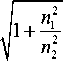
^{- 2} ~ ( a o , a i ) n ₂

Зная единичный вектор нормали n , несложно записать дифференциальное уравнение для профиля внешней преломляющей поверхности:

dz =    aip     = dp   ni/n2 - aiz

= r ( p ) ^- P ⁽ⁱ 8) n 2 hi J ( r ( p ) ^- p ) 2 ⁺ ( f ^- z ( p ) ) 2 ^- ( f ^- z ( p ) )

Правая часть уравнения (18) зависит только от координаты p и функции z ( p ) , поэтому оно может быть численно проинтегрировано любым стандартным способом (например, с помощью метода Рунге– Кутта).

Функция лучевого соответствия r ( p ) , входящая в уравнение (18) и определяющая зависимость координаты r луча в выходной плоскости от его координаты p в плоскости перед преломляющей поверхностью, может быть найдена из закона сохранения светового потока аналогично пунктам 1.1 и 1.2. В данном случае закон сохранения светового потока записывается следующим образом:

E '( p ) 2 np d p = E _o ( r ) 2 n r d r , (i9)

где E‘(p) - распределение освещённости в плоско сти перед верхней поверхностью, а Eo (r) - требуемое распределение освещённости в выходной плоскости. Функцию освещённости E‘(po) можно считать известной, так как известна форма коллимирующих профилей (a), (b) и (c).

В случае равномерного распределения освещённости в выходной плоскости функция лучевого соответствия r (p) явно выражается из (i9) как r (p) = R

( p              V/²

J E Ш d t tx.--------

J E '(Уб d t

• V o               J

  
  

• 3. Примеры расчёта оптических элементов

где ρ_max – радиус оптического элемента, а R – радиус освещаемой области в выходной плоскости.

Представленные выше методы расчёта оптических элементов были реализованы на языке программирования Matlab. Ниже приведены результаты расчёта и моделирования оптических элементов, формирующих типовые распределения освещённости.

В качестве примера с помощью выражений (1)– (3), (5) был рассчитан оптический элемент, формирующий диаграмму направленности с полным угловым размером 40°. Профиль оптического элемента изображён на рис. 3. Показатель преломления материала оптического элемента считался равным 1,5.

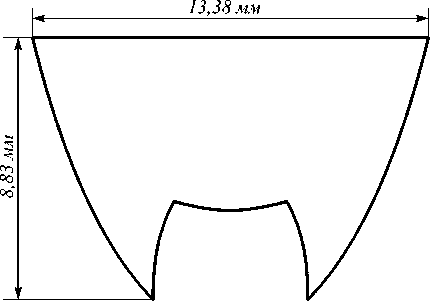
Рис. 3. Профиль оптического элемента, формирующего равномерное распределение интенсивности с угловым размером 40°

На рис. 4 приведено промоделированное распределение интенсивности, формируемое рассчитанным оптическим элементом. Размер формируемого распределения интенсивности равен 40°, а тип распределения интенсивности соответствует равномерному.

На рис. 5 изображён оптический элемент, рассчитанный с помощью метода (1)–(3), (10) и формирующий равномерное распределение освещённости в круге с радиусом 400 мм на расстоянии 1000 мм от точечного ламбертовского источника излучения. Как и в предыдущем случае, при расчёте, показатель преломления оптического элемента был принят 1,5, а угол β0max равным 30°.

Распределение освещённости, формируемое рассчитанным оптическим элементом, показано на рис. 6. Световая эффективность оптического элемента составляет 92,0 %, а относительное среднеквадратичное отклонение (СКО) формируемого распределения освещённости от равномерного – менее 5 %.

ляет 5,8 %, а световая эффективность оптического элемента равна 90 %.

Сравнение распределений освещённости на рис. 6 и рис. 8 показывает, что использование плоской внешней поверхности оптического элемента позволя- ет достичь световых характеристик не хуже, чем использование асферической поверхности, при меньших габаритных размерах оптического элемента.

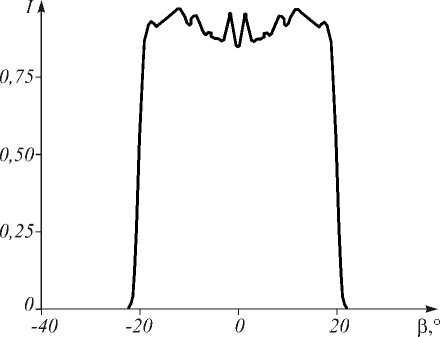
Рис. 4. Распределение интенсивности, формируемое

V, vM

О

-200

-400

-400 -200    0    200   400

Рис. 5. Профиль оптического элемента, формирующего равномерное распределение освещённости в круге с радиусом 400 мм

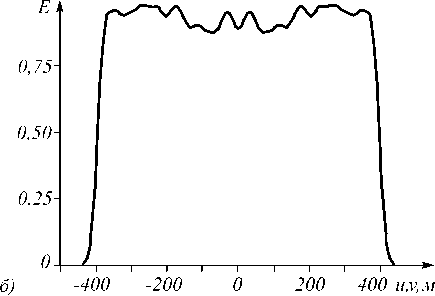
Рис. 6. Полутоновое распределение освещённости, формируемое оптическим элементом с профилем, приведённым на рис. 5 (а); сечение распределения освещённости в плоскости v=0 (б)

Необходимо заметить, что значение световой эффективности 92 % является максимально возможным, так как по 4 % светового потока неизбежно отражается на нижней и верхней преломляющих поверхностях вследствие френелевских потерь.

Для сравнения на рис. 7 изображён профиль оптического элемента, рассчитанного при тех же параметрах, что и оптический элемент на рис. 6, но формирующего заданное распределение освещённости за счёт внешней асферической поверхности. Несмотря на то, что расстояние от источника до внутренней поверхности осталось тем же (3 мм), габаритные размеры оптического элемента существенно увеличились: высота выросла в 2,2 раза, а диаметр – в 1,6 раза.

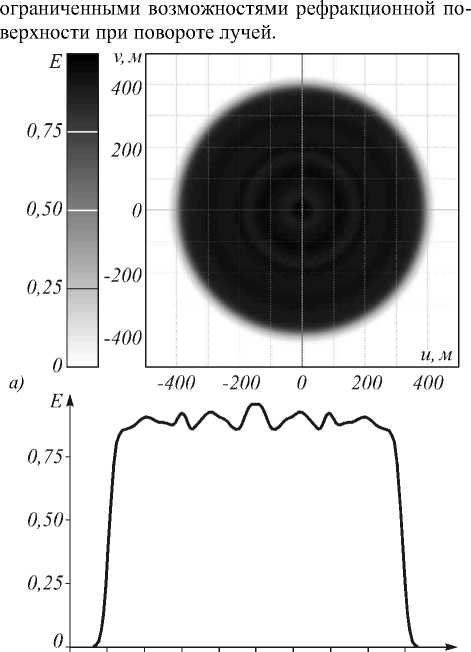
На рис. 8 приведено распределение освещённости, формируемое рассчитанным оптическим элементом в выходной плоскости. Относительное СКО формируемого распределения освещённости состав-

20,44 м.м

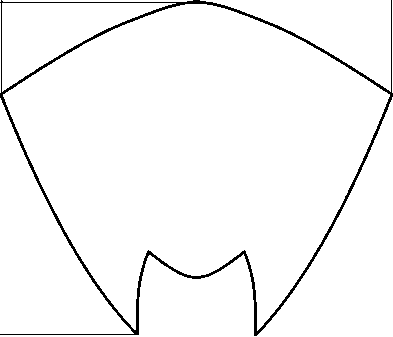
Рис. 7. Профиль оптического элемента с верхней асферической поверхностью, формирующего равномерное распределение освещённости в круге с радиусом 400 мм

Примеры, приведённые на рис. 3–8, подтверждают работоспособность предложенных методов. При угловых размерах освещаемой области, не превышающих 50–60°, использование оптических элементов с TIR–поверхностями позволяет достичь световой эффективности более 90 %. Отметим, что использование оптических элементов, не содержащих поверхностей, работающих по принципу полного внутреннего отражения, в принципе не позволяет эффективно формировать освещённые области с угловыми размерами менее 60–70°. Это связано с

б)      -400   -200     0     200   400 иу,м

Рис. 8. Полутоновое распределение освещённости, формируемое оптическим элементом с профилем, приведённым на рис. 7 (а); сечение распределения освещённости в плоскости v=0 (б)

Вышеприведённые методы расчёта осесимметричных оптических элементов разработаны для случая точечного источника излучения. Оптические элементы на рис. 5 и рис. 7 были промоделированы также и с протяжёнными источниками излучения. Модель протяжённого источника представляла собой круглую площадку, излучающую по закону Ламберта. На рис. 9 приведены зависимости неравномерности формируемого распределения освещённости от радиуса источника излучения. Графики на рис. 9 показывают, что предложенные выше методы обеспечивают хорошую работоспособность в случае, когда диаметр источника меньше расстояния до внутренней поверхности в 5 раз и более – в этом случае СКО формируемого распределения освещённости составляет менее 10%, а эффективность оптических эле- ментов практически не уменьшается. При больших размерах источника на финальном этапе расчёта оптического элемента необходимо использовать оптимизационные методы, учитывающие реальные размеры источника излучения. Тем не менее выражения (1)–(5) могут быть успешно использованы для расчёта начального приближения перед оптимизацией.

Относительное СКО формируемого распределения освещённости, %

О 0,02 0,04 0,08 0,16 0,32 0,64

Отношение диаметра источника к расстоянию до внутренней поверхности

Рис. 9. Зависимости неравномерности формируемого распределения освещённости от относительного диаметра источника излучения для оптических элементов на рис. 5 (сплошная линия) и на рис. 7 (точечная линия)

Заключение

Задача расчёта осесимметричных оптических элементов для светодиодов, содержащих поверхность, работающую по принципу полного внутреннего отражения, сведена к численному интегрированию дифференциальных уравнений первого порядка, разрешённых относительно производных. Рассмотрены две конструкции оптических элементов – с плоской и асферической внешней поверхностью. Показано , что использование оптических элементов, в которых заданное световое распределение формируется за счёт внутренней поверхности, является более целесообразным, так как такие оптические элементы имеют наименьшие габаритные размеры при прочих сходных характеристиках. Исследована зависимость неравномерности формируемого светового распределения от размеров протяжённого источника. Показано, что разработанные методы демонстрируют хорошую работоспособность в случаях, когда размер источника меньше расстояния до внутренней поверхности в 5 раз и более.

Работа выполнена при поддержке Минобрнауки РФ (государственный контракт 07.514.11.4060).