Расчёт оптического элемента для формирования осесимметричного распределения освещённости на поверхности вращения

Светотехнические устройства являются важным элементом большого числа технических систем, включающих дорожное, жилое, промышленное освещение, светотехнические системы транспортных средств и т.д. До недавнего времени основными используемыми источниками света являлись лампы накаливания. В настоящее время эволюция светотехнических устройств направлена на переход от ламп к светодиодам. Использование светодиодов в системах освещения требует применения вторичной оптики, направляющей излучённый светодиодом световой поток в заданную область пространства и обеспечивающей формирование в этой области требуемого распределения освещённости. Расчёт вторичной оптики является сложной задачей и даже в случае точечного источника требует решения нелинейного дифференциального уравнения в частных производных второго порядка [1].

Для получения заданного распределения освещённости в области с малым угловым размером (50–60º и менее) обычно применяют оптические элементы, использующие эффект полного внутреннего отражения (ПВО) для поворота лучей на большие углы. Такие элементы, как правило, имеют две преломляющие поверхности (внутренняя и внешняя поверхности a , d на рис. 1) и одну поверхность, работающую на ПВО (боковая поверхность c на рис. 1). Наличие нескольких рабочих поверхностей в общем случае требует использования сложных оптимизационных и итерационных методов [2–7].

В случае точечного (компактного) источника излучения и осесимметричного распределения освещённости возможно аналитическое решение задачи расчёта оптического элемента. В частности, в работах [8, 9] расчёт осесимметричных оптических элементов светодиодов, содержащих поверхность, работающую по принципу ПВО, сведён к численному интегрированию двух дифференциальных уравнений первого порядка, разрешённых относительно производной. Оптические элементы в [8, 9] предназначены для формирования заданного осесиммет- ричного распределения освещённости в плоскости, перпендикулярной оптической оси.

В данной работе рассмотрена задача расчёта оптического элемента, обеспечивающего формирование заданного распределения освещённости на поверхности, образованной вращением кривой вокруг оптической оси линзы. Указанная задача обобщает результаты работ [8, 9] и включает расчёт оптического элемента для формирования заданного распределения освещённости в плоскости в качестве частного случая. Задача сведена к интегрированию трёх дифференциальных уравнений первого порядка, разрешённых относительно производных. В качестве важного частного случая рассмотрен расчёт оптического элемента для фокусировки в отрезок оптической оси.

• 1.    Расчёт формы профиля линзы

Рассмотрим задачу расчёта оптического элемента для формирования требуемого распределения освещённости на поверхности вращения с образующей ρ = ρ ( z ), z ∈ [ z 1, z 2] (рис. 1). Функцию ρ ( z ) будем считать монотонной (возрастающей или убывающей), чтобы поверхность не содержала областей геометрической тени.

Считаем, что точечный источник находится в начале координат. Для создания требуемого распределения освещённости на поверхности вращения будем использовать осесимметричный преломляющий оптический элемент с профилем, приведённым на рис. 1. Профиль элемента состоит из частей а , b , с и внешней плоской поверхности d (рис. 1). Рабочими поверхностями элемента являются поверхности a и с . При этом поверхность a является преломляющей, а поверхность с работает на эффекте полного внутреннего отражения (ПВО). Поверхность b является сферической с центром в начале координат, поэтому преломления на ней не происходит.

Рассмотрим расчёт части a профиля элемента (рис. 1). Обозначим r a ( β 0) длину радиус-вектора точки профиля, где β 0 ∈ [0, β 0 max] – угловая координата падающего луча (рис. 2).

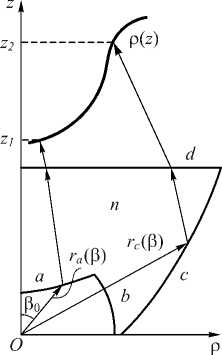
Рис. 1. Профиль ПВО оптики с верхней плоской поверхностью

В работе [8] для г_а ( 3 0) получено следующее дифференциальное уравнение:

d r а ( в о )        .) sin ( в о +в а ( в о ) )

d e „ = a ^{( в} " ' 1/ n - cos ( в о +в а ( в о ) ) '

где функция в a ( в _о) задаёт направление преломлённого луча (рис. 2), n – показатель преломления материала элемента.

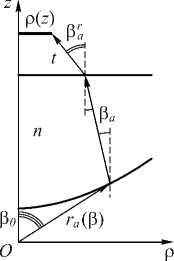
Рис. 2. Преломление луча на поверхности а и на внешней плоской поверхности d

Для расчёта функции в a ( в _о) в (1) используем закон сохранения светового потока. Световой поток, падающий на элемент d S поверхности вращения с образующей p ( z ), должен быть равен соответствующему световому потоку от источника, излучённому в элемент телесного угла d Q ₀ = 2 п sin в _о d в ₀. Таким образом, можно записать следующее равенство:

Отметим, что корректное задание освещённости E ( z ) требует выполнения закона сохранения светового потока:

J I о ( в о ) Sin Р _od Р _o = 0

z ₂

J E ^{( z} ) p^{( z} )

z ₁

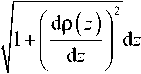
Запишем уравнение выходящего из оптического элемента луча в следующем параметрическом виде:

₌ р ( ^в о ) =p h №) ^- t sin ^в а №) ,                  (5)

_ z № )=h+t cosв а №), где ph (во) - координата точки пересечения луча, преломлённого на части a профиля, с выходной плоскостью z = h, в а (во) — угловая координата луча после преломления на выходной плоскости. Согласно закону Снеллиуса, sin ва (во ) = n • sin ва (во ) .

Из геометрии задачи (рис. 2) несложно получить p h ( в о) в (5) в виде:

p h ( в о ) = p а ( в о ) - ( h - Z a ( в о ) ) tg в а ( в о ) ,         (6)

где p а ( в о) = Г а ( в о) sin в о, Z a ( в о) = Г а ( в о) COS в о — координаты пересечения падающего луча c профилем a . Будем считать, что p ( в _о) в правой части первого уравнения в (5) соответствует радиальной координате образующей поверхности вращения p = p ( z ) при z = z ( в о) , где функция z ( в _о) является решением уравнения (3). Тогда, исключая из первого уравнения в (5) переменную t и подставляя полученное выражение во второе уравнение, получим:

^z ( ^в о ) = ^{h +} [ r h ( ^в о ) ^- p ( ^в о ) ] ^х

• V^{1 -} ( n ^{sin в} а ( ^в о ) ) ^{2                                 (7)}

^Х"--- -о/оч --.

n sin ^в а ( ^в о )

Продифференцируем уравнение (7) по переменной в о и получим следующее уравнение:

^{d в} а ( ^во )     /■ /О 4 ^f 2 ( ^во )

d в    = f ^{( в}о ) } 3( в ;)^{cos в} а ^) •             ⁽⁸⁾

I о ( Р о ) ^{d Q} о = ^{2 n I} о ( Р о ) ^sin 1Ш =

где

= E ( z ) d S = 2 n E ( z ) p ( z )J1 + ( d p ( z ) /d z ) d z ,

f 1 ( ^в о ) = ^{1 - [} n ^{sin в} а ^] 2 ,

где I _о ( в _о) — интенсивность источника излучения, E ( z ), z е [ z i, z ₂] - заданная освещённость на поверхности вращения. Представим уравнение (2) в следующем виде:

f 2 (во ) = Т/ЦвТ)

d r

- sin ( ^в а ^+в о ) ^{+ d в} 0

dz ( Р о ) =          I о ( Р о ) ^{sin в} о

dРо     E (z ) p ( z) 1 + ( dp( z) / dz)

^{+ Г}а cos ( ^в а ^+в о ) - -d ^ cos ^в а ^{d в} 0

f 3 ( ^в о ) = ( ^{z ( в} о ) ^{- h} ) n cos^{3 в} а ^{+ + (} h ^{- Г}а cos ^в а ) ( f 1 ^{( в} о ) ) ^3/2 .

n d z

-       Sin2ва , (9)

2 d в о

Производные ^a , z в (9) определены в ^{d р} о     ^{d р} о

dp   dp dz уравнениях (1), (3), а =       . После выполне-

Фо dz ^{d р} о

ния указанных подстановок правая часть уравнения (9) будет зависеть только от переменной р _о и функций r a ( Р о), z ( Р о). Таким образом, расчёт части a профиля оптического элемента сводится к интегрированию системы трёх дифференциальных уравнений (1), (3), (8), разрешённых относительно производных. При этом уравнение (3) является независимым от уравнений (1), (8) и может быть решено отдельно. Указанная система может быть проинтегри-

рована с использованием стандартных численных методов (например, метода Рунге–Кутты).

Рассмотрим расчёт части с оптического элемента (рис. 1), работающей на ПВО. Обозначим r c ( р _о), Р 0 е [ Р о max, п /2] длину радиус-вектора точки профиля c . В [8, 9] для r c ( Р 0) получено следующее диффе-

ренциальное уравнение:

^d r c ( Р о ) d Р о

- r c

( Р о ) ctg

во + рc (во )

где функция Р _c ( Р _о) задаёт направления луча после ПВО (рис. 1). Для расчёта части с профиля оптического элемента могут быть также записаны дифференциальные уравнения, которые полностью аналогичны уравнениям (3), (8).

Важным частным случаем рассмотренной задачи является расчёт оптического элемента для фокусировки в отрезок оптической оси. В этом случае закон сохранения светового потока (2) принимает вид:

^{2 п /} о ( ^р о ) sin ^p о ^{d p} о = E ( z ) d z ,

d z ( ^р о )     2 п

= ^T^ I о ^{( р} о ) sin ^р о , ^{d р} о      E ( ^z )

где E ( z ) – заданная освещённость на отрезке [ z 1, z 2] оптической оси. При этом функция p ( р _о) = о в уравнениях (7) – (9).

2. Результаты численного моделирования

Разработанный метод расчёта оптических элементов был реализован в среде программирования Matlab [10].

Были рассчитаны оптические элементы для равномерного освещения полусферы и отрезка [ z 1, z 2] на оптической оси. Уравнение образующей полусферы имеет вид:

p ( ^z ) = V ^R ^^- ( z" z о)^? , ^{z е} [ ^z о , ^z о ⁺ R ] , ⁽¹²⁾

где R – радиус полусферы, z 0 – координата центра сферы на оптической оси. Расчёт оптического элемента для освещения полусферы производился при параметрах: R =50 мм, z 0=215 мм. Расчёт оптического элемента для равномерного освещения отрезка оптической оси производился при z 1 =40 мм, z ₂ =90 мм.

б)

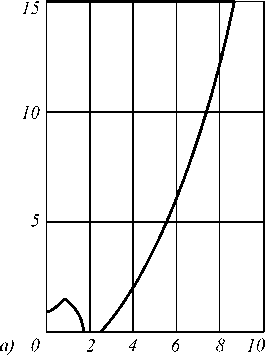
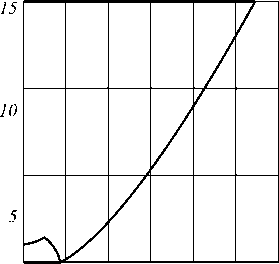
Рис. 3. Профиль линзы, обеспечивающей равномерное освещение полусферы (а); отрезка оптической оси (б)

При расчёте обоих элементов были использованы следующие параметры: толщина элемента h = 15 мм, показатель преломления материала элемента n = 1,41 (соответствует силикону), угловой размер части а профиля а р _отах=3о°. Источник излучения считался ламбертовским, при этом 1 ₀( Р _о) = cos р _о в (3). Рассчитанные профили элементов приведены на рис. 3. Для проверки правильности расчётов было проведено моделирование работы рассчитанных оптических элементов в программе для светотехнических расчётов Zemax с использованием метода трассировки лучей [11]. Распределения освещённости, рассчитанные для 1000000 лучей, приведены на рис. 4, 5. При этом выбор лучей осуществлялся по методу Соболя [12], который позволяет достичь большей точности расчёта.

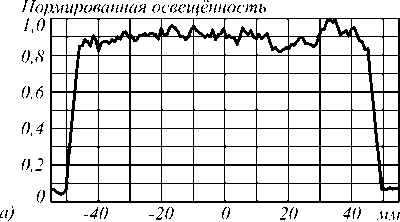
Расчётные распределения освещённости на рис. 4 показывают высокую равномерность распределения освещённости на полусфере. Некоторые осцилляции освещённости вдоль образующей полусферы на рис. 4 а объясняются погрешностью метода трассировки лучей. Среднеквадратичное отклонение освещённости от среднего значения на поверхности полусферы составляет 6,5%. При этом энергетическая эффективность элемента (доля излучённого светового потока, попавшая на поверхность полусферы) превышает 89%.

Расчётные распределения освещённости на рис. 5 показывают формирование области равномерной освещённости вдоль отрезка оптической оси.

б)   -55 -40   -20    0    20    40 55

Рис. 4. Нормированные распределения освещённости, полученные при моделировании в программе Zemax оптического элемента на рис. 3а для равномерного освещения полусферы: освещённость вдоль образующей полусферы (а), полутоновое распределение освещённости на полусфере (б)

О 10

100 б)

-10 0 10

1,0 0,9 0,8 0,7

0,6 0,5

0.4

0,3

0,2 0,1 О

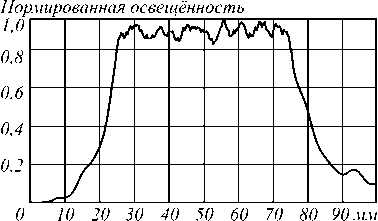
Рис. 5. Нормированные распределения освещённости, полученные при моделировании в программе Zemax оптического элемента на рис. 3б для равномерного освещения отрезка оптической оси: освещённость вдоль оптической оси (а), полутоновое распределение освещённости в плоскости, содержащей оптическую ось (б)

Отметим, что координата z на рис. 5 отсчитывается от выходной плоскости оптического элемента, поэтому отрезок располагается при z ∈ [25, 75] мм. Среднеквадратичное отклонение освещённости от среднего значения в области отрезка составляет 8,3%. Световая эффективность оптического элемента (доля излучённого светового потока, попавшая на плоскость регистрации на рис. 5 б ) также превышает 89%.

При расчётах мы предполагали, что источник является точечным, но в реальных условиях размеры излучающей области светодиодов начинаются от десятых долей миллиметра. Отметим, что предлагаемые в статье элементы чувствительны к размеру источника, особенно это касается линз, которые формируют равномерное освещение отрезка. Так, при использовании источника с прямоугольной областью излучения размерами 0,1 мм ×0,1 мм среднеквадратическое отклонение возрастало с 8,3% до 15%.

Заключение

Задача расчёта преломляющего оптического элемента, предназначенного для формирования заданного осесимметричного распределения освещённости на поверхности вращения, сведена к численному интегрированию трёх дифференциальных уравнений первого порядка, разрешённых относительно производных. Рассчитаны оптические элементы для формирования равномерного распределения освещённости на сферической поверхности и вдоль отрезка оптической оси. Результаты моделирования в программе для светотехнических расчётов Zemax показывают высокую равномерность формируемых распределений освещённости и подтверждают правильность предложенного метода расчёта.

Работа выполнена при поддержке грантов РФФИ 13-07-97001, 12-07-13113 и ФЦП «Кадры» (соглашение 8027).