Расчёт параметров и характеристик вращающегося лунного реактивного пенетратора

Теоретические и экспериментальные исследования по внедрению твёрдых тел в грунты за счёт кинетической энергии, накопленной на вне грунтового участка траектории, показывают, что участок движения в грунте иногда несёт явно выраженный криволинейный характер, при котором возможен значительный уход от прямолинейного движения вплоть до полного разворота проникающего тела и движения его донной частью вперёд. На характер движения существенное влияние оказывают силы, которые в свою очередь зависят как от формы тела, так и от начальных условий внедрения, определяемых наличием угла между вектором скорости и осью симметрии, а также угловыми скоростями прецессии, нутации и собственного вращения.

При внедрении в грунт реактивного пенетратора с работающим двигателем на его устойчивость, кроме указанных выше факторов, влияют и такие, как величина тяги, её эксцентриситет и возможность закрутки.

Целью настоящей работы является определение параметров внутренней баллистики реактивного двигателя твёрдого топлива (РДТТ), установленного на реактивном пенетраторе, входящем в грунт с высокой скоростью вращения вокруг собственной оси.

Для определения величины давления в камере вращающегося двигателя обычно используют известные уравнения баланса прихода и расхода газа, что и в случае невращающегося реактив- ного двигателя твёрдого топлива. Отличие внутренней баллистики вращающегося РДТТ состоит в том, что влияние вращения на рабочий процесс учитывается [1]:

– коэффициентом расхода газов из камеры вращающегося двигателя

1—и

^Arot ^{= A} 0

1 +

I к + 1 кр )

;

– изменением скорости эрозионного горения твёрдого топлива при вращении РДТТ

ε rot = 1 +Bn ^0,5;

– коэффициентом тепловых потерь

χ rot

₂ 0,4

1 - 0,16 ( 1 + tanа_кр )

1 + 2ψ ^,

где А ₀ – коэффициент расхода газов с камеры сгорания невращающегося РДТТ. Величина коэффициента расхода газов определяется по зависимости

A = M <  1, 0 _{M T}

где М ₀ – реальный (опытный) массовый расход, учитывающий все возможные виды потерь,

pкр fкр уменьшающих расход газов через сопло; M =       – теоретический расход газов через со-

χ RT 0

пло; p _кр – давление торможения на входе в сопло; f _кр – площадь критического сечения сопла; X - коэффициент тепловых потерь; RT₀ - приведённая сила твёрдого топлива; B = 3,7 - 10 ^{- 6}

об при n < 103      ; к - показатель адиабаты; а, мин

кр

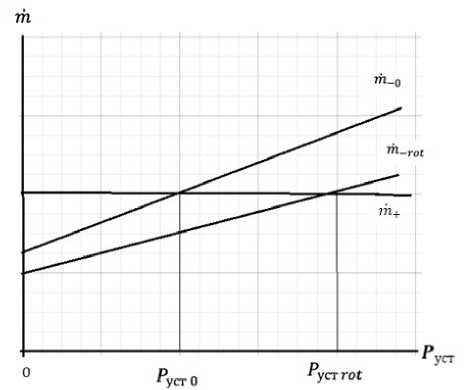
Рис. 1. График, иллюстрирующий принцип стационарности

Fig. 1. Graph illustrating the principle of stationarity

угол закрутки газового потока в критическом сечении сопла двигателя; n – количество оборотов вращающегося грунтового реактивного пенетратора; υ – показатель степени в законе скорости горения топлива; ψ – относительная доля сгоревшего заряда.

Алгоритм определения давления в камере сгорания вращающегося двигателя твёрдого топлива

1. Установившееся давление на участке стационарной работы РДТТ

На рис. 1 графически изображён принцип стационарности работы вращающегося РДТТ.

Здесь тг + - газоприход в камеру сгорания РДТТ; тг _{- 0} и тг - rot - газорасход невра-щающегося и вращающегося двигателя, соответственно.

Из графика видно, что уменьшение газорасхода у вращающегося двигателя приводит к увеличению величины установившегося давления в его камере сгорания, т. е. Р уст _rot >  Р₀.

При этом для расчёта P _{уст rot} используется уравнение

Р .

уст rot

^ 1

V N ,

N где     N1 =   ;

ε

P

е =------------;

Р m X rot RT O

Xrot (“)

из      ( з ) ;      N =

^ 2 A rot p k f ср

5 _г U m р т X rot RT O ’

U m = f . ( T 3 ) f 2 ( Р к ) f 3 ( « кр ) f 4 ( X 0 ) — U m = f . f 2 f 3 f 4 – скорость горения твёрдого топлива, зависящая от температуры заряда ( f ( Т 3 ) ) , давление в камере сгорания f 2 ( p _к ) , степень закрутки f з ( а_кр ) газового потока и критерий Победоносцева f 4 ( х 0 ) [2; 3].

На рис. 2 представлена зависимость величины установившегося давления в камере вращающегося РДТТ от степени закрутки газового потока.

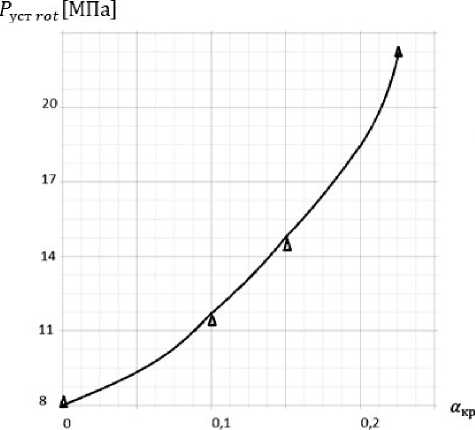
Рис. 2. Зависимость величины установившегося давления в камере сгорания от степени закрутки газового потока

Fig. 2. Dependence of the steady-state pressure in the combustion chamber on the degree of swirl of the gas flow

Расчёты P _{уст rot} проводились для реального двигателя модельного грунтового реактивного аппарата диаметром 40 мм. Здесь ∆ – отмечены опытные значения установившегося давления. Видно хорошее согласование расчётных и опытных данных.

Таким образом, установившееся давление в камере РДТТ реактивного пенетратора изменяется в зависимости от скорости его вращения вокруг собственной оси. При этом с увеличением степени закрутки газового потока величина установившегося давления растёт, темп нарастания давления в процессе выхода двигателя на установившийся режим работы падает и при заданной массе топлива время работы двигателя уменьшается (рис. 3).

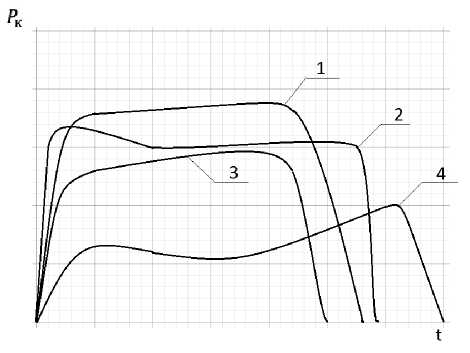
Рис. 3. Типовые зависимости давления в камере сгорания для вращающихся РДТТ:

1 – для вращающегося РДТТ; 2 – для невращающегося РДТТ; 3 – отмечается некоторое

об увеличение установившегося давления в камере для вращающихся двигателей при n < 103    ;

мин

• 4 – показана возможность появления второго максимума, величина которого больше первого

Fig. 3. Typical pressure dependences in the combustion chamber for rotating solid propellant rocket engines:

• 1    – for a rotating solid propellant rocket engine; 2 – for a non-rotating solid fuel jet engine;

• 3    – there is a slight increase in the steady-state pressure in the chamber for rotating engines at n <  10³ rpm/min;

• 4    – shows the possibility of the appearance of a second maximum, the value of which is greater than the first

Следует отметить, что давление в камере сгорания вращающегося двигателя может быть скорректировано либо использованием в его конструкции объёма для дожигания, что увеличивает свободный объём камеры сгорания, либо изменением коэффициентов тепловых и гидравлических потерь. Коэффициент гидравлических потерь может быть рассчитан по формуле

1,375

• 5    = ^ 0 ( 1 + ^tg ^а кр )     ,                                          ⁽⁶⁾

• 2.    Выход вращающегося РДТТ на стационарный режим

где ^ o - коэффициент гидравлических потерь при одномерном течении газа по трубе пРи ^а кр = ⁰ •

Расчёты показывают, что величина а _кр по причине гидравлических потерь до значений а _кр ~ 0,2 почти не изменяется, поэтому учёт её уменьшения следует проводить при а _кр >  0,3 - 0,4, когда а _кр уменьшается на 13-35 %.

При расчёте зависимости давления по времени выхода твердотопливного вращающегося двигателя на стационарный режим работы, как и при расходах РДТТ [3; 4], определяют пара- метр

Ф 2 A rot bf ср У/ rot^RT0 ( 1 ^-и)

Wг где вращение учитывается введением коэффициентов Arot и хrot; b и v - коэффициенты в законе горения топлива; WF = рuSг - газовый приход в камеру сгорания; и - скорость горения топлива; Sг – поверхность горения топливного заряда.

После этого рассчитывается полное время выхода РДТТ на стационарный режим тр = ^. a 1 - p

где p = 0,99 – предельные относительные давления в камере сгорания в процессе выхода РДТТ на установившийся режим работы; p_b – давление в камере при воспламенении заряда.

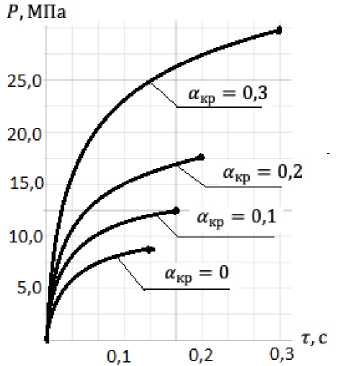
Рис. 4. Зависимость давления в камере сгорания от времени при выходе двигателя на установившийся режим

Fig. 4. Dependence of pressure in the combustion chamber on time when the engine reaches steady state

Расчёты, приводимые для вращающегося грунтового реактивного пенетратора диаметром 240 мм при углах закрутки а _кр = 0,1; 0,2; 0,3 показали, что: 1) время выхода двигателя на установившийся режим работы с увеличением скорости вращения увеличивается на 23 % при а _кр = 0,1, на 46 % при а _кр = 0,2 и на 130 % при а_кр = 0,3, т. е. от 0,13 с до 0,3 с; 2) увеличивается величина установившегося давления по сравнению с невращающимся двигателем.

Для получения зависимости (рис. 4) в начале было определено т _р по формуле (8), а затем было выбрано три значения т 1 , т ₂ , Т 3 , лежащих в интервале между т _р и 0, и по величине этих времен определились относительные давления p ₁ , p ₂ , p ₃ по формуле

Pi = [1 -(1- Рь)

1-и

- а т, e i

1 -и

Затем pi пересчитывались в реальные расчётные давления по зависимости:

Pi = Руст rot Pi , где pi вычисляют до p = 0,99.

• 3.    Расчет давления в период свободного истечения газов из камеры РДТТ

Как и для случая расчета периода последействия для невращающегося двигателя, определяется время конца горения заряда по формуле [3–5]

т к =

e u,

где e – толщина горящего свода, для трубчатого заряда, горящего по наружной ( D ) и внутренней ( d ) поверхностям, в частности, равна

D - d е =-----

.

С учетом зависимости скорости горения заряда от давления в камере сгорания, очевидно, что время конца горения для вращающегося двигателя будет меньше времени конца горения заряда невращающегося двигателя, поскольку давление на установившемся режиме работы вращающегося двигателя больше давление установившегося режима невращающегося двигателя.

Время полного истечения газов из камеры сгорания после сгорания твердого топлива вычисляется по формуле

т

св

В

p krot 1,8

0,1

D K -1 Ф2 Arotf кр b#r^RTo где В =------------; pk =1,8 бар - давление в камере сгорания, до которого

• 2         W км

справедлива формула надкритического истечения.

Зависимость давления по времени свободного истечения газов определяется в следующей последовательности:

• 1)    время т_св развивается на три интервала, где т 1 , т ₂ и Т 3 - меньше т _св ;

• 2)    по формуле p_i =     ^pkrot _{2 k} производится расчет p ₁ , p ₂ и p ₃ .

(1 + B т i ) ^{1 = 1}

Кривая, проходящая через точки расчета, описывает период свободного истечения газов из вращающегося РДТТ.

На рис. 5 показан график зависимости времени свободного истечения из камеры вращающегося двигателя от степени закрутки грунтового реактивного пенетратора диаметром 240 мм.

Было получено при акр > 0, тсв = 0,173 с; при акр = 0,1, акр = 0,2 и акр = 0,3, тсв1 = 0,22 с, тсв2 = 0,32 с и тсв3 = 0,55 с , соответственно.

Из графика (рис. 5) видно, что с увеличением параметров закрутки, а, следовательно, и числа оборотов реактивного пенетратора, время свободного истечения газов из камеры сгорания после окончания горение топлива увеличивается.

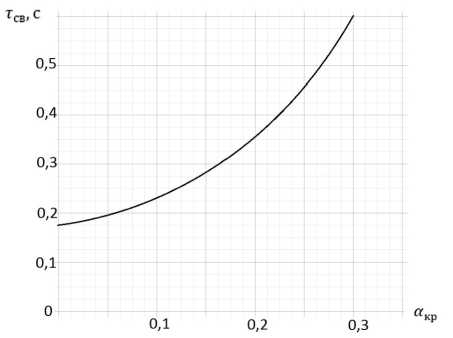
Рис. 5. Расчётная зависимость времени истечения от угла закрутки газового потока РДТТ

Выбор линейных и угловых размеров сопла вращающегося двигателя

Выбор размеров одинарного сопла или сопел соплового блока вращающегося РДТТ проводится по тем же зависимостям, что и для превращающегося двигателя, но с учетом установленных ранее зависимостей и коэффициентов.

Используя зависимости (5) для расчетов установившегося давления в камере вращающегося двигателя, можно найти площадь критического сечения сопла двигателя по формуле [1]

Fig. 5. Calculated dependence of the exhaust time on the swirl angle of the gas flow of a solid fuel jet engine

S r U т Р тУ X rot RT 0

Ф 2 A rot bp rov

dкр= 4fкр , (15) πn где n - число сопел; Arot (акр ), Xrot (акр ) - коэффициенты; prot - проектное давление у стенки камеры двигателя.

Проведенный сравнительный анализ расчетов сверхзвуковой части сопла вращающегося и невращающегося двигателей показал, что оптимальный угол сверхзвуковой части вращающегося двигателя соответствует оптимальному углу сопла невращающегося РДТТ и равен 20°. Опытные данные, представленные в работе [1], подтверждают сделанный вывод, а также показывают, что угол входа в сопло при наличии вращения потока следует выбирать большим, чем для сопла при течении одномерного потока.

На рис. 6 приведена опытная зависимость единичного импульса J ед от половины угла входа в сопло α. Из графика видно, что J ед достигает максимума при 2α = 180°, т. е. при плоской стенке соплового блока. Этот эффект объясняется тем, что плоская стенка полностью гасит осевую составляющую скорости газового потока и увеличивает ее радиальную составляющую, увеличивающую расход газа через сопло.

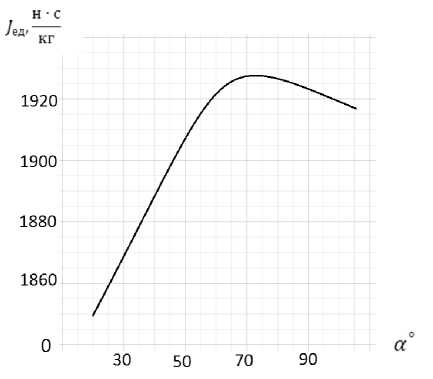
Рис. 6. Зависимость величины единичного импульса от половины угла входа в сопло двигателя

Fig. 6. Dependence of the magnitude of a single impulse on half the angle of entry into the engine nozzle

Для одинарного сопла формула силы тяги сможет быть записана следующим образом

P rot = K д P rot f k р ^ф 1 ^ф 2 A rot , ⁽¹⁶⁾

где K _д - коэффициент тяги; f _ср - площадь критического сечения сопла; ф 1 = 0,95-0,98 -коэффициент скорости; ф ₂ - коэффициент расхода сопла при течении газа без закрутки; Arot = f ( а _кр ) - коэффициент расхода при вращающемся истечении газа.

Таким образом, зная законы изменения давления в камере сгорания вращающегося РДТТ и используя приведенные формулы для силы тяги, можно графически построить зависимости P_rot ( т ) для любого типа вращающегося двигателя [6-8].

Анализ зависимостей для силы тяги вращающихся грунтовых реактивных аппаратов позволяет утверждать, что величина силы тяги у таких двигателей будет меньше, чем у невращаю-щихся при прочих равных условиях.

Разница в силах тяги будет определяться отношением тогда

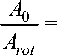
(р rotкр

Р,.

к   ^0к Р У

P 0

Prot

1- v

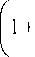
к 2 ^ 1- v α²

к - 1 кр У

k

^{1 +} к 1 ^а к ^р

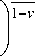
Для реальных твердых топлив и = 0,5-0,67 при акр = 0,1-0,15 значение отношений тяги P приходится в пределах 0 = 1,1–1,36, т. е. тяга невращающегося двигателя на 10–36 % боль-Prot ше, чем тяга у вращающегося двигателя [9–11].

Экспериментальные исследования вращающихся ракетных двигателей твердого топлива, снаряженных многошашечными зарядами твердого топлива, показали, что в отличие от РДТТ с одношашечным зарядом неравномерность давления в камере сгорания наблюдается только в предсопловом объеме. При этом чем больше шашек в заряде, тем меньше степень закрутки как в канале отдельной шашки, так и в предсопловом блоке в целом [12–15].

Заключение

В рамках проведенного исследования решены следующие задачи:

• 1.    Установлено, что на параметры внутренней баллистики вращающихся РДТТ основное влияние оказывают коэффициент расхода газов из камеры вращающегося двигателя, эффект эрозионного горения твердого топлива и изменение коэффициента тепловых потерь.

• 2.    Приведены основные расчетные зависимости для определения давления в камере сгорания вращающегося двигателя твердого топлива для периодов выхода давления на стационарный режим работы двигателя, работа двигателя на стационарном режиме и в период свободного истечение газов из камеры РДТТ.

• 3.    Представлена методика выбора линейных и угловых размеров сопла вращающегося двигателя, позволившая провести сравнительный анализ расчетов сверхзвуковой части вращающегося и невращающегося двигателей.

• 4.    Приведена оценка силы тяги для одинарного сопла вращающегося РДТТ. Установлено, что величина силы тяги вращающихся двигателей (при прочих одинаковых условиях в камере сгорания) в 1,1–1,36 раза меньше, чем у невращающихся РДТТ.

• 5.    Проведённые опыты показали уменьшение степени закрутки газового потока вращающихся двигателей твердого топлива при увеличении количества топливных шашек в заряде двигателя.