Расчёт параметров и компьютерное моделирование синусных фильтров в частотно-регулируемом электроприводе
Автор: Пустоветов Михаил Юрьевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 3 (64) т.12, 2012 года.
Бесплатный доступ
Рассмотрены вопросы расчёта параметров синусных фильтров для частотно-регулируемого электропривода. Приведены результаты компьютерного моделирования функционирования синусных фильтров.
Синусный фильтр, асинхронный двигатель, широтно-импульсная модуляция, преобразователь частоты, озонирование изоляции
Короткий адрес: https://sciup.org/14249841
IDR: 14249841 | УДК: 62-83
Текст научной статьи Расчёт параметров и компьютерное моделирование синусных фильтров в частотно-регулируемом электроприводе
Введение. В настоящее время высокая эффективность использования частотного регулирования скорости вращения в электроприводе переменного тока, особенно для вентиляторов и насосов, ни у кого уже не вызывает сомнения. Однако настал тот момент, когда российских пользователей приводов с частотным регулированием начали настигать некоторые негативные побочные следствия этой современной технологии. Речь идёт об эффекте озонирования изоляции, выражающемся для стороннего наблюдателя в резком запахе озона вблизи работающего двигателя, питаемого от преобразователя частоты (ПЧ). Запах озона является лишь самым явным, но промежуточным и не самым неприятным проявлением процесса ускоренной деградации изоляции электрической машины. Одним из эффективных способов предотвращения негативного воздействия высокочастотных импульсов напряжения ПЧ на изоляцию двигателя является установка между ним и ПЧ синусного фильтра (СФ).
Первопричина данной проблемы кроется в несинусоидальной импульсной форме питающего напряжения с очень крутыми фронтами, подаваемого от ПЧ на двигатель. Допустимое ограничение составляет 500 В/мкс [1], но реальные значения по ряду причин могут превышать его. Проблему может усугублять эффект длинного кабеля, когда ввиду несогласованности волновых сопротивлений ПЧ, кабеля и электрической машины между ПЧ и двигателем возникают эффекты отражения волн напряжения, способные приводить к высокочастотным перенапряжениям, в 2-3 раза превышающим амплитуду импульсов, формируемых на выходе ПЧ [2]. Эти условия способствуют возникновению явления коронного разряда, выражающегося в виде частичного разряда энергии вдоль небольших пустот, имеющихся в любой системе изоляции. В результате следует постепенная химическая и механическая деградация изоляции [3]. Часто в результате частичного разряда образуется озон, который легко участвует в химической реакции с органическими материалами изоляции, приводящей к разрушению этих материалов. Механическая деградация изоляции является следствием воздействия возникающих при коронном разряде заряженных частиц [3]. Результатом длительного воздействия совокупности описанных явлений будет авария на двигателе.
Известно, что в среднем стоимость ремонта электрической машины составляет треть от стоимости покупки новой. Но приемлемо ли досрочно и внепланово выводить в ремонт двигатель водяной насосной станции (ВНС) городского водоканала с мощностью 250-800 кВт, а то и более? Среди схем частотного регулирования мощных двигателей насосов получила распространение двухтрансформаторная, когда напряжение питающей линии 6 кВ понижается до 0,4 кВ, подаётся на ПЧ, а поступающее с выхода ПЧ напряжение регулируемой величины и частоты (до 0,4 кВ, 50 Гц) повышается снова до 6 кВ и подаётся на двигатель. В этом случае негативное воздействие испытывает также повышающий трансформатор (Т).
Возможны различные решения проблемы. Например, можно с ПЧ использовать электротехническое оборудование, специально для этого разработанное. Но двигатели, предназначенные для питания от ПЧ, дороже своих аналогов для питания от сети промышленной частоты с синусоидальной формой напряжения [2], фактически установленных на ВМС.
Другим решением является синусный фильтр.
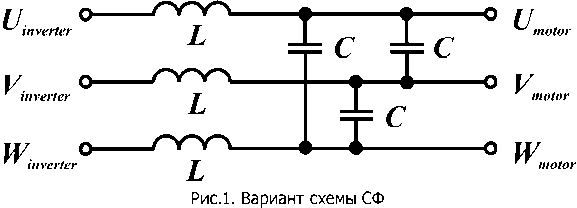
Задача синусного фильтра - сглаживание широтно-импульсно модулированного выходного напряжения ПЧ до практически синусоидальной формы, что создаёт наиболее благоприятные условия работы для двигателей и трансформаторов. СФ является реактивным фильтром нижних частот, который состоит из трёх фазных реакторов и трёх конденсаторов, включённых каждый либо между двумя фазами, как показано на рис.1 (схема «треугольник»), либо между фазой и нейтральной точкой (схема «звезда»). Напряжения с частотами ниже резонансной частоты / пропускаются этим фильтром почти без уменьшения амплитуд. Напряжения с частотами выше / > /р затухают пропорционально 1//2 [4]. Обычно эти фильтры рассчитываются таким образом: резонансная частота / должна быть гораздо выше частоты основной гармоники напряжения, формируемой автономным инвертором напряжения (АМН) в составе ПЧ для питания двигателя, с другой стороны, / должна быть гораздо ниже частоты переключений инвертора или несущей частоты широтно-импульсной модуляции (ШИМ) /щим- При расчёте параметров задаваться можно либо индуктивностью, либо ёмкостью.
Во избежание излишнего падения напряжения на индуктивности в продольной ветви фильтра приходится увеличивать ёмкость в поперечной ветви. СФ в основном воздействует на линейные напряжения. Напряжения нулевой последовательности, неизбежно формируемые АМН, практически не подавляются посредством СФ. Напряжения нулевой последовательности являются источником электромагнитных помех, ёмкостных токов утечки [4, 5] и причиной электрокоррозии подшипников двигателя от подшипниковых токов, приводящей к их интенсивному износу. Таков ещё один побочный отрицательный эффект при питании неспециализированного двигателя от ПЧ [4, 5]. Так как практически вся мощность искажений, формируемая высшими гармониками, протекает через СФ, эти устройства обычно имеют значительные габариты и стоимость.
Расчёт синусного фильтра от индуктивности. Альтернативой покупке дорогого импортного СФ, стоимость которого обычно сопоставима со стоимостью ПЧ, является самостоятельный расчёт и конструирование из доступных отечественных компонентов. Некоторые сведения о расчёте СФ даны в [6, 7]. Зачастую, как в случае трёх ВМС Ростовского водоканала, для которых была выполнена работа по расчёту параметров и моделированию на компьютере СФ, в схемах уже имеется установленный после ПЧ токоограничивающий реактор. Остаётся подобрать конденсаторы. В любом случае для СФ необходимо придерживаться небольшой величины активного сопротивления ветвей с ёмкостями (не более 0,01...0,1 Ом). Для надёжного выполнения функции сглаживания напряжения рекомендуется резонансная частота СФ
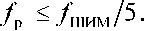
Должно, по меньшей мере, соблюдаться правило: /щим > 2/р. Желательно, чтобы падение напряжения основной частоты на продольной ветви, содержащей индуктивность, последовательно соединённую с активным сопротивлением реактора СФ, не превышало 5 % от значения номинального напряжения. При этом отметим, что параметры некоторых СФ зарубежного производст- ва таковы, что расчётное падение напряжения на продольной ветви достигает на основной частоте 12,2 % и даже 13,8 %. По fp и L, т.е. индуктивности СФ, рассчитывается ёмкость фильтра:
/ х 2
где значение С берётся для случая соединения конденсаторов по схеме «звезда».
Для случая соединения конденсаторов по схеме «треугольник», когда каждый конденсатор подключён к линейному напряжению, ёмкости будут в три раза меньше. Естественно, чем больше /щим'тем меньшая ёмкость фильтра потребуется.
Расчёт синусного фильтра от ёмкости. Сначала выбирается конденсатор из условия компенсации всей реактивной мощности нагрузки на основной частоте ^ = 5ОГц.
Для случая соединения конденсаторов по схеме «звезда» ёмкость Г-образного синусного фильтра С, Ф:
aS 1 R / \ 2
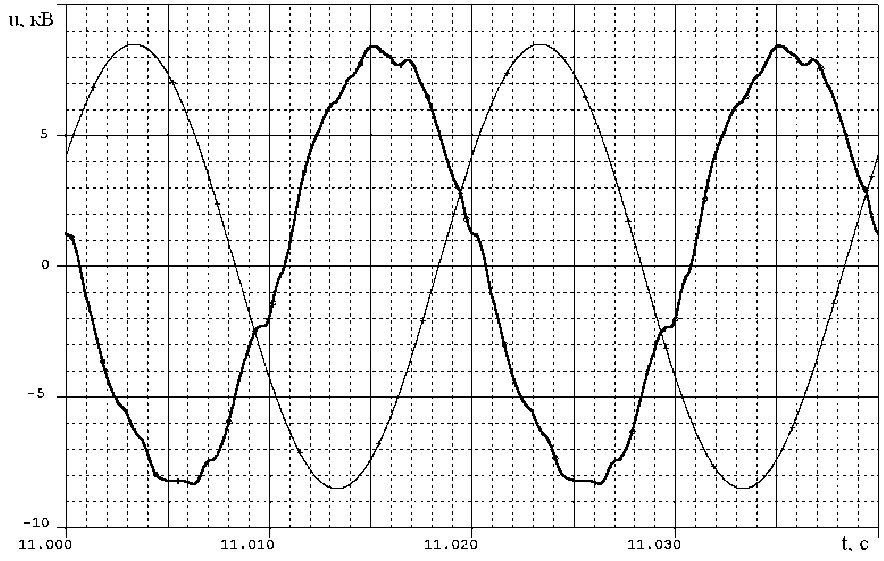
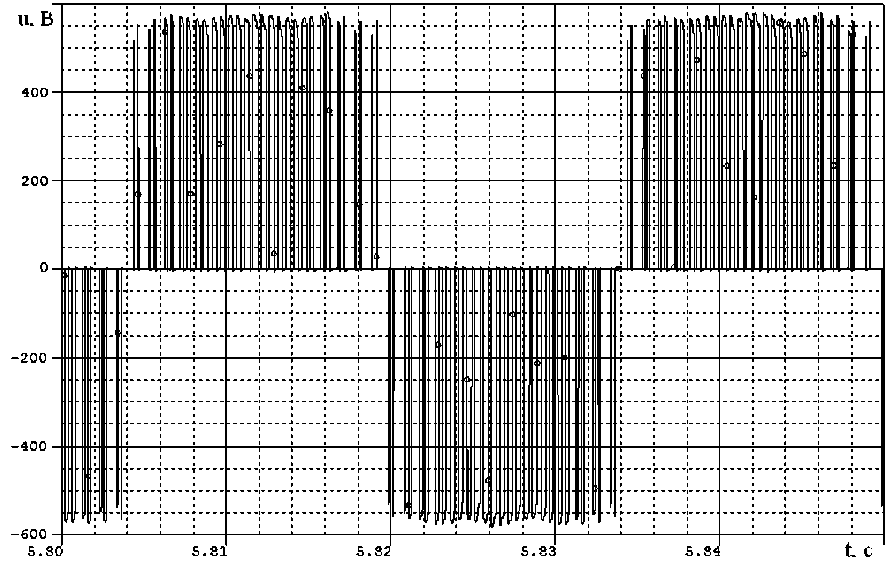
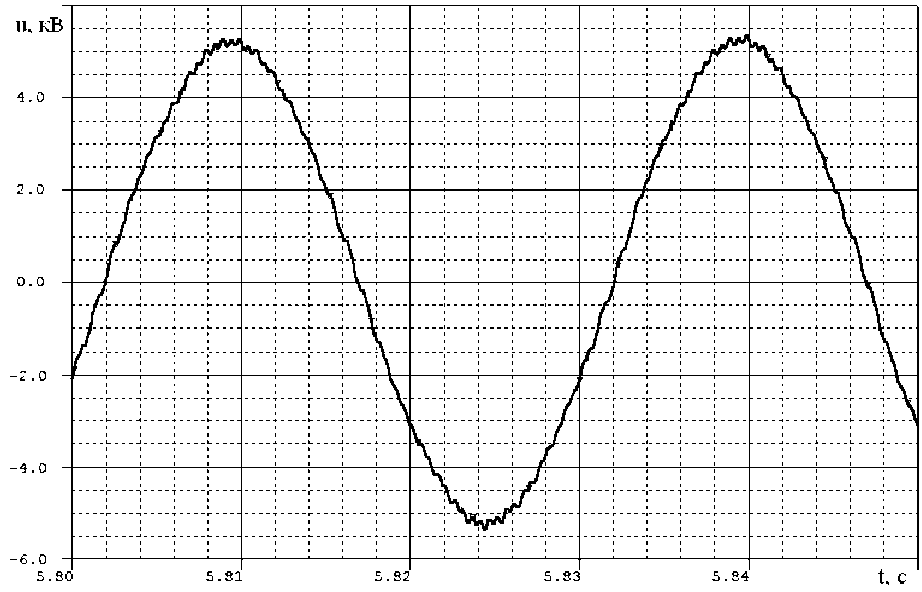
---7V1-(C 3 W\ где S - суммарная мощность нагрузки, подключённой после СФ, BA; cosф - коэффициент мощности нагрузки, о.е.; Ux - действующее значение первой гармоники напряжения на ёмкости Г-образного синусного фильтра, В. По /, выбираемой из условия (1), и С, которая здесь берётся для случая соединения конденсаторов по схеме «звезда», рассчитывается индуктивность фильтра: / х 2 Описание компьютерной модели. Компьютерная модель электропривода водяного насоса, использованная в описываемой работе для моделирования электромеханических и электромагнитных процессов, разработана в среде САПР OrCAD 9.2 и состоит из следующих модулей: трёхфазного источника напряжения (сети 50 Гц, 6 кВ); трёхфазного мостового выпрямителя (В); трёхфазного асинхронного двигателя (АД); трёхфазного трансформатора (Т); двухуровневого автономного инвертора напряжения (АИН), включая системы задания переменной частоты и амплитуды напряжения на его выходе; СФ; насоса (К) [8-15]. Модель по направлению от источника напряжения к нагрузке состоит из следующих элементов: источник трёхфазного переменного напряжения (имитирует сеть 50 Гц, 6 кВ) - понижающий Т - ПЧ в составе В и АИН - СФ - повышающий Т - АД - Н. Напряжение Ud в звене постоянного напряжения ПЧ рассчитано по формуле (5), которая верна как при соединении обмотки НН в «треугольник», так и в «звезду» где Г72лННптр - линейное напряжение обмотки НН понижающего Т. Параметры Г-образного фильтра, т.е. индуктивность Ld в последовательной и ёмкость Cd в параллельной ветвях звена постоянного напряжения ПЧ не заданы. Они рассчитаны из соотношений (6) и (7): 2 • J 1 фПЧ d й f (ЛОТТ ' о/шим d где /фпч - ток фазы ПЧ; /ШИХ1 - частота коммутации ПЧ; L где /ртреб - требуемая резонансная частота фильтра, частота среза. Гармоники напряжения с частотами выше частоты среза нежелательны и не должны быть пропущены фильтром на вход АИН. Для привода АД мощностью 800 кВт данные для расчётов по (6) и (7) и их результаты сведены в таблицу. Принято, что в ПЧ используется В, выполненный по трёхфазной мостовой схеме. Данные к расчётам Cd и Ld и их результаты для привода АД мощностью 800 кВт ^2лННптр ' В ud, в 7фпч' А /шИМ' Гц ^этреб * ГЦ cd, мкФ мГн 400 540 1600 1000 200 3000 0,85 Известно, что при классическом алгоритме трёхфазной синусоидально-треугольной ШИМ, базирующемся на сравнении синусоидального модулирующего сигнала и треугольного сигнала несущей частоты, невозможно получить выходное напряжение первой гармоники АИН даже на уровне 90 % напряжения сети [16]. Нам же необходимо получить при 50 Гц на выходе АИН то же линейное напряжение 400 В, что и на входе выпрямителя. Отсюда вытекает необходимость использования предмодуляции - несинусоидального закона для модуляции длительности импульсов потенциалов фаз фд ф8 и фс. Он обеспечивает увеличение амплитуды основной гармоники, но при этом в спектре ШИМ последовательностей фд ф8 и фс помимо основной содержатся только гармоники нулевой последовательности, т.е. с нечётными порядковыми номерами, кратными трём. Так обеспечивается отсутствие в низкочастотной части спектра фазных и линейных напряжений инвертора гармоник искажения. Дополнительно для повышения выходного напряжения АИН можно использовать перемодуляцию. Под перемодуляцией в данном случае подразумевается увеличение вектора модулирующего (и выходного) напряжения за пределы реализуемых значений, т.е. получение векторов напряжения, больших единицы в относительных величинах. Для моделирования выбран алгоритм синусоидально-треугольной ШИМ с пред модуляцией синфазной с первой третьей гармоникой с амплитудой 0,167 от первой гармоники и перемодуляцией первой гармоники в тг/2 раз [17]. Так как нагрузкой АД являются К, то скалярное регулирование ПЧ происходит по основному закону частотного регулирования Костенко в варианте U//2 = const . Точные характеристики К не заданы, поэтому принимается, что АД работает в номинальном режиме при частоте питающего напряжения 50 Гц. Для упрощения задачи моделирования и за отсутствием точных данных о кривых намагничивания Т и АД, коэффициенты насыщения их магнитных цепей приняты постоянными [18, 19]. Рабочий цикл привода при моделировании задан как частотный разгон за 10 с, работа на частоте 50 Гц в течение 1,5 с, затем частотное торможение в том же темпе, что и разгон. Для определения параметров Т-образной схемы замещения АД использован метод, описанный в работе [20]. Результаты расчётов и моделирования. Расчёты велись для /д™ = 1000Гц, что обусловлено большой протяжённостью соединительных кабелей между ПЧ и АД. Моделирование проводилось для четырёхполюсных АД мощностью 250, 630 и 800 кВт на номинальное линейное напряжение 6 кВ. Результаты моделирования для случая расчёта параметров СФ от индуктивности представлены на рис.2-5, где использован СФ с параметрами: продольная ветвь /, = 0,025 мГн, rL =0,014; поперечная ветвь С = 8360 мкФ, г = 0,01 Ом. Конденсаторы соединены по схеме «треугольник». Заземление нейтрали СФ при соединении конденсаторов по схеме «звезда» никак не влияет на качество работы СФ, что справедливо при любом сочетании заземлённой нейтрали СФ и заземлении нейтралей трансформаторов. Результаты для аналогичных СФ с соединением конденсаторов по схемам «звезда» и «треугольник» не различаются. Ток через конденсатор при- близительно в V3 раз больше при соединении конденсаторов в «звезду» по сравнению со схемой «треугольник». Вариация параметров реактивных элементов СФ до 30% незначительно сказыва- Рис.2. Линейное напряжение на выходе АИН при частоте 50 Гц (АД мощностью 630 кВт) Рис.З. Линейное напряжение сети 6 кВ (идеальная тонкая синусоида) и линейное напряжение на АД (неидеальная жирная синусоида) при частоте 50 Гц (АД мощностью 630 кВт) Рис.4. Линейное напряжение на выходе АИН при частоте 33,3 Гц (АД мощностью 630 кВт) Рис.5. Линейное напряжение на АД мощностью 630 кВт при частоте 33,3 Гц Заключение. Синусный фильтр с выбранными по изложенной методике параметрами демонстрирует удовлетворительное качество сглаживания формы выходного напряжения ПЧ для всех значений его основной частоты. Параметры СФ, рассчитанных от индуктивности, предпочтительнее для выбранной /шим = ЮООГц, так как обеспечивают меньшее падение напряжения основной частоты на индуктивности СФ, меньшее содержание 5-й и 7-й гармоник в спектре напряжения при основной частоте 50 Гц. При /шим > 1250Гц использование метода расчёта параметров СФ от ёмкости даёт значение индуктивности, обеспечивающее падение напряжения основной частоты на продольной ветви СФ менее 10%. Целесообразность использования этого метода расчёта по критерию минимизации падения напряжения основной частоты на продольной ветви СФ возрастает с увеличением несущей частоты ШИМ.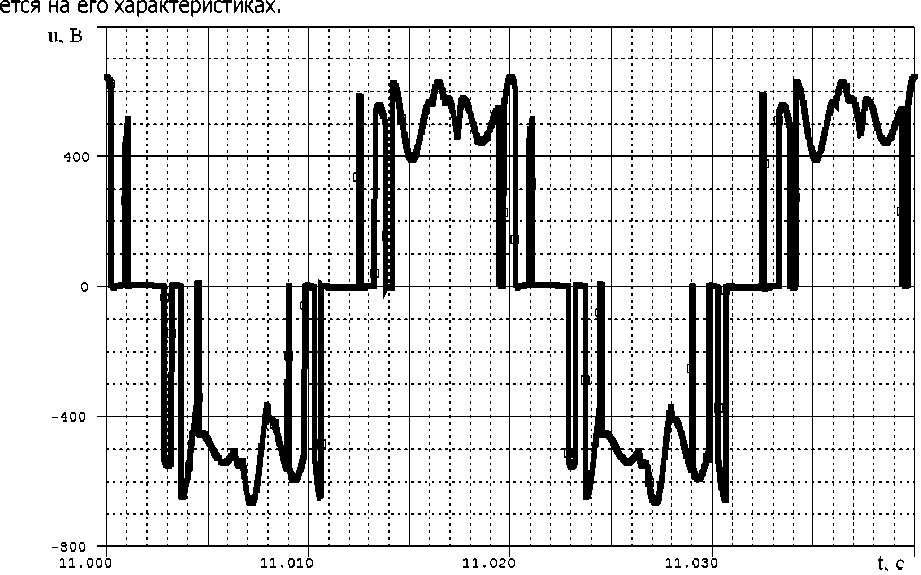
Список литературы Расчёт параметров и компьютерное моделирование синусных фильтров в частотно-регулируемом электроприводе
- ГОСТ Р 51330.8-99. Электрооборудование взрывозащищенное. Часть 7. Защита вида e. (принят и введен в действие Постановлением Госстандарта РФ от 16.12.1999 № 525-ст) -М.: ИПК Издательство стандартов, 2000.
- Пехотский И.В. Моделирование электромагнитных процессов в частотно-регулируемом асинхронном приводе с длинным питающим кабелем/И.В. Пехотский, М.Ю. Пустоветов, П.Г. Колпахчьян, С.Ю. Пустоветова//Электровозостроение: сб. науч. тр. -2003. -Т.45. -С. 257-268.
- Evaluating Inverter-Duty Motor Insulation Systems Using Corona Inception Voltage. The Lincoln Electric Company. Technical Brief. [Электрон. ресурс]. Режим доступа: http://shared.a2zinventory.com/mfg/LincolnMotors/Library/tb-100.pdf (дата обращения: 05.01.12).
- Muetze A. Bearing Currents in Inverter-Fed AC-Motors. Elektrotechnik und Informationstechnik der Technischen Universitaet Darmstadt zur Erlangung des akademischen Grades einer Doktor-Ingenieurin (Dr.-Ing.) genehmigte Dissertation. Darmstaedter Dissertation. 2004. 252 p. [Электрон. ресурс]. Режим доступа: http://www.ew.tu-darmstadt.de/media/ew/dissertationen/dissannette.pdf (дата обращения: 05.01.12).
- Luszcz J., Dworakowski P. Destructive consequences of PWM inverter feeding for traction AC motors. (Chapter 11 in a book: Modern Electric Traction. Edited by K. Karwowski, A. Szelag. 2009 Gdansk University of Technology, Faculty of Electrical and Control Engineering).
- Пустоветов М.Ю. Расчёт и моделирование фильтров du/dt и синус-фильтров для асинхронного электропривода/М.Ю. Пустоветов, И. В. Синявский, С. Ю. Пустоветова//Новые технологии, конструкции и процессы производства: сб. науч. тр./ГОУ Рост. гос. акад. с.-х. машиностроения. -Ростов н/Д, 2008. -С.100-103.
- Пустоветов М.Ю. Расчёт параметров синус-фильтра при несущих частотах ШИМ 900-1000 Гц/М.Ю. Пустоветов, И.В. Синявский//Новые технологии, конструкции и процессы производства: сб. науч. тр./ГОУ Рост. Гос. Акад. С.-х. машиностроения. -Ростов н/Д, 2009. -С.134.
- Пустоветов М.Ю. Модель асинхронного электропривода, выполненная в системе OrCAD 9.2/М.Ю. Пустоветов, И.В. Пехотский, П.Г. Колпахчьян, С.Ю. Пустоветова//Оптимизация режимов работы систем электроприводов: межвуз. сб. науч. тр./КГТУ. -Красноярск, 2002. -С.42-51.
- Пустоветов М.Ю. Учёт потерь в стали посредством схемотехнической компьютерной модели трёхфазного асинхронного двигателя//Новые технологии, конструкции и процессы производства: сб. науч. тр./Рост. гос. акад. с.-х. машиностроения. -Ростов н/Д, 2007. -С.129-132.
- Пустоветов М.Ю. Расчёт активного сопротивления в контуре намагничивания модели асинхронного двигателя, основанной на Т-образной схеме замещения, для случая параллельного соединения активного сопротивления и индуктивности/М.Ю. Пустоветов, И.В. Синявский//Труды Всерос. науч.-практ. конф. «Транспорт -2010», апрель 2010 г.: в 3-х ч. Ч.2. Естественные и технические науки -Ростов н/Д: РГУПС, 2010. -С. 377-378.
- Пустоветов М.Ю. Имитационные модели трехфазного трансформатора/М.Ю. Пустоветов//Математическое и программное обеспечение систем в промышленной и социальной сферах: сб. междунар. тр. -Магнитогорск: ФГБОУ ВПО «МГТУ», 2011. -Ч.2. -С.125-131.
- Пехотский И.В. Моделирование электромагнитных процессов в трансформаторах/И.В. Пехотский, М.Ю. Пустоветов, С.Ю. Пустоветова//Вестник ВЭлНИИ: сб. науч. тр./ОАО «Всерос. науч. ин-т и проектно-конструкт. ин-т электровозостроения» (ОАО «ВЭлНИИ»).-Новочеркасск. -2004. -№2. -С.78-85.
- Пустоветов М.Ю. Имитационное моделирование частотного пуска и торможения асинхронного электропривода с разомкнутой системой управления/М.Ю. Пустоветов, И.В. Синявский, А.В. Чубукин//Тр. Всерос. науч.-практ. конф. «Транспорт-2009». Ч.3/РГУПС. -Ростов н/Д, 2009. -С.371-373.
- Пустоветов М.Ю. Расчёт параметров и компьютерное моделирование синусных фильтров, предназначенных для исключения эффекта озонирования изоляции электродвигателей в частотно-регулируемом электроприводе водяных насосных станций/М.Ю. Пустоветов//Мат. междунар. науч.-практ. конф. «Проблемы трансферта современных технологий в экономику Забайкалья и железнодорожный транспорт». -Чита: ЗабИЖТ, 2011. -Т.1. -С.86-95.
- Пустоветов М.Ю. Моделирование нагрузки на валу и расчёт КПД электрической машины в среде OrCAD 9.2/М.Ю. Пустоветов, С.Ю. Пустоветова//Новая техника и технология в производстве сельскохозяйственных машин: сб. науч. тр./Рост. гос. акад. с.-х. машиностроения. -Ростов н/Д, 2002. -С.145-151.
- Аксёнов М.И. Математическое моделирование электропривода: учеб. пособие/М.И. Аксёнов. -М: Издательство МГОУ, 2005. -185 с.
- Курочка А.А. Выбор алгоритма широтно-импульсной модуляции в автономном инверторе напряжения промышленного электровоза НПМ2/А.А. Курочка, Д.А. Кабанов, Л.Д. Лушникова//Вестник ВЭлНИИ: сб. науч. тр./ОАО «Всерос. науч. ин-т и проектно-конструкт. ин-т электровозостроения» (ОАО «ВЭлНИИ»). -Новочеркасск, 2004. -№1. -С.156-163.
- Пустоветов М.Ю. Способ учёта нелинейности кривой намагничивания при переменной частоте питающего напряжения/М.Ю. Пустоветов, И.В. Пехотский//Вестник ВЭлНИИ: сб. науч. тр./ОАО «Всерос. науч. ин-т и проектно-конструкт. ин-т электровозостроения» (ОАО «ВЭлНИИ»). -Новочеркасск, 2004. -№1. -С.239-249.
- Пустоветов М.Ю. Особенности компьютерного моделирования трёхфазных асинхронных двигателей и трансформаторов с учётом насыщения магнитной цепи по пути основного магнитного потока/М.Ю. Пустоветов, И.В. Синявский//Труды Всерос. науч.-практ. конф. «Транспорт-2011». Ч.1. Естественные и технические науки/РГУПС. -Ростов н/Д, 2011. -С.380-382.
- Пустоветов М.Ю. Приближённый расчёт параметров схемы замещения асинхронного двигателя/М.Ю. Пустоветов, С.Ю. Пустоветова//МГОУ-XXI-Новые технологии. -2004. -№1. -С.25-28.


