Расчёт помех в цепях бортовой аппаратуры космических аппаратов, вызванных электростатическими разрядами

Костин Алексей Владимирович; Пиганов Михаил Николаевич; Kostin Aleksey; Piganov Mikhail

Расчёт помех в цепях бортовой аппаратуры космических аппаратов, вызванных электростатическими разрядами

Автор: Костин Алексей Владимирович, Пиганов Михаил Николаевич

Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc

Рубрика: Технологии в авиационном и ракетно-космическом комплексе

Статья в выпуске: 4-5 т.14, 2012 года.

Бесплатный доступ

В статье приводится способ расчёта помех в цепях бортовой аппаратуры космических аппаратов, вызванных электростатическими разрядами. Приводится пример расчёта. Обсуждаются результаты.

Электростатический разряд, поле, бортовая аппаратура, космический аппарат, излучатель, экран

Короткий адрес: https://sciup.org/148201402

IDR: 148201402 | УДК: 629.78:621.311

Calculation of noise in chains of spacecrafts onboard equipment caused by electrostatic discharges

In article the way of calculation the noise in chains of spacecrafts onboard equipment caused by electrostatic discharges is given. The calculation example is given. Results are discussed.

Текст научной статьи Расчёт помех в цепях бортовой аппаратуры космических аппаратов, вызванных электростатическими разрядами

и было экспериментально показано, что на КА действительно возникают электростатические заряды с разностью потенциалов до 20 кВ. Из анализа имеющихся в литературе данных следует, что космические аппараты заряжаются статическим электричеством практически на всей траектории полета.

Для защиты бортовой аппаратуры (БА) КА применяется ряд мер. Но вопрос о необходимости и достаточности принятых мер по защите от электростатических разрядов (ЭСР) остаётся открытым на этапе проектирования БА, и подтвердить правильность выбранных конструктивных решений можно только при натурных испытаниях системы. Если на этом этапе будет получен отрицательный результат, то возникнет необходимость доработки БА. Такие доработки вызывают дополнительные затраты и могут даже задержать сдачу изделия. Другое дело, если меры, принятые для защиты от ЭСР, избыточные. Это ведёт к удорожанию приборов, увеличению их массы и габаритов.

В настоящей статье рассматривается способ оценки уровня помех, наводимых в цепях БА КА под действием ЭСР вблизи корпуса. Рассмотрим источник помех, то есть ЭСР. Сила тока разрядного импульса имеет вид [2]

i_P(t) = I . (e p t - e p ² t )

где t – время; I , p 1 , p 2 можно найти по известным значениям амплитуды импульса, длительности импульса по уровню 0,5 и длительностью фронта по уровням 0,1…0,9. На рис. 1, как пример, представлена временная диаграмма импульса разрядной силы тока при минимальном значении длительности фронта импульса, минимальном значении переднего фронта и максимальной амплитуде 100 А.

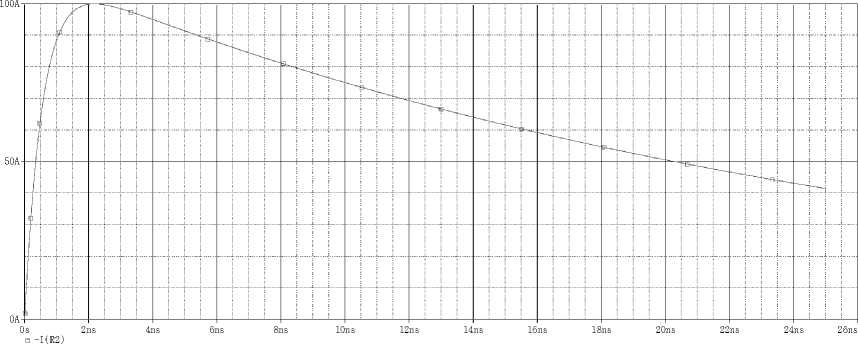
Time

Рис. 1. Временная диаграмма импульса разрядной силы тока

ЭСР можно представить в виде элементарного электрического излучателя (диполя Герца). Поскольку размеры КА соизмеримы с длинами волны спектра излучаемого ЭСР [2], то можно сказать, что приёмник помех (то есть БА) будет расположена в ближней зоне диполя Герца. Запишем выражения для напряжённостей электрического и магнитного полей в ближней зоне диполя Герца [3]:

LQco^lsin^O^

H ^ —----------;

47rr2

. Hja^lcos^')

JWSqZ^T

. tp(ja))lsin(6)

6 }WE04nr3 '

где to - угловая частота, I( j®) - спектральная плотность импульса разрядного тока, ε 0 – электрическая постоянная, l – длина вибратора, r, θ, φ – координаты сферической системы (см. рис. 2). Если подвергнуть выражение для составляющей магнитного поля обратному преобразованию Фурье, то можно увидеть, что форма импульса не поменялась, осталась такой же, что и в (1), а изменился лишь коэффициент перед выражением.

Теперь рассмотрим пример расчёта помехи. Пусть имеется токовый контур, расположенный на расстоянии R от дуги ЭСР. Контур имеет размеры a и b (см. рис. 2). На практике токовыми контурами могут являться контуры, образованные источниками сигналов, нагрузкой, сигнальным и общим проводом. Именно эти цепи являются приёмниками помех. Поскольку в реальной аппаратуре монтаж, как правило, лежит в плоскости, то предположим, что рассматриваемый контур тоже лежит в одной плоскости. В той же плоскости лежит дуга ЭСР. Ориентация, представленная на рис. 2, является самым худшим вариантом, т. к. составляющая магнитного поля нормальна плоскости контура. Найдём ЭДС помехи, наводимую в этом контуре при ЭСР.

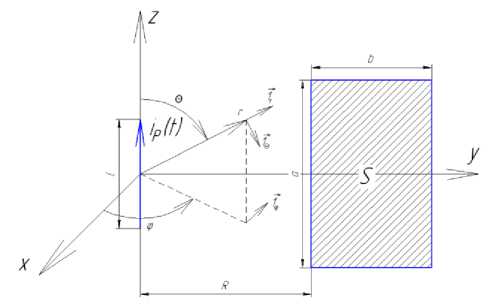
Рис. 2. Диполь Герца в декартовой и сферической системе координат и ориентация токового контура

ЭДС, наводимая в токовом контуре, может быть определена по закону Фарадея [3]

e(t) =- ^d B ^→ (t)dS ^→ =- µ ^d H ^→ (t)d ^→ S ^dtS ⁰ ^dtS , (4)

где μ 0 – магнитная постоянная, – магнитная индукция. Выражение (4) справедливо для воздуха и вакуума. Раскроем интеграл по поверхности S в декартовой системе координат [4]:

e(t) =

P- 0 ' ^ 4 n

a/ 2 R + b

- a/ 2 R

( y ² ⁺ z ²)

dydz • I • (p_}e'^P - p₂e^p ² t ).

Определим l по кривой Пашена [5], представленной на рис. 3. Напряжение ЭСР может достигать 20 кВ. По кривой Пашена определяем максимальный промежуток, при котором может произойти разряд при разности потенциалов 20 кВ. Найденное значение и будет являться l . В нормальных условиях атмосферное давление составляет от 630 до 800 мм рт. ст. При меньшем давлении значение l будет больше. При давлении 630 мм рт. ст. l =0,63 см.

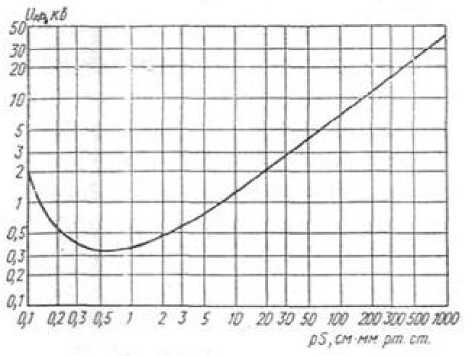
Рис. 3. Кривая Пашена для воздуха

Форма импульса наведённой ЭДС представлена на рис. 4. Поскольку ЭДС пропорциональна скорости изменения магнитного потока, а значит и тока, самый большой выброс получается во время фронта. Если провести расчёт для контура на расстоянии R=50 мм с размерами сторон a и b от 10 до 100 мм с шагом 10 мм при воздействии импульса длительностью 1 мкс по уровню 0,5, длительностью фронта 1 нс по уровню 0,1-0,9, то получим значения ЭДС, приведённые в таблицах 1 и 2. При этом длительность t1 будет равна 3,36 нс.

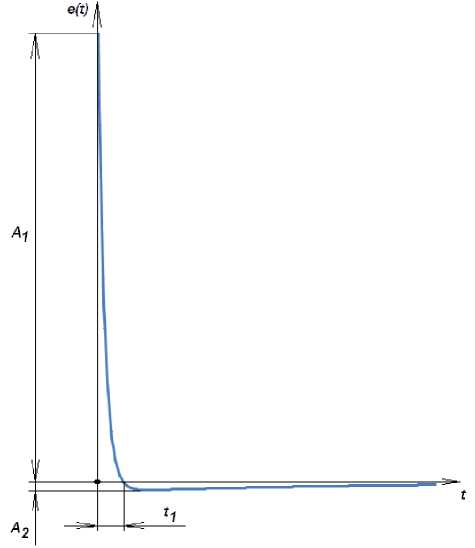
Рис. 4. Форма импульса ЭДС, наводимой в контуре

Таблица 1. Амплитуда А 1 для импульса с длительностью 1 мкс по уровню 0,5 и длительностью переднего фронта 1 нс по уровню 0,1-0,9

”\a, cm b, cm	1	2	3	4	5	6	7	8	9	10
1	4.601	9.088	13.363	17.349	20.997	24.286	27.217	29.805	32.078	34.064
2	7.891	15.61	23.006	29.958	36.384	42.244	47.527	52.251	56.449	60.164
3	10.36	20.517	30.285	39.52	48.118	56.022	63.213	69.704	75.527	80.729
4	12.282	24.34	35.972	47.014	57.349	66.909	75.667	83.628	90.826	97.306
5	13.82	27.403	40.535	53.041	64.794	75.718	85.778	94.978	103.345	110.925
6	15.078	29.911	44.277	57.991	70.922	82.985	94.143	104.394	113.764	122.296
7	16.127	32.004	47.4	62.129	76.052	89.081	101.174	112.326	122.562	131.922
8	17.015	33.775	50.047	65.638	80.407	94.264	107.162	119.095	130.084	140.169
9	17.776	35.294	52.317	68.651	84.151	98.724	112.321	124.935	136.585	147.309
10	18.436	36.611	54.287	71.266	87.403	102.601	116.812	130.025	142.257	153.548

Таблица 2 . Амплитуда А 2 для импульса с длительностью 1 мкс по уровню 0,5 и длительностью переднего фронта 1 нс по уровню 0,1-0,9

Ха, см	1	2	21	4	5	6	7	8	9	10
1	-1.364'10-3	-2.695'10-3	-3.962'10-3	-5.144'10-3	-6.226'10-3	-7.201'10-3	-8.07'10-3	-8.837'10-3	-9.511'10-3	-0.01
2	-2.34'10-3	-4.628'10-3	-6.821'10-3	-8.882'10-3	-0.011	-0.013	-0.014	-0.015	-0.017	-0.018
3	-3.072'10-3	-6.083'10-3	-8.98'10-3	-0.012	-0.014	-0.017	-0.019	-0.021	-0.022	-0.024
4	-3.642'10-3	-7.217'10-3	-0.011	-0.014	-0.017	-0.02	-0.022	-0.025	-0.027	-0.029
5	-4.098'10-3	-8.125'10-3	-0.012	-0.016	-0.019	-0.022	-0.025	-0.028	-0.031	-0.033
6	-4.471'10-3	-8.869'10-3	-0.013	-0.017	-0.021	-0.025	-0.028	-0.031	-0.034	-0.036
7	-4.782'10-3	-9.489'10-3	-0.014	-0.018	-0.0221	-0.026	-0.021	-0.033	-0.036	-0.039
8	-5.045'10-3	-0.01	-0.015	-0.019	-0.024	-0.028	-0.032	-0.035	-0.039	-0.042
9	-5.271'10-3	-0.01	-0.016	-0.02	-0.025	-0.029	-0.033	-0.037	-0.04	-0.044
10	-5.466'10-3	-0.011	-0.016	-0.021	-0.026	-0.03	-0.035	-0.039	-0.042	-0.046

Как видно из табл. 1 и 2 амплитуды импульсов могут достигать существенной величины. При увеличении длительности фронта значение А 1 уменьшается, а t 1 увеличивается. Это связано с уменьшением скорости и увеличением времени нарастания импульса тока ЭСР. Однако, корпуса БА КА, которые, как правило, изготавливаются из электропроводящего материала и ослабляют электромагнитное поле.

Как показывают расчёты [6] эффективность экранирования в некоторых диапазонах может достигать свыше 40 дБ. На амплитуду и форму импульсов ЭДС могут влиять не только корпуса БА. Поэтому, при определении помех от ЭСР предложенным в настоящей статье способом необходимо помнить, что контуры имеют собственное комплексное сопротивление (активное и реактивное). Реальную форму импульса необходимо определять с учётом этого комплексного сопротивления. Для определения комплексного сопротивления необходимо рассматривать конкретные случаи, конструкцию конкретной БА. Влияние комплексного сопротивления может привести к кардинальным изме- нениям не только амплитуд но и формы импульса вплоть до превращения его в колебательный процесс.

Список литературы Расчёт помех в цепях бортовой аппаратуры космических аппаратов, вызванных электростатическими разрядами

Manoranjan, R. J. Aeronaut. Soc.India. 1976. 28, №4. P. 431-434.
Соколов, А.Б. Обеспечение стойкости бортовой радиоэлектронной аппаратуры космических аппаратов к воздействию электростатических разрядов/А.Б. Соколов. Диссертации на соискание уч. степ. докт. техн. наук. -М.: МИЭМ, 2009. 51 с.
Макаров, Г.Т. Электродинамика и распространение радиоволн/Г.Т. Макаров, Б.М. Петров, Г.П. Грудинская. -М.: Сов. радио, 1969. 376 с.
Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов/И.Н. Бронштейн, К.А. Семендяев. -М.: Наука, Гл. ред. физ.-мат. лит., 1986. 544 с.
Техника высоких напряжений: Курс лекций для бакалавров направления 140200 «Электроэнергетика» -Томск: ТПУ, 2005. 128 с.
Полонский, Н.Б. Конструирование электромагнитных экранов для радиоэлектронной аппаратуры/Н.Б. Полонский. -М.: Сов. радио, 1979. 216 с.