Расчёт предельных характеристик электризации сопла в потоке продуктов сгорания топлива "керосин + жидкий кислород"
Автор: Онуфриев В.В., Крамаренко Р.М.
Журнал: Космическая техника и технологии @ktt-energia
Рубрика: Тепловые, электроракетные двигатели и энергоустановки летательных аппаратов
Статья в выпуске: 2 (45), 2024 года.
Бесплатный доступ
Актуальным является вопрос исследования электрофизических характеристик высокоэнтальпийного сверхзвукового потока продуктов сгорания. Работа посвящена расчёту электризации стенки сопла жидкостного р акетного двигателя при взаимодействии со сверхзвуковым потоком продуктов сгорания топлива «керосин + жидкий кислород». Проведено расчётное исследование характеристик сверхзвукового потока в закритической части сопла жидкостного ракетного двигателя, получено распределение электрического потенциала в пристеночной области сопла.
Жидкостный ракетный двигатель, скорость истечения, температура, продукты сгорания, электризация стенки сопла, амбиполярный потенциал
Короткий адрес: https://sciup.org/143183275
IDR: 143183275 | УДК: 621.45.032.5:537.21+662.613.55
Текст научной статьи Расчёт предельных характеристик электризации сопла в потоке продуктов сгорания топлива "керосин + жидкий кислород"

ОНУФРИЕВ В.В.

КРАМАРЕНКО Р.М.
ОНУФРИЕВ Валерий Валентинович — доктор технических наук,
Модель расчёта потенциала и токопереноса в пристеночном слое сопла жидкостного ракетного двигателя
Одним из основных источников зарядов статического электричества являются реактивные двигатели, выбрасывающие через сопло поток продуктов сгорания (ПС) с заряженными частицами [1–19]. Этот эффект может быть причиной электрических пробоев, возмущающего воздействия, помех в системах управления и радиосвязи и т. д. В связи с этим проведение практических работ по двигательной электризации требует расчётных моделей для проектирования и оценки указанных эффектов на работу двигателей.
Течение потока в жидкостных ракетных двигателях (ЖРД) имеет двумерное распределение, поэтому для точного решения необходимо использовать в расчётах как осевые, так и радиальные распределения компонент потока. Такой подход требует громоздких вычислений с использованием уравнений в частных производных, учёт большого количества химических реакций и уравнений газовой динамики.
При характерных температурах потока ПС в камере сгорания (КС) ЖРД (применительно к ЖРД РД-191 топливо — «керосин + жидкий кислород») основной механизм образования и рекомбинации заряженных частиц — химические реакции следующего типа:
СН + О ^ СНО + + е ;
СНО + + Н 2 ^ Н 3 О + + СО; >
Н 3 О + + е ^ Н 2 О + О.
В общем случае для расчёта электрофизических характеристик потока ПС надо знать осевые и радиальные распределения концентраций из решения уравнений химической термодинамики. Качество расчёта ионизационного состава потока ПС определяется с учётом большого количества уравнений химических реакций ионизации и рекомбинации типа (1), которые позволят получить наиболее точные распределения концентраций компонентов потока ПС вдоль сопла и по радиусу его сечений. В процессе расширения потока в сопле ЖРД температура тяжёлых частиц Тh падает из-за превращения энергии теплового движения в энергию направленного движения со скоростью u. Упругие столкновения между электронами и ионами будут приводить к уменьшению температуры электронов, а это, в свою очередь, к рекомбинации плазмы. Изменение поперечного сечения потока и уменьшение плотности частиц будут приводить (хотя и в меньшей степени) к уменьшению плотности электронов. Скорость, с которой набирают энергию свободные электроны в процессе рекомбинации, определяется по следующей формуле:
R = –ε
n е
иониз
dn
е dt ,
где εиониз — энергия ионизации нейтрала; nе — концентрация электронов в сечении сопла по потоку, поэтому температура электронов Те будет выше температуры тяжёлых частиц Тh (поток двухтемпературный). Таким образом, если градиенты малы и выполняются условия локальной «стационарности», то величина ( Те – Тh ) должна удовлетворять следующему уравнению:
m
–ε иониз
dn е = n 3 k(Т – Т)∑ 2 eν– δ , dt е 2 е h h m eh ну
где k — постоянная Больцмана; me — масса электрона; mh — ма с са тяжёлых частиц (нейтралов и ионов); v eh — средняя частота столкновений электронов с тяжёлыми частицами; δну — коэффициент неупругих потерь [20].
При выполнении условия малости тепловой энергии электронов по сравнению с энергией ионизации (kТe ≪ eεиониз, где e — заряд электрона) можно считать, что концентрация нейтралов nh, которая связана со скоростью убыли концентрации
объёме
dn е dt ,
электронов в единичном не зависит от степени ионизации αi [21, 22].
При наличии внешнего
электричес-
кого поля (например, в электродуговом двигателе) радиальные распределения температуры нейтралов и заряженных частиц в сечении сопла можно получить на основе модели, описанной в работах [11–15].
В условиях сопла ЖРД уравнение относительного теплового потока в стенку (в радиальном направлении) приводится к следующему виду:
q = –λ + n V (ε + kТ ) – e e иониз 2 е
– n V (ε + 5 kТ ) + q , (4)
h h дисс 2 h изл где λ — полная теплопроводность плазмы (всех частиц); εдисс — энергия диссоциации частиц в потоке; Ve, Vh — направленные скорости электронов и нейтралов соответственно; qизл — тепловой поток излучения.
Расчёт радиальных распределений концентрации и температуры компонент ПС в закритической части сопла позволяет получить точное решение относительно потенциала сопла вследствие амбиполярной диффузии с учётом рекомбинационных процессов. Решение уравнения (4) требует знания констант скоростей химических реакций с учётом неравновесности, процессов излучения в неравновесном потоке ПС. Это требует значительного времени численного эксперимента и его валидации по экспериментальным данным.
В рамках данной работы приведён аналитический расчёт, базирующийся на одномерной модели течения ПС, который позволяет получить оценку величин по порядку (значения потенциалов). Основным допущением в предлагаемом подходе является постоянство температуры, концентрации электронов и ионов по сечению потока ПС в его ядре, а также среднемассовой скорости потока u ( x ), а их изменения происходят у стенки: в бесстолкновительной области толщиной δ0 и амбиполярном слое толщиной δамб (рис. 1). Именно параметры частиц в этих областях и будут определять величину падения потенциала между ядром потока и стенкой (электризация стенки сопла вследствие амбиполярной диффузии).
При этом в направлении стенки сопла (перпендикулярно скорости u(х) по координате y — по радиусу сечения, рис. 1) возникает диффузионное движение заряженных частиц — электронов и ионов. Вследствие высокой подвижности электронов на стенке возникает отрицательный электрический потенциал, под действием которого потоки электронов и ионов выравниваются [21, 22]. Такой случай реализуется, если стенка сопла является непроводящей (диэлектриком). В условиях реального ЖРД стенка сопла металлическая, она является проводником, поэтому необходимо учитывать характер токопереноса в сечениях dx по длине сопла. Так как степень ионизации и электропроводность потока ПС незначительные, влиянием указанного эффекта при оценочном расчёте пренебрежём.
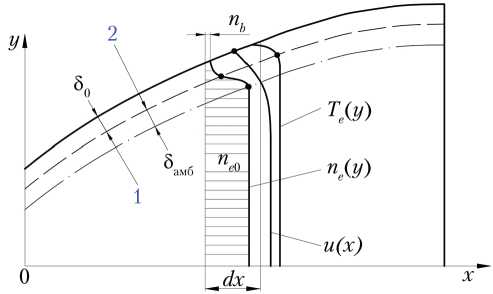
Рис. 1. Расчётная схема для оценки амбиполярного потенциала: 1 — «двойной слой» бесстолкновительный;
2 — область амбиполярной диффузии; x — длина сопла; y — радиус сечения сопла; nе(y), Te(y) — распределение концентрации и температуры электронов по сечению потока соответственно; u(x) — распределение профиля скорости потока в пристеночном слое; nb и ne 0 — концентрация электронов на стенке и в данном сечении сопла соответственно; dx — элементарный элемент по длине сопла; δ амб и δ 0 — толщина области амбиполярной диффузии и бесстолкновительной зоны соответственно (рисунок создан авторами)
В качестве допущения в модели принято постоянство концентрации заряженных частиц в ядре потока, изменение происходит в амбиполярной области. Температура электронов в амбиполярной области постоянна.
Для аналитической оценки амбиполярного потенциала на стенке сопла в первом приближении можно воспользоваться данными термодинамического расчёта параметров потока ПС как равновесного в программном комплексе TERRA [23], который даёт необходимые данные по значениям концентраций нейтралов nh , ионов ni и электронов ne , температуре и скорости ПС по длине сопла.
Отметим, что степень ионизации потока в закритической части сопла ЖРД низкая (αi ≈ 10–10…10–8, т. е. ni ≈ ne ≪ nh), что обусловлено химическим характером ионизации и высокой скоростью рекомбинации заряженных частиц при указанных температурах потока ПС (табл. 1).
Таблица 1
Распределение температуры потока продуктов сгорания, концентрации электронов, ионов и нейтралов по длине закритической части сопла для топлива «керосин + жидкий кислород» при p КС = 5 МПа, α = 0,7
|
x , м |
π |
T ПС,К |
ne 0 , м–3 |
ni 0 , м–3 |
nh 0 , м–3 |
|
0 |
1,000 |
2 975 |
7,88591·1018 |
7,88588·1018 |
2,84756·1026 |
|
0,350 |
7,157 |
2 632 |
4,26716·1015 |
4,26716·1015 |
1,56899·1025 |
|
0,700 |
14,596 |
2 316 |
1,63596·1014 |
1,63596·1014 |
7,04018·1024 |
|
1,050 |
23,073 |
2 114 |
1,34314·1013 |
1,34314·1013 |
4,26581·1024 |
|
1,400 |
30,675 |
1 993 |
2,43766·1012 |
2,43765·1012 |
3,13619·1024 |
|
1,711 |
37,000 |
1 912 |
7,01835·1011 |
7,01835·1011 |
2,53933·1024 |
Примечание. p КС — давление в камере сгорания; α — коэффициент избытка окислителя; x — координата от критического сечения по длине сопла; π — степень расширения сопла; T ПС — температура потока продуктов сгорания; ne 0, ni 0, nh 0 — концентрация в данном сечении сопла электронов, ионов и нейтралов соответственно.
Температура потока продуктов сгорания по длине от критического сечения до среза сопла снижается в 1,5 раза, что существенно увеличивает скорость рекомбинации частиц и снижает концентрацию заряженных частиц у среза. Поток ПС практически электронейт-рален по всему соплу.
Поле в амбиполярной области и пристеночном бесстолкновительном слое тормозит электроны и ускоряет ионы. При расчёте плотности потока диффузии предполагается, что его величина пропорциональна градиенту концентрации заряженных частиц — электронов.
Поток диффузии электронов в радиальном направлении в сопле определяется следующим образом [12–15]:
n nV = –D e = –D e e амб дn дT ee
амб д T e д y ,
где D амб — коэффициент амбиполярной диффузии.
В этом случае движение заряженных частиц в пристеночном слое в одномерном приближении описывается следующим образом:
- en E (y) - e " - mnv {Q,)( V - V,) n, = 0; e e e e eh e h h enE(У) - dpi- - mnv
где pe , pi — давление электронов и ионов соответственно; Vi — направленная скорость ионов; ve , vi — тепловые скорости компонент плазмы (электронов и ионов соответственно); Е — напряжённость поля в пристеночном (амбиполярном) слое; < Qeh ), < Qh ) — сечения столкновений с нейтралами электронов и ионов соответственно.
Так как выполняется соотноше- ние между скоростями частиц в слое
(Vi ≫ Vh; Ve ≫ Vh), систему (6) можно записать следующим образом:
– eneE
dp
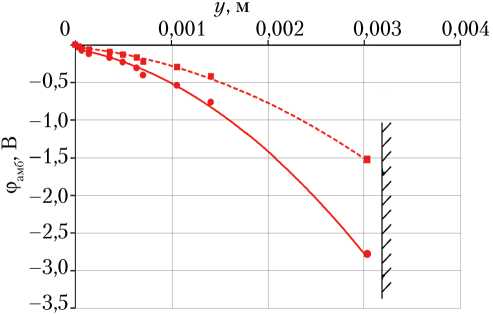
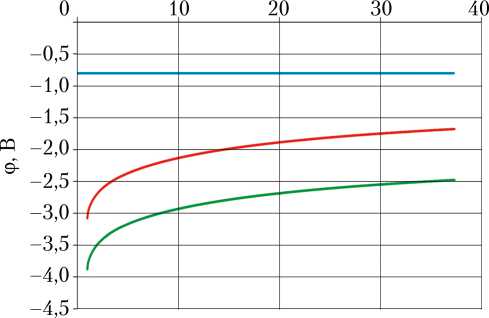
—^ - mnv < Q ,) V n, = 0; e e e eh e h enEPi- - mnv Если ввести плотность тока je = –eneVe, то получим для электронов уравнение в следующем виде: dp je -eneE-~d^+ — < Qeh>vnm = 0’ (8) Для оценочного расчёта (верхний предел значения амбиполярного потенциала) область ядра потока ПС рассматриваем с фиксированными значениями температур заряженных частиц Те,i,h(y) = const и их концентрациями, т. е. в данной аналитической модели амбиполярный потенциал оценивался по пристеночному слою. В амбиполярной области выполняется условие | j | = | je I, а в силу низкой электропроводности ст потока ПС ^ ^ 0, в уравнении (8) остаются первое и второе слагаемые, позволяющие рассчитать напряжённость поля: eneE(y) ≈ – dpe , e dy т. е. градиент электронного давления в слое создаёт электрическое поле, связанное с амбиполярной диффузией. Так как при оценочном расчёте температура электронов в пределах амбиполярного слоя может быть принята постоянной, поле определяется градиентом концентрации электронов. Поэтому решение в безразмерном виде для распределения плотности электронной компоненты в амбиполярном слое может быть выражено на основе классического подхода [21, 22]: d2n 2е dy2 где ne — электронов, полярного ne(1 – ne2), относительная n e пе (у ) N о ’ y — концентрация толщина амби- слоя, y = lR lR — длина диффузии иона. Значения концентрации электронов ne0 в данном сечении сопла ракетного двигателя по оси потока продуктов сгорания получены расчётом в программном комплексе TERRA [23] (см. табл. 1) для известных компонент топлива (в нашем случае «керосин + жидкий кислород») и давления в камере сгорания ЖРД, а также геометрии сопла. В качестве геометрической модели использована закритическая часть сопла ЖРД РД-191. Величина ne представляет собой относительную концентрацию электронов — отношение концентрации ne(у) в данной точке по y в приповерхностной области вблизи стенки к кон- центрации в ядре потока ne0. Величина lR, в соответствии с работами [21, 22], может быть определена следующим образом: R D амб п 22 Р( Т ) e0 e где Daмб обусловлен подвижностями ионов pi и электронов p e; Р( Те) коэффициент. Для интегрирования выражения (10) введём следующее преобразование: d n е dy2 d (dn У е dn dy е Поэтому выражение (12) можно заменить на следующее уравнение: dnе 1 – ne2 dy 2 Граничные условия уравнения (13): • для ядра потока y = 0; n = 1; dnе = 0; dTe = 0; e dy dy– • для стенки сопла y = yb; ne = nb, где yb — толщина амбиполярного слоя; nb — относительная концентрация ионов на стенке; полагаем, что в бесстолкновительной области — «двойном слое» — концентрация электронов изменяется по закону Больцмана (см. рис. 1). Решение уравнения (13) с учётом граничных условий можно получить прямым интегрированием в следующем виде [21]: по длине х закритической части сопла вдоль его оси протяжённостью 0,005 м каждый. При расчётах относительная концентрация электронов на стенке сопла задавалась значением nb = 10–4. Максимальная величина потенциала на амбиполярном слое ϕамб достигается в головке закритической части сопла и составляет порядка –3,08 В (табл. 2), а на срезе сопла значение амбиполярного потенциала по модулю снижается почти в два раза. Уменьшение амбиполярного потенциала связано со снижением концентрации заряженных частиц по длине сопла при расширении потока ПС, сопровождающемся переходом внутренней энергии потока в кинетическую энергию с уменьшением температуры и степени ионизации ПС. В условиях данной задачи, когда нет внешнего источника поля (в качестве сторонних сил выступает градиент электронного давления), ток на стенку сопла стремится к нулю, поэтому распределение потенциала можно оценить по следующему уравнению [21, 22]: dф dy kT e e H e — H i , He + Hi ; d lnn . dy e _ 1 - exp[-(y -yb)] nе ≈ . е1 + exp[-(y —Уь)] Проинтегрировав выражение (15), получим величину потенциала на амбиполярном слое (знак минус показывает, что стенка заряжается отрицательно): Следует учесть, что относительная концентрация электронов на стенке nb = 10–5…10–3 [21, 22]. Отметим, что численное изменение концентрации электронов на стенке на два-три порядка несущественно сказывается на изменении величины амбиполярного потенциала, который в этом случае возрастает в два-три раза, что позволяет по выражению (14) выполнить оценку величины амбиполярного потенциала. При характерной длине рекомбинации иона в амбиполярной области lR = 10–3 м [из формулы (11)] величина относительной концентрации электронов на стенке составляет nb = 10–4. Характерная глубина амбиполярной области составляет yb = 3lR …4lR [21]. Результаты расчёта амбиполярного потенциала в слое (потока ПС «керосин + жидкий кислород») приведены в табл. 2. Расчёт был выполнен для 344 шагов Фамб — Ф(О) = — — [’"^in ~, (16) E ^e + "J Пь где ϕ(0) — потенциал ядра потока ПС. С учётом ϕ(0) = 0, формулу (16) можно записать следующим образом: ϕ амб kT n E^e ^i ln e 0 E ^E + ^j ПЬ kT e e lnn . b Отметим, что потенциал стенки сопла от амбиполярной диффузии ϕамб — отрицательный. В процессе расширения потока уменьшается его температура, степень ионизации снижается (см. табл. 1) почти на три-четыре порядка, т. е. рекомбинация становится превалирующим процессом, определяющим значение амбиполярного потенциала. Таблица 2 Результаты расчёта амбиполярного потенциала по длине сопла для топлива «керосин + жидкий кислород» при pКС= 25 МПа, α = 0,7 –n e _ y у, м Потенциал в амбиполярном слое ϕамб, В при π = 1,000; x = 0 м при π = 7,157; x = 0,350 м при π = 14,596; x = 0,700 м при π = 23,073; x = 1,050 м при π = 30,675; x = 1,400 м при π = 37,000; x = 1,711 м 1,0000 0 0 0 0 0 0 0 0 0,9000 0,05 0,00003 –0,0351 –0,0260 –0,0229 –0,0210 –0,020 –0,019 0,8000 0,10 0,00007 –0,0750 –0,0550 –0,0484 –0,0459 –0,042 –0,041 0,7000 0,20 0,00014 –0,1190 –0,0870 –0,0774 –0,0710 –0,067 –0,065 0,6000 0,50 0,00035 –0,1710 –0,1250 –0,1110 –0,1020 –0,097 –0,093 0,5000 0,70 0,00049 –0,2320 –0,1690 –0,1500 –0,1380 –0,131 –0,126 0,4000 0,90 0,00063 –0,3060 –0,2241 –0,1990 –0,1831 –0,173 –0,167 0,3000 1,00 0,00070 –0,4020 –0,2940 –0,2610 –0,2400 –0,228 –0,219 0,2000 1,50 0,00106 –0,5380 –0,3930 –0,3490 –0,3210 –0,304 –0,293 0,1000 2,50 0,00141 –0,7700 –0,5620 –0,5000 –0,4600 –0,436 –0,412 0,0001 4,50 0,00318 –3,0790 –2,2450 –1,9990 –1,8380 –1,742 –1,678 Примечание. За ноль принята точка на оси потока; pКС — давление в камере сгорания; α — коэффициент избытка окислителя; –ne — относительная концентрация электронов; –y — толщина амбиполярного слоя; y — глубина слоя от ядра потока; π — степень расширения сопла; x — текущая координата элемента объёма продуктов сгорания вдоль оси сопла от критического сечения. Распределение амбиполярного потенциала в слое (в элементе потока частично ионизованной плазмы ПС длиною dx) показано на рис. 2. На рис. 3 показано изменение амбиполярного потенциала на стенке по степени расширения потока ПС в сопле. Таким образом, максимальное результирующее значение потенциала на стенке сопла от амбиполярной диффузии составляет –3,08 В. При расчёте не учитывалось радиальное распределение концентраций в ядре потока, так как расчёт носит оценочный характер. Аналогичные расчёты по определению амбиполярного потенциала и параметров потока частично ионизованной плазмы ПС проведены для варианта дросселирования тяги РД-191 при разных значениях давления в КС. Результаты расчёта амбиполярного потенциала электризации на стенке сопла ЖРД РД-191: • при pКС = 25 МПа ϕамб = –3,08 В; • при pКС = 15 МПа ϕамб = –3,02 В; • при pКС =10 МПа ϕамб = –2,98 В. Рис. 2. Изменение потенциала по глубине амбиполярного слоя ϕамбдля топлива «керосин + жидкий кислород» при давлении в камере сгорания 25 МПа и коэффициенте избытка окислителя 0,7: к — критическое сечение (п = 1, x = 0 м); ■ ■ ■ — сечение (п = 37, x = 1,711 м); стенка показана справа (рисунок создан авторами) Дополнительно нужно учесть падение потенциала на «двойном слое» толщиной δ0 (см. рис. 1) Δϕ1 (в бесстолкновительной области у поверхности стенки), которое определяется логарифмом корня из отношения масс иона и электрона. Оценки показывают, что его величина Δϕ1 ≤ – 1,0 В (рис. 4). Рис. 3. Изменение амбиполярного потенциала ϕамб в зависимости от степени расширения сопла π для топлива «жидкий кислород + керосин» при давлении в камере сгорания 25 МПа и коэффициенте избытка окислителя 0,7 (рисунок создан авторами) Проведённые аналитические расчёты по прямой оценке потенциала электризации сопла ЖРД показали, что его величина составляет порядка –3…–4 В (рис. 4). Рис. 4. Распределение амбиполярного потенциала Фамб (м), потенциала на двойном слое Лф1 (™) и потенциала стенки сопла фстенки = Фамб + Лф1 (м) в зависимости от степени расширения сопла π (рисунок создан авторами) Аналогичный характер образования потенциала на стенке сопла модельных ракетных двигателей получен в работах [16–19; 24–26] при использовании другого топлива («спирт + воздух», «метан + воздух» и др.). В частности, авторами работы [26] установлено, что глубина амбиполярного слоя составляет 3…5 мм от стенки сопла. Количественное совпадение размеров пристеночного слоя подтверждает правомерность модели для аналитической оценки потенциала электризации. В процессе исследования электризации сопла модельного ЖРД на топливе «этанол + кислород» при давлении в КС 3 МПа при температуре ПС от 2 000 до 2 500 К [26] зарегистрирован потенциал сопла ~ –0,2 В. Заключение В процессе расчётно-аналитического исследования электризации сопла потоком ПС топлива «керосин + жидкий кислород» применительно к геометрии ЖРД РД-191 выявлено, что основным процессом накопления заряда на стенке является диффузия электронов из ядра потока вследствие градиента электронного давления, которая уравновешивается создаваемым ею потенциалом. Величина потенциала на стенке сопла ЖРД составляет порядка –3…–4 В. Добавим, что в условиях взаимодействия остывающего потока ПС при его течении по соплу амбиполярный потенциал, возникающий на стенке, по модулю снижается почти в два раза вследствие резкого уменьшения концентрации заряженных частиц (превалирующий процесс — рекомбинация). Работа выполнена при поддержке Проекта № 0705-2020-0044 фундаментальных научных исследований Минобрнауки РФ.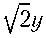
Список литературы Расчёт предельных характеристик электризации сопла в потоке продуктов сгорания топлива "керосин + жидкий кислород"
- Lawton J., Weinberg F. Electrical aspects of combustion. Oxford: Oxford University Press, 1969.
- Balwanz W.W. Thermal ionization of rocket exhaust plasmas: Naval Research Laboratory report 5808. July 30, 1962.
- Balwanz W.W. Ionization in rocket exhausts // 10th Symposium (International) on Combustion. The Combustion Institute, 1965. U. S. Naval Research Laboratory, Washington. P. 685–697.
- Balwanz W.W. Radiation from rocket exhausts // Proceedings of 4th Naval Science Symposium “Naval Problems in Electromagnetic Radiation”. Office of Naval Research Report ONR-6, March 9–11, 1960.
- Lawton J, Weinberg FJ. [Electrical aspects of combustion Oxford]. Moscow: Energia, 1976 (in Russian).
- Yin Y, Cai J, Zuo H, Mao H, Fu Y, Yan H. Experimental investigation on electrostatic monitoring technology for civil turbofan engine. Journal of Vibroengineering. 2017; 19(2): 967−987. Available from: https://doi.org/10.21595/jve.2016.17273 (accessed 30.09.2023).
- Mekker G. Dvizhushchayasya plazma [Moving plasma]. Moscow: Foreign literature publishing house; 1961 (in Russian).
- Devoto RS. Transport properties of partially ionized hydrogen. Journal of Plasma Physics. 1968; 2(4): 617–631. Available from: https://doi.org/10.1017/S0022377800004086 (accessed 30.09.2023).
- Nazarenko IP, Nikrityuk PA. The Effect of the Arc Channel on the Transport Properties of Hydrogen Electric-Arc Plasma. High Temperature. 2003: 41(3): 290–294. Available from: https://doi.org/10.1023/A:1024269905899 (accessed 30.09.2023).
- Leung K, Nielsen IMB, Criscenti LJ. Elucidating the bimodal acid−base behavior of the water−silica interface from first principles. Journal of the American Chemical Society. 2009; 131(51): 18358–18365. Available from: https://doi.org/10.1021/ja906190t (accessed 30.09.2023).
- Aronowitz L. Electrostatic potential generated by rockets on vehicles in space. IEEE Transactions on Electromagnetic Compatibility. 1968; EMC-10(4): 341–346.
- Vatazhin AB, Grabovskii VI, Likhter VA, Shul’gin VI. Elektrogazodinamicheskie techeniya [Electrogasdynamic flows]. Moscow: Nauka publishers; 1983 (in Russian).
- Nazarenko IP, Nikrityuk PA. Effect of thermochemical disequilibrium on the composition of a hydrogen arc plasma. High Temperature. 2002; 40(6): 795–800. Available from: https://doi.org/10.1023/A:1021456612522 (accessed 30.09.2023).
- Nazarenko IP, Nikrityuk PA. Calculation of characteristics of hydrogen arc with due regard for thermochemical nonequilibrium. Teplofizika vysokikh temperatur [High Temperature]. 1998; 36(5): 693–699. Available from: https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=tvt&paperid=2523&option_lang=rus&ysclid=luv5nzwdff602122631 (accessed 30.09.2023) (in Russian).
- Asinovskii EI, Kirillin AV, Nizovskii VL. Stabilizirovannye elektricheskie dugi i ikh primenenie v teplofizicheskom eksperimente [Stabilized electric arcs and their use in thermophysical experiment]. Moscow: Nauka; 1992 (in Russian).
- Nagel’ YuA. K voprosu opredeleniya elektricheskogo toka strui pri istechenii plotnogo slaboionizovannogo gaza [Towards determination of electrical current of a jet during efflux of a dense slightly ionized gas]. Teplofizika vysokikh temperatur [High Temperature]. 1987; 25(6): 1246 (in Russian).
- Nagel’ YuA. Elektrizatsiya dvigatelei pri istechenii produktov sgoraniya. Eksperimental’nye rezul’taty [Electrization of engines during discharge of combustion products. Experimental results]. Zhurnal tekhnicheskoi fiziki [Journal of Technical Physics]. 1999; 69(8): 55–59. Available from: https://journals.ioffe.ru/articles/36140 (accessed 30.09.2023) (in Russian).
- Potapov GP. Elektrizatsiya reaktivnykh sopel [Electrization of exhaust nozzles]. News of High Educational Institutions. Aviation Technics. 1978; 4: 112–117 (in Russian).
- Pinchuk VA. Jet engine electrification as a phenomenon reflecting the evolution of charge instability in an outflowing combustion product mixture. Technical Physics. 1997; 42(8): 872–876.
- Ginzburg VL. Rasprostranenie elektromagnitnykh voln v plazme [Electromagnetic wave propagation in plasma]. 2nd edition, revised. Moscow: Nauka; 1967 (in Russian).
- Mitchner M, KrugerCH. [Partially ionized gases]. Moscow: Mir; 1976 (in Russian).
- Chen FF. [Introduction to plasma physics]. Moscow: Mir; 1987 (in Russian).
- Trusov BG. TERRA — modelirovanie fazovykh i khimicheskikh ravnovesii [TERRA — simulation of phasic and chemical equilibria]: methodical guidelines. Moscow: BMSTU Publishers; 2013 (in Russian).
- Kotel’nikov VA, Kotel’nikov MV, Filippov GS. Elektrofizicheskie parametry potokov plazmy, istekayushchikh iz zhidkostnykh raketnykh dvigatelei [Electrophysical parameters of plasma effluents from liquid-propellant engines]. Problemy mashinostroeniya i nadezhnosti mashin [Problems of engineering and machine reliability]. 2018; 6: 13–20. Available from: https://doi.org/ 10.31857/S023571190002556-2 (accessed 30.09.2023) (in Russian).
- Potapov GP, Dregalin AF. Obrazovanie staticheskogo elektrichestva pri istechenii iz sopla ionizirovannogo gaza [Static electricity build-up during discharge of ionized gas from the nozzle]. Izvestiya vuzov. Aviatsionnaya tekhnika [Proceedings of institutions of higher learning. Aviation engineering]. 1977; 5: 90–92 (in Russian).
- Yagodnikov DA, Voronetskii AV, Pushkin NM. Electrification of nozzle in a liquid rocket engine. Combustion, Explosion and Shock Waves. 1995; 31: 450–454. Available from: https://doi.org/10.1007/BF00789365 (30.09.2023).


