Расчёт преломляющих оптических элементов для формирования заданных распределений освещённости в прямоугольных областях с большим соотношением сторон

Формирование заданного распределения освещённости в прямоугольной области является актуальным для задач проектирования систем уличного, промышленного и жилого освещения. Задача расчёта оптического элемента, формирующего заданное распределение освещённости, состоит в определении формы его преломляющих (отражающих) поверхностей. Решение данной задачи сводится к решению нелинейного дифференциального уравнения в частных производных типа Монже-Ампера [1-3]. В общем трёхмерном случае решение данного уравнения является крайне сложным. Аналитическое решение возможно только в частных случаях с радиальной или продольной симметрией [4-10]. Для расчёта оптических элементов, формирующих заданные распределения освещённости в прямоугольной области, используются оптимизационные итерационные процедуры [11-21].

Методы [11-21] предназначены для расчёта оптических элементов, имеющих единственную рабочую преломляющую поверхность свободной формы (free-form). Использование оптических элементов такого типа для генерации заданных распределений освещённости в вытянутых прямо угольных областях приводит к существ енным потерям световой эффективности. Это связано с ограниченными возможностями рефракционной поверхности при повороте лучей на большие углы. Например, при показателе преломления материала 1,5 максимальный угол поворота луча при преломлении на границ е матери-ал-воздух составляет менее 49°.

В работе [22] предложена конструкция оптического элемента, позволяющая с высокой световой эффективностью генерировать для компактного источника излучения диаграммы направленности (ДН) в виде отрезка. Предложенная конструкция содержит две группы рабочих поверхностей. Первая группа поверхностей отвечает за преобразование сферического пучка от источника излучения в пучок с цили ндрическим волновым фронтом. Вторая группа представлена цилиндрической внешней поверхностью, которая формирует ДН в виде отрезка при цилиндрическом падающем пучке. Высокая световая эффективность формирования ДН достигается за счёт использования эффекта полного внутреннего отражения при формировании цилиндрического пучка. В работе [23] рассмотрена модификация конструкции [22] на случай формирования ДН прямоугольной формы. Необходимо отметить, что при формировании прямоугольной ДН решение [23] является приближенным. Кроме того, оно неприменимо для формирования распределений освещённости в прямо угольной области.

В данной работе для формирования вытянутых прямоугольных распределений освещённости предлагается использовать конструкцию оптического элемента [22] с внешней поверхностью свободной формы (free-form). Такая поверхность позволяет преобразовать падающий на неё цилиндрический пучок и сформировать заданное распределение освещённости в виде вытянутого прямоугольника. В работе приведён метод расчёта внешней поверхности и рассчитаны оптические элементы, формирующие равномерные распределения освещённости в прямоугольных областях с угловыми размерами 140 °х 67 ° и 140 °х 34 ° . Энергетическая эффективность рассчитанных оптических элементов составляет более 83%.

Постановка задачи

Пусть в начале координат расположен точечный (компактный) источник излучения с заданной интенсивностью излучения I ( у ) , где у - зенитный угол сферической системы координат. Задача состоит в расчёте оптического элемента, расположенного над источником излучения, из условия формирования заданного распределения освещённости

E0 (u,v) в плоскости z = f , где (u,v) - декартовы координаты в выходной плоскости.

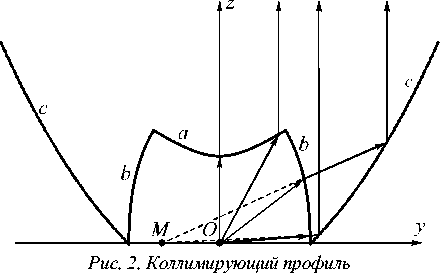
Для формирования распределений освещённости в вытянутых областях (типа прямо угольника с большим соотношением сторон) в работе предлагается использовать конструк цию оптического элемента, изображённую на рис. 1 [22]. Поверхности a , b и c получены вращением коллимирующего профиля, показанного на рис. 2, вокруг оси y . Кривая a профиля на рис. 2 является частью гиперболы и выполняет функцию коллиматора, поверхность b создаёт мнимый источник в точке M , а кривая c является частью параболы с фокусом в точке M и также коллимирует лучи от источника излучения. Поверхности a , b и c преобразуют сферический волновой фронт от источника излучения в цилиндрический волновой фронт с осью y . Расчёт этих поверхно- стей был подробно рассмотрен в [22].

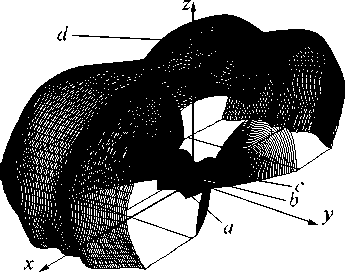
Рис. 1. Конструкция оптического элемента

Внешняя поверхность d на рис. 1 имеет свободную форму (free-form). Она должна преобразовывать цилиндрический волновой фронт от поверхностей a , b и c таким образом, чтобы в выходной плоскости формировалось распределение освещённости E ( u , v ) , максимально близкое к требуемому распределению освещённости E _o ( u , v ) .

Функция радиус-вектора внешней поверхности может быть представлена как некоторая параметризованная функция r (ф, у; с), определённая в цилиндрических координатах. Здесь ф - это угол между плоскостью, содержащей вектор направления и ось y , и плоскостью Oyz . В этом случае расчёт формы внешней поверхности d сводится к решению задачи минимизации ф ункци и нескольких переменных:

f ( с ) =| E ( u , v ; c ) - E o ( u , v )||^ min.             (1)

Расчёт распределения освещённости в выходной плоскости

Необходимым этапом решения обратной задачи, состоящей в определении вектора параметров c внешней преломляющей поверхности из условия минимума функции невязки (1), является решение прямой задачи. Прямая задача состоит в расчёте распределения освещённости в выходной плоскости при заданной внешней поверхности r ( ф , у ; с ) . Рассмотрим некоторую цилиндрическую поверхность с радиусом R и осью y , расположенную внутри оптического элемента. Так как конфигурация внутренних поверхностей оптического элемента, формирующих цилиндрический волновой фронт, известна, будем считать известным и распределение освещённости E '( ф , у ) на этой цилиндрической поверхности.

Согласно закону сохранения светового потока, световой поток d Ф , проходящий через элементарную площадку dS на цилиндрической поверхности, равен световому потоку, попавшему на соответствующий элемент с площадью dudv в выходной плоскости. С учётом френелевских потерь получим след ующее соотношение для распределений освещённости:

T ( ф , у ; с ) E ' ( ф , у ) Rd ф dy = E ( u ( ф , у ; с ) ) dudv ,

^E ( ^u ( ф , У ; ^с ) )

T ( ф , у ; ^с ) Е '( ф , у ) ^R | J ( u ( ф , у ; ^с ))|

где u ( ф , у ; с ) - точка в выходной плоскости, в которую попадает луч, прошедший через точку ( ф , у ) цилиндрической поверхности, д u д v д u д v      _

J(u(ф,у;с))=————— - якобиан перехода от дф ду ду дф координат (ф, у) к координатам (u, v). Вычисление координат точки u (ф, у; с) подробно рассмотрено в [20-21].

Используя след ующее свойство двумерной дельта-функции Дирака [24]

f (x, у)| J (u (x, у ))|

и x=x и у=у

+^ +^

x , у ) 8 ( u - u ( x , у ) , ■? - v ( x , у ) ) d x d у

—^ —^

где (x, у) - такая точка в пространстве (x, у), что u (x, у) = й, а v(x, у) = ■?, представим распределение освещённости в выходной плоскости E(u, v;c) в интегральном виде [24]:

y max П /2

E(u,v;c) = R J J T(ф,y;c)х

- y max -П /2                                      ⁽⁴⁾

x E ‘ ( ф , y ) S ( u - u ( ф , y ; c ) ) d ф d y .

Для численных расчётов заменим в (3) дельтафункцию Дирака гауссовой функцией

• 1        ( u ² + v ² )

Mu,v) = Tz^expl —I 2ПС    ^  2G j и получим следующее приближенное выражение для освещённости:

• ^y max n /2

E(u,v;c)= j j RT(ф,y;c)x

• - y max -П /2                    .                     (5)

xE ‘(ф, y )8CT (u - u (ф, y; c)) dф dy

Примеры расчёта оптических элементов

Описанный выше метод расчёта внешней поверхности оптического элемента был реализован в среде программирования Matlab^®. Преломляющая поверхность r ( ф , y ; c ) была представлена в виде бикубического сплайна [25]. В этом случае вектор параметров представляет собой набор значений функции радиус-вектора, её первых и смешанной производных в узлах сплайновой сетки. Для оптимизации параметров преломляющей поверхности применялся градиентный метод Бройдена-Флетчера-Голдфарба-Шанно [26]. В качестве функции невязки (1) использовалось относительное среднеквадратичное отклонение (ОСКО) формируемого распределения освещённости от заданного. Вычисление градиента функции невязки (1) производилось аналогично [20].

На рис. 3 изображён рассчитанный оптический элемент, формирующий равномерное распределени е освещённости в прямоугольнике со сторонами 17 мх4 м на расстоянии 3 м от ламбертовского источника излучения. Такой оптический элемент может быть использован для освещения вытянутого холла или коридора. Угловые размеры освещаемой области составляют 140°х67 . Размеры оптического элемента равны 58х21х20 мм вдоль осей х, y и z соответственно. Время расчёта составило около 24 минут на компьютере с процессором Intel® Core™ 2 Quad Q9400. На рис. 4 изображено распределени е освещённости в выходной плоскости, рассчитанное с помощью коммерческого программного обеспечения TracePro® [27] от компании Lambda Research Corporation. Световая эффективность (доля светового потока источника, попавшая в освещаемую область) рассчитанного оптического элемента составляет более 83 %. Относительное среднеквадратичное отклонение (ОСКО) формируемого распределения освещённости от равномерного распределения освещённости не превышает 9 %. Необходимо заметить, что программное обеспечение TracePro® не по- зволяет производить расчёт преломляющих поверхностей и используется в данной работе только для проверки работоспособности рассчитанных оптических элементов.

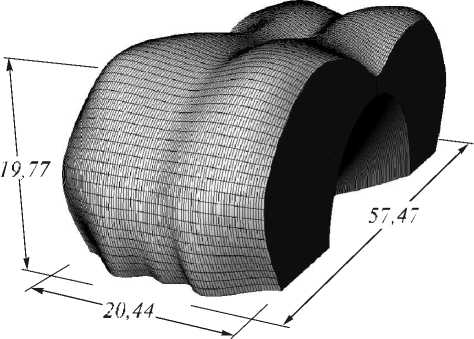
Рис. 3. Оптический элемент, формирующий равномерное распределение освещённости в прямоугольнике 17 м х 4 м

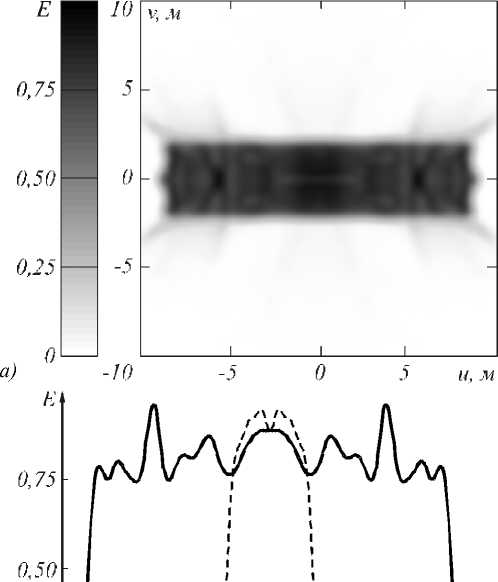
0,25

Рис. 4. Распределение освещённости в выходной плоскости от оптического элемента на рис. 3: а) полутоновое распределение;

б) сечения распределения освещённости: непрерывная линия - v = 0 , штриховая линия - u = 0 Для сравнения рассмотрим оптический элемент, имеющий единственную преломляющую рабочую поверхность и формирующий равномерное распределение освещённости с теми же параметрами, что и в предыдущем случае. На рис. 5 изображён такой

б)

оптический элемент, рассчитанный с помощью метода [20]. Размеры оптического элемента составляют 55 х 30 х 18 мм вдоль осей x , у и z соответственно.

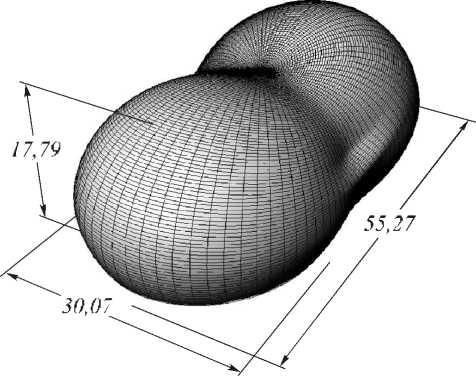
Рис. 5. Оптический элемент, формирующий равномерное распределение освещённости в прямоугольнике 17 м х 4 м и имеющий одну рабочую преломляющую поверхность

На рис. 6 изображено распределение освещённо-

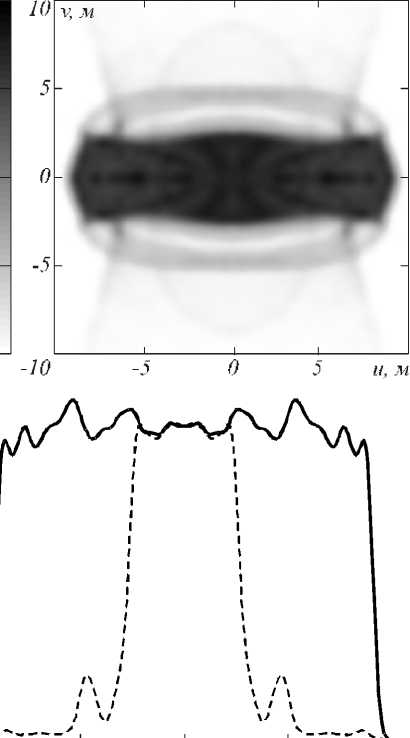
В связи с ограниченными возможностями рефракционной поверхности при повороте лучей и небольшим поперечным угловым размером освещаемой области световая эффективность оптического элемента составляет менее 60 %. ОСКО формируемого распределения освещённости равно 6,7 %. Сравнение рис. 4 и рис. 6 показывает, что при формировании распределений освещённости в прямоугольных областях с большим соотношением сторон и небольшим угловым поперечным размером метод [20] не позволяет достичь той световой эффективности, которую обеспечивает метод, представленный в данной работе.

На практике часто возникает задача формирования распределения освещённости в смещённой прямоугольной области. Примером может быть расчёт настенных светотехнических устройств, освещающих коридор или длинную комнату, фонарей уличного освещения, расположенных у края дорожного полотна и т.д. На рис. 7 изображён оптический элемент, формирующий равномерное распределение освещённости в смещённом прямоугольнике с размерами 17 м х 2 м от ламбертовского источника излучения.

сти от этого элемента, полученное с помощью программного обеспечения TracePro®.

0,75

0,50

0,25

Е

0,75

0,50

0,25

б)

Рис. 6. Распределение освещённости в выходной плоскости от оптического элемента на рис. 5: а) полутоновое распределении; б) сечения распределения освещённости: непрерывная линия - v = 0 , штриховая линия - и = 0

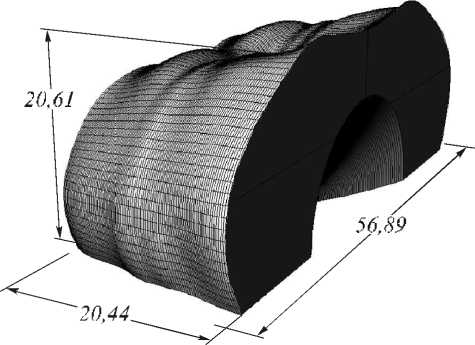
Рис. 7. Оптический элемент, формирующий равномерное распределение освещённости в смещённом прямоугольнике с размерами 17 м х 2 м

Расстояние между источником и выходной плоскостью 3 м. Центр освещаемой области лежит не на оси Oz , как в предыдущем примере, а смещён на 1 м по оси y . Размеры рассчитанного оптического эле-

мента равны 57 х 21 х 21 мм вдоль осей x, у и z соответственно. Такой оптический элемент, как и в предыдущем примере, может быть использован для освещения длинных коридоров. Время расчёта составило менее полутора часов. На рис. 8 изображено распределение освещённости в выходной пло скости, рассчитанное с помощью программного обеспечения TracePro®. Световая эффективность оптического элемента составляет более 85 %, а ОСКО формируемого распределения освещённости равно 7,9 %.

Необходимо заметить, что оптические элементы с единственной рабочей рефракционной поверхностью (рис. 5) не могут обеспечить световую эффективность выше 50 % при формировании смещённых распределений освещённости, аналогичных рис. 8. В этом слу-

чае использование рассмотренной в данной работе конструкции оптического элемента может позволить увеличить световую эффективно сть на 30-40 %.

0,25 — -5 -                                - fl I-------------                ----------------------------------1------------------------------------1----------------------------------1---------------------------------- а)        -10        -5        0       5 и, м

EK

0,75 -

0,50 b

б)

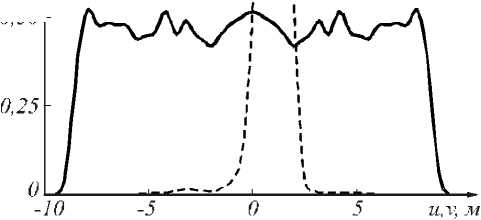
Рис. 8. Распределение освещённости в выходной плоскости от оптического элемента на рис. 7: а) полутоновое распределение; б) сечения распределения освещённости: непрерывная линия - v = 0, штриховая линия - и = 0

Рассмотренные примеры показывают, что представленный метод расчёта оптических элементов является эффективным при решении задач освещения вытянутых областей, имеющих поперечный угловой размер менее 70°.

Заключение

В работе представлен метод расчёта преломляющих оптических элементов, формирующих с высокой световой эффективностью заданные распределения освещённости в вытянутых прямо угольных областях с небольшими поперечными угловыми размерами . Рассчитаны два оптических элемента, формирующих равномерные распределения освещённости в прямоугольниках с размерами 17 мх4 м и 17 мх2 м. Угловые размеры освещаемых областей составляют 140°х67 ° и 140°х34° соответственно. Световая эффективность рассчитанных оптических элементов превышает 83 %, а ОСКО формируемых распределений освещённости составляет менее 9 %. При указанных размерах освещаемых областей предложенный метод обеспечивает увеличение световой эффективности более, чем на 20 % по сравнению с оптическими элементами, имеющими единственную рабочую преломляющую поверхность.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (гранты РФФИ 09-07-12147-офи_м, 10-02-90716-моб_ст) и гранта Президента РФ поддержки ведущих научных школ НШ-7414.2010.9.