Расчёт скольжения в межвальных роликовых подшипниках ГТД

центробежного расширения колец подшипника и деталей подшипникового узла.

Увеличение наружного диаметра центрирующей поверхности сепаратора определяется температурным расширением и центробежным расширения вращающегося сепаратора. Тогда зазор “плавания” сепаратора g пл в рабочих условиях будет равен разности диаметров центрирующих поверхностей.

Экспериментальные исследования показывают существенное влияние формы контакта торцов роликов и направляющих бортиков на проскальзывание в роликовых подшипниках. В настоящей работе рассмотрим стандартный вариант – контакт плоских торцов ролика и направляющего бортика.

На кинематику подшипника оказывает влияние также момент трения торца ролика в контакте с гнездом сепаратора. Рассмотрим также простейший вариант сепаратора в виде кольца с гнездами для роликов.

Геометрические характеристики контактов бомбинированных роликов с беговыми дорожками колец рассмотрены в [4]. В настоящей работе рассмотрим характеристики контактов колец с роликами, образующая которых описывается радиусом.

По рекомендациям [4] расчёт толщин элас-тогидродинамических смазочных слоев в контактах выполняется по формуле

Безразмерные параметры в приведенных формулах определяются соотношениями

P s = M o U v( E np R np ) ; P u = « E np ;

P n = E np R np A lp m ( i ) ; Р т = M o ^^ c .

Здесь Д о = Д о t ⁾ – динамическая вязкость смазки; « = Ор ⁾ – пьезокоэффициент вязкости смазки; Л . = A . t ) – коэффициент теплопроводности смазки; Р - коэффициент зависимости вязкости от температуры; E пр – приведенный модуль упругости в контакте; F m ( i )/А l -нагрузка на единицу длины в среднем сечении линии контакта; t c – температура смазки в зоне контакта; U ^ скорость качения в зоне трения.

Степень жидкостного трения, характеризующая наличие металлического контакта микронеровностей шероховатых поверхностей, определится критерием, предложенным Т. Тальяном:

Здесь R aw – среднее арифметическое отклонение микронеровностей поверхности ролика. В качестве R а 1 принимается среднее арифметическое отклонение микронеровностей поверхности беговой дорожки внутреннего R aв или наружного R aн колец соответственно.

С использованием критерия Л относительная площадь металлического контакт микронеровностей вычисляется по формуле [3] П = 0,25 -Ф ( А )/ 2 •

Здесь Ф ( А ) – интеграл вероятности.

Коэффициент трения в контакте с учетом металлического контакта определим суммой f = f мет П + f см ^{( 1 -} П ⁾ .

Коэффициент трения f мет в контактах микронеровностей принимается по рекомендациям [5].

Коэффициент трения, определяемый сдвигом смазочного слоя, рассчитывается по отношению f .м = W А l/F_m ( i ) .

Здесь W – сила трения, отнесенная к единице длины линии контакта, определяемая по формуле

Выражение для интеграла J имеет вид

J = b m ^{Ф (} х а ^{) ex}P ( O P о ⁾V ^О Р о , где Ф ( х _а ) - интеграл вероятности, в котором предел интегрирования определяется по форму^{ле х} а = 7 ^{2 а} Р о •

При расчётах для контакта с внутренним кольцом принимаем р о = СТ в ( i ) , для контакта с наружным кольцом - р о = СТ н ( i ) .

В формуле для расчёта W знак “+” принимается для поверхности, имеющей большую величину окружной скорости.

В приведенных расчётах вязкость смазки зависят от температуры. В этой связи расчёт коэффициента трения выполняется итерационным методом.

Температура смазки принимается равной температуре соответствующего кольца. Определяются вязкость смазки, толщина смазочного слоя и коэффициент трения. С использованием формулы Блока определяется приращение температуры в зоне трения:

А t = о,83, f ( F m ( i )/ A l )U_S ({^m() x

x(4 AnYncnVn + 4 Aw^A-Vw- У

Здесь Л п и A w - коэффициенты теплопроводности, У п и y _w - плотность, c_n и c_w - удельная теплоемкость материалов колец подшипника и роликов соответственно; V n и V w – скорости поверхностей беговых дорожек колец и роликов; U S скорость скольжения.

Уточнённое значение температуры смазки определяется суммированием tcv = tn + 2 A t/3.

Расчёт повторяется до сходимости с заданной точностью принятого и уточнённого значений температуры смазки.

После уточнений температуры смазки и коэффициента трения определяется сила трения скольжения в контакте

,х Ff = fF(i), где F (i) - нагрузка в контакте ролика с внутренним или наружным кольцом.

При расчете сил трения в контакте торца ролика с направляющим бортиком наружного кольца учитываем, что между торцами ролика и направляющего бортика предусмотрен зазор А б . Величина зазора А б_р в рабочих условиях определяется с учётом температурного расширения.

Принимаем, что между каждым из торцов ролика и гнезда сепаратора устанавливается смазочный слой толщиной h« =А 6р

При вращении ролика касательные напряжения в слое смазки определяются по формуле Ньютона ^ = Д о V s6 !б_б , где V sб – скорость скольжения.

При расчётах вязкость смазки принимаем в зависимости от температуры наружного кольца подшипника.

Скорость скольжения V sб определяем для среднего сечения площадки контакта. При этом, если скорость торца бортика V б больше скорости ролика V wб , то сила трения в контакте является ведущей для ролика, иначе – тормозящей и имеющей отрицательный знак.

Усилие взаимодействия роликов с перемычкой сепаратора определяется суммой

Fs(i)=+ F;, ±Ff ±2Ff,.

Здесь Ffв , Ffн и Ffб силы трения в контактах ролика с внутренним и наружным кольцами и бортиком. Знак “+” выбирается, если скорость поверхности ролика меньше скорости соответствующей поверхности колец в контакте.

С полученным значением усилия взаимодействия определяется напряжение в контакте и полуширина площадки контакта.

Расчёт толщины эластогидродинамического смазочного слоя и силы трения в контакте выполняется как для контакта ролика с кольцом. Приращение температуры в зоне трения определяем при одной не движущейся относительно источника тепловыделения поверхности.

Момент трения между торцами ролика и гнезда сепаратора определяем, принимая, что между каждым из торцов ролика и гнезда сепаратора в рабочих условиях устанавливается смазочный слой толщиной, равный половине зазора между торцами.

При расчётах вязкость смазки принимаем в зависимости от средней температуры подшипника.

Расчёт контакта сепаратора с центрирующей поверхностью бортика наружного кольца выполним как узкого подшипника скольжения [6].

Усилие прижатия сепаратора к центрирующей поверхности определим по формуле

Здесь F cs – центробежная сила при смещении сепаратора.

Составляющие усилия прижатия роликами по координатным осям определяются суммированием проекций усилий взаимодействия роликов с перемычкой сепаратора:

FSB = L (Fs (i)sin(^)- Ffs (i)cos(^));

i = 1

i = 1

Определяются вязкость смазки, толщина смазочного слоя и коэффициент трения при температуре, равной температуре наружного кольца подшипника.

Приращение температуры в зоне трения определяем при одной не движущейся относительно источника тепловыделения поверхности.

После уточнений температуры смазки и коэффициента трения определяется момент трения скольжения сепаратора по центрирующей поверхности.

При расчёте кинематики ролика скорости поверхностей колец (рис.1) в обращенном движении (при остановленном сепараторе) определяются по формулам:

V e = d ep ⁽ H ^{- Ю} в ⁾l² – для внутреннего кольца;

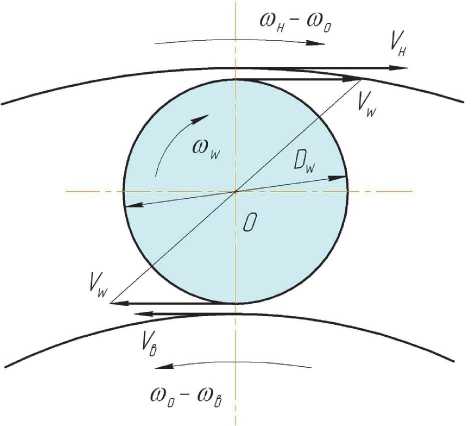
Рис. 1. Схема скоростей поверхностей межвального подшипника

V h = D ,p ( ш. - to o )l 2 – для наружного кольца.

Ведущим в межвальном подшипнике является наружное кольцо. В этой связи поверхность ролика будет иметь проскальзывание некоторой величины относительно кольца. Тогда принимаем V w = V . ( 1 — £ w ) , где £ w - относительная величина проскальзывания ролика в контакте с наружным кольцом. При этом угловая скорость вращения ролика относительно собственной оси будет равна ^H w = ² V w/ D wp .

Скорости скольжения ролика в контактах с кольцами будут равны:

V_se = V w — V_e - для внутреннего кольца;

• V_s . = V . — V w - для наружного кольца.

На рис. 2 приведена схема сил, действующих на ролик в нагруженной зоне.

Здесь F S и F fS – нормальное усилие и сила трения в контакте ролика с перемычкой сепаратора; F с – центробежная сила ролика.

Условие равновесия сил в радиальном направлении определяется выражением

• F . = F e + F fs + F c .

Здесь F в , F н – усилия в контактах ролика с внутренним и наружным кольцами.

В связи с малостью величины силы трения F fS уравнение равновесия в радиальном направлении можно привести к виду

F = F A-F н в c.

Это упрощение позволяет решать задачу о распределении нагрузки по телам качения без учёта сил трения в контактах.

Силы трения F fб и F fS определяются, как показано ранее. Центробежная сила ролика определяется по формуле:

Fc = mw (D.p — Dwp 'ЩЦ2..

Как показано ранее, все силы трения опреде-

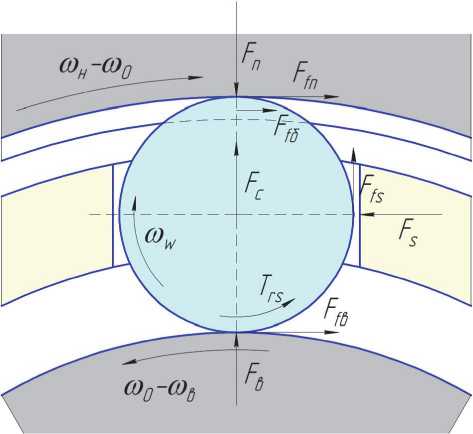
Рис. 2. Схема сил в контактах ролика в нагруженной зоне ляются скоростями скольжения в контактах, которые в свою очередь определяются скоростью вращения ролика относительно собственной оси.

Третьим уравнением равновесия является уравнение моментов

S Т E MFfH - Ffe - Ffs)Dwp /2 + + Ff6 (Dwp - (DHp - D61 V2)- Тsc - Ткн -

• - Т кв - 0 •

Здесь моменты сопротивления качению ролика определим по приближенным зависимостям Т кн ^- f к^FH и Т кв ^{- f}к ^FB - где ^fк ^— коэффициент трения качения.

Разделив на радиус ролика, получим

S Т E w ) - F f_H - F f₆ - F fs +

2 F f ( 1 - ( D h _P - D 6 1 )/ 2 D _wp )

• 2 ( Т sc + Т кн + Т кв )/ D wp - 0. '

Полученное уравнение является функцией одной переменной E . Его решение выполняется итерационным методом Ньютона. При этом производную функции заменяем отношением приращений функции и аргумента.

В результате получаем величину угловой скорости вращения ролика to w и усилие F_s - нагрузки в контакте ролика с перемычкой сепаратора.

Рассматривается также кинематика ролика в не нагруженной зоне.

Таким образом, в межвальном подшипнике все ролики являются “ведущими” по отношению к сепаратору. В то же время в подшипнике с вращающимся внутренним и не вращающимся наружным кольцами ролики в разгруженной зоне являются “тормозящими” и “толкаются” сепаратором. Это объясняет установленное эксперимен- тально небольшое по величине скольжение сепаратора в межвальном подшипнике. Однако при этом наблюдается повышенное скольжение в контактах ролика с кольцами, что может привести к повышенному изнашиванию.

Расчёт сопротивления движению сепаратора в воздушно-масляной среде подшипника выполним по рекомендациям [7].

Температуру воздушно-масляной среды примем равной средней температуре подшипника

t6M = (te + tn )/ 2 .

вм в н

Масло в подшипнике не полностью заполняет весь свободный объем. В этой связи расчётное значение плотности воздушно–масляной среды рекомендуется в зависимости от объемной доли смазки О дсм в полости подшипника по формуле

Г ср = У„о Дсм Кол + 0,6 • О дс,. ) .

Характер движения сепаратора в воздушно-масляной среде определяется числом Рейнольдса, которое в данном случае вычисляется по формуле

Re - Rc tos (v .

Момент сопротивления движению сепаратора в воздушно – масляной среде рекомендуется определять по формуле:

Здесь: R c и r c – радиусы боковой поверхности сепаратора, характеризующего сопротивление вращению его в масляной среде; B s – ширина наружной поверхности сепаратора; C n – коэффициент, зависящий от числа Рейнольдса.

Как показано выше, усилия взаимодействия роликов с перемычками сепаратора являются “ведущими”, обеспечивающими вращение сепаратора. Величина момента сил взаимодействия роликов с перемычками сепаратора определится по формуле i -1

Кроме того “ведущим” для сепаратора межвального подшипник является момент от силы трения сепаратора в контакте с центрирующими поясками вращающегося наружного кольца. Его величина определяется по формуле:

T s6 - fF Rs D s 1 .

Здесь F RS – усилия прижатия сепаратора и f – коэффициент трения в контакте, определяемые, как показано ранее.

Сопротивление вращению сепаратора межвального подшипника будет только от момента трения T ts от перемешивания воздушно-масля-ной среды в полости подшипника.

Величины всех моментов T S , T sб и T RS зависят от угловой скорости вращения сепаратора.

Величину угловой скорости сепаратора в свою очередь можно определить по формуле

• У0 = У00 (1 - £0 ).

Здесь 8 о - коэффициент скольжения а У 00

- теоретическое (при отсутствии скольжения) значение угловой скорости вращения сепарато- ра, величина которого определяется по известной формуле

У00 = (dврЮв + dhp^h V(2(Dp - Dwp )).

Принимаем условие № 0 < ( У н . Тогда с использованием выражений для у и № 00 получим

^£ 0 ^

(ув - Ун )(1 - Dwp /Dpp ) 2У00

Условие равновесия при равномерном вращении сепаратора будет иметь вид:

• ■*0 ) = T s + T s6 - T rs = 0 .

Получено уравнение являющееся функцией одной переменной £ 0 . Его решение выполняется итерационным методом Ньютона. При этом производную функции заменяем отношением приращений функции и аргумента.

В результате получаем величину угловой скорости вращения сепаратора № ₀, величину скольжения £ 0 и усилие и температуры в контактах роликов с кольцами и сепаратором.

Исследование проскальзывания выполним для межвального подшипника 55-2672919Р5 изделия “99В”.

При расчетах скольжения сепаратора принята минимальная радиальная нагрузка F r = 50 Н . Перекос колец принят равным нулю. Скорости вращения колец приняты соответствующими режимам работы подшипника в двигателе.

Температура наружного кольца принята равной 43°С, внутреннего – 47,3°С. Монтажный радиальный зазор в подшипнике принят равным g = 0,043 мм. На рис. 3 и 4 приведены зависимости скольжения сепаратора от разности частот вращения наружного и внутреннего колец (скольжения роторов) при постоянной частоте вращения наружного или внутреннего колец.

При этом постоянная частота вращения наружного кольца (рис. 3) принята равной n н =13067 об/мин , а частота вращения внутреннего кольца (рис. 4) соответственно – n в =8152 об/мин .

Зависимость на рис. 3 показывает, что скольжение сепаратора увеличивается с увеличением скольжения роторов. Эта зависимость монотонная, так как при постоянной частоте вращения наружного кольца с увеличением частоты вращения внутреннего кольца уменьшается не только скольжение роторов, но и рабочее значение радиального зазора вследствие центробежного расширения внутреннего кольца.

Зависимость на рис. 4 не монотонная. При постоянной частоте вращения внутреннего кольца с увеличением частоты вращения наружного кольца увеличивается рабочее значение радиального зазора от центробежного расширения наружного кольца. Вследствие этого уменьшается число роликов в зоне нагружения, что должно привести к отставанию сепаратора, т.е. к увеличению проскальзывания. Одновременно увеличивается скольжение роторов. Для случая, когда скорость вращения наружного кольца больше скорости вращения внутреннего, это может, как показали результаты эксперимента, привести к увеличению скорости вращения сепаратора.

Следовательно, уменьшается скольжение (увеличивается отрицательное значение проскальзывания).

Таким образом, зависимость скольжения сепаратора от частоты вращения наружного кольца имеет сложный характер.

На рис. 5 приведена зависимость скольжения сепаратора от одно-временного увеличения частот вращения внутреннего и наружного колец при постоянной разности скоростей.

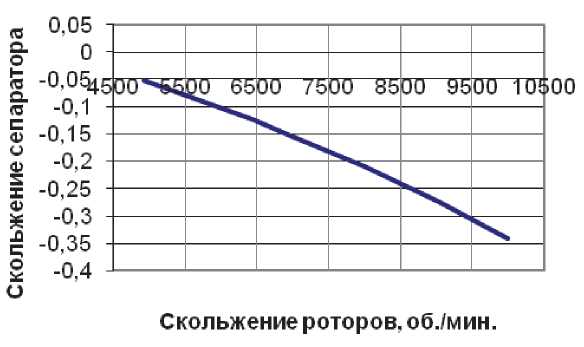
Рис. 3. Зависимость проскальзывания от скольжения роторов при п = 13067 об/мин н

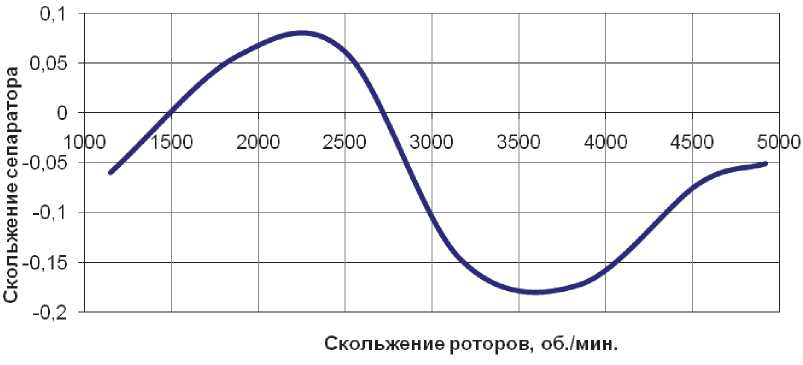
Рис. 4. Зависимость проскальзыванияот скольжения роторов при n =8152 об/мин в

Результаты расчётов показывают, что скольжение сепаратора зависит как от величины скольжения роторов, но и от величин скоростей вращения колец.

На рис. 6 приведена зависимость скольжения сепаратора от радиальной нагрузки при температуре наружного кольца 33 °С и частотах вращения колец: n в =5180 об/мин и п н = 11313 об/ мин . Результаты расчётов показывают известное уменьшение скольжения сепаратора с увеличением радиальной нагрузки на подшипник.

На рис. 7 приведены результаты испытаний подшипника 55-2672919Р5 при различных значениях радиального зазора при смазке маслом ИПМ – 10 [8]. Величины проскальзывания сепаратора приведены в зависимости от частоты вращения наружного кольца. При этом частоты вращения внутреннего кольца соответствовали режимам работы подшипника в изделии.

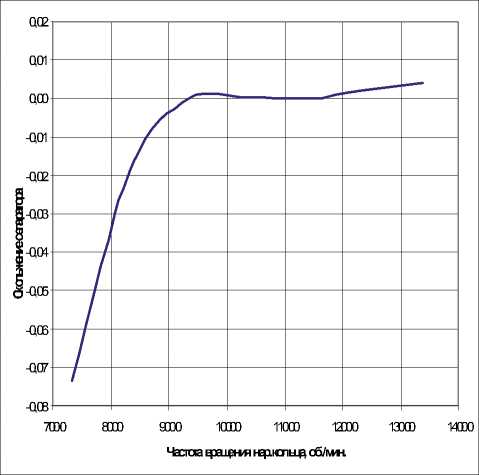
Рис. 5. Зависимость проскальзывания от частоты вращения наружного кольца при П н — П в = 4300 об/мин

Получено уменьшение проскальзывания с выходом оборотов колец на режим полного газа. Это противоречит общепринятым представлениям об увеличении проскальзывания с увеличением частоты вращения подшипника. Однако по нашему мнению в межвальных подшипниках проскальзывание зависит не от абсолютных значений скоростей вращения внутреннего и наружного колец, а от разности их скоростей (от “скольжения роторов”).

Экспериментальные зависимости проскальзывания в подшипнике от разности скоростей вращения колец при нагрузке Fr=50 Н и различных значениях радиального зазора приведены на рис. 8. Видно увеличение проскальзывания с увеличением “скольжения роторов”.

Приведенные результаты экспериментов показали, что на всех режимах испытаний частота вращения сепаратора была выше эпициклической, рассчитанной без учета сил трения в контак-

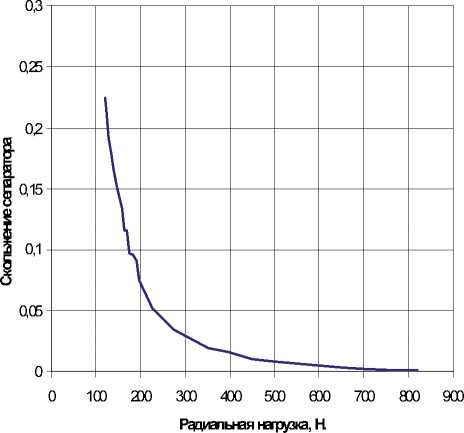
Рис. 6. Зависимость скольжения сепаратора от радиальной нагрузки

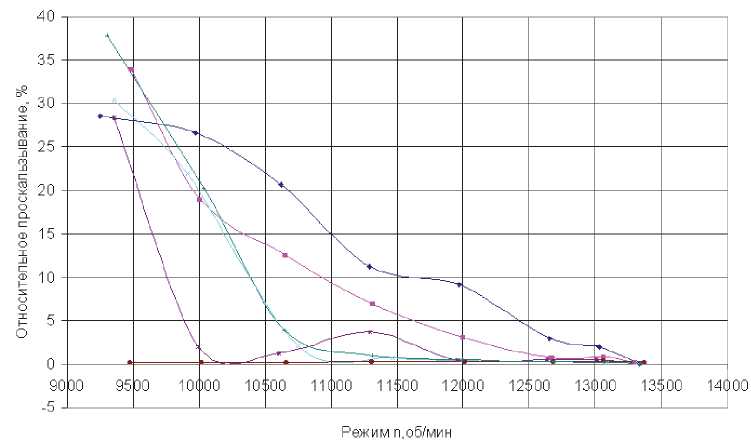
Рис. 7. Зависимость проскальзывания комплекта роликов в подшипнике при F =50 Н от частоты вращения и величины радиального зазора

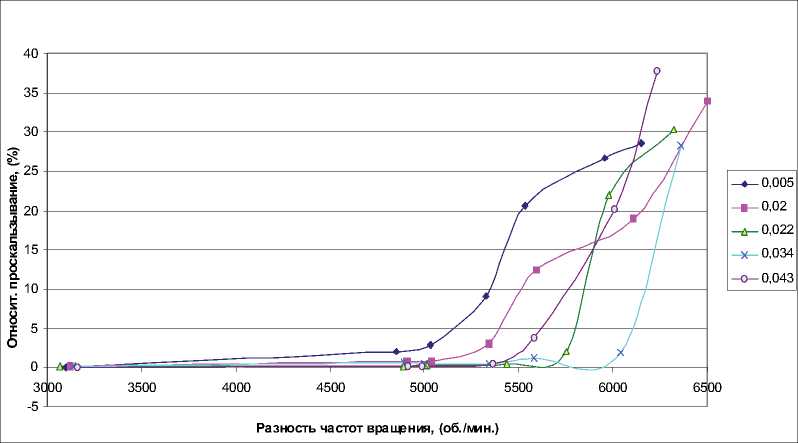
Рис. 8. Зависимость проскальзывания комплекта роликов от разности частот вращения колец при различных значениях радиального зазора

тах и сопротивления вращению сепаратора.

На рис. 9 приведены результаты расчёта проскальзывания сепаратора на режимах испытаний при радиальном зазоре в сборе 0,043 мм и радиальной нагрузке 50 Н .

При выполнении расчётов температуры смазки принимались по экспериментальным данным. Для сравнения там же приведены экспериментальные значения проскальзывания комплекта роликов. Результаты расчётов имеют удовлетворительное соответствие с экспериментальными в связи с многофакторностью зависимости проскальзывания: от радиальной нагрузки, радиального зазора, как от скоростей вращения колец, так и от “сколь жения” роторов, температуры не только наружного, но и внутреннего колец, температуры смазки, ее свойств, объема и способа подачи в подшипник и другое.

К сожалению, многие факторы сложно оценить и учесть в расчётах.

Вместе с тем результаты экспериментов и теоретических расчётов позволяют сделать некоторые выводы о работоспособности межвальных подшипников.

Прежде всего, установлено, что термин “проскальзывание” для межвальных подшипников является условным, так как скорость вращения сепаратора оказывается не ниже, а выше теоретической (эпициклической). Это объясняется тем, что в межвальном подшипнике большинство роликов (даже в разгруженной зоне) являются “ведущими” так как прижимаются значительными по величине центробежными силами к вращающемуся наружному кольцу. Теоретический анализ показывает, что вследствие этого скольжение роликов относительно наружного кольца мини-

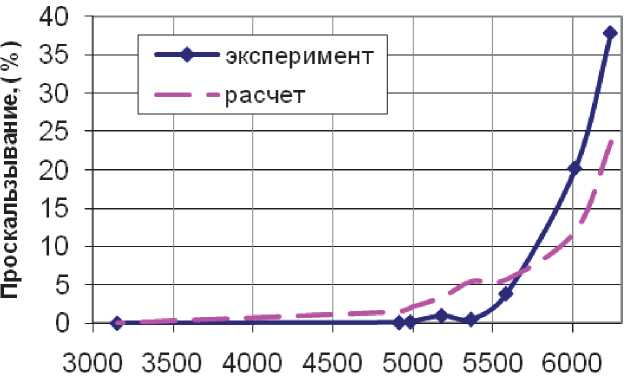
Разность частот вращ.роторов. (об./мин.)

Рис. 9. Зависимость проскальзывания комплекта роликов от разности частот вращения колец при g = 43 мкм и Fr = 50 Н мально и близко к нулю. В то же время наблюдается значительное по величине скольжение роликов относительно внутреннего кольца.

Это говорит о высокой теплонапряженности в контактах роликов с внутренним кольцом и, как следствие, возможности значительного изнашивания и заедания.

Уменьшение скольжения сепаратора и изнашивания на внутреннем кольце может быть обеспечено не только подбором оптимальной величины радиального зазора, но и предварительным нагревом масла, подаваемого в подшипник.