Расчёт собственных функций изображающей двухлинзовой системы в условиях осевой симметрии

В последнее время понятие коммуникационных мод [1, 2] широко изучается и применяется в оптике [3–6]. Вытянутые угловые сфероидальные функции, которые образуют коммуникационные моды для квадратных апертур и преобразования Френеля, также хорошо известны и были изучены аналитически в 1960-х годах [7–9].

Сфероидальные функции представляют собой полный набор функций с ограниченной спектральной полосой, которые ортогональны как на данном конечном интервале, так и на бесконечном интервале [7]. Суперпозиция данных функций, аппроксимирующая некоторое световое распределение, будет обладать инвариантным характером при прохождении через оптические линзовые системы с ограниченной квадратной апертурой [3].

Обобщённые сфероидальные функции [10], тесно связанные с полиномами Цернике, инвариантны к ограниченному преобразованию Ханкеля, они устойчивы к дифракционным эффектам, возникающим из-за ограниченности (круглых) апертур.

В данной работе рассматриваются радиальносимметричные функции, которые при распространении не изменяют свой вид в условиях ограниченных круглой апертуры и спектра самих функций. Подобные исследования проводились для ограниченных квадратных апертур и сфероидальных функций [2]. В работах [11–12] мы продемонстрировали возможность аппроксимации как одномерных, так и двумерных ограниченных сигналов сфероидальными функциями без искажений. В работе [13] рассматриваются сфероидальных моды и обобщённые сфероидальные функции, однако вместо последних при расчёте используются полиномы Цернике.

Заметим, что полиномы Цернике имеют явный аналитический вид и часто используются в задачах адаптивной оптики [14, 15] для расчёта и компенсации искажений волнового фронта. В отличие от базиса Цернике сфероидальные функции не имеют анали- тического представления и вычисляются как собственные функции оператора, связанного с некоторой оптической системой. Разложение по собственным функциям системы позволяет оценить искажение передаваемого сигнала в целом, т. е. оценить качество передачи информации системой.

Нахождение набора собственных функций системы позволяет получить вид сигнала после прохождения через данную систему с помощью аппроксимации по функциям из этого набора.

Теоретические сведения

Предположим, что передняя фокальная плоскость сферической линзы освещается пучком света с распределением f ( x , y ) (оптический сигнал), тогда на задней фокальной плоскости световое распределение будет иметь вид:

+^

F ( u , v ) = j f ( x , y )exp [ - 2 n i ( xu + yv ) ] d x d y .     (1)

-^

Формула (1) представляет собой двумерное преобразование Фурье от исходного оптического сигнала.

Рассмотрим радиально-симметричную функцию:

f ( x , y ) = f (V x ² + y ² ) = f ( r ).                     (2)

Тогда двумерное преобразование Фурье (1) для такой функции будет представлять собой преобразование Ханкеля нулевого порядка [10]:

+^

F ( p ) = H [ f ] ( p ) = 2 n J f ( r ) J о (2 n r p ) r d r ,       (3)

где J_m – функция Бесселя порядка m.

Рассмотрим оптическую установку, изображённую на рис . 1. На круглую апертуру радиуса R падает световой пучок, описываемый радиальносимметричной функцией. Апертура расположена в передней фокальной плоскости линзы. В задней фокальной плоскости линзы располагается ещё одна апертура радиуса P, которая урезает спектр исходной функции. На фокусном расстоянии от вто- рой апертуры расположена аналогичная линза. На расстоянии четырёх фокусов от первой апертуры расположен экран, на котором наблюдается полученное распределение.

Поскольку входная апертура ограничивает распределение падающего светового пучка, для него следует вместо преобразования Ханкеля, интегрирующего по бесконечным пределам, взять ограниченное преобразование Ханкеля, которое зависит от радиуса:

Используя данное свойство для формулы (5), получаем:

тR

H [ f (r )circ - ](p) = H [ f ](p) ** -J1(2nR p).(11)

Rp

Учитываем, что p = uu ² + v ² , и получаем резуль-

тат ограниченного преобразования Ханкеля:

R hR[f!(Р) = 2nJf(r)J0(2кrp)rdr .                (4)

H [ f ( r )] ( p ) ** R J 1 (2 n r p ) = p

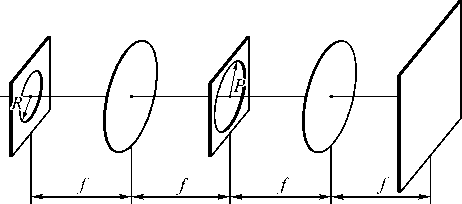
Рис. 1. Схема оптической установки

Ограниченное преобразование Ханкеля с границей R может быть представлено как обыкновенное преобразование Ханкеля от функции, заданной равной нулю за пределами R :

h R [ f ]( p ) = ^H f ( r )circ R ( p ),

где circ ( rIR ) - круговая функция (аналог прямоугольной функции в полярных координатах):

. r    [1, r < R, circ =

R   [ 0, r >  R .

+^ +^

= JJ

-^ -^

RJ 1 ( 2 n Ry] ( u - x )² + ( v - y )² ) 7( u - x )² + ( v - y )²

X H [ f ] (7 x ² + у ² ) d x d y .

X

Именно такое световое распределение придёт на вторую апертуру нашей оптической системы. Вторая апертура урезает полученный спектр, т. е. задаёт его равным нулю за пределами радиуса P . Запишем второе ограниченное преобразование Ханкеля:

h_P H [ f ]( p ) ** RJ 1 (2 n R p ) =

L p J

= H 17 H [ f ]( p ) ** RJ 1 (2 n R p ) I circ p .

LI p               p J

Используя свойство двумерной свёртки, получаем:

H

H [ f ]( p )

**

R _ . _ I . p

J, (2 n R p ) ^circ p ¹ P

rr

= f ( r )circ R ** pJ , (2л; rP ).

( r ) =

Введём в рассмотрение понятие двумерной свёртки функций:

( f ** g )( x , У ) =

+^ +^

= J J f ( u , v ) g ( x - u , y - v ) d u d v =                 (7)

—^ —^

+^ +^

= J J f ( x - u , У - v ) g ( u , v )d u d v .

-^ -^

В случае радиально-симметричной функции двумерная свёртка записывается следующим образом:

2   2   2

r ² = x ² + y y"

^{( f} ** g ^{)( r} ) =

+^ +^   ______

= J J f (7 u ² + v ²) g (7 ( x - u )² + ( У - v )² ) d u d v = (8)

-^ -^

+^ +^

J J f (7 ( x - u )² + ( У - v )² ) g (7 u ² + v²

) d u d v .

-^ -^

Преобразование Ханкеля нулевого порядка обладает свойством, связанным с двумерной свёрткой:

H [ f ** g ] = H [ f ] H [ g ],                        (9)

H [ fg ] = H [ f ] ** H [ g ].                        (10)

Таким образом, мы получили на выходе ту же функцию, что и была на входе оптической системы, с точностью до двумерной свёртки с функцией Бесселя. Более подробно:

h p h R [ f ]( r ) =

... ^pJ 1 ( ^{2 n} P 7 ⁽ x ^- u ^{)2 + (} y ^{- v )2} ) u ² + v ² < R ²       7( x - u )² + ( У - v )²

X f (V u ² + v ²) d u d v .

Формула (15) главным образом отличается от формулы (12) тем, что интегрирование осуществляется по ограниченной области. Похожие соотношения можно встретить в работах [2, 16].

Перейдём в полярные координаты:

x = r cos ф , u = p cos m ,

^Y, ^H        d u d v = p d p d m .       (16)

y = r sin ф , v = p sin m ,

Рассмотрим выражение:

( x — u ) + ( y — v ) =

= ( r cos ф-p cos m )² + ( r sin ф-p sin m )² =        (17)

= p ² - 2 p r cos( m-ф ) + r ².

Выпишем отдельно следующий интеграл:

^lp ^{( r} , Р , Ф ) =

2 п J.

=I -

( 2 п P^ р ² - 2 р r cos( ф-ф ) + r ² )

—- dv.

р ² - 2 р r cos( ф-ф ) + r²

Очевидно, переменная ф пробегает по всему периоду косинуса, поэтому сдвиг на ф можно опустить:

^lp ^{( r} , Р , ^{ф )} = ^lp ^{( r} , р ) =

2п J 1 ( 2nP 7 р ² - 2 р r cos ф+ r ² )                 (19)

= J----, ,          =—" ^d V = ^lp ⁽ р , ^r ).

о д/р - 2 р r cos ф+ r

Таким образом, мы получаем упрощённую запись оператора h_Ph_R :

R hphR[f ](r) = PJLp(r,р)f (р)рdр .                (20)

Множества функций на входной апертуре, на спектральной апертуре и на выходе оптической системы образуют соответствующие гильбертовы пространства. Операторы h R , h P , h P h R являются линейными операторами. Ограничим рассматриваемую область экрана радиусом R (таким образом, гильбертовы пространства на входе и выходе системы будут совпадать) и рассмотрим собственные функции оператора h_Ph_R ( l - номер собственной функции):

h p h_R [ f l ] = Ь i f i .                                      (21)

Скалярное произведение двух радиально-симметричных функций зададим следующим образом:

R

⁽ f , g ) r = J f ^{( r} ) g * ^{( r} ) ^{r d r} ,                       ⁽²²⁾

где R означает, что данное скалярное произведение относится к пространству функций на входе или выходе системы, P - на второй апертуре. Звёздочкой обозначено комплексное сопряжение. Оператор A называется сопряжённым к A , если:

( Af , g ) = ( f , A * g ).                               (23)

Таким образом, оператор h_P h_R является самосопряжённым. Его собственные значения действительны, а собственные функции, соответствующие различным собственным значениям, ортогональны [17].

Функцию распределения светового поля g ( r ) на входе оптической системы можно аппроксимировать собственными функциями:

N

g ^{( r} ) ” Е C n V n ^{( r} ), n = 1

где y n ( r ) - собственные функции, упорядоченные по убыванию собственных значений, C_n - соответствующие коэффициенты разложения, N - заданное число собственных функций. Коэффициенты C n вычисляются как:

C n =

⁽ g , V n ) R ⁽ V n , V n ) R

R

J g ( r ) V n ( r ) r d r

R

J |V n ^{( r ) 2 r d r}

Чем больше будет N , тем точнее получится аппроксимация.

Подставляя вместо оператора A оператор h p h R , получаем:

R

^{( h} P ^h R ^{[ f ]}, g ) R = J ^h P ^h R ^{[ f ](} r ) g * ⁽ r ) r ^d r =

RR

= J ^P J L P ^{( r} ’ р ) ^{f (} р ) р ^d Р g * ^{( r} ) ^{r d r} =

0 L 0

RR

= P J J L p ( r , р ) f ( р ) g * ( r ) r р d р d r = 00

R      Г R

= J f ( р ) P J L p ( р , r ) g ( r ) r d r

0         L 0

р d р =

R

= J ^{f (} р ) { ^h P ^h R ^[ g ^] }’ Ф) р ^d Р = ^{( f} , ^h P ^h R ^[ g ^]) R .

Численный расчёт

Решение задачи на нахождение собственных значений и собственных функций оператора h P h R будем искать численно, решая аналогичную задачу линейной алгебры для дискретного аналога заданного оператора. Радиус первой апертуры R в расчётах всегда принимаем равным единице. Радиус второй апертуры (спектра) P будем варьировать, от него зависит число степеней свободы нашей системы.

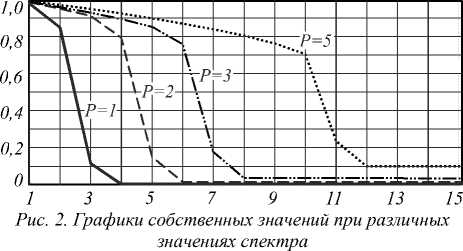
На рис. 2 изображены графики собственных значений при различных параметрах спектра. Можно увидеть, что количество значащих собственных чисел увеличивается с увеличением спектра системы. Начиная с некоторого номера, все собственные значения приближённо равны нулю. Из рисунка может показаться, что это не так, в частности, при P = 5 начиная с 12-го собственного значения соответствующий график прекращает убывать и остаётся на отметке 0,1. Однако увеличение числа отсчётов дискретизации устраняет данную ошибку вычислений. Похожее «ступенчатое» поведение имеют собственные значения сфероидальных функций, являющихся собственными к ограниченному преобразованию Фурье [8].

На рис. 3 показаны примеры собственных функций системы при значении спектра P = 3.

Из рис. 2 видно, что ширина спектра P определяет число значащих собственных значений оператора распространения. Проведём аппроксимацию светового поля, используя формулу (26). На рис. 4 представлено приближение собственными функциями круговой функции. Она принимает значение 1 при r ≤ 0,5, а за пределами данного множества – значение 0. Ширину спектра P принимает равным трём. Аппроксимация осуществляется тремя, пятью и семью функциями. Дальнейшее увеличение числа N не приносит значительных изменений, поскольку значащих собственных значений семь. График на рис. 2 для P = 3 показывает, что все собственные значения очень близки к нулю, начиная с восьмого. Среднеквадратическое отклонение при N =7 составляет 19 % (рис. 4).

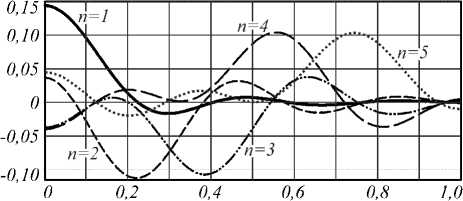
Рис. 3. Пять примеров радиального сечения собственных функций для фиксированного значения спектра

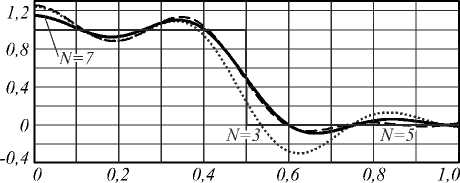
Рис. 4. Аппроксимация круга собственными функциями (радиальное сечение)

Двумерные представления круговой функции и её аппроксимации семью собственными функциями изображены на рис. 5 а , б .

Рис. 5. Круговая функция (а) и её аппроксимация (б)

б)

Другой пример входного поля – кольцевая функция. Она принимает значение 1 внутри отрезка 0,25 ≤ r ≤ 0,5 и значение 0 – за его пределами. Полученные графики можно увидеть на рис. 6. Соответствующее двумерное представление показано на рис. 7 а , б . Среднеквадратическое отклонение составляет 31 %.

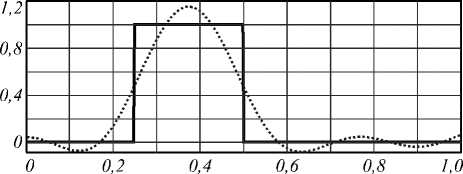
Рис. 6. Аппроксимация кольца собственными функциями (радиальное сечение)

Рис. 7. Кольцевая функция (а) и её аппроксимация (б)

б)

Рассмотрим в качестве примера непрерывную функцию:

g ( r ) = exp

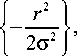
где σ = 0,12. Её аппроксимация семью собственными функциями показана на рис. 8. Двумерное представление изображено на рис. 9 а , б . Среднеквадратическое отклонение не превышает 5 %.

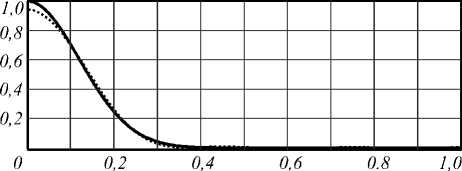
Рис. 8. Аппроксимация экспоненциальной функции собственными функциями

а)

б)

Рис. 9. Экспоненциальная функция (а) и её аппроксимация (б)

Заключение

Мы рассмотрели оптическую установку, состоящую из двух линз и двух ограниченных круговых апертур (рис. 1), и нашли собственные функции системы (рис. 3), согласованной с этой установкой. С помощью численных расчётов мы установили, что ширина спектра (радиус второй апертуры установки) прямо пропорциональна числу степеней свободы системы. Для аппроксимации светового поля можно ис- пользовать собственные функции, соответствующие собственные значения которых не равны (приближённо) нулю (рис. 2). Чем шире спектр, тем таких функций больше и, следовательно, погрешность аппроксимации меньше.

В качестве примера мы рассмотрели три радиально-симметричные функции: круговую (рис. 4, 5 а , б ), кольцевую (рис. 6, 7 а , б ) и экспоненциальную (рис. 8, 9 a , б ). Радиусы апертур при этом были зафиксированы. В отличие от кольцевого и кругового сигналов, содержащих высокочастотные составляющие, наилучшего приближения собственными функциями удалось достичь для случая экспоненциального пучка, который не содержит составляющих с высокими частотами: среднеквадратическое отклонение составило всего 5 %. При этом для обеспечения такой низкой ошибки аппроксимации требуется небольшое число собственных функций.

Работа выполнена при поддержке Министерства образования и науки РФ и гранта РФФИ 13-07-00266.