Расчёт собственных волн планарного анизотропного волновода для различных положений оптической оси

В настоящее время происходит интенсивное развитие технологий оптоэлектроники и интегральной оптики, значительно вырос интерес исследователей к волноведущим оптическим структурам [1]. Это можно объяснить развитием оптических технологий обработки и передачи информации, разработкой фотонных интегральных схем, оптической памяти [17]. Преимуществами оптических волноведущих структур являются высокая скорость передачи информации, низкая стоимость сырья, компактные размеры. Планарные диэлектрические волноводы являются важнейшими элементами новых высокоскоростных технологий. Толщина волновода и его оптические параметры определяют особенности распространения и отражения в нём электромагнитных волн, то есть его собственные моды. Известно, что в анизотропных средах электромагнитные волны распространяются иначе, чем в изотропных средах [2]. В анизотропной среде оптические свойства зависят от направления распространения света, и поэтому ориентация оптической оси волновода должна влиять на условия распространения собственных волн. Новые оптические решения требуют создания сред со специальными оптическими свойствами. Как известно, интегрально-оптические компоненты изготавливаются в очень сложных технологических процессах, например, в процессе ионной имплантации. Чтобы создаваемые устройства функционировали так, как это планирует разработчик, необходим детальный анализ волноводных характеристик распространения, а также разработка простого набора расчётных инструментов для производства. Для этого требуется адекватная математическая модель взаимодействия электромагнитных волн с веществом, построенная на уравнениях Максвелла.

За последние десятилетия разработано множество аналитических и численных методов расчёта волноводных мод [3–4]. Метод распространения луча применён в работе [7] для анизотропного тонкого волновода. Рассматривалась трёхслойная система. В случае произвольной ориентации оптической оси анизотропного волновода в каждом слое будет происходить кросс-поляризация, взаимодействие волн. Для описания этого явления в работе [8] Юхом была предложена новая 4×4 матричная алгебра, которая комбинирует метод матриц 2×2 и метод матриц Джонса. Она была применена для исследования распространения плоской волны в произвольной анизотропной среде. Для каждого слоя записывалась матрица распространения; было выяснено, что вид матрицы зависит от ориентации оптического тензора относительно осей волновода. Процедура, основанная на формализме матриц Юха 4×4, получила развитие в работе [9]. Было найдено асимптотическое решение для набора очень тонких слоёв, толщиной значительно меньше длины волны. Метод подбора нулевых элементов характеристической матрицы был предложен в статье [10]. Его применяли для многослойного планарного оптического волновода с заданным профилем показателя преломления. Постоянные распространения волновода были получены из условий равенства нулю элементов передаточной матрицы. Метод применялся к волноводам с потерями и анизотропией. В работе [11] был предложен метод передаточной матрицы. Это стандартный матричный метод 2×2, используемый для оптики тонких плёнок. Его применили к планарному многослойному волноводу. Получены выражения для расчёта профилей полей и энергии в каждом слое. Метод, применённый к поглощающему многослойному волноводу и к отражению плоской волны, был предложен в [12]; он является адаптированной для планарного волновода модификацией метода характеристических матриц [2]. В монографии [1] предложен детальный теоретический анализ различных видов оптических волноводов. Детально исследованы условия существования волн, получены дисперсионные уравнения для расчёта зависимости показателя преломления для первых двух мод от относительной толщины волновода, указан интервал для верхнего предела «изменения показателя преломления».

Для расчёта и анализа волноводных мод часто применяют модификации метода конечных разностей для временной и частотной области, а также метод конечных элементов. Оригинальный алгоритм был предложен Йи [13]. Новая полно-векторная конечно- разностная дискретизация для волноводов с поперечной анизотропией была предложена в [14]. В отличие от предшествующих решений метод позволяет решать задачи для произвольной ориентации оптической оси относительно распространения волны. Метод конечных элементов применялся для расчёта мод при различных углах распространения в работах японских учёных [15] и [16]. Численные методы позволяют выполнить решения для собственных мод для волноводов с различными оптическими свойствами и геометрией. Однако их общими недостатками являются появление нефизических зависимостей, а также затруднённость в анализе решения.

1. Постановка задачи

жённостей электрического и магнитного полей для неё имеют вид:

E TE = ( 0 E y 0 ) ,                              (2а)

H TE = ( H y 0 H z ) .                        (2б)

Вторая волна в кристалле «2» является необыкновенной, это TM-волна. Вектор напряжённости электрического поля для данной волны лежит в плоскости падения и имеет компоненты E X , E z , а

вектор H перпендикулярен ей, поэтому имеет только компоненту H y :

^ETM =^{( E}x ^{0 E}z ) .                             ^{(3 а )}

H TM = ( 0 H y 0 ) .                         (36)

В настоящей работе, исходя из уравнений классической электродинамики, выполнена сшивка решений на границах трёхслойного однородного волновода с внутренней анизотропной средой с помощью матрицы Коши. Выполнен расчёт решений дисперсионных уравнений для волн TE и TM, распространяющихся в анизотропном волноводе, получена зависимость асимптотики дисперсионных кривых от угла наклона оптической оси волновода.

Рассмотрим распространение электромагнитной волны в анизотропном плоском слое. Он представлен на рис. 1. Покровная среда «1» и подложка «3» имеют меньшие значения диэлектрической проницаемости, чем значения ε О , ε e второй среды, и обеспечивают распространение электромагнитной волны в пределах слоя «2» в плоскости X0Z за счёт явления полного внутреннего отражения. Плоскость распространения волн X0Z, показанную на рисунке, будем называть плоскостью падения. Пусть оптическая ось анизотропной среды волновода ориентирована в плоскости падения под некоторым углом φ к оси OX.

Подставим векторы (2) и (3) в уравнения Максвелла и учтём, что для всех компонент полей F i

выполняются условия:

—Fi = 0 d y ¹      ’

l"F i = k 0 0 « F . d z

(4а)

(4б)

Параметр а зависит от угла падения волны на границы раздела x = 0 и x = d и от оптических свойств волновода. Значения углов падения 6 1 , 6 ₃ в средах «1» и «3», а также значения углов 6 _TE и 6 _TM в слое «2» связаны с оптическими свойствами мате-

риалов законом Снеллиуса:

а = ^ 8 1 Ц 1 sin 6 1 = 8 ₃ Ц ₃ sin 6 ₃ =

⁸ yy Ц sin ⁶ TE

= n e

^{sin 6} TM

= const.

Здесь n e = ^ 8 _o cos²( 6 — ф ) + 8 _e sin² ( 6 — ф ) - показатель преломления для волны TM в слое «2» [2, с. 627].

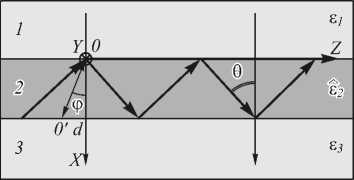
Рис. 1. Однородный анизотропный планарный волновод. 00’ – оптическая ось анизотропной среды «2» расположена в плоскости XOZ под углом φ к оси OX

При указанном положении оптической оси ди-

электрическая проницаемость одноосной анизотроп-

ной среды «2» имеет вид: (

8 _e cos² ф + 8 „ sin² ф

£ 2 =

к

⁸ o

8 J дт2ф

. (1)

£ — 8

e 2 ° sin2 ф

⁸ o

cos² ф + 8 _e sin² ф

Рассмотрим распространение в среде «2» волн двух типов. Первая волна будет обыкновенной волной в кристалле «2»; это TE-волна. Векторы напря-

2. Решение уравнений Максвелла

Подстановка векторов (2) и (3) в уравнения Максвелла с учётом связей (4) и (5) позволяет получить две системы, состоящие из двух обыкновенных дифференциальных уравнений. Первая система ОДУ описывает распространение в среде «2» TE-волны:

d XE y = ik„Н ,

К k 2k                       (6)

• -d H z = ik 0 f 8 yy — — 1 E y .

• d x         к yy Ц 7 y

Вторая система из двух ОДУ отвечает за распространение в среде «2» волны TM:

A H y, = — ik 0 a^ x H y — ik 0 f8 _zz —^ x A x 1 d x y 0 8 y 0 zz 8

zz                              xx d Z7 f (    a2 A. ., 8xz

— ^Ez =^— Ik 0 I ^Ц     I ^H y ^— Ik 0^a-- ^E z .

_ d x            к    8 xx 7 y 8 xx

E z ,

Для решения систем ОДУ (6) и (7) были найдены фундаментальные матрицы решения, а затем получены матрицы Коши для TE- и TM-волн в анизотропном слое. Данный метод применялся в работах

5, 6, 18]. В работах [19, 20] были получены матричные решения для однородного анизотропного слоя. «Сшивка» решений на границах «1 –2», когда x =0, и «2–3», когда x = d , для компонент полей TE-волны

Из формул (10) и (11) следует, что связь между компонентами H и E имеет вид:

yz

имеет вид:

f E y ( d ) ) I H ( d ) J

( TE ) ( TE ) n ₁₁ n ₁₂

H y =±    ^∆ E z .

ε _xx µ - α ²

( ^TE ) ( TE )

V n 21 n 22

J

f E y (0) ) V H z (0) J ^.

Угол падения электромагнитной волны TM в слое «2» равен θ _TM . Если E _TM – вектор напряжён-

Коэффициенты матрицы Коши в уравнении (8) имеют вид:

ности электрического поля, то E TM cos θ TM – его проекция на ось 0Z. Теперь нам известны тангенциаль-

n ₁ ⁽ ₁ ^{TE )} = n ₂ ^{( T} ₂ ^{E )} = cos( k ₀ d ε _yy µ-α ² ) ,

(8а)

( TE ) n 12 ⁼

i µ

-

sin( k ₀ d ε _yy µ-α ² ) , α ²

(8б)

ные составляющие вектора H для падающей и отражённой в олн:

H_y = ±           E_TM cos θ _TM .             (13)

ε _xx µ - α ²

_{( TE )} i ε _yy µ - α n 21   ⁼

µ

sin( k ₀ d ε _yy µ-α ² ) .

(8в)

Матричная «сшивка» решения для TM-волны на границах слоя «2» записывается в виде:

' H y ( d ) V n (™ ) n TM ) E z ( d ) J V n 2 TM ) n 2²2²⁾

⋅

H y (0)

E z (0)

.

«Сшивка» граничных условий на плоскости x = 0

для волны, распространяющейся из среды «2» в среду

«1» и отражённой в слой «2», позволяет получить ам-

плитудный коэффициент отражения для TM-волны:

R p

ε ₁ ( ε _xx µ- α ² ) - ∆ cos θ ₁ ε ₁ ( ε _xx µ - α ² ) + ∆ cos θ ₁

Матрица Коши N ˆ _p ( d ,0) в формуле (8) для ны TM имеет вид:

вол-

В слое «2» будет происходить полное внутреннее отражение при углах θ TM , больших угла ~ θ , оп-

n ₁ ( ₁ TM ) ₌ n ₂ ( T ₂ M ) ₌ e

- ik ₀ α d ^{ε xz}

^{0 ε} xx

, , V ^{A ( e} xx Ц ^-а 2 )' cos k 0 ^d--------------

ределяемого по формуле:

V

ε xx

J

( TM ) n 12    ⁼

= ie

ε

- ik ₀ α d ^xz

ε _xx

4 _       -2

ε _xx µ - α ²

( TM ) n ₂₁

,

(9а)

θ = arcsin

_V VE „ sin² ( 6 - Ф ) + ^e e cos² ( 6 - Ф ) x

. , J ^{A ( e} xx Ц ^-а ) , sin k о (P------------

ε

- ik 0 α d ^xz ε _µ-α 2

= ie ^{xx xx}

∆

f

- sin k 0 d

V

ε xx

xx

^{A ( E} xx Ц^-^) '

ε xx

.

J

(9б)

(9в)

Величина ∆ = ε ε - ε ε = ε ε не зависит от xx zz xz zx o e

ориентации оптической оси в плоскости X0Z. Формулы (8) и (9) позволяют рассчитывать локализацию полей электромагнитной волны в волноводе. Из формул (9а) – (9в) видно, что собственные значения системы ОДУ (5) принимают значения:

λ 12 =± i k 0 ^{∆ ( ε xx µ - α 2 )} - i α k 0 ^{ε xz} .         (10)

, xx                   xx

Второе слагаемое в формуле (9) объясняет появление фазового множителя в коэффициентах матрицы (9). Сшивки (8) и (9) получены путём решения систем ОДУ при помощи матрицанта. Как правило, при расчётах применяют метод передаточной матрицы [11], в котором фазовый множитель опускают. Исходя из уравнений Максвелла, связь между компонентами напряжённости электрического и магнитного полей TM-волны записы-

вается в виде системы:

f ^k z H y = ^k 0 ⁽E xx^Ex +E xz E z ) ,

1 k x^Hy =- ^k 0 ⁽e zx^Ex + e zz^Ez ) .

Исходя из формулы (14), по методу, показанному в работе [2, с. 65], получим выражение для сдвига фазы при отражении от границы «2– 1»:

f A $ 2, -- larCtg^--. V ’

α 2 -ε 1 e xx Ц - а

Аналогичная формула справедлива для границы «2–3».

f 8 23 = - 2arctg V e 3    v

α 2 -ε 3 ε µ-α 2 xx

3. Решение дисперсионных уравнений

Величина ∆ при любом значении угла ϕ остаётся неизменной, а значение ε xx является функцией этого

угла.

Для того чтобы волна могла распространяться в волноводе, необходимо, чтобы при её распространении от границы «1 –2» к границе «2–3», с учётом сдвига фаз при отражении, от покровной среды и от подложки изменение фазы было кратно π . Это усло-

вие определяет вид дисперсионного уравнения для

мод TM планарного волновода:

k ₀d ∆ ( ε xx µ-α ²) ε xx

- arctg

a

El

V ¹

α ² -ε ₁

ε µ-α ²

xx

- arctg

∆ α - ε ₃

V ^E 3   ^E xx Ц^-а

= m π , m ∈ N .

Уравнение, аналогичное (18), было получено в работе [12], однако в этой работе задача решалась для диагонального тензора ε 2 . Величина εxx несёт информацию об угле ϕ. Следовательно, несмотря на универсальный характер уравнения (18), его решения для анизотропного волновода должны определяться положением оптической оси.

Дисперсионное уравнение для TE-волны будет совпадать с дисперсионным уравнением TE-волн в изотропной среде с диэлектрической проницаемо- стью ε2 = εyy : k0d εyyµ2 - α2 - arctg

„ | а2-е3ц3 | _

α ² - ε ₁ µ ₁ ε _yy µ ₂ - α ²

- arctgl ------- 3-3- I = п m .

l\ ^E yy ^ 2 ^-а J

Между параметром α и постоянной распространения β существует связь: β = k 0 α . На рис. 2 представлены дисперсионные кривые для волны TE для мод m =0, 1, 2, 3, 4, являющиеся решениями уравнения (19). Случай распространения TE-волны в анизотропной среде при заданной выше ориентации оптической оси аналогичен распространению волны

TE типа в изотропной среде, как это и следует из

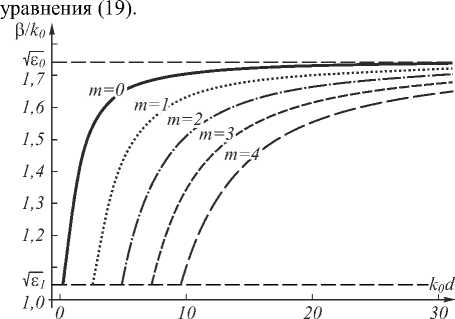
Рис. 2. Зависимость постоянной распространения β от фазы k0d волны TE в анизотропном планарном волноводе для мод TE0 – TE4

Решение уравнения (18) для TM-волн выполнялось численно для искусственной среды с параметрами тензора диэлектрической проницаемости ε _O =3, ε _e =4. Значения угла φ между оптической осью кристалла и нормалью, проведённой к границам раздела сред (рис. 1), изменялись в пределах [0°; 90°].

Расчёт показал, что для TM-волны положение дисперсионных кривых зависит от угла φ. Горизонтальная асимптота y = A ограничивает графики, составленные из точек, являющихся решениями дисперсионного уравнения, сверху. Значение A зависит от угла φ и связано с показателем преломления необыкновенной волны. Если угол ϕ = 0, высота горизонтальной линии будет равна величине: A = ε _e . Графики, рассчитанные при значении угла ϕ = 0, когда оптическая ось совпадает с осью OX, представлены на рис. 3 а .

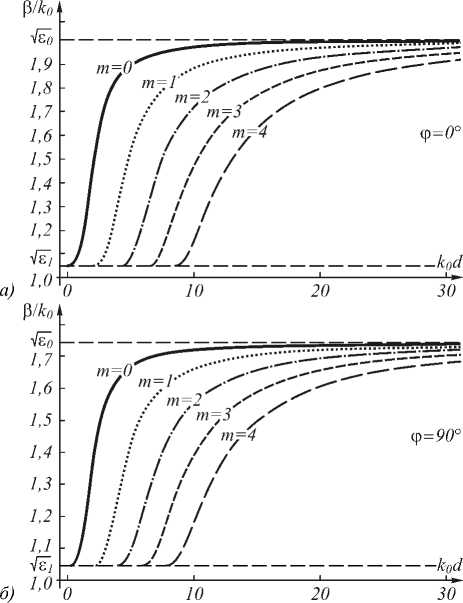
Рис. 3. Зависимость постоянной β от фазы k₀d в анизотропном планарном волноводе для мод TM₀ – TM₄: угол φ = 0° (а), угол φ = 90° (б)

Параметр A в этом случае будет максимально отличаться от асимптоты графиков TE-волны, приведённых на рис. 2. Если угол ϕ = 90 ° , положение асимптоты будет таким же, как и в изотропном случае: A = ε _o (рис. 3 б ). Это не противоречит результатам, представленным в монографии [1]. Из них следует, что верхний предел изменения параметра n B , равного α , «заключён в интервале между n ₁ и n ₃», иными словами, между

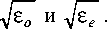
Для произвольного значения угла φ параметр A принимает значение, равное показателю преломления необыкновенной волны для максимально возможного угла (90 ° – ϕ ), между волновым вектором и оптической осью:

A = ε _o sin ² ϕ + ε _e cos ² ϕ . (20)

Если угол наклона оси OO’ равен ϕ , а волна распространяется вдоль оси OZ, что соответствует максимальному значению α , то угол между волновым вектором и оптической осью будет равен (90 ° – ϕ ).

На рис. 4 а , б представлены дисперсионные кривые для случаев, когда угол ϕ составляет 30° и 60°. Нижняя штриховая линия на рис. 2–4 соответствует наименьшему значению параметра α при угле полного внутреннего отражения ~ θ : α _min = max( ε ₁, ε ₃) . При изменении в формуле (1) для тензора диэлектрической проницаемости среды «2» угла φ на «–φ» характер зависимостей не изменяется.

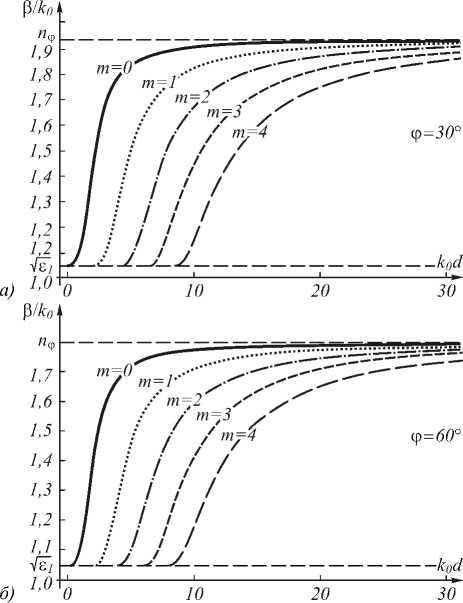
Рис. 4. Зависимость постоянной распространения волны TM в анизотропном волноводе для мод TM0 – TM4 от фазы k0d при различных значениях угла φ: φ = 30° (а), φ = 60° (б)

Заключение

В данной работе была получена математическая модель для расчёта собственных мод планарного анизотропного волновода для произвольного наклона оптической оси в плоскости падения. Исследована асимптотика дисперсионных кривых для TM-волны в зависимости от угла ориентации оптической оси в плоскости распространения волны.