Расчёт спектральной линзы для получения нормализованного вегетационного индекса

В настоящий период наблюдается значительный рост рынка данных дистанционного зондирования Земли, а также активное совершенствование методов обработки и классификации данных [1 – 4], что в свою очередь обуславливает перспективность данного направления в решении разнообразных задач потребителей информации. Параллельно происходит интенсивное развитие беспилотных авиационных систем (БАС) [5] и средств мониторинга, интегрируемых с ними [6]. Особый интерес представляют мульти- и гиперспектральные системы, которые обладают высоким потенциалом применения, например в интеллектуальных системах управления сельским хозяйством [7 – 9] за счет возможности получения данных в большом числе спектральных каналов. Наряду с развитием БАС наблюдается тенденция к снижению массогабаритных характеристик систем мониторинга. В контексте конкретных агротехнических задач важной становится разработка компактных и легких специализированных систем мониторинга, способных обеспечивать регистрацию данных по информативным спектральным каналам [10, 11]. Данные спектральные каналы применяются для расчёта вегетационных индексов, которые в свою очередь могут использоваться в качестве входного признака index. Computer Optics 2025; 49(6): 961-971.

регрессионной модели, используемой для решения множества задач управления сельских хозяйством: оценка и прогнозирование урожайности [12 – 14]; определение содержания хлорофилла, азота, воды [15 – 17]; определение и картирование заражений [18 – 20] и др. Для вычисления вегетационных индексов обычно используются относительно узкие спектральные каналы. В оптическом диапазоне электромагнитного спектра под относительно узким спектральным каналом обычно понимается интервал спектральной выборки (приходящийся на пиксель регистратора) не более 10 нм, под относительно широким – интервал спектральной выборки шириной в десятки или сотни нанометров [21].

Различают множество подходов к разделению светового потока в узкие спектральные каналы, которые реализуются в миниатюрных спектрометрах, это: дисперсионный, фильтрующий, на основе преобразования Фурье. Дисперсионные оптические схемы миниатюрных спектрометров могут использовать: отражающую плоскую [22] или вогнутую [23] дифракционные решётки; сочетание в одном элементе линзы Френеля и дифракционной решётки [24]; различные волноводные схемы в сочетании c дифракционной решёткой внутри [25, 26], фотонным кристаллом [27], цифровой планарной голограммой [28], решёткой эшелле [29], а также схемы основанные на волноводной решётке [30]. В свою очередь, миниатюрные спектрометры на основе узкополосных фильтров могут быть реализованы с использованием: настраиваемых акустооптических [31], жидкокристаллических [32] фильтров, фильтров Фабри-Перо [33]; массивов фильтров Фабри-Перо [34], основанных на тонких плёнках [35], фотонных кристаллах [36], метаповерхностях [37]; линейно переменных фильтров клиновидных [38] или градиентных [39]. Миниатюрные Фурье спектрометры обычно основаны на интерферометрах Майкельсона [40], Маха-Цендера [41] и т.д. Приведённые выше спектрометры, позволяют получать информацию в десятках – сотнях узких спектральных каналов, при этом, как уже было отмечено ранее, для решения конкретных задач, наличие такого множества спектральных каналов является избыточным. При этом имеются технологические ограничения при изготовлении многих компонент (например, узкополосных фильтров, тонких плёнок и т.п.).

Если рассмотреть изображающие мультиспектральные датчики, то для получения изображения в нескольких спектральных каналах традиционно используются фотоприёмные матрицы c цветными фильтрами типа Байера или альтернативными, например [42]. В работе [43] вместо цветных фильтров используется матрица дифракционных фильтров. В работе [44] рассматривается оптическая система, состоящая из ДОЭ и матрицы цветных светофильтров, устанавливаемых вблизи фотоприёмной матрицы. Особенностью спектральных или дифракционных фильтров для вышеприведённых систем является пропускание в относительно широком интервале длин волн оптического диапазона электромагнитного спектра. Однако использование ДОЭ [44] в схеме с таким фильтром позволяет формировать изображение в гармониках т.е. узких спектральных каналах. Другой стратегией спектрального разделения может быть сочетание рефракционно-дифракционных оптических систем с кодированной апертурой [45], а также, например, рассмотренных выше, узкополосных фильтров [35, 38]. Таким образом, в таких датчиках для спектрального разделения светового потока и формирования изображения необходимо использование как минимум двух элементов, оптического и фильтрующего световой поток.

Интересной представляется разработка конструктивно более простых и недорогих в изготовлении оптических систем, которые реализуют получение изображения в выбранных спектральных каналах без использования дополнительных светофильтров. Метод расчёта подобной системы – спектральной дифракционной линзы (СДЛ) рассмотрен в работе [46]. Такой СДЛ реализует спектральное разделение светового потока для выбранных длин волн и формирование оптического изображения на монохромном фотоприёмнике. В работах [47 – 49] рассматривается изготовление СДЛ для решения различных прикладных задач. Рассматриваемые СДЛ формируют изображение в спектрах ±1 порядка дифракции, при этом используется коллимирующая оптическая система, устанавливаемая непосредственно перед СДЛ [47].

В отличие от [24, 46 – 49] в настоящей работе предлагается исследовать возможность использования обыкновенной собирающей линзы в качестве элемента, формирующего оптическое изображение в узких спектральных каналах. Настоящая статья состоит из нескольких разделов. В первом разделе рассматривается концепция такой линзы, а также выбираются её конструктивные параметры. Во втором – представлен математический аппарат, использованный для расчёта кодированной апертуры на входной плоскости перед линзой. В третьем и четвёртом разделах проводится вычислительный эксперимент по расчёту фазовых и эйкональной функции на входной плоскости линзы и оцениваются передаточные характеристики полученной модели линзы. Анализ полученных результатов проводится в пятом разделе.

1.    Постановка задачи

В качестве стратегии спектрального разделения светового потока линзой было выбрано применение пропускающей дифракционной решётки, аналогично [24, 46]. Было принято, аналогично [46], что решётка нанесена на вторую поверхности линзы. В предметной области такой линзы располагается апертурная диафрагма (или щель) и при этом линза должна формировать изображение апертурной диафрагмы в узких спектральных каналах без использования дополнительных коллимирующих элементов. Известно, что при нахождении предмета на расстоянии а = 2f от собирающей линзы получается действительное, зеркально перевёрнутое и равное по величине предмету изображение на расстоянии а' = 2f . Поэтому данная концепция была выбрана при расчёте параметров такой линзы. Также было выбрано что суммарное расстояние от предметной до изображающей плоскостей должно быть менее 100 мм, при этом спектральное разделение должно происходить в диапазоне от 600 до 800 нм, где находится большое число узкополосных вегетационных индексов [12 – 20].

Расчёт параметров поверхностей проводилась с использованием инструментов трассировки и локальной оптимизации Zemax c применением оценочной функции RMS – Spot Radius. Точечные диаграммы (или пятна рассеяния) относительно минимальных размеров (радиус несколько десятков микрометров) по полосе захвата линзы были получены в спектре первого порядка только на одной длине волны, тогда как на других длинах волн, радиусы пятен составляли сотни микрометров в результате чего происходило их значительное взаимное перекрытие. С учётом этого проводился подбор параметров при условии того, что размеры пятен рассеяния должны быть приблизительно одинаковыми в рассматриваемых диапазонах изменения спектральных и пространственных координат. В результате такой оптимизации линзы в Zemax для трёх длин волн 600 нм, 700 нм, 800 нм в спектре первого порядка для областей в центре и на краях поля зрения (0,1 мм, –1 мм) были получены параметры линзы (рис. 1), у которой первая поверхность (по ходу распространения светового пучка) является чётной асферикой, а вторая сферической с дифракционной решёткой, имеющей частоту штрихов 50 лин/мм. Радиус кривизны первой поверхности Rr = 21 мм (параметры чётной асферики а = 18,100, а2 = -1,041 * 10s, а3 = 6,907 х 10 7), второй - R2 = -22 мм. Толщина линзы составила 3 мм, диаметр 11 мм, а общее расстояние от предметной плоскости до плоскости изображения – 63 мм.

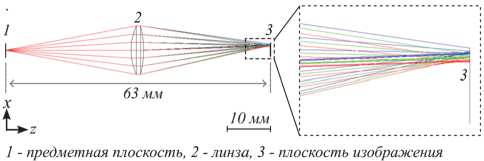
Рис. 1. Ход лучей в Zemax (меридиональное сечение) для трёх длин волн 600 нм, 700 нм, 800 нм (красный, зелёный и синий цвета) и увеличенное изображение пересечения лучей плоскости изображения в спектре первого порядка

На рис. 2 показаны точечные диаграммы (точки пересечения лучей плоскости изображения), полученные в Zemax для трёх длин волн в спектре первого порядка.

Из рис. 2 видно, что точечные диаграммы имеют достаточно большой радиус, что не предполагает регистрацию спектра в узких спектральных каналах, а также использование линзы в качестве изображающей системы. Устранение данных ограничений возможно при использовании концепции кодированной апертуры, аналогично работе [45]. Для получения корректных результатов, на начальном этапе, через оптимизированную в Zemax линзу, была проведена трассировка лучей с использованием разработанной моделирующей программы. Для моделирования геометрооптического распространения лучей через линзу использовались соотношения, приведённые в работах [50 – 52]. На рис. 3а показаны точечные диаграммы для трёх длин волн, полученные с использованием моделирующей программы.

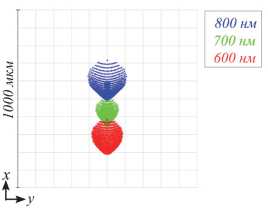
Рис. 2. Точечные диаграммы, полученные в Zemax для трёх длин волн 600 нм, 700 нм, 800 нм (снизу вверх соответственно). Шаг сетки на рисунке составляет 100 мкм

Из рис. 3 б видно, что, полученные в Zemax и моделирующей программе, точечные диаграммы имеют почти идентичную форму и размеры, что свидетельствует о корректности работы программы геометрооптического моделирования. В дальнейшем данная программа будет использоваться в качестве фрагмента программы, моделирующей распространение световых волн через линзу в приближении скалярной волновой теории. Далее рассмотрим математический аппарат, использованный для моделирования прохождения световой волны через линзу и расчёта (кодированной апертуры) фазовой или эйкональной функции на её входной плоскости.

а)        .—. 50 мкм ^—^У                0)        ■—■ 50 мкм

Рис. 3. Точечные диаграммы пятен рассеяния линзы для трёх длин волн 600 нм, 700 нм, 800 нм (слева направо): полученные в моделирующей программе (а); в сравнении с диаграммами в Zemax (выделены цветом) (б)

координатами (u, v). В настоящем исследовании было выбрано, что входная и выходная плоскости перпендикулярны оптической оси и проходят непосредственно через вершины соответствующих поверхностей линзы. За выходной плоскостью на расстоянии г2 расположена плоскость изображения с декартовыми координатами (х,у). Рассматриваемый источник из точки (х0 = —М, у0 = —S') испускает сферическую волну, которая проходит, через входную плоскость и попадает на первую асферическую поверхность линзы. После прохождения второй сферической поверхности линзы, на которую нанесена дифракционная решётка, образуется сходящаяся сферическая волна. Эта волна проходит через выходную плоскость и фокусируется в окрестности точки c координатами (х = М + Ах, у = S) плоскости изображения, где Ах — смещение точки фокусировки в зависимости от длины волны и порядка дифракции.

Связь комплексной амплитуды в выходной плоскости и плоскости изображения в общем случае имеет вид:

Е (х,^) =

= f _ _oA₂(u,^ехр(1к^₂(и,v))G(x,у,и,v)dudv, (1)

где G (х, у, и, v) — ядро интегрального преобразования, А₂(и, v),^₂(и, v) — амплитуда и эйконал в плоскости (и, v) .

Пусть у нас есть лучевое преобразование, связывающее плоскости (^, п) и (и, v) . Это преобразование представим в виде: и = U(^, п), v = V(^, п) . Данное преобразование легко найти, используя законы геометрической оптики.

Перейдём от интегрирования по координатам (и, v) , к координатам (^, п) :

Е(х, у) = JOA^Utf, riVtf, rf) х х ехр [ik^2{U(^,riVtf,ri)) х хG(x, y,U(^, riVtf, p))dudv.(2)

Обозначим:

Ф2(^, п) = Ч^Ъn),V(^ п)),(3)

В свою очередь эйконал в выходной плоскости можно представить как:

где Ф₁(^, п) - эйконал в точке (^, п) на входной плоскости, L(^,п) - длина оптического пути от точки входа (^, п) до точки выхода с координатами (и, v) .

Перепишем выражение (2) в виде:

где якобиан J&p) = \^д^ > ^д^ — ^д^ > ^д^\.

^д               '^{п 17}        д^ д^ д^ д^

Интенсивности в плоскостях (^, п) и (и, v) связаны законом сохранения светового потока:

I1&п)^п, и, v) cosafon⁾d^dn =

= 1₂(и, v) cos в(и, v)dudv,                      (7)

где а(^, п) - угол между лучом и нормалью в плоскости (^, п) , Р(и, v)— угол между лучом и нормалью в плоскости (и, v) , т(^, п, и, v) — пропускание среды.

Отсюда, амплитуды связаны соотношением:

Обозначим y⁽^, п) =в(и^, п), v⁽\, п)) , Х&п) = = т(^,п, и(^, п), v(^, п)) . В итоге выражение (6) с учётом (5) и (8) можно представить в виде:

Е(х, у) =                      _____

= f -0 E i (?, п)Т&п) G(x,у,$,п)41Ыd^dп, (9) где E i ⁽^, п) = A i (^, п⁾ехр(1кФ 1 ⁽^, п)) — это комплексная амплитуда в точке с координатами (^, п) , а функция:

m п) =     _______________

= exp(ikL⁽^, п))7х⁽^, п) cos а⁽^, п^)/cos у⁽^, п) (10) описывает изменение амплитуды и эйконала волны между точками (^, п) и (и, v) .

Полученное соотношение (9) позволяет вычислить поле в плоскости изображения по координатной сетке входной плоскости. Данный подход может быть использован для моделирования распространения поля через N оптических систем.

• 2.2.    Градиентный метод расчёта ДОЭ

Связь между входным Е¹(и, v) и выходным Е¹⁺¹(х, у) сигналами при распространении в свободном пространстве в общем виде имеет вид:

Е¹⁺¹(х,у) = f Е¹(и, v)G(x,у, и, v)dudv,       (11)

где G(x, у, и, v) — ядро интегрального преобразования.

Представим интеграл (11) в дискретном виде, при этом для простоты, описание осей координат в дальнейшем опустим:

Е^Ах,у) = Х рд Е^и р , v_q)G(x_i , у ) , и_р, v^AuAv =

= ЬмЕ^Р™,(12)

где ядро преобразования Р?Е = G(x_^ , у ) , и_р, v^&u&v .

Рассмотрим нашу оптическую систему. Поле на входной плоскости (^, п) ДОЭ:

Е1 = ТмЕ^,(13)

где Е_р[ , — поле в предметной плоскости (х₀, у₀).

Поле, после прохождения ДОЭ:

Uy = Ацехр^^Е1, где Ai) — учитывает изменение амплитуды, а Фу — длины оптического пути от точек входа с координатами (^, п) до точек выхода с координатами (и, v).

Выражение для поля в плоскости изображения ⁽х, у) :

Е^ = ЪМ™,                (15)

где Q ^ — ядро преобразования.

Рассмотрим расчёт фазовой функции на входной плоскости ДОЭ путём минимизации некоторого функционала. В качестве такого функционала выберем квадратичный функционал, выражение для которого имеет вид [53]:

£ = ~' Lt j (ji j - b i] ) ^ min,                    (1⁶⁾

где Ц ] — интенсивность в плоскости изображения, b ij — заданное распределение интенсивности.

Найдём приращение функционала, вызванное приращением фазовой функции Vp,_q :

дЕ = Zij(!ij - bij) dlij,(17)

dij = (дЪМ”)(ЬМ+

+(ЪМ%%д^^(18)

где * - означает комплексное сопряжение.Далее получаем:

dlij = Re{(^pq ди^)(^(и^П(19)

где с учётом (14):

TtVq^dUv_qQ^ =

= Xpq d^q{iApqeXp(i^q)E^q^.(20)

Подставляя (19), (20) в (17) получаем:

дЕ = Z pq dV ^q Re{X ij (/ ij — b ij ) x

X ((I^^QOX^^expQM-pJ/^(21)

Тогда выражение для градиента функционала (16) имеет вид:

V pq ^E = ^Re{L ij ⁽^ ij - ^b ij) ^x

X (^st(UhQiN(i{Apqexp(^^^^^(22)

Рассмотренный функционал ошибки (16) накладывает условие как на значения, так и на форму распределения интенсивности в плоскости изображения. Для решения задачи расчёта ДОЭ может быть достаточным условие фокусировки в заданную область. В таком случае выражение для квадратичного функционала имеет вид:

Е = f (S a hj - b) ^ min,                 (23)

где b — значение интенсивности в области фокусировки П .

Проводя аналогичные действия с функционалом, получим выражение для градиента:

V pq E = $_а1ц -b) x

X Re{X a (X_s t (UhQij)y

(^A pq eXp^ pql E pqWq ).                 (24)

Полученные соотношения легко модифицируются для случая нахождения градиента функционала, вызванного приращением эйкональной функции на входной плоскости. Отметим, что рассмотренный выше подход может быть использован для нахождения приращения функционала для оптической системы, состоящей из нескольких ДОЭ.

• 2.3.    Метод Adam для расчёта ДОЭ

В настоящей работе для минимизации функционала применялся метод стохастической оптимизации Adam (Adaptive Moment Estimation). Данный метод широко используется во многих отраслях науки и техники, где задачи можно свести к оптимизации некоторой скалярной параметризованной целевой функции с учётом условия её максимизации или минимизации относительно её параметров. Метод вычисляет индивидуальные адаптивные скорости обучения для различных параметров на основе оценок первого и второго моментов градиентов [54]. Расчёт приближений целевой (фазовой или эйкональной) функции T осуществлялся по следующему алгоритму:

• 1)    Вычисляется распространение поля от предметной до входной плоскости ДОЭ и от выходной плоскости ДОЭ до плоскости изображения. Далее вычисляется комплексносопряжённое поле (X s _t(U s _tQi j ^t)) в плоскости изображения.

• 2)    По формулам аналогичным (22) или (24) вычисляется градиент функционала V_pqE , вызванный приращением целевой функции.

• 3)    Осуществляется расчёт нового приближения целевой функции на шаге n по формуле:

• 3.    Вычислительный эксперимент по расчёту ДОЭ

  • 3.1.    Исходные параметры расчёта

• 3.2.    Расчёт фазовой функции

T_n = T_n _! — а • т П /(4ъ П + е), (25) где параметры а — величина шага, е — малая константа (для предотвращения деления на нуль) задаются, а in, v — оценки первого и второго моментов с поправкой на смещение вычисляются по соотношениям, приведённым в работе [54].

Для расчёта использовалась математическая модель асферической линзы, представленная в данной работе. Входная плоскость линзы имела форму зрачка с диаметром 10 мм и разбивалась с шагом 10 мкм. Размер плоскости изображения в сагиттальном направлении составлял около 2 мм, тогда как в направлении дисперсии размер изображения определялся диаметрами геометрооптических пятен рассеяния и спектральным диапазоном, в котором проводился расчёт. Дискретизация в плоскости изображения также составляла 10 мкм. Расчёты проводились с учётом фокусировки световых пучков в спектре первого порядка. Следует отметить, что параметры линзы, полученные в первом разделе, были оптимизированы для диапазона длин волн от 600 до

800 нм, что позволяет выбрать в данном диапазоне информативные длины волн для вычисления определённых вегетационных индексов. Ниже приведены результаты вычислительных экспериментов по фокусировке излучения для выбранных длин волн из рассматриваемого спектрального диапазона.

На первом этапе был проведён эксперимент по расчёту фазовой функции на длине волны Л = 700 нм с учётом фокусировки по полосе захвата оптической системы линзы. Для этого в плоскости изображения задавалось 5 точек фокусировки, которые в сагиттальном направлении имели координаты: – 1 мм, – 0,5 мм, 0 мм, 0,5 мм, 1 мм (которые соответствовали 5-ти сферическим точечным источникам в предметной плоскости). Таким образом, на каждой итерации приближение фазовой функции вычислялось для 5-ти падающих пучков. Необходимо отметить, что координаты точек фокусировки выбирались такими же, как при оптимизации линзы в Zemax, с добавлением дополнительных точек с координатами – 0,5 мм и 0,5 мм. Это было сделано с целью формирования фазовой функции, которая учитывает фокусировку в промежуточных точках поля зрения линзы.

Вид вычисленных фазовых функции представлен на рис. 4.

Из рис. 4 видно, что, полученные результаты расчёта для двух вариантов начальных фаз, имеют схожую картину фазовых профилей. На рис. 5 показаны распределения интенсивности в плоскости изображения, полученные на длине волны 700 нм от сферического точечного источника в предметной плоскости. При этом в расчёте фазовая функция на входной плоскости линзы не учитывалась.

Из рис. 5 видно, что распределение интенсивности находится внутри области с размерами приблизительно 120×120 мкм. На рис. 6 показаны распределения интенсивностей в плоскости изображения для центра и краёв поля зрения, полученные с аналогичными параметрами расчёта. При этом в расчётах учитывались фазовые функции на входной плоскости линзы. Распределения интенсивностей внутри поля зрения, как для координат у = -0,5 мм и 0,5 мм (на рис 6 не показаны), так и всех остальных сагиттальных координат имеют схожий характер.

Полученные распределения интенсивностей локализованы в области с размерами приблизительно 30×30 мкм для всех точек поля зрения линзы. Полученные результаты позволяют перейти ко второму этапу исследования, на котором необходимо провести оценку возможности фокусировки излучения в два узких спектральных канала, что в свою очередь позволит использовать линзу для получения индексных изображений.

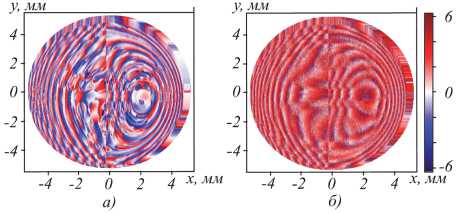
Рис. 4. Фазовые функции на входной плоскости линзы, рассчитанные при начальной фазе:(а) нулевой, (б) случайной

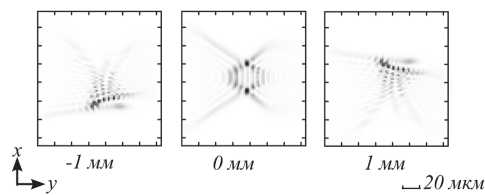
Рис. 5. Распределения интенсивностей в плоскости изображения в окрестности точек фокусировки в центре и на краях поля зрения без учёта рассчитанной фазовой функции

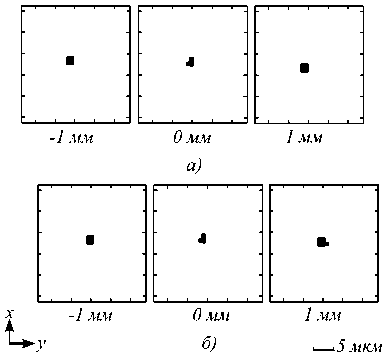
Рис. 6. Распределения интенсивностей в плоскости изображения в окрестности точек фокусировки по сагиттальной координате (– 1 мм, 0 мм, 1 мм) для двух вариантов фазовой функций на рис. 4 (а) и (б)

• 3.3.    Расчёт эйкональной функции

На втором этапе был проведён вычислительный эксперимент по расчёту эйкональной функции для длин волн Л. = 650 нм и Л₂ = 750 нм . Длины волн были выбраны для получения изображения нормализованного дифференцированного вегетационного индекса NDVI [55]. Аналогично 3.2 в плоскости изображения для каждой длины волны задавалось 5 точек фокусировки, которые в сагиттальном направлении имели координаты: – 1 мм, – 0.5 мм, 0 мм, 0.5 мм, 1 мм. Таким образом, на каждой итерации приближение эйкональной функции вычислялось для 10-ти падающих пучков. Вид вычисленной эйкональной функции представлен на рис. 7.

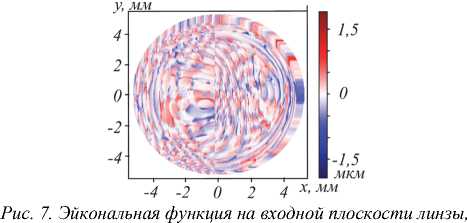
рассчитанная при нулевом начальном эйконале

На рис. 8 представлены распределения интенсивности в плоскости изображения для центра и краёв поля зрения, полученные для длин волн 650 нм и 750 нм с учётом рассчитанной эйкональной функцией. Распределения интенсивностей внутри поля зрения, как для координат у = -0,5 мм и 0,5 мм (на рис. 8 не показаны), так и всех остальных сагиттальных координат имеют схожий характер.

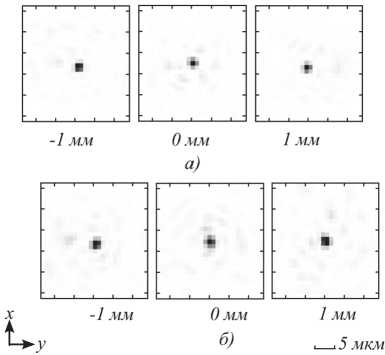
Рис. 8. Распределения интенсивностей в плоскости изображения в окрестности точек фокусировки по сагиттальной координате (– 1 мм, 0 мм, 1 мм) для двух длин волн 650 нм (а) и 750 нм (б)

Вычисленные распределения интенсивностей также локализованы в области приблизительно 30×30 мкм для всех точек поля зрения линзы.

4.    Расчёт передаточных характеристик ДОЭ

Для оценки способности оптической системы формировать изображение был проведён расчёт функций рассеяния точки (ФРТ) спектральной линзы, с учётом того, что параметры пучка, падающего на предметную плоскость со стороны объектива, будут соответствовать      дифракционно-ограниченному объективу с диафрагменным числом к = 3. Полученные результаты расчётов ФРТ не значительно отличаются от вида распределений на рис. 8. Для оценки способности оптической системы передавать пространственные частоты в изображении предмета и оценки качества изображения обычно используется частотно-контрастная характеристика (ЧКХ) [56, 57]. На рис. 9 показаны ЧКХ линзы для двух спектральных каналов.

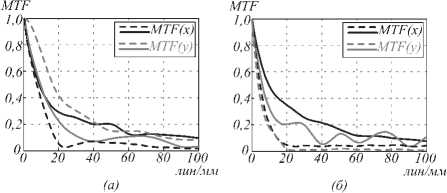
Рис. 9. ЧКХ соответствующие ФРТ на длинах волн 650 нм (а) и 750 нм (б). Сплошной линией показаны ЧКХ, полученные с учётом эйкональной функции на входной плоскости, пунктирной – без учёта

Значения ЧКХ на частоте 20 лин / мм в направлении дисперсии составляют 0,29 и 0,35 для длин волн 650 нм и 750 нм соответственно. В сагиттальном направлении – 0,22 и 0,20 соответственно. Для теоретической оценки передачи пространственных частот оптико-электронной системой обычно используется функция передачи модуляции (ФПМ), определяемая произведением ФПМ звеньев такой системы [58]. Показанная на рис. 1 оптическая схема спектральной линзы хорошо сочетается с формфактором объектива современного смартфона (длина оптической части ~ 5 – 6 мм), для которой характерное значение ЧКХ (или ФПМ) на частоте 20 лин / мм составляет более 0,9 [59]. В качестве регистратора можно выбрать фотоприёмник, например NOIL2SM1300A [60], для которого геометрическая ФПМ на рассматриваемой пространственной частоте составляет 0,88. Тогда суммарная теоретическая ФПМ на частоте 20 лин / мм в меридиональном направлении составляет 0,23 и 0,28 для длин волн 650 нм и 750 нм соответственно, а в сагиттальном 0,17 и 0,16 соответственно. Формируемое изображение в направлении полосы захвата с использованием выбранной фотоприёмной матрицы будет иметь приблизительно 140 пикселей. Проведённая оценка показывает, что компактная оптико-электронная система, основанная на данной спектральной линзе, способна передавать пространственные частоты на изображении объекта.

5.    Обсуждение

В рамках настоящего исследования была изучена и продемонстрирована потенциальная возможность использования обычной двояковыпуклой линзы в качестве дисперсионного элемента, который формирует распределение освещённости в спектре первого порядка для выбранных длин волн. Общая длина оптической системы от апертурной (щелевой) диафрагмы до монохромной матрицы составила 63 мм. Стоит отметить, что длина полосы захвата линзы (2 мм) совпала с полосой компактного спектрометра [23]. Формфактор данной линзы был получен с использованием инструментов трассировки и локальной оптимизации Zemax. Спектральное разделение было достигнуто за счёт использования фазово-кодированной апертуры, расположенной в плоскости перед первой асферической поверхностью линзы и дифракционной решётки на второй поверхности линзы. Кодированная апертура вычислена с использованием моделирующей программы, написанной на языке программирования Python, и, основанной на математических соотношениях, полученных в настоящей работе. При этом, моделирование распространяющихся из предметной плоскости расходящихся сферических пучков проводилось на основе вычисления интегралов Кирхгофа. Расчёт спектрального разделения был проведён для двух длин волн 650 нм и 750 нм для получения изображения нормализованного дифференцированного вегетационного индекса NDVI [55], однако потенциально может быть выбрана другая комбинация каналов для задач [12 – 20] в диапазоне длин волн от 600 до 800 нм. Показано, что компактная оптико-электронная система, построенная на базе такой линзы, позволяет передавать пространственные частоты в изображении контрастных объектов. Полученная спектральная линза не отличается компактностью от известных современных схем дисперсионных датчиков [22 – 30] или датчиков на светофильтрах [31 – 41]. Однако видится, что её преимуществом является большая доступность, т.е. простота конструкции и низкая стоимость изготовления, как и [47, 48], что является ключевым фактором для использования такой линзы в интересах задач сельского хозяйства и точного земледелия. Конструктивным отличием данной системы от [46 – 49] является реализация спектрального разделения и фокусировки без использования дополнительной коллимирующей оптической системы. Следует отметить, что использование, разнесённых на разные поверхности кодированной апертуры и сферической дифракционной решётки позволяет для последней использовать технологию изготовления нарезной решётки [61], что потенциально может значительно повысить светосилу в узких каналах. Перспективой будущих исследований является рассмотрение некоторых из возможных ограничений в применении данной линзы, связанных с чувствительностью к технологическим погрешностям изготовления, температурными изменениями, рассеянием т.п. Также представляются интересными исследования возможности реализации фазово-кодированной апертуры на входной криволинейной поверхности линзы, увеличения поля зрения и числа узких спектральных каналов и т.п.

6.    Заключение

В настоящей работе исследована возможность использования обычной собирающей линзы в качестве дисперсионного элемента, формирующего изображение на монохромной фотоприёмной матрице в узких спектральных каналах. Формфактор данной линзы был получен с использованием Zemax, спектральное разделение в узкие каналы получено за счёт использования фазово-кодированной апертуры, расположенной в плоскости перед первой поверхностью и дифракционной решётки на второй поверхности линзы. Вычислена эйкональная функция для разделения излучения на длинах волн 650 нм и 750 нм. Расчётным методом показано, что компактная оптико-электронная система, построенная на основе такой спектральной линзы, способна передавать пространственные частоты на контрастном изображении предмета.    Главным отличием спектральной линзы от известных миниатюрных спектральных систем является использование обычной собирающей линзы в качестве элемента осуществляющего спектральное разложение и формирование изображения на монохромной матрице.

Низкая стоимость изготовления, лёгкость, компактность и простота конструкции позволяют использовать спектральную линзу в качестве полезной нагрузки на борту большого числа БАС, например с целью решения мониторинговых задач в области точного земледелия и сельского хозяйства.

Перспективой будущих работ является исследование возможности реализации фазово-кодированной апертуры на входной криволинейной поверхности линзы, увеличения поля зрения и числа узких спектральных каналов линзы и т.д.

Статья подготовлена при финансовой поддержке Министерства науки и высшего образования Российской Федерации, грант № 075-15-2025-610.