Расчёт стигматической линзы с минимальными френелевскими потерями

Линзы являются базовым компонентом многих оптических систем. Несмотря на долгую историю (линзы были изобретены еще до нашей эры), расчёт асферических линз с заданными оптическими свойствами по-прежнему остаётся актуальной научной и практически значимой задачей [1 – 11]. В частности, в работах [1, 2] рассмотрен аналитический расчёт стигматических линз, у которых первая поверхность является заданной, а вторая рассчитывается из условия постоянства оптической длины пути лучей для двух сопряженных точек. Такая линза для выбранной пары точек не имеет сферической аберрации, т.е. преобразует сферический волновой фронт, исходящий из точки-объекта в сходящийся сферический волновой фронт с центром в точке параксиального изображения. В работах [3 –8] рассмотрен расчёт апланатиче-ских линз с двумя асферическими поверхностями. У апланатических линз, помимо условия стигматичности (условия постоянства оптической длины пути лучей для двух сопряженных точек), дополнительно выполняется условие Аббе [12], обеспечивающее отсутствие комы. Отметим, что расчёт апланатической линзы является более сложной задачей. Если объект расположен в бесконечности, то расчёт линзы сводится к решению системы уравнений, содержащих два нелинейных алгебраических уравнения и одно обыкновенное дифференциальное уравнение первого порядка, разрешённое относительно производной [3, 4]. В общем случае, когда объект и изображение расположены на конечных расстояниях, расчёт аплана-тической линзы требует решения сложного нелиней- ного дифференциального уравнения, не разрешённого относительно производной [8].

При прохождении света через линзу на преломляющих поверхностях линзы происходит частичное отражение света, обусловленное разными значениями показателей преломления по обе стороны поверхностей линзы. Данные потери описываются формулами Френеля [13]. При большом числе линз в оптической системе, а также при большой угловой апертуре линз френелевские потери могут быть очень существенными. Кроме того, наличие неконтролируемого отраженного света снижает контраст формируемого изображения. Для «борьбы» с френелевскими потерями используется просветление оптики. Однако простые оптические покрытия позволяют эффективно уменьшить отражение только при определенных углах падения и длинах волн. В настоящей работе рассмотрен еще один механизм снижения френелевских потерь, основанный на определенном методе расчёта поверхностей линзы. Как отмечено выше, при расчёте стигматической линзы одна из поверхностей линзы может быть задана произвольным образом [1, 2]. Это показывает, что в общем случае линза с двумя асферическими поверхностями позволяет не только убрать сферическую аберрацию, но и дополнительно обеспечить выполнение ещё одного заданного условия. В настоящей работе впервые рассмотрен метод расчёта линз с двумя асферическими поверхностями, имеющих минимальные френелевские потери в классе стигматических линз. Минимизация френелевских потерь достигается за счёт одинаковых углов девиации лучей на поверхностях линзы [14, 15]. При этом расчёт стигматических линз с минимальными френе- левскими потерями сведен к решению обыкновенного дифференциального уравнения, разрешённого относительно производной. Для указанных линз также получены простые аналитические аппроксимации.

Расчёт стигматической линзы из условия минимума френелевских потерь

Рассмотрим расчёт осесимметричной линзы (показатель преломления n > 1), отображающей источник излучения, расположенный в начале координат в среде с показателем преломления n 0 = 1, в точку ( f , 0) на оптической оси, также расположенную в среде с единичным показателем преломления (рис. 1). Для простоты будем рассматривать только линзы, строящие действительное изображение источника. Пусть первая поверхность линзы задана функцией длины радиус-вектора R ( ф ), где угол ф отсчитывается от оптической оси. Обозначим у ( ф ) угол между преломленным на первой поверхности лучом и осью z . Определим вторую поверхность линзы через функцию l = l ( ф ), описывающую длину пути лучей в линзе (рис. 1), в следующем параметрическом виде:

z 2 ( ф ) = R ( ф ) cos ф + l ( ф ) cos у ( ф ) , У 2 ( ф ) = R ( ф ) sin ф + 1 ( ф ) sin у ( ф ) .

Запишем условие постоянства оптической длины пути лучей от точечного источника до его изображения:

^ = R ( ф ) + nl ( ф ) + ^У 22 ( ф ) + ( f - z 2 ( ф ) ) ² = const. (2)

Рассматривая центральный луч, распространяющийся по оси z , значение оптической длины пути V представим в виде

V = R 0 + nl 0 + ( f - [ R 0 + l 0 ] ) = ( n - 1) l 0 + f ,        (3)

где R 0 = R (0) – расстояние от источника до первой поверхности, l = l ( ф ) - толщина линзы.

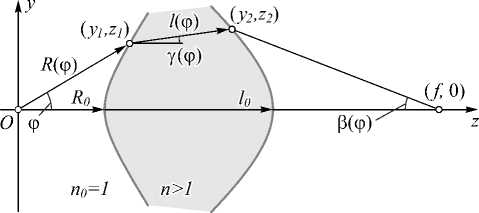
Рис. 1. Геометрия задачи расчёта линзы

Из уравнений (1), (2) следует, что при расчёте стигматической линзы без дополнительных ограничений имеется определенная свобода в выборе одной из поверхностей линзы. В данном случае, при определении второй поверхности в виде (1), первая поверхность R (ф) может быть выбрана произвольно. Действительно, при некоторой заданной функции R (ф) функция у (ф) выражается через функцию R (ф) и её производную с использованием закона Снеллиуса, и тогда расчёт стигматической линзы сводится к отысканию функции l = l (ф) из уравнений (1), (2). Несложно видеть, что расчёт функции l = l (ф) сводится к решению квадратного уравнения.

Далее мы используем указанную «свободу» для расчёта стигматической линзы с дополнительным условием, соответствующим условию минимума френелевских потерь. Для этого подставим (1) в (2) и выразим R ( ф ) через l ( ф ) в виде

R ⁽ф ) =

• V ² - f ² + 1 ( ф ) [- 2 n V + 2 f cos у ( ф ) + ( n ² - 1 ) l ( ф ) ] (4) 2 [v- f cos ф+ ( cos ( ф-у ( ф ) ) - n ) l ( ф ) ]

Известно, что минимизация френелевских потерь достигается при одинаковых углах девиации лучей на поверхностях оптического элемента [14, 15]. Углы девиации лучей на первой и второй поверхностях линзы равны 5 1 = ф - у ( ф )и 5 2 = у ( ф )- в ( ф ) соответственно. Здесь углы ф , у и в (рис. 1) определены с учетом следующего правила знаков. Углы отсчитываются от оптической оси и считаются положительными при направлении отсчёта против часовой стрелки. Углы, отсчитываемые в направлении по часовой стрелке, являются отрицательными. В этом случае углы ф , у являются положительными, а угол в ( ф ) - отрицательным. Полагая 5 1 = 5 2 , получим

Р ( ф ) = 2 у ( ф ) -ф-                                 (5)

С другой стороны, из геометрии задачи (рис. 1) и условия постоянства оптической длины пути лучей (2) будем иметь:

sin ( -в ( ф ) ) = sin ( ф- 2 у ( ф ) ) =

=_________ У 2 ( ф ) _________ =       У 2 ( ф )            (6)

" V У 22 ( ф ) + ( f - z 2 ( » ))' "  ^V R И- ^nl ^

Подставляя (1) в (6), несложно получить l (ф) в виде l (ф) =

V cos ( ф-у ( ф ) ) - f cos у ( ф )

- 1 + n cos ( ф-у ( ф ) )

Далее, подставляя (7) в (4), выразим R ( ф ) через у ( ф ) в виде

R ⁽ф ) =

• -V+ f csc ( ф-y ( ф ) ) ^ n sin ( ф- 2 у ( ф ) ) + sin у ( ф ) ] (8)

  - 2 + 2 n cos ( ф-у ( ф ) )

Закон преломления лучей на первой поверхности линзы можно представить в виде следующего дифференциального уравнения [15– 17]:

dln R (ф)       sin (ф-Y(ф))dф       1/ n - cos (ф-Y(ф))

Прологарифмируем (8), затем вычислим производную

dy(Q) dф

= F (ф, Y(ф)) =

dln R ( ф )/d ф и приравняем полученный результат к правой части выражения (9). Тогда после простых, но утомительных вычислений получим для у ( ф ) обыкновенное дифференциальное уравнение, разрешённое относительно производной:

n - cos (ф-Y(ф))]■[-1 + n cos (ф-Y(ф))] sin у (ф)

4 f (1 + n2) sin ф- n |^4T sin3 (ф-у(ф)) + f {sin (2ф- 3у(ф)) + 3sin (2ф-у(ф)) + 6sin у

. (10)

Таким образом, расчёт стигматической линзы с минимальными френелевскими потерями (с одинаковыми углами девиации лучей) сводится к выполнению следующих шагов:

• 1.    Решение дифференциального уравнения (10).

• 2.    Расчёт 1 ( ф ) по формуле (7).

• 3.   Расчёт R ( ф ) по формуле (4).

При решении дифференциального уравнения (10) используется граничное условие у (0) = 0. Данное условие предполагает, что центральный луч, распространяющий вдоль оптической оси, не преломляется. Заметим, что правая часть дифференциального уравнения (10) (функция F ( ф , у ( ф ))) имеет неопределенность «0/0» при ф = 0. Чтобы избавиться от этой неопределенности, учтём, что у ( ф ) по правилу знаков является нечетной функцией. Полагая в правой части (10) у ( ф ) = аф + аф ³ + О ( ф 5 ), получим:

F (0, у(0)) = Um F (ф, у(ф)) = а.                (11)

Значение а = F (0, у (0)) можно выразить через значение R 0 , соответствующее расстоянию от источника до первой поверхности, толщину линзы l 0 и координату f точки изображения. Действительно, подставляя Y ( ф ) = аф + аф ³ + О ( ф ⁵) в (8) и вычисляя предел R = lim R ( ф ) , получим:

ф^0 v 7

Действительно, вышеприведённое выражение для R ( ф ) легко получить из закона преломления (9) при у ( ф ) = аф , а выражение для 1 ( ф ) получается из уравнения (7), которое записано с учетом условия постоянства оптической длины пути (2). Отметим, что уравнения (14) описывают стигматическую линзу, для которой уравнение (8), записанное с учетом условия равенства углов девиации лучей на поверхностях линзы, в общем случае выполняется приближённо. Представленный в следующем параграфе пример расчёта линзы показывает, что формулы (14) хорошо аппроксимируют параметры линзы, рассчитанные на основе точных формул (10), (7) и (4). Более того, в некоторых частных случаях приближённые аналитические формулы (14) соответствуют точным решениям. Рассмотрим эти случаи.

Случай 1. Если линза расположена посередине между источником и изображением (при этом f =2 R 0 + l 0 ), то из соображений симметрии следует, что одинаковые углы девиации достигаются при Y ( ф ) = 0, то есть при а = 0 в (14). В этом случае формулы (14) принимают вид:

R (ф) = R о

n - 1

n cos ф- 1

R 0

f (n + а- 2 n а) + (а-1)V 2 (n - 1)(а-1)

1 (_Ф) Л cos ^ф f n cos ф- 1

.

С учетом (3), из последнего уравнения значение а может быть получено в виде:

1 f (n-1) а = 1 +--------------- f - 2 fn + 2( n-1) R0 + V

= 1__ f—

2 f - 2 R - 1 о

. (13)

Таким образом, чтобы рассчитать линзу при заданных значениях R 0 , l 0 , f , необходимо вычислить а = F (0, y (0)) по формуле (13).

В окрестности ф = 0 можно положить у ( ф ) «аф . При у ( ф ) = аф функции R ( ф ) и 1 ( ф ) несложно получить в аналитическом виде:

R (ф) = R о

n - 1

n cos ( ф-аф ) - 1

1 -а

,

V cos (ф-аф)-f cos (аф) -1 + n cos (ф-аф)

.

Формулы (15), как и следовало ожидать, представляют линзу, у которой поверхности являются гиперболами. Первая гипербола преобразует расходящийся сферический пучок от источника в коллимированный, а вторая гипербола преобразует коллимированный пучок в сходящийся пучок со сферическим волновым фронтом с центром в точке (0, f ). Поскольку при Y ( ф ) = 0 в ( ф ) = - ф (см. (5)), то полученная линза также удовлетворяет условию Аббе [12].

Случай 2. Если изображение находится в бесконечности, то в ( ф ) = 2 Y ( ф )- ф = 0 и Y ( ф ) = ф /2. В этом случае поверхности линзы описываются выражениями (14) при а =1/2.

В заключение данного параграфа приведем ряд формул, позволяющих «связать» точную линзу, определяемую уравнениями (10), (7) и (4), с соответствующей параксиальной линзой. Как отмечено выше, в окрестности угла ф = 0 точная линза может быть описана аналитическими выражениями (14).

Используя (14), можно вычислить радиусы кривизны линзы при ф = 0:

f - 2 fn + 2 (n -1) R о + V г R                      , f (n-1) + 2 (n -1) R о + V

_— ( fn - ( n - 1) R 0 -^Х" f + 2( n - 1) R о + V ) r ²         ( n - 1) ( f + fn - 2( n - 1) R 0 -V )

если интенсивность Штреля опускается не ниже 0,8 [19]. Отсюда следует, что условие стигматичности у данной линзы выполнено с высокой точностью.

у, град

.

6 -

5 -

Eq. (10) ---Linear

Приведенные радиусы кривизны описывают параксиальную линзу, соответствующую как точной линзе, так и линзе (14). При необходимости, используя формулы толстой линзы [13], ограниченной двумя сферическими поверхностями, можно рассчитать положения главных плоскостей и фокусные расстояния линзы. Кроме того, в рамках аппроксимации у ( ф ) = аф , в ( ф ) = 2 аф - ф = ф (2 а -1), и можно получить линейное и угловое увеличения линзы:

sin ф 12 jmag —          —--+ О(ф ) ® 1

sin в ( ф )   2 а- 1             2 R + l ₀

_ tg в ( ф ) _ sin в ( ф )_ 1

1mag —           ~ .       — tg ф sin ф    Lmag

Пример расчёта

Для иллюстрации полученных в предыдущем параграфе теоретических результатов рассмотрим пример расчёта линзы со следующими параметрами: расстояние от источника до первой поверхности R 0 =20 мм, толщина линзы L 0 =20 мм, координата точки изображения f = 80 мм, показатель преломления материала линзы n = 1,5. На рис. 2 а показана функция у ( ф ), рассчитанная из решения дифференциального уравнения ДУ (10), и её линейная аппроксимация Унп ( ф ) = аф при фе [0,35 ° ]. При указанных выше параметрах а = 0,2. Из рис. 2 а видно, что при выбранных параметрах точно рассчитанная функция у ( ф ) близка к линейной функции.

На рис. 2 б показана сама линза, импортированная в программу оптического проектирования Zemax [18]. Следует отметить, что линза, рассчитанная по приближенным аналитическим формулам (14), оказывается визуально неотличимой от линзы на рис. 2 б , рассчитанной на основе точных формул (10), (7) и (4). При этом нормированные среднеквадратичные отклонения профилей линзы, рассчитанных по точным формулам, от профилей (14) составляют менее 0,11 %.

На рис. 2 в показано рассчитанное в программе Zemax сечение в плоскости изображения дифракционной функции рассеяния точки, сформированной линзой с числовой апертурой NA = sin35 ° = 0,57 на длине волны X = 0,5876 мкм. Относительная интенсивность в главном максимуме диска Эйри (интенсивность Штреля [13]) составила I st = 0,99. Напомним, что изображение точечного источника считается еще не отличающимся от дифракционно-ограниченного,

4 -

2 ■

/ - ф, град

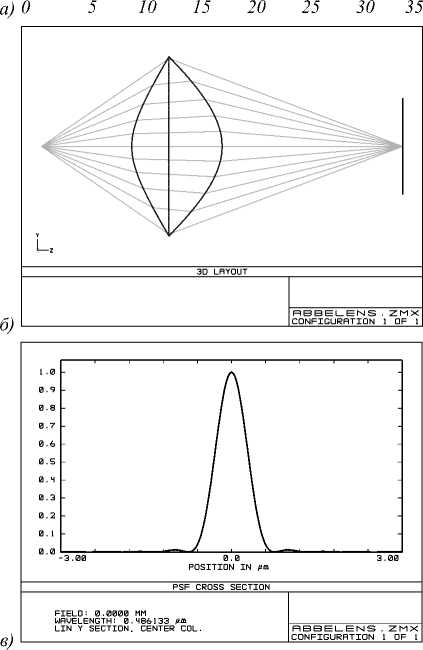
Рис. 2. Функция у(<р), рассчитанная из решения дифференциального уравнения (10) (непрерывная серая линия), и её линейная аппроксимация (чёрная пунктирная линия) (а); изображение линзы в рабочем окне программы Zemax (б); рассчитанное в программе Zemax сечение в плоскости изображения дифракционной функции рассеяния точки (в)

Для фе [0,35 ° ] в программе Zemax были рассчитаны углы девиации лучей на поверхностях линзы. Условие равенства углов девиации лучей также оказалось выполненным с высокой точностью, что подтвердило правильность представленных теоретических результатов и выполненных расчётов.

Рассчитанная в программе Zemax методом трассировки лучей эффективность линзы, определяемая как доля излученного источником светового потока, попадающая в пятно Эйри, при изотропном источнике излучения составила 87%. Таким образом, френелевские потери для рассчитанной линзы равны 13 %. Следует отметить, что при выбранных параметрах углы падения лучей на поверхности линзы варьируются от нуля до 64,9° для первой поверхности и от нуля до 32,4° для второй поверхности. При этом френелевские потери для неполяризованного света изменяются от 8 % для центрального луча (ф = 0) до 18,7 % для крайнего луча (ф = 35°). Важно отметить, что практически такие же френелевские потери получаются и для линзы, рассчитываемой на основе аналитических формул (14).

Интересно отметить, что стигматическая линза, рассчитанная из условия минимума френелевских потерь, приближенно удовлетворяет условию синусов Аббэ [12]:

sin ф sin в ( ф )

= const = L mag .

При выбранных параметрах линейное увеличение параксиальной линзы, определяемой формулой (17), равно L mag = –1,667. На рис. 3 приведен график функции

S _m ag ^(ф)

L mag

sin ф sin (2у(ф)-ф)   mag

представляющей относительное изменение увеличения рассчитанной линзы при фе [0,35 ° ]. Из рис. 3 следует, что относительное изменение увеличения при фе [0,35 ° ] не превышает 3,5%. Практически такое же изменение увеличения имеет место и для линзы, рассчитанной на основе аналитических формул (14).

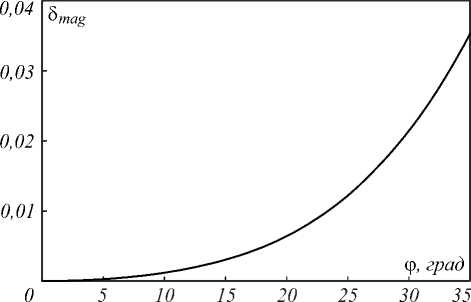
Рис. 3. График функции 3 mag (<р), описывающей относительное изменение увеличения линзы

Практический интерес представляют и аберрационные свойства стигматической линзы с минимальными френелевскими потерями. Расчёт, выполненный с помощью программы Zemax при числовой апертуре NA = sin20 ° = 0,34, показал, что качество изображения внеосевой точки близко к дифракционно-ограниченному (интенсивность Штреля не ниже

0,8) при ее удалении от оптической оси на 0,15 мм, а оптимизация по коэффициентам обоих асферических поверхностей позволяет увеличить это отклонение до 0,33 мм. При этом коэффициент комы 3-го порядка почти на порядок больше у оптимизированной линзы, что говорит о роли этой аберрации в коррекции вращательно не симметричных аберраций высших порядков, играющих значительную роль даже при столь ограниченной апертуре.

Заключение

Рассмотрен расчёт линз с двумя асферическими поверхностями, имеющих минимальные френелевские потери в классе стигматических линз. Минимизация френелевских потерь достигается за счёт одинаковых углов девиации лучей на поверхностях линзы. Расчёт линзы сводится к решению обыкновенного дифференциального уравнения, разрешённого относительно производной. Получены простые аналитические аппроксимации для профилей линзы. Представленный пример расчёта линзы подтверждает правильность полученных расчётных формул и демонстрирует хорошую точность аналитических аппроксимаций для профилей линзы.

Работа выполнена при поддержке гранта РФФИ (проект № 18-29-03067) в части разработки метода расчёта линзы, Российского научного фонда (проект № 20-19-00081) в части численного исследования оптических свойств линзы и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части создания программных средств для расчёта линзы.