Расчёт устойчивости двухслойных уступов грунтовых выемок при упругопластическом распределении напряжений

Решение проблемы обеспечения долговременной устойчивости уступов откосов и бортов карьеров имеет особую актуальность в горном деле и в строительстве, так как от их параметров зависит безопасность разработки месторождений полезных ископаемых [1] и строительства различных зданий и сооружений в приоткосных зонах.

В работах [2–4] приводятся результаты исследований и расчётов устойчивости однородных и двухслойных уступов откосов грунтовых выемок с использованием задач теории упругости. Однако в реальных условиях при коэффициентах устойчивости, близких к единице (т. е. в наиболее интересных для практики случаях), в приоткосной зоне имеются как упругие, так и пластические области.

Точное решение упругопластической задачи представляет значительные математические трудности, не оправданные точностью полученных результатов. Используемые в расчётах значения физико-механических характеристик грунтов определяются довольно приблизительно. Параметры грун- тов практически всегда являются величинами неточными из-за случайных ошибок, которые связаны с естественной природой самого объекта и ошибками (погрешностями), возникающими при отборе образцов грунта для проведения опытов. Кроме того, неточности могут быть обусловлены неопределенностями, связанными с технологией определения параметров (погрешности аналитических устройств и неточная их калибровка) [4]. Поэтому целесообразно упругопластическую задачу решать приближенно. К тому же в практике проектирования укоренилось некритичное отношение к выбору расчетных моделей и реализующих их программ [5, 6]. Возможность использования приближенного аналитического решения смешанной задачи теории упругости и теории пластичности грунта для предварительной оценки несущей способности пластов грунта была также подтверждена в работе [7].

В работе [8] исследуется устойчивость однородных уступов откосов при упруго-пластическом распределении напряжений в приоткосной зоне. При этом сделаны два допущения: 1) наиболее вероятная поверхность скольжения, построенная по методике [9], с появлением пластической области не изменяет своё положение значительно; 2) вертикальные составляющие напряжений с пере- ходом массива откоса в предельное состояние также практически не изменяются и определяются упругим решением. Эти допущения обоснованы результатами экспериментальных исследований на моделях из эквивалентных материалов. Получены формулы для определения напряжений в пластической и упругой областях, разработана методика определения границы между этими областями.

В частности, получены выражения для вычисления горизонтальных и касательных безразмерных напряжений (в долях у H , где Y — объёмный вес грунта, H - высота откоса) в пластической области:

нию, выполненному для однородных откосов. Разница состоит в том, что при построении наиболее вероятных поверхностей скольжения напряжения определяются решением задач теории упругости для слоистых откосов, и, так как слои имеют разные физико-механические характеристики, параметр устойчивости является функцией координат точек приоткосной зоны. Очевидно, что в таком случае (аналогично как и для однородных откосов) величина коэффициента устойчивости, вычисленная из решения упругой и упругопластической задачи, практически одинакова.

Если поверхность разрушения полностью проходит по контакту слоёв, то в каждой её точке известно положение площадки разрушения. Поэтому при решении задачи в этом случае остаётся одно

σ

y

σ _x (1 - m ) - λ m

;

1 + m

τ

xy

0, 5 m (2 σ _x +λ )tg2 α 1 + m

где ст x - вертикальная составляющая безразмер

ных напряжений; m = sin в cos2( a - (45 ° + 0,5 ф ));

a - угол наклона уступа; в — угол заложения откоса; X - параметр устойчивости, зависящий от фи-

зико-механических характеристик грунта;

Х =         ,

γ H tg ϕ

где C - удельное сцепление; ф - угол внутреннего

трения.

Методика проведения исследований

При решении упругопластических задач для слоистых откосов возможны три случая: 1) наиболее вероятная поверхность разрушения пересекает слои; 2) полностью совпадает с контактной зоной слоёв; 3) частично совпадает с контактными зонами слоёв.

В первом случае решение упругопластической задачи реализуется подобно реше-

допущение, состоящее в том, что с появлением в приоткосной зоне пластической области вертикальная составляющая напряжений почти не изменяется и определяется решением соответствующих задач теории упругости для слоистых откосов.

При частичном совпадении поверхности разрушения с контактом слоёв решение упругопластической задачи представляет, очевидно, комбинацию решений, рассмотренных в первых двух случаях.

Решение последней задачи дало результаты, качественно совпадающие с аналогичными результатами, полученными для однородных откосов.

Установлено, что значительное влияние на устойчивость откосов оказывает величина коэффициента бокового давления грунта (как для одноступенчатых [10–12], так и многоступенчатых [9]).

На рис. 1 представлена расчётная схема грунтовой выемки с углом откоса β = 35° и уступами, каждый из которых имеет угол заложения a = 60°.

Принято полагать [13, 14], что накладываемые на расчетную конечно-элементную схему граничные условия практически не влияют на распределение напряжений при удалённости границ расчетной области от ее исследуемой части не менее чем на 6 максимальных размеров этой области.

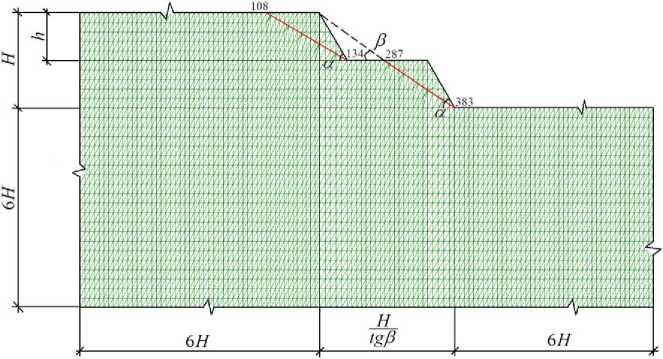
Рис. 1. Схема к расчёту устойчивости уступов двухступенчатого борта при β = 35°; α = 60°

Основания и фундаменты, подземные сооружения

Таким образом, горизонтальный размер модели принят равным 12 + —— | H , а вертикальный - 7 H

I tg PJ

( Н – высота откоса). Грунтовый массив, вмещающий откос с уступами, сложен слоями пород, «падающими» в сторону выемки. Принято, что наиболее вероятная поверхность разрушения полностью совпадает с контактом слоёв, а угол наклона контактной поверхности в каждом рассматриваемом случае равен углу наклона откоса.

На представленной схеме контакт слоёв проходит через точки 108–134 и 287–383, то есть поперечное сечение верхнего слоя – треугольник, нижнего – вся остальная область.

Пусть E 1 и ξ 01 – соответственно модуль упругости и коэффициент бокового давления грунта верхнего слоя, а E 2 и ξ 02 – нижнего. Примем следующие значения указанных характеристик: E ₁: E ₂ = 0,1; ξ 01 = 0,75; ξ 02 = 0,3 [15, 16].

Для анализа напряжённо-деформированного состояния приоткосной зоны с учётом областей пластических деформаций в рассматриваемом грунтовом массиве и определения коэффициента устойчивости двухслойного уступа применён метод конечных элементов (МКЭ), формализованный в компьютерной программе [17]. Вопрос сходимости решён посредством сравнения результатов, полученных посредством МКЭ для расчётной схемы однородного грунтового массива, с соответствующими результатами, полученными по методике, основанной на точном решении задач теории упругости для весомой изотропной полуплоскости с трапециевидными вырезами по её границе [2, 18], аналогично тому, как это сделано в работах [3, 8]. Кроме того, проверка адекватности выбора размеров расчетной модели проводилась при помощи сопоставления численных значений напряжений в различных ее точках, вычисленных при помощи метода конечных элементов [19], с численными значениями соответствующих напряжений, вычисленных на основе использования методов теории функций комплексного переменного [18, 20].

Анализ результатов

На рис. 2 приведены эпюры распределения безразмерных напряжений вдоль контакта слоёв, полученные из решения задач теории упругости (сплошные линии). Величина коэффициента устойчивости для принятых характеристик грунтов:

— = 5,53 Х + 1,1. (3) tg в

Значение угла внутреннего трения принимаем φ = 13°. Полагая в формуле (3) K = 1, можно определить значение параметра устойчивости λ = 0,587, при котором откос находится в предельном состоянии.

На рис. 3 указаны эпюры удерживающих и сдвигающих сил, построенные по напряжениям, определённым из упругого решения при φ = 13° и λ = 0,587 (кривые CD и BE), действующих вдоль контакта слоёв. Наименьшее значение коэффициента устойчивости соответствует точке 360. Приравнивая в этой точке удерживающие и сдвигающие силы при φ = 13°, получим λ = 1,31. Определённые два значения параметра λ позволяют вычислить по формуле (2) высоту борта карьера H _пр, при которой нижний уступ ( h _пр. = 0,5 H _пр.) находится в предельном состоянии ( h _пр = 8,76 Сγ ^–1; К = 1) и h _уп = 3,93 Сγ ^–1, при которой в приоткосной зоне нет областей пластических деформаций (при λ = 1,31; К = 1,9). Таким образом, при высоте нижнего уступа h <  h _n p ( K >  1,9) в приоткосной зоне не может возникнуть областей пластических деформаций, а значит, справедливо упругое решение [2]. При ^h уп <  ^h <  Й пр ⁽¹ >  K >  1,9) в приоткосной зоне имеется область пластических деформаций и следует при определении устойчивости использовать решение упругопластической задачи [8].

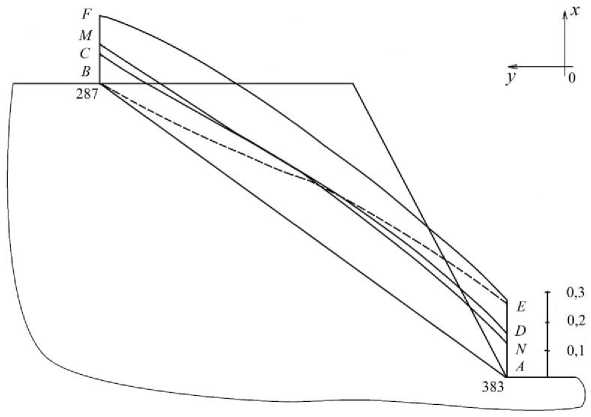
Рис. 2. Эпюры удерживающих и сдвигающих сил

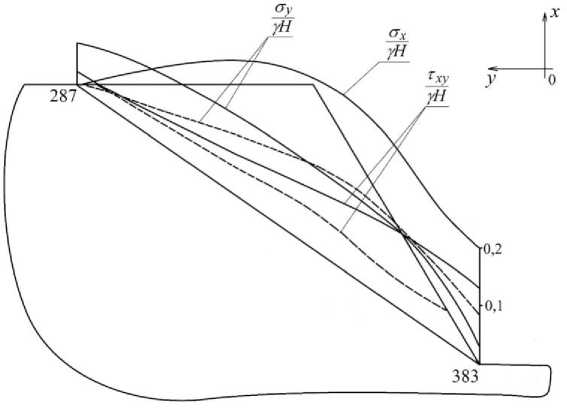
Рис. 3. Эпюры безразмерных напряжений

Рассмотрим предельное состояние уступа (φ = 13°, λ = 0,587). Напряжения в точках поверхности разрушения определяются посредством формул (1).

Сравнение величин напряжений показывает, что с появлением пластической области и переходом откоса в предельное состояние горизонтальные и касательные составляющие напряжений значительно перераспределяются. Касательные составляющие напряжений убывают практически вдоль всего контакта, горизонтальные составляющие в приоткосной области выше, чем полученные из упругого решения, но по мере удаления от этой зоны в массиве они становятся близки к ним. С приближением к дневной поверхности горизонтальные составляющие резко уменьшаются.

При использовании значений полученных напряжений построены эпюры безразмерных удерживающих и сдвигающих сил, указанные на рис. 3, из которого заметно, что удерживающие силы, определённые решением смешанной задачи (кривая MN ), практически совпадают с удерживающими силами, определёнными упругим решением (кривая CD ). Картина распределения сдвигающих сил при различных решениях выглядит по-разному, однако сумма этих сил, действующих вдоль всей поверхности разрушения, одинакова (отличие величин составляет 4 %). Значит, упругое и упругопластическое решение при переходе грунтового массива в предельное состояние дают одинаковые значения сумм удерживающих и сдвигающих сил, а следовательно, и величин коэффициентов устойчивости откоса.

Исследования, проведённые для слоистых откосов с другими физико-механическими характеристиками грунта, дали аналогичные результаты.

Выводы

Таким образом, в заключение можно отметить, что с появлением в приоткосных зонах уступов областей пластических деформаций происходит перераспределение горизонтальных и каса- тельных составляющих напряжений, а также действующих вдоль поверхности разрушения сдвигающих сил. Вертикальные составляющие напряжений и удерживающие силы, практически не изменяясь, определяются упругим решением [2, 3]. При этом сдвигающие силы перераспределяются так, что в сумме остаются примерно такими же, как и полученные при помощи упругого решения, поэтому величины К, определяемые как отношение суммы удерживающих к сумме сдвигающих сил, при использовании решений упругопластической и упругой задач практически одинаковы.