Расчёт величин деформации при формовании обувных материалов параболоидом вращения

При формовании заготовок верха обуви раздвижной колодкой, которая имеет сложную пространственную поверхность, деформируемый материал испытывает одновременное растягивающее воздействие в различных направлениях. Исследования способности материала для верха обуви деформироваться, принимать и сохранять приданную ему форму проводятся с помощью различных приборов и устройств, в которых моделируется двухосное растяжение образцов. В большинстве случаев такие устройства реализуют процесс деформирования плоских материалов с помощью жёстких пуансонов, имеющих форму различных тел вращения: сфера, цилиндр или тор. Общим для них является формование образцов, жёстко закреплённых по их периметру, в виде круга, причём радиус рабочей части испытываемого образца или совпадает или меньше общего радиуса формующего пуансона. Технические нормовые правовые акты, а также авторы многих методик, посвященных проблемам формования и формоустойчивости, рекомендуют исследования деформационных свойств обувных материалов производить двухосным растяжением с помощью шарика небольшого диаметра или пуансоном в виде жёсткой сферы (рис. 1 а, б), то есть когда деформирование осуществляется сферической поверхностью [1 – 4]. Однако только некоторые элементы обувной колодки и только в первом приближении можно считать сферическими. Также следует учесть, что сфера, как тело вращения, имеет лишь один линейный параметр – радиус, величина которого определяется в зависимости от радиуса рабочей части испытуемого образца. Процесс формования обувных материалов несферической поверхностью описан А. Ю. Зыбиным в работе [5]. В приборе В 3030 конструкции А. Ю. Зыбина для обеспечения однородного деформационного состояния в пробе используется пуансон в виде стакана с радиальными пазами и вмонтированными в них подвижными роликами, которые образуют замкнутое кольцо, имитирующее поверхность тора (рис. 1  в).

Деформирование образцов материалов поверхностью вращения в виде тора, на наш взгляд, имеет преимущество перед продавливанием сферой, заключающееся в том, что такая поверхность характеризуется двумя линейными параметрами: радиусом окружности, образующей тор вращения, и расстоянием от её центра до оси вращения. Величины указанных параметров, а также их соотношение между собой и радиусом рабочей части образца позволяют при проектировании новых приборов и устройств, в основу которых положен принцип продавливания, более близко моделировать процесс формования заготовок верха обуви.

Рисунок 1 – Схемы нагружения образцов материала при двухосном растяжении

Указанными выше преимуществами перед сферой обладает не только тороидальная поверхность, но и другие поверхности тел вращения, например эллипсоид вращения. Расчёт получаемых величин деформаций при продавливании образцов на определённую высоту поверхностью эллипсоида вращения сопряжён с определёнными математическими сложностями [6]. Поэтому целью данной работы является получение расчетных формул для определения величин деформации, которые испытывает плоский образец в виде круга при его деформировании более простой несферической поверхностью. Такой поверхностью выбрана поверхность в виде параболоида вращения.

Так как материалы для заготовок верха обуви имеют толщину значительно меньшую, чем линейные размеры формующей обувной колодки, то при расчёте величин деформаций толщину образца учитывать не будем, то есть будем считать деформируемый образец абсолютно тонким. Указанное допущение может быть по необходимости устранено при использовании полученных результатов в проектировании продавливающих устройств, в которых рабочий радиус продавливаемой пробы материала невелик и толщина образца может существенно влиять на величины получаемых относительных деформаций.

Рассмотрим растяжение материала в виде плоского образца радиуса R параболоидом, который образован вращением параболы y= x2 вокруг её оси k симметрии. В формулу, задающую параболу вращения, введен дополнительный параметр, содержащий общий коэффициент кривизны k, который в дальнейшем может быть определён из соотношения между линейными размерами имитируемого элемента обувной колодки. Произведём расчёт значений относительного приращения площади образца и относительного удлинения по меридиану (относительной меридиальной деформации) в зависимости от высоты подъёма пуансона h (рис. 2).

Рисунок 2 – Схема растяжения материала в виде кругового образца поверхностью параболоида вращения

Величина относительного приращения площади определяется формулой:

s, = S S⁰ • 100% ,

s      _S0

где S₀ = n R - первоначальная площадь деформируемого кругового образца радиуса R = |ф | , а S - площадь поверхности образца после его продавливания в результате подъёма пуансона на высоту h = | cv | .

После продавливания площадь образца равна S = S 1 + S 2 , где S 1

–

площадь

боковой поверхности усечённого конуса с радиусами оснований R = | с | , r = | fe | и образующей l = | e | , а S ₂ - площадь материала непосредственно облегающего поверхность параболоида по дуге NE .

Осевое сечение параболоида вращения в системе координат Oxy представляет

I I R 3

собой параболу, уравнение которой с учётом того, что | OV | = — = const , имеет вид:

RR ³ у =-- x² +---.

kk

На рисунке 2 часть этой параболы с вершиной в точке N , расположенной в первой четверти системы координат Oxy , изображена дугой NEA .

Для вычисления площадей S₁ и S₂ определим координаты точки касания

E ( xo; ^yo ) •

Для нахождения ординаты этой точки найдём уравнение касательной LB к

R3

параболе, заданной уравнением (2) при подъёме пуансона на высоту 0 <  h <— [7].

k

2R

Т ак как значение производной в точке касания у (х₀) =-- х₀ , то уравнение

0 k 0

касательной в точке касания E ( х₀;у₀ ) имеет вид:

2Rx          Rx ² R ³

у =--- •( х - хй)--- + —, k    0kk

или

2Rx     Rx ² R ³

у =--- • х + —- + —.

k kk

Координаты точки B , как точки пересечения касательной BL с осью абсцисс Ox ,

2Rx Rx ² R³

найдём из уравнения (4). При у = 0 имеем---хв +---1-- kBkk

или

R² + x 2

х„ =-------, а значит B

^B     2x 0 ^,

₇ ^{+ х}^ ;0 •

2х0     >

Учитывая подобие треугольников EKD и DAB, то есть

координаты точки B

KE kd

DA

Ab

и то, что    |ю | = R — x₀ ,

1 "I = k - h

aba=loBl - loAl=X-±X-- r = R2 - 2Rx*±x2 = (R x0)2,

соотношение

(5) и

принимает вид:

I KE1=

2 • x0 •

( X 3

I k

^

- h

)

^{R - x}o

Тогда ордината точки касания E ( x₀;y₀ ) равна

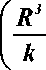
h I. ^R ± ^X

) ^{R - x}o

Найдём абсциссу точки касания E ( x₀;y₀ ) , для чего в уравнение касательной

(   X3)

линии (4) подставим координаты точки D X;--h , которая принадлежит как

I   к)

параболе, так и касательной, а следовательно, удовлетворяет обоим уравнениям.

Таким образом, нахождение абсциссы координаты точки касания E (x0; у0) сводится к решению уравнения

X 2 2 • X2,

— • х_п--- x_n ± h = 0 . k⁰k⁰

„X² ± V X ' - kXh

.

Решение вышеприведенного уравнения имеет вид: х₀ =-------------

0 R

Так как абсцисса точки касания не может превышать радиуса R , то

Х0 =

X2 - Vx' - kXh

R

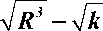
R3

k

- h

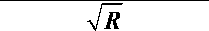
Введём следующие обозначения:

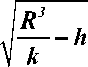
b = RR- - a • 4k .

Таким образом, точка касания E

b

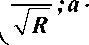
k

, а радиус круга

r = ^X0

= l""E|=4-.

R

Для определения площади боковой поверхности усечённого конуса, сечение которого в плоскости Oxy представляет собой трапецию, найдём длину образующей ED из треугольника EKD . Так как l = | ed | = ^| КЕ^ + |ю | , то значения длин векторов КЕ и KD :

I ®|=

7 I i3

² • x⁰ 'I k

h I ,        2    2 • a2 •2 • xo • a

R

R x0

R x o

i -

2 • a • b kk ’

R

| kd| = |cd| - d = i - x0 = i -

R

R

= a •

Подставляя полученные значения в формулу l = ^| ке| + | kd| , находим длину образующей l усечённого конуса.

l =

4 • a2 • b2 ------+

k

a2 • k   a • V4 • b2 • i + k2

R

RRr

•

Таким образом, площадь S 1 боковой поверхности усечённого конуса с радиусами оснований i = | cd | , r = | ее | и образующей l = | ed | равна:

С                 I» b ) a • V4b2i + k2

S, = n ( i + r ) • l = n l i + —;=--,-------

1 v 7 I  Rr J   URr

n a •

i • sk

•

Для определения площади S₂ , материала непосредственно облегающего поверхность параболоида по дуге NE , воспользуемся формулой нахождения площади поверхности тела вращения, полученного вращением дуги NE параболы

RR ³

у =-- x² + — вокруг оси ординат Oy [5]:

kk

S 2 = 2 n y E x(y) • V 1 + ( x'(y) ) ² dy •

yN

Из уравнения параболы (2) получим зависимость переменной x от переменной y, Vi3 - k • y которая выражается формулой x = -—. Для определения значения площади поверхности вращения найдём производную функции x(y) по переменной y:

x ‘ (y)

= i3 - k • y I

R

k

2 • Ri • Vi3 - k • y

Подставляя значения функции x(y) и её производной x ‘ (y) в формулу (11), получаем площадь поверхности вращения:

n

R

Rr+ + b a--/=—

k

J

R3 k

S 2

R3++b a k

= 2П J

R3

7R3 - k • y

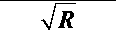
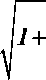
k ²

4 • R • ( R³ - k• y )

dy =

74R4 + k2 - 4 • k • R • y dy = I -

R 3 + + b a •---;=—

k

3 • 4 • k • R R

k

п

6 • k • R²

•

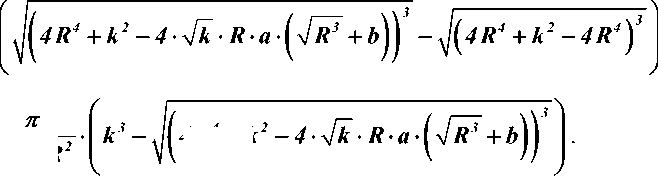
4R + k

6 • k • R

Введём обозначение

c = ^( 4 • R4 + k2 -

.

Тогда площадь поверхности тела вращения, полученного вращением

R 2 R ³

параболы y =-- x +--, имеет следующий вид:

kk

дуги

NE

nAk³ -c³ )

S2 =—---

²     6 • k • R²

.

Используя полученные формулы (10) и (13), получаем, что площадь

кругового

образца после его продавливания пуансоном в форме параболоида вращения на высоту h , будет вычисляться по формуле:

п-a •

S = S1 + S2 =----

2 n(k3 -c3) ” + 6 • k • R2

или

n

S = —

'2 • R + k2 + k3 - c3)

6 • k • R2

.

Тогда, используя формулы (1) и (14), находим относительное полное приращение площади образца после продавливания его на высоту h пуансоном в форме параболоида вращения:

6 • a • R • 4k •(b + 7R3)• 74 • b2 • R + k2 + k3 - c3 - 6 • k • R4

E s

6 • k • R⁴

• 100%

Полученная расчётная формула (15) содержит только три переменные: высота

R продавливания h, радиус образца R и коэффициент кривизны k параболы y =--x2, k при вращении которой вокруг оси симметрии образован параболоид вращения.

Параметры a , b и c зависят только от указанных исходных параметров h , R , k и определяются соответственно по формулам (8), (9) и (12).

Далее найдём величину относительной меридиальной деформации.

Величина относительной меридиальной деформации:

= m = L7L⁰- • 100% ,

L0

где L₀ = 2R - первоначальный диаметр деформируемого кругового образца радиуса R = -CD, , а L - длина образца после продавливания на высоту h по меридиану.

Найдём L . Длина образца по меридиану равна сумме длин образующей усечённого конуса и дуги параболы, непосредственно лежащей на поверхности параболоида вращения, то есть:

L = 2 • ( I ne + ED ) .

_                                     I ^-^ i , a • V 4 • b² • R + k²            _

Длина образующей усечённого конуса: ED = l =-----,   ----. Таким образом,

V k • R для определения длины образца по меридиану необходимо найти только длину дуги

R ,             С R3)             I b параболы y =--x2 от точки N 0;— до точки E —j=;a • k              (   k J           IVR

R

k

b

R

k

.

Так как длина дуги кривой y = f (x) на промежутке [ а ; в ] находится по формуле

, в L         Л2 ,                           г l1 = J V1 + ( f (x)) dx , то длина дуги NE параболы y =--x2 равна:

1 г v 'k

b

x(E )                           R2

I ne = J 1 + + ( f (x) ) dx = ) J 1 + —₂— x² dx •

x( N )                         0

Применяя замену x ---tgt , вычисление дуги кривой сводится к вычислению

2 • R определённого интеграла:

2b R                                2b R arctg                                               arctg k kdt k kdt =---- 1+ + tg2t---== =

2 • R 0              cos t 2 • R 0 cos t

k

2^И

2b R arctg

Jk

2b R

(cost + sin²t) dt = Jk2 Y cos³1          2 • R ^J

2bR arctg dt k ^k

--+ ^7

cos t 2 • R '

sin2 t dt cos3t

Для вычисления второго полученного определенного интеграла применим интегрирование по частям.

Тогда длина кривой NE вычисляется с помощью двух определённых интегралов:

или

2bR arctg =— I *

2 • R   ^J 0

dt cos t

k sin t

+---- 2—

4 • R cos t

2b R arctg

2b R arctg k ^kdt

4 • R 0 cos t

iNE

k

4 • R

2b R arctg

dt cos t

tgt cos t

iwi arctg

k

4 • R

in

tg

( t П

) + tgt • ^ 1 + tg²t

J

2b R arctg

После преобразования

1 I t n in tg — +—

1 2 4

= ln tgt + 7 1 + tg²t

формула для вычисления

длины дуги параболы упрощается и имеет следующий вид:

или

l NE

k

4 • R

( In tgt + ^ 1 + tg²t + tgt •

7 i + tg²t )

2b R arctg

i = k ^NE 4 • R

ln

2b R       22b R tgarctg —-— + J1 + tg arctg —-—

2b^ Г 2    2b4R

+ tgarctg —- J 1 + tg arctg —-—

k

4 • R

(

• in

2b R      4b2R

-----+ _A 1 +-- T-k          k²

2b^ I  4b2 R

--_A 1 +--- T-k \ k

С учётом координат точек

(   R3 ^

N 0;— I и V ^k J

E

b

—j= ;a • R

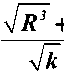
окончательно

формула имеет следующий вид:

i NE

1   (,₂ , 2b^ + 7 k² + 4b²R

--k • in-----------------------

4 • k • R                   k

V

)

+ bbRR • V k² + 4b²R

J

На основании формул (17) и (18) длина дуги, получаемой в сечении деформированного образца плоскостью Oxy , будет равна:

L = 2

4kR

k² • in

2 • b • 7 R + k2j ² + 4 • b² • R k

+ 2b V R • V k² + 4 • b² • R +

a • 7 k² + 4 • b² • R

aJ k • R

.

Введём обозначение

В результате получаем исходных параметров:

m = 7k2 + 4 • b2 • R .

формулу длины дуги L , которая зависит

только от

L = 2 •

( -L-

4 • k • R

V

(

• k² • in

V

2 • b • VR + m k

)

+ 2 • b • 7R • m + J

a • m

kkRR ^ .

Используя формулы (16) и (20) находим величину относительной меридиальной деформации при продавливании на высоту h параболоидом вращения:

L = 2 •

( z ( k2 • in

2 • b • VR + m

S m

4 • k • R

V

V

k

)

+ 2 • b • 7R • m +

J

a • m kjRR _?

- 2R

2R

• 100% ,

или после преобразования:

k² ⋅ ln

2 ⋅ b ⋅ R + m k

+ 2 ⋅ b ⋅ R ⋅ m + 2 ⋅ a ⋅ m ⋅ k ⋅ R - 4 ⋅ k ⋅ R²

ε _m

4 ⋅ k ⋅ R²

⋅ 100% .

Как и формула (15) формула (21) позволяет производить расчёт величины относительного удлинения деформированного образца по меридиану в зависимости только от значения высоты продавливания h и с учётом значений параметров a , b и m _, определяемых соответственно формулами (8), (9) и (19).

Полученные формулы (15) и (21) позволяют находить значения получаемых величин относительного приращения площади и относительной меридиальной деформации в зависимости от высоты подъёма пуансона параболоидной формы при продавливании образца в виде круга. Эти формулы могут быть использованы при конструировании различных приспособлений к разрывным машинам или самостоятельных приборов и устройств, в которых двухосное растяжение осуществляется жёстким пуансоном в форме параболоида вращения, который в отличие от наиболее часто применяемой стандартной сферической формы имеет большее колличество параметров. Построенная математическая модель процесса формования листовых материалов поверхностью параболоида вращения является одной из попыток приблизить лабораторные исследования деформационных свойств обувных материалов к реальному процессу формования заготовок верха обуви на обувной колодке.