Расчёт зеркала для формирования заданного непрерывного распределения освещённости на основе метода согласованных квадрик

Задача расчёта отражающей или преломляющей оптической поверхности из условия формирования заданного распределения освещённости в некоторой плоскости относится к классу обратных задач неизображающей оптики. Данная задача является крайне сложной и сводится к решению нелинейного дифференциального уравнения в частных производных второго порядка типа уравнения Монжа–Ампера. Методы расчёта оптических поверхностей, основанные на «прямом» численном решении уравнения данного типа, появились только в последние годы [1, 2]. В [1, 2] решение исходного нелинейного дифференциального уравнения сводится к решению системы нелинейных уравнений большой размерности (система содержит от нескольких тысяч до нескольких десятков тысяч нелинейных уравнений).

В общем случае для решения данной обратной задачи используются различные итерационные методы [3– 12]. Среди указанных итерационных методов особо следует выделить метод «согласованных квадрик» (supporting quadric method), предназначенный для расчёта зеркал или преломляющих оптических элементов, формирующих дискретные распределения освещённости в виде набора точек [9–12]. В зависимости от задачи в качестве квадрик используются параболоиды, эллипсоиды или гиперболоиды. В частности, в задаче расчёта зеркал поверхность зеркала представляется набором сегментов эллипсоидов или параболоидов (задача формирования дискретной диаграммы направленности). Расчёт параметров эллипсоидов (параболоидов) осуществляется итерационным методом, при этом сходимость метода строго доказана [10, 11]. Основными достоинствами метода согласованных квадрик (МСК) являются его универсальность и возможность формирования сложных дискретных изображений [12].

При решении светотехнических задач обычно требуется формирование непрерывных распределений в областях простой формы (прямоугольник, эллипс и т.п.). В работах [13, 14] МСК использовался для расчёта зеркал и преломляющих поверхностей, формирующих задан- ные непрерывные распределения освещённости. В частности, в [13] МСК применялся для определения вида функции лучевого соответствия (source-target map) в задаче расчёта зеркала для формирования постоянной освещённости в прямоугольной области. Функция лучевого соответствия определяет связь между угловыми координатами лучей, вышедших из источника, и декартовыми координатами точек прихода этих лучей (после отражения от зеркала) в выходную плоскость, где требуется формирование заданного распределения освещённости. Поскольку область излучения источника, как правило, задаётся некоторым телесным углом, то функция лучевого соответствия описывает некоторое отображение области на единичной сфере в заданную область в выходной плоскости. В [13] функция лучевого соответствия в задаче формирования непрерывного распределения освещённости определялась на основе непрерывной аппроксимации дискретного отображения, рассчитанного методом согласованных квадрик. По мнению авторов данной работы, недостатком метода [13] является необходимость восстановления поверхности зеркала по рассчитанной функции лучевого соответствия. В общем случае данная задача сводится к решению системы двух нелинейных дифференциальных уравнений в частных производных первого порядка.

В [14] МСК использовался для расчёта начального приближения при численном решении уравнения Монжа–Ампера. Как отмечено выше, решение данного уравнения сводится к решению системы нелинейных уравнений большой размерности. Решение такой системы остаётся задачей высокой вычислительной сложности.

В настоящей работе предложен новый метод расчёта отражающей поверхности, формирующей требуемое распределение освещённости в заданной двумерной области. В рамках метода поверхность зеркала представляется в виде двухпараметрического семейства эллипсоидов, у которых первые фокусы совпадают с источником излучения, а вторые фокусы принадлежат области, в которой необходимо сформировать заданное распределение освещённости. В работе показано, что такое представление поверхности является предельным случаем сегментированной поверхности, используемой в МСК для фокусировки в набор точек (точки фокусировки расположены в узлах прямоугольной сетки, аппроксимирующей заданную область). Огибающая поверхность имеет простой аналитический вид и зависит от функции, определяющей длины осей эллипсоидов семейства. При показателе преломления среды n = 1 данная непрерывная функция соответствует распределению эйконала в области фокусировки. Функция эйконала определяет распределение освещённости, формируемое в освещаемой области. Расчёт непрерывной функции осуществляется на основе непрерывной аппроксимации дискретной функции эйконала, полученной из решения дискретной задачи фокусировки в набор точек (точки фокусировки расположены в узлах прямоугольной сетки, аппроксимирующей заданную область). Работоспособность предложенного метода проиллюстрирована на примерах расчёта зеркал для формирования постоянной освещённости в областях различной формы.

1.    Представление поверхности зеркала

Рассмотрим задачу расчёта зеркала для формирования заданного распределения освещённости. Будем считать, что точечный источник излучения расположен в начале координат и излучает в пределах телесного угла Ω, соответствующего конусу с углом при

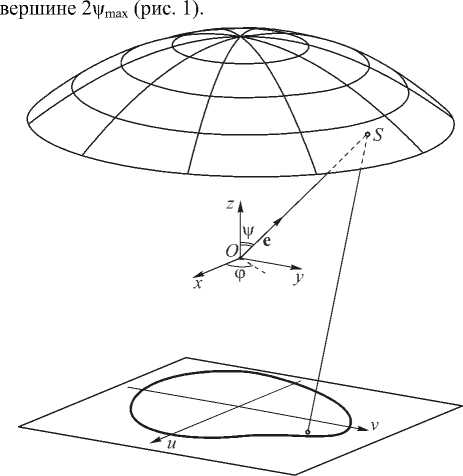
Рис. 1. Взаимное расположение зеркала, источника света и выходной плоскости

Интенсивность источника определяется функцией I(ф,у), где фе[0,2п], уе [0, у max] - углы сферической системы координат. Излучение от источника падает на зеркало, поверхность которого задаётся вектор-функцией S (ф, у). Задача состоит в расчёте функции S (ф, у) из условия формирования заданного распределения освещённости E (u), u е G , задан ного в плоскости z = f (f < 0), где u = ( u, v) - декартовы координаты в этой плоскости (рис. 1).

Рассмотрим сначала зеркало для фокусировки сферического пучка от источника в точку X ( u , v )=( u , v , f ) из области G . Такое зеркало является эллипсоидом с фокусами в начале координат (точка расположения источника) и в точке фокусировки X ( u , v ). В сферических координатах ( ф , у ) уравнение эллипсоида может быть представлено в виде [10]:

S ( ф , у ; u , v ) = е ( ф , у ) • l ( ф , у ; u , v ) ,                   (1)

где l (ф, у; u, v) =

___________ Р ( u , v ) ___________ 1 -e ( u , v ) ( е ( ф , у ), q ( u , v ) )

– расстояние от точечного источника до точки эллипсоида по направлению единичного вектора е ( ф , у ) = ( cos ( ф ) sin ( у ) ,sin ( ф ) sin ( у ) ,cos ( у ) ) ,

p ( u , v ) = ( V ² ( u , v ) - X ² ( u , v ) ) / 2 V ( u , v ) - фокальный параметр эллипсоида, V ( u , v ) - длина большой оси, e ( u , v ) = |X ( u , v )| / V ( u , v ) - эксцентриситет, q ( u , v ) = X ( u , v ) / |X ( u , v )| - единичный вектор направления на точку фокусировки. Отметим, что координаты точки фокусировки ( u , v ) в (1), (2) рассматриваются как параметры.

Существует бесконечное множество эллипсоидов, фокусирующих излучение от источника в точку X ( u , v ) . В качестве параметра, выделяющего конкретный эллипсоид, будем использовать длину большой оси V ( u , v ) . Отметим, что при показателе преломления среды n = 1 длина большой оси эллипсоида определяет эйконал в точке фокусировки. При заданном значении V ( u , v ) значения эксцентриситета и фокального параметра определяются по вышеприведённым формулам.

Далее рассмотрим расчёт зеркала, отражающего лучи из источника в область G , в которой должно быть сформировано требуемое распределение освещённости. Такое зеркало является огибающей семейства эллипсоидов (1), (2) по параметрам ( u , v ) е G . Действительно, по определению огибающая поверхность касается каждого из эллипсоидов семейства в некоторой точке. Поскольку направления нормалей огибающей поверхности и соответствующего эллипсоида в точке касания совпадают, то отражённый луч будет направлен в область G , в которой расположен второй фокус эллипсоида. Уравнение огибающей поверхности определяется системой уравнений, включающей уравнение эллипсоида (1) и следующие два уравнения [15 – 17]:

ds ds ds dи ’LЭф’ду _

= 0,

ds as as dv ’ Lдф’ду _

= 0.

Отметим, что условия равенства нулю смешанных произведений векторов в уравнениях (3) соответствуют условиям перпендикулярности нормального х    d s d s вектора эллипсоида N = —,—

L дф ду и касательных

к

-      -               ds координатным линиям огибающей поверхности — ди

и

—. Подставляя (1), (2) в (3), несложно преобразо-dv вать уравнения (3) к виду [15, 16]:

d l ( ф , у ; и , v )

ди д l (ф, у; и, v)

= 0,

av

= 0,

где функция l (ф, у;и, v) имеет вид (2). Интересно отметить, что уравнения (4) являются необходимым условием экстремума функции l (ф, у; и, v) по переменным (и, v) при фиксированных значениях переменных (ф, у). Данное условие позволяет представить огибающую поверхность в переменных (и, v) в виде:

s ( ф , у ) =

е ( ф , у ) •

____________ Р ( и ⁽ ф , у ) ) ____________

1 - е ( и ( ф , у ) ) ( е ( ф , у ), q ( и ( ф , у ) ) )

где

и(ф, у) = arg min l (ф, у; и, v), (и, v )= G или и(ф, у) = arg max l (ф, у; и, v). (и, v )gG

Уравнения (5)-(7) зависят от функции Т ( и , v ) , задающей длины больших осей эллипсоидов. Данная функция должна быть определена из условия формирования заданного распределения освещённости в области E ( u ) в области G .

• 2.    Связь с методом согласованных квадрик

Для объяснения метода расчёта функции Т(и, v) рассмотрим связь представления поверхности (5)-(7) с методом согласованных квадрик в задаче расчёта зеркала для фокусировки в набор точек X i =( ui, vi, f), i = 1,..., N. В методе согласованных квадрик поверхность зеркала состоит из сегментов эллипсоидов. При этом первые фокусы эллипсоидов совпадают с источником излучения, а вторые фокусы - с точками фокусировки Xi, i = 1,...,N . Расчёт больших осей эллипсоидов Тi, i = 1,...,N, проводится по итерационному алгоритму из условия формирования заданного распределения энергии в точках фокусировки [10, 11].

При заданных значениях Т i , i = 1,..., N поверхность зеркала, состоящего из сегментов эллипсоидов, определяется следующими соотношениями:

sd (ф, у) = е(ф, у) •;------, pm .----г,

^{1 -е} m ( ^{е (} ф , у )» q m )

где m = arg min l (ф, у; ui, vi)

i e{1,..., N } или m = argmax l (ф, у; ui, vi).(10)

i e { 1,..., N }

Значения фокальных параметров p i и эксцентриситетов е i = |X i | / Т i эллипсоидов (8) определяются через значения больших осей Т i , i = 1,..., N , по следующим формулам:

P i = ( т 2 - x 2 ) /2 Т i , е i = |X i .| / Т i .

Условие минимума (9) используется при расчёте зеркал эллиптического типа (в этом случае отражённые от зеркала лучи пересекают оптическую ось) [10, 11]. При условии (9) луч от источника с координатами ( ф , у ) направляется в точку фокусировки ближайшим к источнику эллипсоидом по направлению луча. Условие максима (10) используется при расчёте зеркал гиперболического типа (в этом случае отражённые от зеркала лучи не пересекают оптическую ось). В данном случае луч с координатами ( ф , у ) направляется в точку фокусировки самым далёким от источника эллипсоидом по направлению луча.

Несложно видеть, что уравнения (8)-(10) являются дискретным вариантом уравнений (5)-(7), в которых вместо области фокусировки X ( и , v ) = ( и , v , f ) , ( и , v ) е G и функции Т ( и , v ) , ( и , v ) е G используется набор точек X i = ( u_i , v i , f ) , i = 1,..., N и дискретный набор значений Т i , i = 1,..., N . Такая интерпретация позволяет рассматривать задачу фокусировки в двумерную область G как предельный случай дискретной задачи фокусировки в набор точек X i = ( u_i , v i , f ) , i = 1,..., N . При этом можно считать, что точки X _i , i = 1,..., N , расположены в узлах некоторой прямоугольной сетки, аппроксимирующей область G (рис. 2).

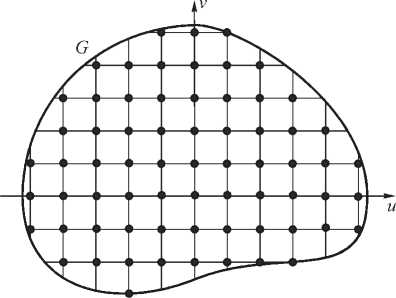
Рис. 2. Аппроксимация освещаемой области набором точек

3.    Метод расчёта

В пункте 1 в аналитическом виде получено общее представление поверхности зеркала, отражающего лучи из источника в заданную область G . Уравнения поверхности зеркала (5)–(7) зависят от функции Т ( u, v ) , ( u, v ) e G , которая должна быть определена из условия формирования заданного распределения освещённости в области E ( u ) в области G .

В пункте 2 показано, что задача фокусировки в двумерную область G является предельным случаем дискретной задачи фокусировки в набор точек X i = ( U i , v , f ) , i = 1,..., N .

Согласно вышеуказанным результатам пунктов 1, 2, в настоящей работе предлагается расчёт функции T ( u,v ) , ( u,v ) e G проводить через набор значений Т i , i = 1,..., N , определяющих параметры эллипсоидов в дискретной задаче фокусировки в набор точек X i , i = 1,..., N с заданным распределением энергии E i , i = 1,..., N . Будем считать, что точки X _i , i = 1,..., N , расположены в узлах некоторой прямоугольной сетки, аппроксимирующей область G (рис.2). При этом значения энергии в точках фокусировки определим через значения заданного непрерывного распределения освещённости в области G : E i = E ( u i , v i ) , i = 1,..., N . Для решения дискретной задачи разработан итерационный метод [10, 11]. При этом сходимость метода строго доказана. Если точки фокусировки расположены в дальней зоне, то расчёт Т i , i = 1,..., N может быть сведён к решению задачи линейного программирования [18, 19].

После решения дискретной задачи непрерывная функция Т(u, v), (u, v )e G может быть получена на основе построения непрерывной аппроксимации по значениям Тi, i = 1,...,N, заданным в узлах Xi, i = 1,...,N . В данной работе функция Т(u,v) определялась в виде сплайна. По рассчитанной функции Т (u, v) поверхность зеркала восстанавливается по аналитическим формулам (5)–(7). Высокие рабочие характеристики предложенного подхода проиллюст- рированы на ряде примеров, представленных в следующем пункте.

4.    Примеры расчёта зеркал

Предложенный метод был реализован в среде программирования Matlab. Продемонстрируем рабочие характеристики метода на примерах расчёта зеркал, формирующих выпуклые равномерные распределения освещённости в прямоугольной, эллиптической и треугольной областях.

Рассмотрим расчёт зеркала, формирующего равномерно освещённую прямоугольную область с размерами 6×4 м² в выходной плоскости, расположенной на расстоянии 10 м от точечного ламбертовского источника света. При этом будем считать, что точечный (компактный) ламбертовский источник излучает в полусферу, соответствующую области z >0 (рис. 1). Для решения данной задачи сначала методом согласованных квадрик было рассчитано зеркало для фокусировки в набор точек, расположенных в узлах эквидистантной сетки в заданной прямоугольной области. Была использована сетка с шагом 20 см. При выбранном шаге общее число точек фокусировки составило N =651 (31 точка по оси Ox и 21 точка по оси Oy ). В результате решения указанной дискретной задачи были получены значения функции эйконала в точках фокусировки (значения больших осей эллипсоидов Т i , i = 1,..., N ). Отметим, что решение дискретной задачи при указанном числе точек с помощью итерационного метода [10, 11] требует всего нескольких минут на стандартном персональном компьютере. Рассчитанные значения функции эйконала в точках фокусировки представлены на рис. 3. Для наглядности значения Ψ i , i = 1,…,651, показаны в виде точек на непрерывной поверхности.

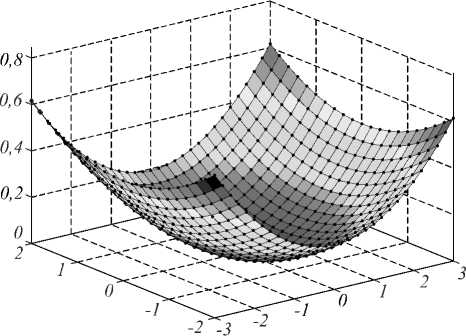
Рис. 3. Функция эйконала для фокусировки в набор точек в прямоугольной области

Для проверки правильности расчётов было проведено моделирование работы рассчитанного зеркала в программе для светотехнических расчётов TracePro® с использованием метода трассировки лучей [20]. Для этого по формулам (8)–(9) была рассчитана сегментированная отражающая поверхность. Затем полученная поверхность была аппроксимирована системой неоднородных рациональных сплайнов (NURBS) в программе автоматизированного проектирования

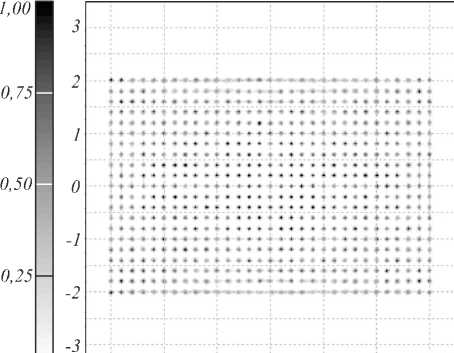
Rhinosceros® [21]. Указанная аппроксимация необходима для импортирования рассчитанной поверхности в программу TracePro®. Отметим, что аппроксимация сегментированной поверхности (8)–(9) гладкой функцией в виде набора рациональных сплайнов неизбежно приводит к некоторой ошибке. На рис. 4 показано рассчитанное в программе TracePro® распределение освещённости, формируемое зеркалом при точечном ламбертовском источнике излучения. Распределение освещённости рассчитано при 500000 лучей и показывает фокусировку в заданный набор точек. Некоторая неравномерность распределения энергии в точках фокусировки объясняется погрешностью метода трассировки лучей, а также погрешностью аппроксимации сегментированной поверхности (8)–(9) с помощью рациональных сплайнов.

E v. м

и, м

-3-2-10123

Рис. 4. Полутоновое распределение освещённости, формируемое сегментированным зеркалом для фокусировки в набор точек в прямоугольной области

Затем по рассчитанным значениям эйконала Ψ i , i = 1,…,651 с помощью аппроксимации бикубическим сплайном на равномерной сетке, состоящей из 6 патчей по оси Ox и 4 патчей по оси Oy , была построена непрерывная функция эйконала Ψ( u , v ). На рис. 5 показана поверхность зеркала, восстановленная по полученной непрерывной функции эйконала согласно

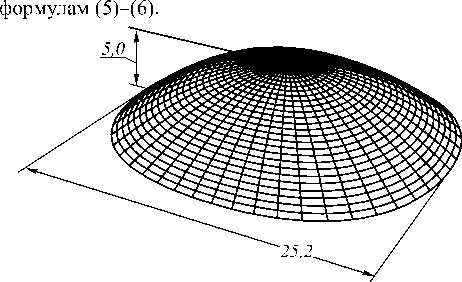
Рис. 5. Отражающая поверхность, формирующая равномерное распределение освещённости в прямоугольной области (габаритные размеры зеркала указаны в мм)

На рис. 6 представлено распределение освещённости, формируемое полученной отражающей поверхностью с точечным ламбертовским источником излучения. Данное распределение рассчитано в программе Trace Pro при 500000 лучах. Относительное среднеквадратическое отклонение (ОСКО) формируемого распределения освещённости от требуемого постоянного распределения освещённости составляет 6,8 %.

Е v, м

а)      -3  -2  -10   12  3

Е

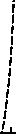
б)    -4

-2

Рис. 6. Распределение освещённости, формируемое зеркалом на рис. 5, при точечном источнике излучения: полутоновое распределение освещённости (а); профили распределения освещённости (б)

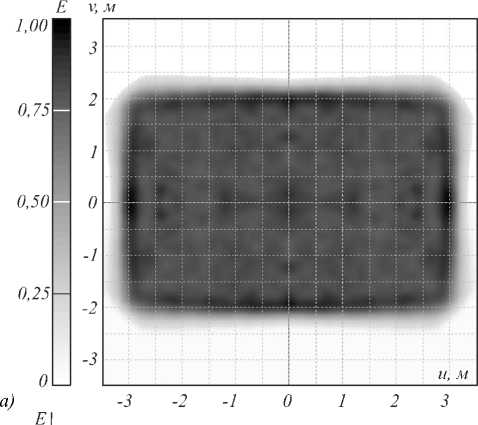
Представляют интерес характеристики работы зеркала при реальном протяжённом источнике. На рис. 7 представлены результаты моделирования зеркала при протяжённом источнике с размером 1×1 мм2, излучающем по закону Ламберта. Здесь и далее при моделировании протяжённый источник считается прозрачным и не препятствует распространению лучей. ОСКО полученного распределения (рис. 7) составляет 4,6 %, то есть увеличение размера источника привело к увеличению равномерности формируемого распределения. В то же время увеличение размера источника приводит к размытию границы освещаемой области. Таким образом, предложенный метод расчёта позволяет рассчитывать отра- жающие поверхности, которые имеют хорошие рабо- чие характеристики не только для точечного, но и для протяжённого источника излучения.

0,50

0,25

б)-4-2        0        2 н, v, л,

Рис. 7. Распределение освещённости, формируемое зеркалом при протяжённом источнике излучения с размерами 1×1мм2: полутоновое распределение освещённости (а); профили распределения освещённости (б)

Аналогичным образом была решена задача расчёта зеркала, формирующего равномерно освещённую эллиптическую область с длинами осей 6 м и 3 м в выходной плоскости, расположенной на расстоянии 10 м от точечного ламбертовского источника света. Методом согласованных квадрик были получены значения функции эйконала в узлах равномерной сетки, заданной с шагом 20 см по обеим координатным осям. При таком разбиении в формируемую эллиптическую область попали 455 точек. График функции эйконала на выходной плоскости представлен на рис. 8. Результаты моделирования работы восстановленной сегментированной поверхности в программе Trace Pro приведены на рис. 9 и показывают фокусировку в заданный набор точек.

Для восстановления поверхности зеркала (рис. 10), формирующего постоянную освещённость в эллиптической области, полученные значения функ- ции эйконала Ψi, i = 1,…,455, были аппроксимированы бикубическим сплайном на сетке с 6 патчами по оси Ox и 4 патчами по оси Oy.

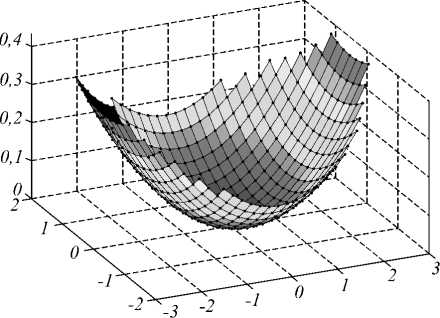
Рис. 8. Функция эйконала для фокусировки в набор точек в эллиптической области

Е v, м

и, м

• -3   -2-1 О 1    2   3

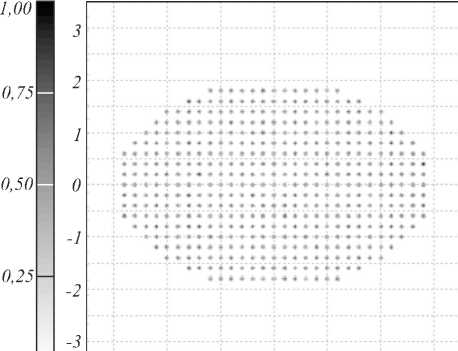
Рис. 9. Полутоновое распределение освещённости, формируемое сегментированным зеркалом для фокусировки в набор точек в эллиптической области

Результаты моделирования работы рассчитанной поверхности в программе Trace Pro с точечным ламбертовским источником излучения и протяжённым прозрачным источником излучения с размерами 1×1 мм2 приведены на рис. 11, 12 соответсвенно. ОСКО полученного светового распределения от равномерного составляет 5,9 % в случае точечного источника и 4,8 % в случае протяжённого источника с размером 1×1 мм2.

Аналогично предыдущим примерам было рассчитано зеркало (рис.13), формирующее равномерно освещённый равносторонний треугольник со стороной 6 м в выходной плоскости, расположенной на расстоянии 10 м от точечного ламбертовского источника света. Для этого методом согласованных квадрик были получены значения функции эйконала в узлах равномерной сетки, заданной с шагом 20 см (внутрь области попали 512 точек), которые затем были аппроксимированы бикубическим сплайном с 6 патчами по осям Ox и Oy .

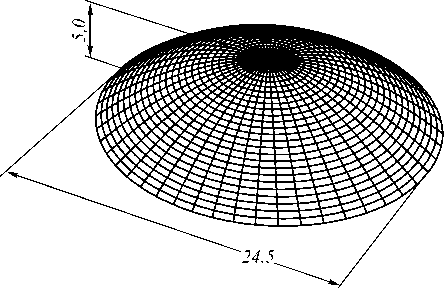
Рис. 10. Отражающая поверхность, формирующая равномерное распределение освещённости в эллиптической области (габаритные размеры зеркала указаны в мм)

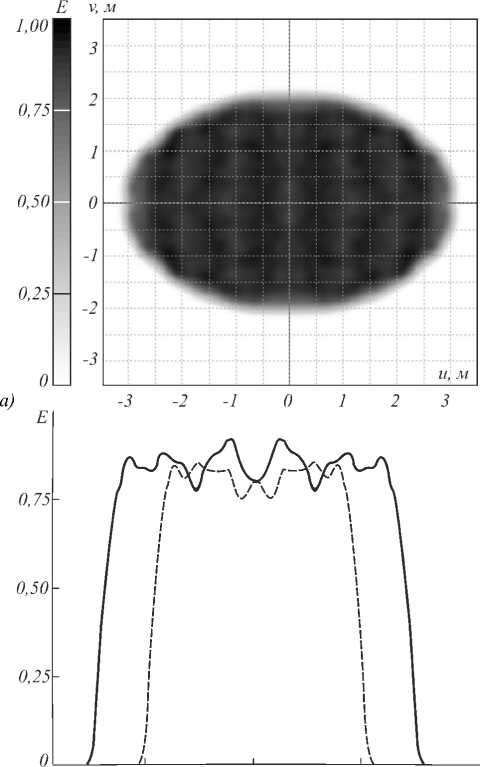
• б)     -4          -2               0               2 и, г; л/

Рис. 11. Полутоновое распределение освещённости, формируемое зеркалом для фокусировки в набор точек в эллиптической области для точечного распределения освещённости: полутоновое распределение освещённости (а); профили распределения освещённости (б)

По полученной непрерывной функции эйконала была восстановлена поверхность зеркала по формулам (5) и (6). Результаты моделирования работы рассчитанной поверхности в программе Trace Pro с точечным ламбертовским источником излучения и с протяжённым прозрачным источником излучения с размерами 1×1 мм2 приведены на рис. 14, 15 соответсвенно. ОСКО составляет 7,8 % в случае точечного источника и 9,7 % в случае протяжённого источника.

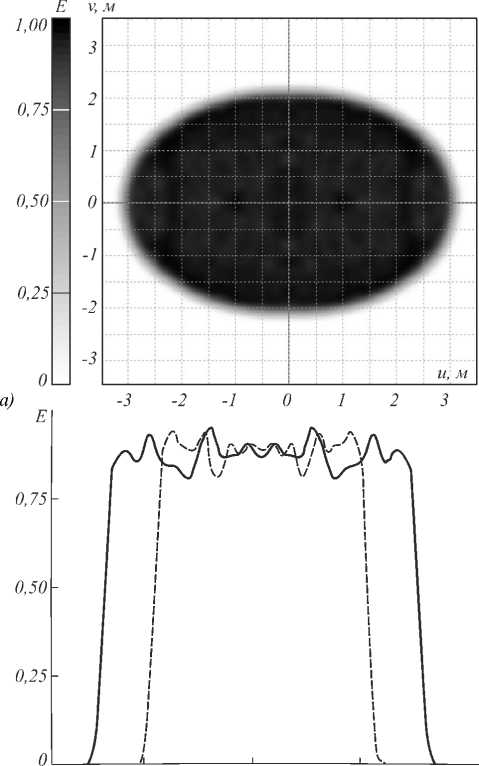
• б)     -4          -2               0              2 и, v, л/

Рис. 12. Полутоновое распределение освещённости, формируемое зеркалом для фокусировки в набор точек в эллиптической области для протяжённого источника с размерами 1×1 мм: полутоновое распределение освещённости (а); профили распределения освещённости (б)

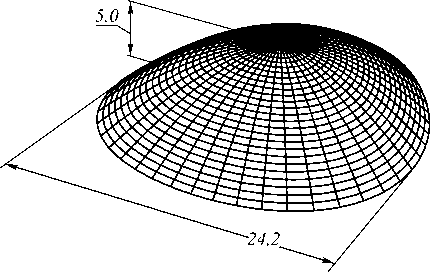
Рис. 13. Отражающая поверхность, формирующая равномерное распределение освещённости в треугольной области (габаритные размеры зеркала указаны в мм)

Вышеприведённые примеры демонстрируют хорошую работоспособность метода при формировании равномерных распределений освещённости в выпуклых областях. Рабочие характеристики метода при формировании более сложных световых распределений (например, при формировании световых распределений для дорожного освещения или равномерных распределений освещённости в двусвязных областях) являются предметом дальнейших исследований.

E v, м

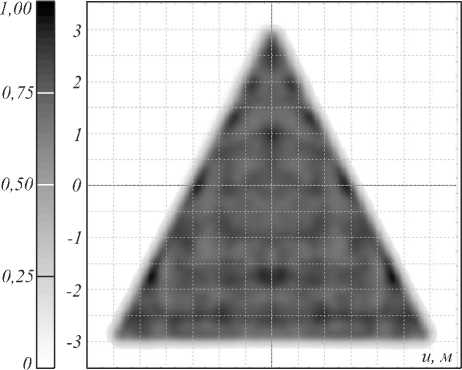
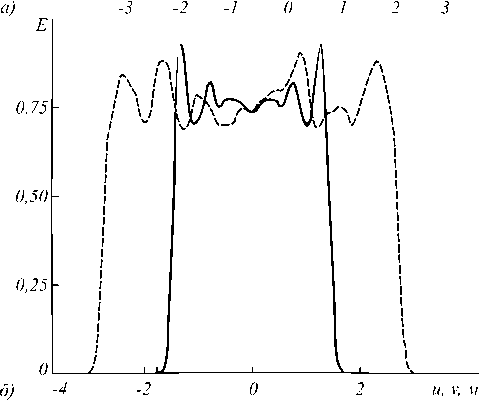
Рис. 14. Полутоновое распределение освещённости, формируемое зеркалом для фокусировки в набор точек в треугольной области для точечного распределения освещённости: полутоновое распределение освещённости (а); профили распределения освещённости (б)

Заключение

В работе предложен метод расчёта отражающей поверхности, формирующей заданное непрерывное распределение освещённости в двумерной области. В методе поверхность зеркала представляется в виде огибающей двухпараметрического семейства эллипсоидов. Такое представление поверхности является предельным случаем сегментированной поверхности, используемой в методе согласованных квадрик для фокусировки в набор точек (точки фокусировки расположены в узлах прямоугольной сетки, аппроксимирующей заданную область). Огибающая поверхность имеет простой ана- литический вид и зависит от функции, определяющей длины осей эллипсоидов семейства.

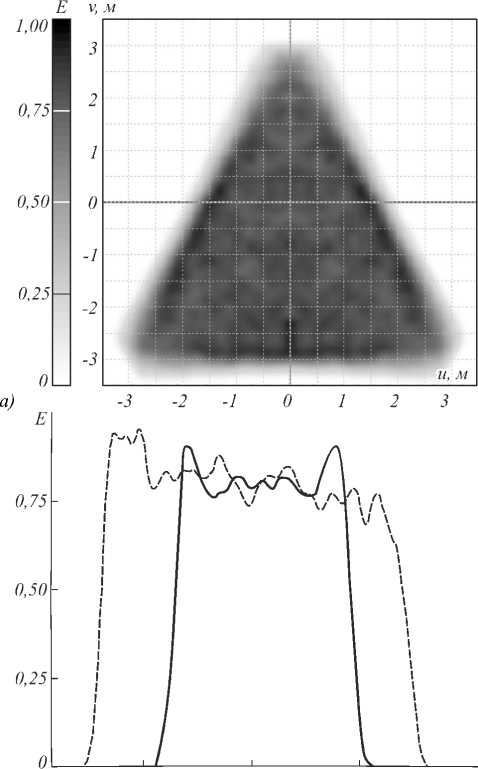
б)   -4-2        0        2 и, v, л/

Рис. 15. Полутоновое распределение освещённости, формируемое зеркалом для фокусировки в набор точек в треугольной области для протяжённого источника с размерами 1x1 мм: полутоновое распределение освещённости (а); профили распределения освещённости (б)

Данная функция соответствует эйконалу Ψ в области фокусировки и определяет распределение освещённости, формируемое в заданной области. Расчёт непрерывной функции Ψ осуществляется на основе непрерывной аппроксимации дискретной функции эйконала, полученной из решения дискретной задачи фокусировки в набор точек с помощью метода согласованных квадрик.

С использованием предложенного метода были рассчитаны зеркала, формирующие равномерные распределения освещённости в прямоугольной, эллиптической и треугольной областях. Результаты моделирования работы рассчитанных зеркал демонстрируют их высокие рабочие характеристики: относительное среднеквадратическое отклонение формируемого распределения освещённости от требуемого не превышает 8 % в случае точечного источника и 10 % в случае протяжённого источника с размерами

1×1 мм2. Исследование возможности формирования сложных невыпуклых областей будет предметом дальнейших исследований.

Исследование выполнено при поддержке Министерства образования и науки РФ, грантов РФФИ № 14-07-31135-мол_а, 14-07-00339-А, 13-07-97001-р_поволжье_а.