Расчёт железобетонных дымовых труб на основе диаграмм деформирования бетона и арматуры

В нормах проектирования дымовых труб [1, 2] в качестве расчётной схемы принимается защемлённый в основании консольный стержень кольцевого сечения. При этом изгибающие моменты определяются из расчёта по деформированной схеме (геометрическая нелинейность), а в железобетонных трубах кроме того учитываются образование трещин и снижение жёсткостных характеристик ствола трубы по сравнению с исходными (физическая нелинейность). Методика расчёта стволов дымовых труб в такой постановке была разработана ещё в середине прошлого века В.И. Мурашёвым [3] и легла в основу ряда инструктивных документов [2, 4, 5]. Поскольку методика В.И. Мурашёва ориентирована на расчёт «вручную», она использует упрощённые схемы работы сечений. В частности, после образования трещин не учитывается работа растянутого бетона, распределение напряжений в растянутой арматуре и сжатом бетоне принимается постоянным в пределах поперечного сечения ствола трубы.

Оставаясь в рамках требований нормативных документов по расчёту дымовых труб, расчётная модель может быть уточнена за счёт введения нелинейных диаграмм деформирования бетона и арматуры, рекомендованных сводом правил [6] (рис. 1).

Общие уравнения для расчёта железобетонного кольцевого сечения с использованием нелинейных диаграмм деформирования бетона и арматуры применительно к стержневым элементам были предложены С.Н. Карпенко [7]. В.И. Соломин [8], с использованием вариационно-разностного подхода, представил уравнения и алгоритм расчёта железобетонных стволов дымовых труб на основе нелинейной деформационной модели.

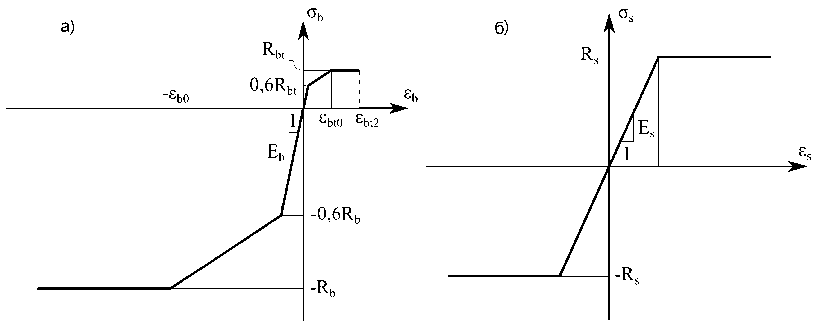
Рис. 1. Диаграммы деформирования бетона (а) и арматуры (б)

В данной статье показан способ и результаты расчётов стволов железобетонных дымовых труб с использованием диаграмм деформирования бетона и арматуры. Способ расчёта предполагает компьютерную реализацию и использование дискретных расчётных моделей сечения и ствола трубы.

Алгоритм «Сечение»

Кольцевое сечение разбивается по радиусу и окружности на n_b фрагментов бетона и n_s фрагментов арматуры (рис. 2).

В пределах каждого участка напряжения предполагаются равномерно распределёнными. В качестве обобщённых усилий принимаются продольная сила N и изгибающий момент M_x . В качестве обобщённых деформаций – кривизна æ_x и относительная деформация ε ₀ геометрической оси стержня. Связь между напряжениями и обобщёнными усилиями устанавливается уравнениями статической эквивалентности:

nbn

• N = Z ° b, i AAb, i + Z ° s, j AAs, j ,(1)

i=1

nbn

Mx = Z °b,iУь,iAAb,i + Z °s,j^s,jAAs,j ,(2)

i=1

где ° b i , ° s j — напряжения соответственно в i -м фрагменте бетона и j -м фрагменте арматуры;

A A b i , A A s , j - площадь соответственно i -го фрагмента бетона и j -го фрагмента арматуры;

• y_{b , i} , y_{s , j} – ордината соответственно i -го фрагмента бетона и j -го фрагмента арматуры.

Распределение деформаций принимается, считая справедливой гипотезу плоских сечений:

• £ = s о + yre_x ,                                   (3)

где 8 - относительная деформация волокон с координатой y .

Добавляя к (1)–(3) зависимости

° b =° b ^{( 8 ) и} ° s =° s ( ^{s )}, ⁽⁴⁾ вытекающие из принятых диаграмм деформирования бетона и арматуры, получаем замкнутую систему уравнений для расчёта сечения. При этом могут быть решены две задачи:

• - при заданных 8 ₀ и ^_х найти соответствующие значения N и M_x ;

• – при заданных N и M_x найти соответствующие значения 8 ₀ и ш_х .

Первая задача решается последовательным применением формул (3), (4), (1) и (2).

Вторая задача решается путём многократного решения первой задачи с целью подбора таких 8 0 и ^ x , при которых уравнения (1), (2) выполняются с необходимой точностью.

Алгоритмы решения этих задач в совокупности образуют расчётную модель железобетонного сечения.

Алгоритм «Ствол»

Расчёт ствола выполняется по деформированной схеме. При известном изгибе оси ствола усилия в нём определяются методом сечений, так как задача является статически определимой. Поскольку изгиб оси ствола зависит в том числе от нелинейных свойств материалов, задача решается путём последовательных приближений с уточнением на каждой итерации горизонтальных перемещений оси стержня и слагаемых изгибающих моментов в каждом сечении от собственного веса вышерасположенной части ствола.

Для численного решения ось ствола разбивается на участки и на границах участков вводятся узлы, в которых будет выполняться расчёт сечений. Нагрузки от собственного веса и давления ветра на участках прикладываются в соответст-

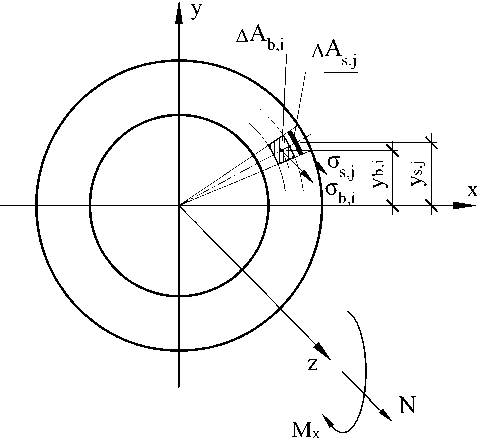
Рис. 2. Схема сечения с изображением фрагментов бетона и арматуры

вующих узлах. Расчётная схема ствола трубы изображена на рис. 3.

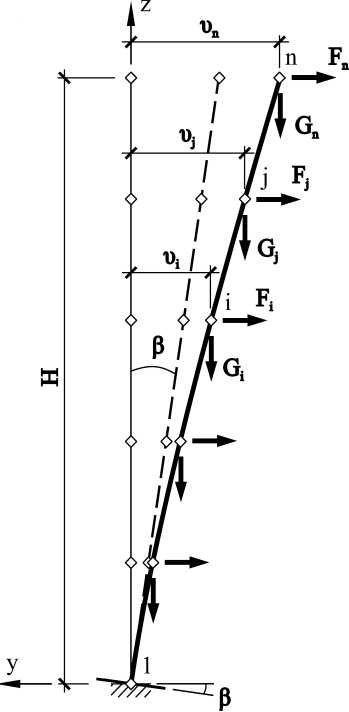
Рис. 3. Расчётная схема ствола железобетонной трубы

Изгибающие моменты в каждом сечении вычисляются по формуле: n

M x,i = M x0,i + Y G j (. » j -» i) ,             (5)

j = i + 1

где M_{x 0, i} – слагаемое изгибающего момента, вызванное горизонтальными нагрузками.

Второе слагаемое в (5) обусловлено деформируемостью расчётной схемы и определяется путём последовательных приближений. Продольные силы при этом являются неизменными.

При известных изгибающих моментах и продольных силах с помощью алгоритма «Сечение» находятся кривизны æ_x,i в каждом узле стержня. Далее, пользуясь связью кривизн, углов поворота и перемещений ( ш = О’ = и") с учётом граничных условий и 1 = 0, О 1 = Р , путём последовательного численного интегрирования определяются углы поворота О i и перемещения и i в каждом узле.

Последовательное применение внешнего алгоритма «Ствол» и внутреннего алгоритма «Сече- ние» завершается при достижении необходимой точности расчёта.

Компьютерная реализация

На языке программирования Python авторами была разработана компьютерная программа, которая прошла тщательное тестирование как на уровнях алгоритмов «Сечение» и «Ствол», так и при их совокупной работе. В качестве таких тестовых примеров использовались задачи, имевшие аналитическое решение. Исследовалось также влияние дискретизации объекта (разбивки сечений на фрагменты и стержня на участки) на результаты расчёта.

Примеры расчётов

В исследовательских целях для условной цилиндрической трубы высотой 60 м была проведена серия расчётов как по существующему [2], так и по предлагаемому методам. Цель – выявить возможные расхождения в получаемых результатах и найти их причину.

Для этого по [2, 9] были определены действующие на трубу расчётные ветровые нагрузки. Затем была произведена серия расчётов для разных уровней ветрового давления. Базовое ветровое давление, определённое для II ветрового района, на каждом из участков умножалось на коэффициент k. Исследовался диапазон k = 0,5…2,0 (50%…200%). Нагрузка от собственного веса оставалась неизменной. Крен трубы принимался равным нулю. Результаты расчётов в виде эпюр приведены на рис. 4–6. Пунктирной линией на рис. 4–6 обозначены уровни образования трещин, т. е. в сечениях ниже данного уровня при расчёте выявлено образование горизонтальных трещин. Различия в уровнях обусловлены, в частности, тем, что при расчёте по существующему методу работа растянутого бетона не учитывается. В качестве критерия трещинообразования при расчёте по предлагаемому способу принято достижение в наиболее растянутом волокне бетона деформации ε bt2 (см. рис. 1).

Расчёты показали следующее:

• 1.    При k = 0,5 в обоих случаях конструкция работает в линейно-упругой стадии. Однако при этом прогибы и кривизны отличаются, что связано с различными начальными значениями изгибных жёсткостей.

• 2.    При появлении трещин в расчёте по существующему методу наблюдается резкий скачок на эпюре кривизн (до 7–8 раз). Скачок на эпюрах кривизн по предлагаемому способу не столь значительный (увеличение кривизны примерно в 2 раза).

• 3.    При расчёте по существующему методу геометрическая нелинейность проявляется в значительно большей степени, чем по предлагаемому методу. Отсюда вытекают различия в значениях изгибающих моментов при k > 0,5.

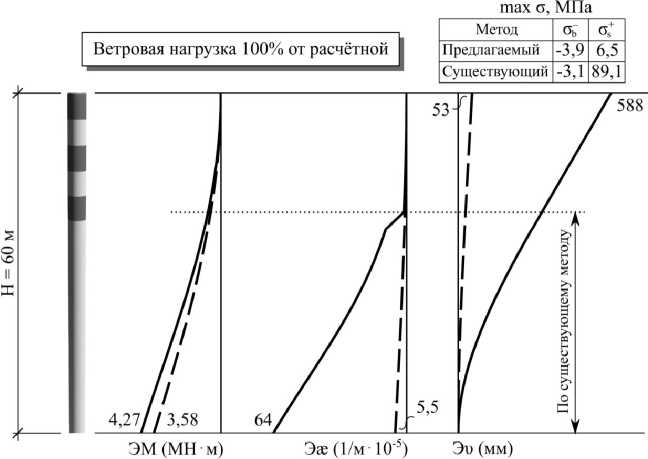
Рис. 4. Результаты расчёта цилиндрической трубы при k = 0,5: сплошной линией обозначены эпюры по результатам расчётов по существующему методу, штриховой линией – по предлагаемому методу

Рис. 5. Результаты расчёта цилиндрической трубы при k = 1,0: обозначения см. на рис. 4

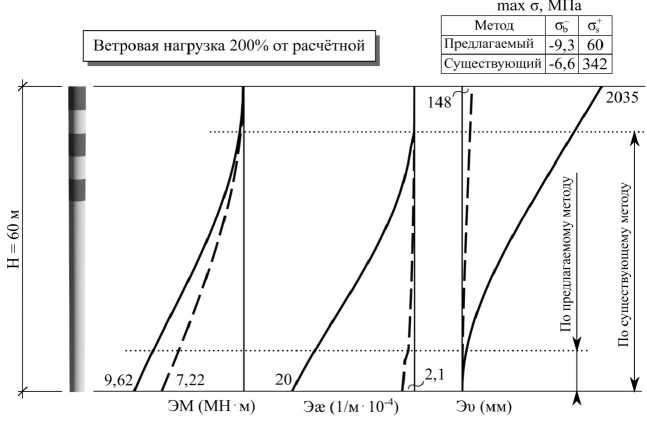
Рис. 6. Результаты расчёта цилиндрической трубы при k = 2,0: обозначения см. на рис. 4

Выводы

Методика расчёта железобетонных дымовых труб, заложенная в нормативных документах [2, 4, 5], далека от совершенства. Предлагаемый способ расчёта позволяет освободиться от ряда упрощающих предпосылок, дать более достоверное распределение напряжений в сечении, учесть работу растянутого бетона, точнее описать процессы деформирования.

При дальнейшем развитии этого способа и компьютерной программы несложно учесть проёмы в стволе трубы, неоднородность свойств материалов по высоте трубы и по площади сечений, что представляет большую ценность при проектировании и поверочных расчётах реальных объектов.