Расчётная модель двухслойного пористого подшипника конечной длины с учётом анизотропии пористых слоёв и нелинейных факторов

Для расчёта двухслойных пористых подшипников, работающих под давлением питания, необходимо представить коэффициент проницаемости в виде непрерывной функции, зависящей от радиальной и окружной координат. Однако учёт анизотропии только лишь в окружном направлении [3, 4] не позволяет представить коэффициент непроницаемости таким образом. Ниже нами приводится решение рассматриваемой задачи в нелинейной постановке при учете зависимости проницаемости пористых слоёв от радиальной и окружной координат.

Постановка задачи. Рассматривается установившееся течение вязкой несжимаемой жидкости в зазоре двухслойного пористого радиального подшипника конечной длины. Подшипник с неоднородным пористым слоем на его поверхности считается неподвижным, а шип вращается с угловой скоростью Ω. Смазка в зазор пористого подшипника переменной проницаемости в осевом направ- лении подается под давлением питания.

Поместим начало цилиндрической системы координат r , θ, z на оси подшипника на равном расстоянии l от его концов (1).

Тогда уравнения контуров шипа и подшипника можно записать в виде c1 : r = b, c 2: r = b + h1, c 3: r = b + h, h = h2 - h1, c 0: r = a-(1 + H), H = Ecos9 - 2E2sin26,

где h — толщина пористого слоя; а — радиус шипа; b — радиус подшипника; е = e; е — a эксцентриситет.

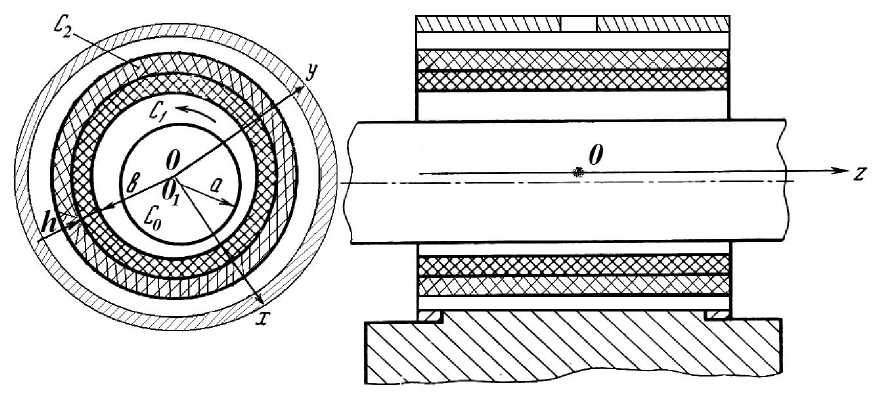
Рис. 1. Схематическое изображение радиального подшипника с многослойным пористым вкладышем и пористым шипом

Проницаемости пористых слоёв зададим таким образом, чтобы на границе раздела пористых слоёв они принимали одинаковые значения rr к' = Ae 1      + к (0), к2 = Ae 2 h + к (0).                            (2)

Здесь A — заданная постоянная величина; безразмерные параметры Л_т >  0 и Х 2 >  0 характеризуют распределение проницаемостей пористых слоёв в радиальном направлении. Функцию к ( 0 ) по аналогии с законом изменения формы смазочной плёнки зададим в виде к = — A cos0, где

Д']A = е * <  1. Также предполагается, что е * и е — малые параметры одного порядка е = п * е * .

Основные уравнения и граничные условия. Будем исходить из безразмерных уравнений движения вязкой несжимаемой жидкости в смазочном слое и в том числе в пористых слоях вкладыша, а также из уравнения неразрывности.

Re

d u U д и      ди_

U —r + ^{0  0} + U z

^Г дГ Г д 0     z дz

—

υ 2 _θ r

Re

д и_А U д и    д и ии

θ       θ θ           θ       r θ

--1----+ и_--- дГ   Г д9 z дz    Г

1 др д ² и _Г 1 д и _Г 1 д ² и _Г д ² и _Г _и2__ 2 д и ₀

( 1 _{— а} ) ² д Г ⁺ д Г ^{2 +} г дГ ⁺ г ² д 0 ^{2 +} д z ² г ² г ² д 0 , 1     1 д р , ^д2^и0 , 1 ^{д и}0 , 1 ^д 2^и0 , ^д2^и0 ^и0 , 2 ^{д и} г

--------^---— +-- Т- +----1--^-- "V +----- Т +--^--,

( 1 _{— а} ) ² г д 0    д г ²    г дг   Г ² д 0 ²     д z ² г ² г ² д9

Re	д и_   U д и_      д и7 и - z + -0 - z + U7 - z	1     д р  д 2 и    1 д и.   1 д2ш   д 2 и7 =--т—+ — z +-- z + —г — z + — z ,
	rz	(1-а)2 д z д г 2 г дг г 2 д02   д z 2

	д и Г	1 + —	д и   д и7 —0 + — z +		υ r	= 0	,
	д г	r	д 0	д z	r
к1 ( Г , 0 ) '	д 2 Ф 1 д Ф	1	д 2 Ф	д 2 Ф "		д к ,	д Ф	1 д к	д Ф	= 0,
			д 0 2					+-- 1
	д г 2 Г дг	Г 2		д z 2 _		д г	дг	г д 0	д 0
к 2 ( r ,e ) .	"д 2 F 1 д F	1	д 2 F	д 2 F 1		д к 2	дF	1 д к 2	дF	= 0.
			д 0 2		+
	_д г 2 г дг	Г 2		д z 2 J		дг	дг	г д 0	д 0

Здесь υ _r , υ _z , υ_θ — безразмерные компоненты вектора скорости; p — безразмерное гидродинамическое давление в смазочном слое; Φ и F — соответственно безразмерные гидродинамические давления в пористых слоях; k ₁ и k ₂ — безразмерные проницаемости пористых слоёв.

Размерные величины r, z, ur, u8,uz, P, Ф, F и к’ k2 связаны с безразмерными r , z, Ur, U8,Uz, P, Ф, F , k1, k2 соотношениями r = br , z = 1Z, к/ = Ak, k2 Ak2, ur = Qsu r, u8 = Qsu8

P = ^Q ab p _ф = ^Q ab ф   F = ^Q ab f                      (4)

( b - a ) ²           b ^- a b ^- a

В дальнейшем знак ~ у безразмерных переменных опускается.

Система уравнений (3) решается при следующих граничных условиях.

• 1.    На контуре с выполняется непрерывность давлений ( P = Ф ) , а компонента вектора

• 2.    На границе раздела пористых слоёв

• 3.    F r = b + h = P g , где P g — закон подачи смазки.

• 4.    На контуре с₁ при z = ± у давление равно p_A , где p_A = p_a/p* .

• 5.    На поверхности шипа выполняются следующие условия:

скорости υ _r определяется законом Дарси. Остальные компоненты равны нулю.

, дФ , d F

Ф = f , к — = k — .

• I    a H + ... = - Esin8, r = a

  
  

| a H + — = 1, r = a

(              I      Г dw)               _ w (a + aH ) = w +— aH + ... = 0.

• ^V                    I r =a    I _5f I

V      J r =a

Асимптотическое решение задачи. Установив закон подачи смазки как

x pg = c (z2 - у2) + £(an cos8 + bn sin8)en,                            (6)

n = 1

решение системы (3), удовлетворяющее выше приведённым граничным условиям, будем искать в виде:

p = A - ( z ² - у² ) + p a + P ( r ,8 ) , Ф = N • ( z ² - у² ) + p a + R i ( r ,8 ) , F = N • ( z ² - у² ) + p a + R ₂ ( r ,8 ) , u r = u ( r ,8 ) , U 8 = v ( r ,8 ) , U z = w ( r ,8 ) z

Исходя из вида граничных условий функции P , R , Ф, u (r,8), u (r,8) w (r,8) будем искать в виде рядов по степеням параметра ε :

P = P0 (r ) + EP1 (ri,8) + - , Ri = Ф0 (r ) + ЕФ1 (ri,8) + - , R2 = F0 (r) + EF1 (ri,8) + -, u = u0 (r) + eu1 (r,8) + —, u = u0 (r) + eu1 (r,8) + —, w = w0 (r) + ew1 (r,8) + —

Для определения коэффициентов разложений (8) с точностью до членов О (ε²) придём к следующей системе уравнений и граничных условий к ним:

, ^du 0 - Ц. 1 = - 1 dp 0 ₊ d 2 ^u 0 ₊ 1 ^du 0 - u 0 ⁰ dr r J ( ₁ - _a ) ² dr dr ² r dr r ² ,

, ^{d u}0 ₊ ^u 0^u0 1 = ^d 2^u0 ₊ 1 ^{d u}0 - u 0

⁰ dr r dr ² r dr r ² ,

Г dw ?

Re ^u 0 dr ⁺ w 0

du u     d ² Φ

⁰ + w +   = 0 ,     7⁰

dr ⁰ r dr ²

n du du

Re и —¹ + и —° +

⁰ dr ¹ dr

^u0 и r d e

—

—

2 A

^{( 1 — a ) 2}

d ² w  1 dw

+---Л +--0, dr2 r dr

λ 1 d Φ 0 d ² F 0

₊ 1 ^{d Ф} 0 , r dr r dr ^, dr

d ² N

dr ²

1 dN r dr

—

4 N = 0 . γ²

₊ 1 ^dF o r dr

о      du,       d u_n

Re и —¹ + и —° +

⁰ dr ¹ dr

2υ₀υ₁ r

—

5P i

( 1 — a ) ^{2 d r}

d^ _  ±

+ —1- + —1 + dr2   r dr

1 дu

^uo d U 1 ₊ ^u 1^uo + u o^u1

r d e

Re

—

r

dw    dw.

и —¹ + и —⁰ + 01

1 dp₁ d ² u₁ 1 d u₁ ( 1 _{— a} ) ² r d e    d r ²    r dr

λ 2 dF 0

,

r dr ,

1 d 2 u 1

r 2 d e 2

1 d 2 u

- + —, —

—

— u1 r2

r ² de^:

2 d u₁

r ² ae '

4+ r ²

2 du₁ r ² de '

^u0 w r d e

d ² w  1 d w   1 d ² w

----1 +---1 +---1

dr ²     r dr    r ² d e ² '

ди   1 d u    и _n d ²ф,   1 д Ф,   1 d ² Ф₁

¹ + з! +   = 0,        + ¹ +      т¹

dr   r d e     r        dr ²     r dr   r ² d e ²

A₁ д Ф₁

■7 "d r"'

d 2F   1 dF   1 d 2F    A2

-----T--1----1--T--T- =.

dr2   r dr   r2 de2      rd

Граничные условия запишем в виде:

и 0 ( a ) = 0, U 0 ( a ) = 1, w 0 ( a ) = 0, N ( 1 ) = A, N ' ( 1 ) = 0,

и 0 ( 1 ) = - ф ( 1 — a ) Ф 0 ( 1 ) , U 0 ( 1 ) = 0, ^w 0 ( 1 ) = ^— Ф ( 1 - ^a ) , Ф 0 ( 1 ) = P 0 ( 1 ) , Ф 0 ( в 1 ) = F 0 ( в 1 ) , Ф 0 ( в 1 ) = ^ > ' ( в ! ) , Ф 0 ( в 2 ) = P^Qg— P a , N ( в 2 ) = c , и ₁ ( a,e ) = — sine, u₁ ( a,e ) = — u 0 ( a ) acose, w ₁ ( a,e ) = — w 0 ( a ) acose,

^w 1 ( ^1,e ) = ⁰ , и ( l,a ) = ^— ф ( 1 ^{— a} ) | r

+ ф ( 1 — a ) Ф 0 ( 1 ) n * cose, r = 1

U 1 ( 1,a ) = — ф ( 1 — a )^ , P 1 ( 1,e ) = Ф 1 ( 1,e ) = 0, F 1 ( p 2 ,e ) = 5 1 cose + / ^sine, d e

Ф 1 ( P 1 ,e ) = F 1 ( P 1 ,6 ) , Ф ; ( в 1 ,e ) = F 1 ' ( P 1 ,e ) .

h             h         Ab     ^λ 1 ^{ln b}

Здесь Pi = 1 + -1 , в₂ = 1 + т-, Ф =-------- г' e ^{b +} h ¹ .

b            ^b       ( b — a ) 3

Исходя из вида граничных условий, решение системы (10) для первого приближения будем искать в виде:

и ₁ = и ₁₁ ( r ) cose + и ₁₂ ( r ) sine, u₁ = u₁₁ ( r ) cose + u₁₂ ( r ) sine, w ₁ = w ₁₁ ( r ) cose + w ₁₂ ( r ) sine, P ₁ = P ₁₁ ( r ) cose + P ₁₂ ( r ) sine, и ₁ = и ₁₁ ( r ) cose + и ₁₂ ( r ) sine, Ф₁ = Ф₁₁ ( r ) cose + Ф₁₂ ( r ) sine, F₁ = F ₁₁ ( r ) cose + F ₁₂ ( r ) sine.

Подставляя выражение (13) в уравнения (10) и граничные условия (12), получим:

^и 11 ⁺ r ^и 11

—

2 r 2 u 11

—

_r2 ^u12 =         .2

^{r ( 1 — a )}

un p-ц+Reи0и'ц+и0ип+-0g-и12

—

2υ

0υ r 11

,

^U 12 ^{+ 1 U} 12

—

2 r 2 u 12

—

^υ r ²

11    /1      \2

^{( 1 — a )}

P 2 + Re uu + u 0 u

0 u 12

0 u 12

—

υ

0u r 11

—

2υ

0υ r 12

,

^u11 ⁺ r ^U11

—

2 r 2^υ11

+--r U .2 ^— -------2

^r 2        ( 1 — a ) ²

1 „ n

0P 12 + Re u o^u ‘ 1 + u 0^U

0 υ 11

0 υ 11

υ

+ — U2

r 12

u υ

⁺ -yUn ⁺ -07 ^U 11

,

^U12 ^{+ 1u}12

—

2 r ^{2 υ12}

—

_r 2 ^u 11 ~

—

^{( 1 — a ) 2}

1 „ n

0P 11 + Re u o^u ‘ 2 + ^u>

0 υ 12

12 υ 0

—

υ

0υ r 11

u υ

⁺ yU₁₂ + -0- ^U 12

,

wn ⁺ yw n ^— 0 2 w 11

= ^R e ^u₀W^ + w 0 ^u 11

υ

+—w r 12

w 12 ^{+ 1} w 12 ^— 00 2 w 12 = ^R e

υ

^U 0 w 12 ⁺ w 0 ^U 12 ⁺ -0" w 11 ^{+ 2} w 0 w 1

u" + 1U 12 +   = 0, U 2 — 1u_n + Ц ¹ = 0 ,

1         1 λ₁               1         1           λ ₂

^Ф11 ⁺ r ^Ф11 r 2 ^Ф11 r ^ф1 , ^Ф12 + r ^Ф12    r 2 ^Ф12      r ^Ф1

^U 11 ( ^a ) = ⁰, ^u 12 ( ^a ) = ^—1, Un ( a ) = ^—u 0 ( a ) a, ^u12 ( ^a ) = ⁰ , ^w 11 ( ^a ) = ^— w 0 ( ^a ) ^a , ^w 12 ( ^a ) = ⁰ ,

^U 11 ( 1 ) = ^— ф ( 1 ^{— a} ) ^ф11 ( 1 ) ^— ( 1 ^{— a} ) ^U 0 ( 1 ) П * , ^u 12 ( 1 ) = ^— ф ( 1 ^{— a} ) ^ф12 ( 1 ) , ^u11 ( 1 ) = ^— ф ( 1 ^{— a} ) ^ф12 ( 1 ) , ^u12 ( 1 ) = ^— ф ( 1 ^{— a} ) ^Ф11 ( 1 ) , W 11 ( 1 ) = 0, W 12 ( 1 ) = 0, P 11 ( 1 ) = 0, P 12 ( 1 ) = 0, Ф 11 ( 1 ) = 0, Ф 12 ( 1 ) = 0, F 11 ( в 2 ) = a 1 , F 12 ( P a ) = b 1 ,

F 11 ( P 1 ) = Ф 11 ( в 1 ) ,    F 12 ( в 1 ) = Ф 12 ( в 1 ) ,    F 11 ( в 1 ) = Ф 11 ( в 1 ) ,    F 12 ( в 1 ) = Ф 12 ( в 1 ) .          (15)

Заменяя в выражениях (9), (11), (14) и (15) производные слагаемые конечноразностными пред- ставлениями, получим систему алгебраических уравнений, которая решается методом Гаусса — Зейделя.

Определение основных рабочих характеристик подшипника. Определив поле скоростей и давлений в смазочном слое, можно перейти к определению основных рабочих характеристик подшипника. Для составляющих вектора поддерживающей силы Rx и Ry, а также для момента трения получим следующие выражения:

R

x

™ab^Р 11 ( a ) , R y = ^nY^ a ^ b ? ^P 12 ( a ) , ( b — a )                     ( b — a )

M тр

a ³ μΩγπ l b

^u0 ( ^a ) ^—

^u0 ( ^a ) a

Основными рабочими характеристиками рассматриваемого подшипника являются: коэффициент нагруженности ς, коэффициент сопротивления вращению ξ, коэффициент трения f . Они определяются по формулам:

. = У 120 1 , N = / R T^ R T , ₅ = Myoi , f_ = 7 2 la pQ                 y       2 la ² p?    1 — a ^

Кроме того, параметрами рассматриваемого пористого подшипника, влияющими на его работоспособность, являются:

— постоянная проницаемость стенки вкладыша, прилегающей к смазочному слою (характеризуется параметром ψ);

— радиальный относительный эксцентриситет е =

e b - a '

— параметр η ε, обусловленный переменной составляющей проницаемости в окружном направ- лении;

b + h

— толщина вкладыша, характеризуемая безразмерной величиной в? =----;

2 b

h

— отношение толщины пористых слоёв ² ; h ₁

• —    длина подшипника 1 , характеризуемая безразмерным параметром y = —;

b

• —    параметры p_g ⁰ , p _a , a ₁, b ₁, обусловленные наличием давления питания;

• —    число Рейнольдса (Re);

— параметры λ 1 и λ 2 , характеризующие распределение давления в радиальном направлении в пористых слоях.

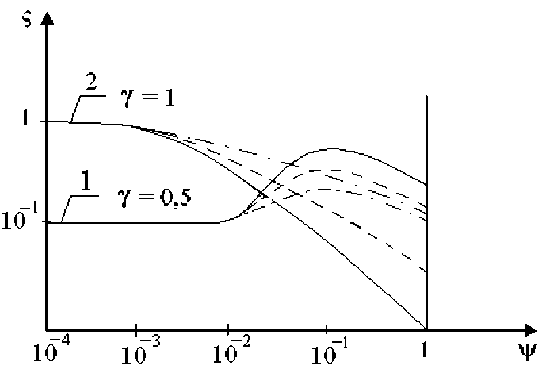
Рис. 2. Зависимость коэффициента нагруженности от параметра ф: Л 1 = Л ₂ = 0 ; а = 0,998 ; p g - p a = 0,5 ; в 2 = 1,6;

1 — γ = 0,5; 2 — γ = 1; сплошная линия — β 1 = 1,1; пунктир — β 1 = 1,2; пунктир с точкой — β 1 = 1,4

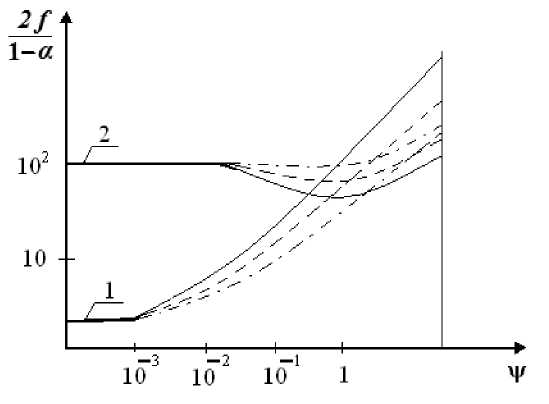
Рис. 3. Зависимость коэффициента трения от параметра ф: Л 1 = Л ₂ = 0 ; а = 0,998 ; p g - p a = 0,5 ; в 2 = 1,6;

1 — γ = 2; 2 — γ = 0,5; сплошная линия — β 1 = 1,1; пунктир — β 1 = 1,2; пунктир с точкой — β 1 = 1,4

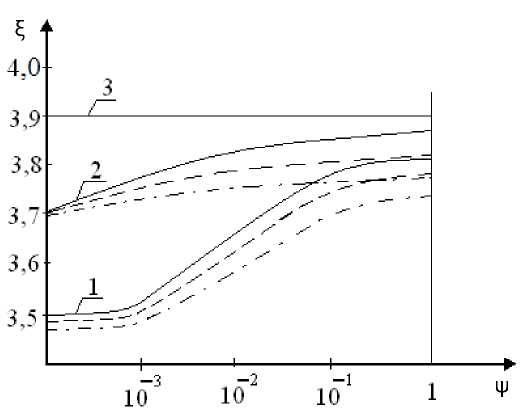
Рис. 4. Зависимость коэффициента сопротивления от коэффициента проницаемости: Л 1 = Л ₂ = 0 ; а = 0,998 ;

p g - p a = 0,5 ; в ₂ = 1,6; 1 — у = 2; 2 — У = 1; 3 — У = 0,5; сплошная линия — в 1 = 1,1; пунктир — в 1 = 1,2;

пунктир с точкой — β 1 = 1,4

Заключение. Результаты численного анализа, приведённые на рис. 2‒4, показывают следующее.

• 1.    При значении параметра Е = е, т. е. в случае, если проницаемость пористого слоя по окружности меняется по тому же закону, что и форма смазочной плёнки, подшипник по несущей способности обладает свойством подшипника двойного действия.

• 2.    При Л 1 = Л₂ = 0, т. е. в случае однослойного однородного пористого вкладыша в зависимости коэффициента нагруженности от параметра с при значениях у ^ 1 наблюдается ярко выраженный максимум при ф « 10 ^{- 1}.

• 3.    При Л 1 = Л₂ = 0 и у ^ 1 с увеличением значения параметра ф значение коэффициента нагруженности уменьшается. Наиболее резкое снижение значения коэффициента нагруженности наблюдается при ф « 10 ^{- 3}.

• 4.    При Л 1 = Л₂ = 0, у е [1; 2] с увеличением значения параметра ф значение коэффициента трения увеличивается. При этом резкое увеличение коэффициента трения имеет место при значениях ψ ≥ 10^-3. При значениях ψ < 10^-3 коэффициент трения практически остается постоянным с увеличением параметра ψ.

• 5.    При Л 1 = Л₂ = 0; у = 0,5; в е [1,1; 1,2] в зависимости коэффициента трения от параметра ψ наблюдается ярко выраженный минимум при ψ ≈ 1.

• 6.    Расчеты показывают, что при Л 1 * Л₂, т. е. в случае двухслойного пористого подшипника, при значениях — <  1 и h ² >  1 подшипник обладает более высокой несущей способностью, λ₁          h ₁

• 7.    Приведённые выше (в пунктах 1‒5) выводы остаются в силе и при λ 1 ≠ λ 2 , т. е. и в случае пористого двухслойного подшипника при непрерывном изменении проницаемости пористых слоёв в окружном и радиальном направлениях.

λh чем при 2 > 1 и 2 < 1.

λ₁          h ₁

Таким образом, на основании вышеизложенного можно сделать следующий вывод. При учёте анизотропии проницаемости пористых слоёв в окружном и радиальном направлениях можно обеспечить повышенную несущую способность подшипника при достаточно низком значении коэффициента трения.