Расчётная оценка эффективности демпфера сухого трения для полой широкохордной лопатки вентилятора

Бессчетнов Вадим Андреевич, начальник бригады перспективных методов анализа динамики и прочности трения), вследствие чего контактирующая область может иметь различный статус: прилипание, скольжение, зазор (нет контакта). Современные расчётные пакеты позволяют учесть нелинейное контактное взаимодействие элементов, однако контактные задачи, в которых рассматриваются вынужденные или затухающие колебания, по-прежнему требуют большого вычислительного ресурса. Поэтому в работе основной упор сделан на методы, позволяющие за короткий промежуток времени оценить демпфирующую эффективность конструкции, при этом, не нарушив качества расчётного результата.

Для оценки эффективности демпфирования и анализа работы демпфера при колебаниях лопатки был проведён ряд расчётов в конечноэлементном пакете ANSYS. На первом этапе расчетное исследование проходило на тестовой задаче: движение частицы по шероховатой поверхности под действием гармонически изменяющейся нагрузки (рис. 2а). Гармоническая нагрузка действовала на платформу в виде жёстких перемещений по синусоидальному закону, между частицей и платформой был задан стандартный контакт с коэффициентом трения ( k ). На частицу действовало ускорение свободного падения.

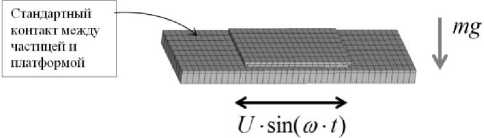
Рис. 2. Конечно-элементная модель и граничные условия

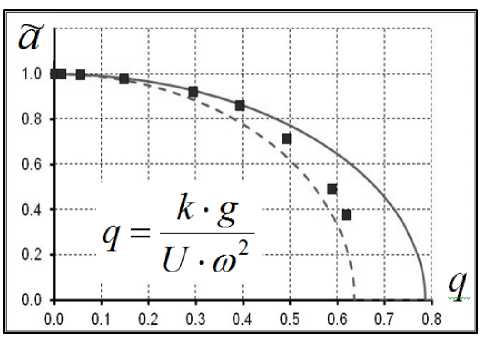
Результат расчета в ANSYS сравнивался с известными аналитическими решениями [1, 4], полученными методами гармонического баланса и точным решением (рис. 3а). Решение методом гармонического баланса основывалось на приближении по первой гармонике. Рассматривалась зависимость относительного перемещения частицы от безразмерного параметра :

∙

∙         ^,

где – коэффициент сухого трения; – ускорение свободного падения; – амплитуда перемещений платформы; – частота перемещений платформы.

=

Кубика

,

где _Кубика – амплитуда перемещения частицы.

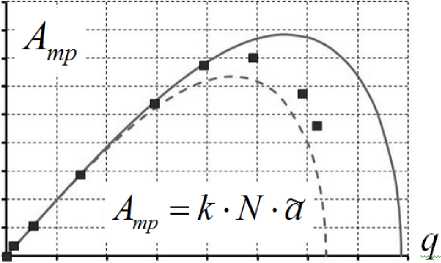
На поверхностях трения в процессе колебаний будет реализовываться проскальзывание частицы относительно платформы, и за счёт работы сил трения будет происходить потеря энергии колебаний. Работа силы трения между поверхностями зависит от величины проскальзывания и нормального усилия и вычисляется по формуле:

тр = ∙ ∙∆ , (3)

где _тр – работа силы трения; – нормальное усилие; Δ – величина проскальзывания.

Из уравнения (3) видно, чем выше нормальное усилие, тем выше работа силы трения. На рис. 3б изображена зависимость работы силы трения от параметра . Анализ сравнения результатов показал следующее:

• -    получена качественная сходимость результатов расчёта в ANSYS и точного решения;

• -    в области q~ 0-0,3 наблюдается качественная сходимость решения методом гармонического баланса с численным решением и точным решением. При этом расчёт методом гармонического баланса был основан на приближении по первой гармонике;

• -    в области q~ 0-0,45 движение частицы в численном расчёте описывается синусоидальным законом движения (параметры и имеют малое влияние) согласно методу гармонического баланса. В этой области прилипание частицы не осуществляется;

• -    в области q> 0,45 наблюдается расхождение численного решения с решением методом гармонического баланса. Расхождение объясняется наличием зон простаивания (слипания) частицы;

0.0    0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8

а)

б)

Рис. 3. а) график зависимости относительных перемещений кубика от параметра q; б) график зависимости работы силы трения от параметра q.

Сплошная линия – решение методом гармонического баланса; штриховая линия – точное решение; точки – численное решение в ANSYS

На втором этапе проводились расчёты собственных форм и частот колебаний лопатки с демпфером-имитатором. В данном расчёте анализировалось влияние демпфера на форму колебаний лопатки. По результатам тензометрирования лопатки было выявлено, что максимальные динамические напряжения имеют место по двум формам колебаний – первая и вторая изгибные формы. Дальнейшее расчётное исследование проводилось по двум формам колебаний. Несмотря на наличие нелинейностей (наличие контактной зоны с трением), установившиеся колебания в системе лопатка-демпфер должны оказаться близкими к гармоническим и описываться в первом приближении синусоидой. Предположение принято на основе удовлетворительной сходимости решения метода гармонического баланса с численным и точным решением.

Для экспресс-оценки эффективности прижимного демпфера был разработан следующий расчётный метод. Для воспроизведения влияния демпфера на лопатку достаточно было использовать невесомый демпфер-имитатор. Путём варьирования жёсткости имитатора, воспроизводилось давление демпфера на лопатку: малая жёсткость имитатора не влияла на форму колебаний, большая жёсткость имитатора приводила к заклиниванию лопатки в зоне контакта. Между демпфером-имитатором и лопаткой задавался контакт без возможности проскальзывания. На рис. 4 показаны граничные условия, центробежная нагрузка учитывалась. По результатам расчёта в зоне контакта из касательной реакции вычислялась сила трения _тр . Через силу трения высчитывалась работа силы трения, совершённая за один период колебаний. Затраченную работу силы трения переводили в логарифмический декремент колебаний через кинетическую энергию лопатки по формуле:

= ^{∑ тр} ∙ 100%,              (4)

кин где 5 - логарифмический декремент колебаний (%), Е Лтр - суммарная работа силы трения, совершённая за один период колебания, И4 ин - кинетическая энергия лопатки.

Результаты расчёта представлены на рис. 5. Каждая расчётная точка представляет собой расчёт собственных форм колебаний с определённой жесткостью демпфера-имитатора.

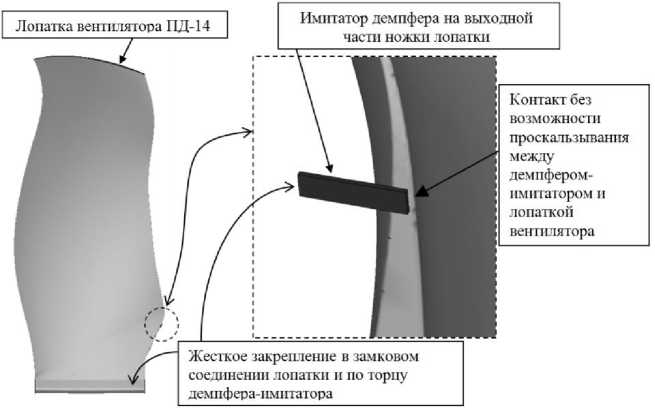
Рис. 4. Граничные условия при расчёте собственных форм и частот колебаний

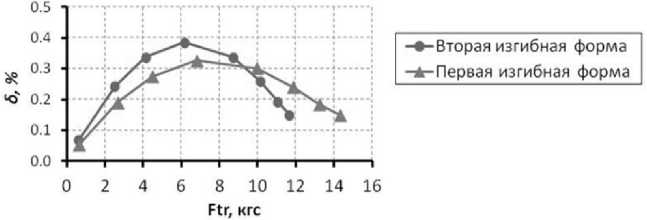
Рис. 5. Зависимость логарифмического декремента колебаний от силы трения по двум формам колебаний

Анализ результатов показал следующее:

• -    максимальный декремент колебаний от ~0,25 до 0,4 % достигается при значении силы трения от ~4 до 10 кгс по двум формам колебаний;

• -    сила прижатия демпфера имеет оптимальное значение, она вычисляется через силу трения и коэффициент трения.

На третьем этапе проводились расчёты, учитывающие нестационарные процессы по времени при вынужденных колебаниях. Расчёт переходных динамических процессов (Transient Analysis) является методом, используемым для определения динамического поведения системы при действии любых зависящих от времени нагрузок. В данном расчёте анализировалось поведение демпфера, и проводился анализ контактного взаимодействия поверхностей трения между демпфером и лопаткой. Для этого была разработана следующая методика: проводился расчет вынужденных колебаний при известном законе движения одного тела - лопатки, и рассчитывался отклик демпфера на воздействие со стороны колеблющейся лопатки. Причём, расчёт вынужденных колебаний учитывал изменение формы колебаний от прижатия демпфера. Такой подход обладает следующими преимуществами:

• -    для решения задачи нет необходимости построения всей модели лопатки с демпфером целиком, т.е. в расчётной модели присутствуют только части лопатки имеющие поверхности соприкосновения с демпфером, а демпфер присутствует целиком. Данное упрощение модели позволяет существенно сократить размерность задачи и в относительно короткое время провести расчёт;

• -    расчёты для оценки демпфирующей способности конструкции можно проводить по конкретным интересующим нас формам колебаний лопатки и соответствующей амплитуде напряжений или перемещений.

В расчётной модели задавались следующие граничные условия (рис. 6):

• -    гармонический закон колебания лопатки брался из расчета собственных форм и частот колебаний полноразмерной модели лопатки, когда учитывалось влияние демпфера. Закон прикладывался в виде перемещений на узлы. Уровень перемещений лопатки соответствовал уровню эквивалентных напряжений 10 кгс/мм² на входной кромке лопатки;

• -    гармонический закон проецировался на отдельную часть объёма лопатки: на контактирующую часть ножки лопатки;

• -    между демпфером и выделенными объёмами за-  - центробежная нагрузка учитывалась;

давался стандартный контакт с коэффициентом  - сила трения регулировалась центробежной на- трения k=0,2.                                     грузкой и натягом посадки демпфера.

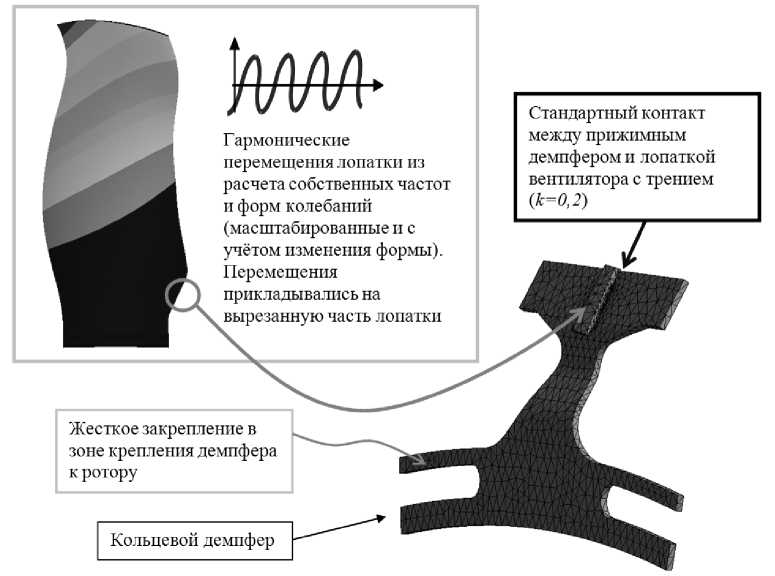
Кольцевой демпфер

Жесткое закрепление в зоне крепления демпфера к ротору

Г армонические перемещения лопатки из расчета собственных частот и форм колебаний (масштабированные и с учётом изменения формы). Перемещения прикладывались на вырезанную часть лопатки

Стандартный контакт между прижимным демпфером и лопаткой вентилятора с трением кк=0,2) "     "

Рис. 6. Конечно-элементная модель и граничные условия расчетной модели

По результатам расчёта определялся отклик демпфера, и высчитывалась совершённая работа силы трения на контактной поверхности между демпфером и лопаткой. На рис. 7 показан отклик демпфера на колебания лопатки, суммарная совершённая работа силы трения ∑ тр и изменение силы трения тр по времени. На рис. 8 изображены зависимости логарифмического декремента колебаний от величины силы трения по двум формам колебаний, в сравнении с результатами расчёта из расчёта собственных форм колебаний.

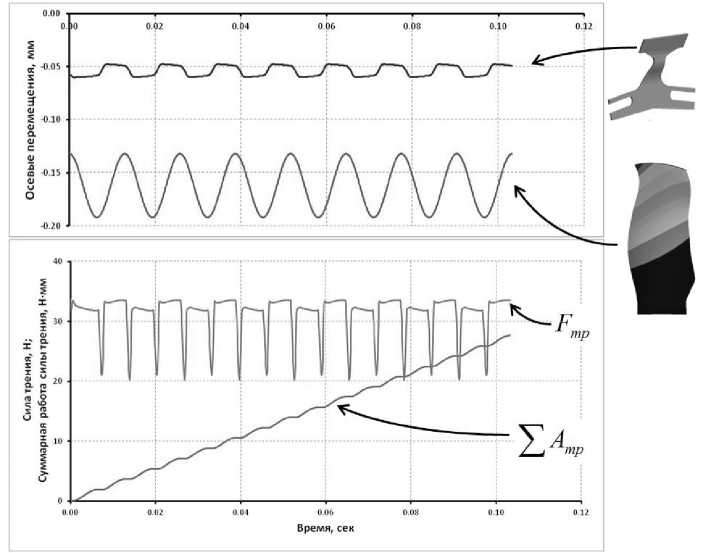
Рис. 7. Сверху – графики окружных перемещений демпфера и лопатки. Снизу – график суммарной совершённой работы силы трения и силы трения

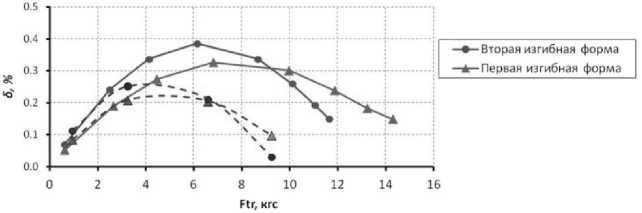
Рис. 8. Зависимость логарифмического декремента колебаний δ (%) от силы трения F _тр (кгс) по двум формам колебаний. Сплошные линии – расчёт собственных форм колебаний, штриховые линии – расчёт в нестационарной постановке

Анализ результатов показал следующее:

• -    в области при F_тр ≈0-3 кгс наблюдается качественная и количественная сходимость результатов расчёта в нестационарной постановке и в расчёте собственных форм колебаний по двум формам колебаний;

• -    при F_тр> 3 кгс наблюдается расхождение результатов расчётов. Расхождение объясняется следующим: наличием зон слипания (простаивания) демпфера с лопаткой, при расчёте собственных форм не учитывалась жесткость демпфера в окружном направлении.

Выводы:

• 1.    Расчётная экспресс-оценка эффективности демпфера даёт качественный результат, экономя вычислительный ресурс и машинное время. Кроме того полученную зависимость 8 ( F_тр ), можно масштабировать к результатам расчёта в нестационарной постановке.

• 2.    Расчёт в нестационарной постановке с учётом изменения формы колебаний позволяет выявить

тонкости математической модели, например, такие, как поведение демпфера. Расчёт без учета изменения формы колебаний даёт завышенное значение демпфирования в модели.

Для проверки эффективности прижимного демпфера для лопатки вентилятора запланированы экспериментальные исследования,     результаты экспериментального исследования будут использованы для уточнения расчётной модели или методики.