Расчётная оценка термодеформаций трёхслойной полупроводниковой структуры

Ульяновское отделение Института радиотехники и электроники РАН

Приведена математическая модель термодеформационных полей, образующихся в трехслойных полупроводниковых структурах прямоугольной формы, при воздействии на внешний слой кристалла локально распределенной поверхностной тепловой нагрузки, которая возникает в результате неустойчивости однородного распределения тока и приводит к пробою полупроводниковой структуры. Найден алгоритм численного решения, представлены результаты расчетов и их сравнение с результатами эксперимента.

Степень надёжности работы микросхем, а также другой микроэлектронной аппаратуры зависит от её защиты по отношению к различному сорту воздействий (механических, радиационных, магнитных и т.д.). Как было показано в работе [1], механические напряжения в полупроводниковых структурах вызваны рядом причин, таких как: механические деформации, которые возникают при изготовлении аппаратуры; различие коэффициентов линейного расширения материалов элементов, из которых со стоят изделия микроэлектроники; термонапряжения, появляющиеся в процессе функционирования микроэлектронной аппаратуры из-за неоднородности распределения температуры по объёму слоистой полупроводниковой структуры. Вообще говоря, последний вид напряжений появляется или вследствие неравномерного распределения температуры и её резкого локального роста (например, из-за неустойчивости тока по сечению эмиттера и стягивание его в шнур), или вследствие внешних связей, или при одновременном действии этих двух факторов. Так как влияние внешних связей хорошо известно [2], то ограничимся рассмотрением влияния неравномерного распределения температуры.

В работе [3] приведена расчётная математическая модель температурных полей, образующихся в трехслойных полупроводниковых структурах прямоугольной формы, при воздействии на внешний слой кристалла ло- кально распределенной поверхностной тепловой нагрузки, которая возникает в результате неустойчивости однородного распределения тока и приводит к пробою полупроводниковой структуры. Там же проводилась оценка температурных полей от J поверхностных источников тепла, которые можно задать в виде

J

q(x,y,t)=∑qj(x,y)Uj(t),       (1)

j = 1

где (индекс j опущен)

q(x, y) = ∫∫ q 0 (ξ, η)δ(x - ξ)δ(y - η)dξdη; (2)

(σ → 0)

∞

U=∑[u(t-nτ-t0)-u(t-τu -nτ-t0)]; (3)

n = 0

P0 (ξ, η) q0(ξ,η) =           ;

πr02

P₀ - тепловая мощность j-го источника; r₀ - радиус теплового пятна, получающегося от действия j-го источника; σ - площадь теплового пятна; u(t) - единичная функция Хевисайда; τ - период последовательности импульсов; τ_u - длительность импульса; t₀ - время начала действия j-го источника; n - число импульсов.

При оценке термодеформаций полупроводниковой структуры были сделаны следующие предположения:

• а)    распределение температур можно оп-

• ределять без учета деформаций тела, то есть в уравнениях теплопроводности отсутствуют члены, учитывающие взаимосвязанность механической и тепловой энергий;

• б)    деформации малы, так что можно пренебречь различием между координатами частицы до и после деформации, и что градиенты перемещения достаточно малы, поэтому можно пренебречь их произведениями;

• в)    материал везде ведет себя как упругий, то есть изменения температуры и напряжений не очень велики;

• г)    гипотеза Кирхгофа - Лява относительно того, что деформированная нормаль к рассматриваемой поверхности остается прямолинейной и несжимаемой.

В этих предположениях основные уравнения термоупругости пластин будут выглядеть следующим образом

D V 4 w =¹— V²M_Ts, (4) s Ts

• ^{(1 — V} s )

E t3

где D =---—--жесткость пластины на s 12(1-v2)

изгиб, отнесенная на единицу длины;

t _s /2

M Ts = ^a s E s J ^T(z)zdz ; E s - модуль Юнга; v s — - s / 2

• - коэффициент Пуассона; t_s = l_3s -l_3(s-1) - толщина пластины; a s коэффициент линейного температурного расширения; s = 1, 2, 3 - номер слоя.

Можно ввести приведенные коэффициенты [4]

Г             ^

_v _ у E k t k ^v k   у E k t k

v = L L

k = 1 (1 —V k ) [ k = 1 (1 — V k ) ,

E = (1 — V²)t ^{— 1} L —Ц-; t = L t k . (5) k = 1 ^{(1 —v} k )        k = 1

Были наложены следующие граничные условия: свободные боковые края всех пластин и внешняя верхняя поверхность первой пластины, остальные края принимались за-щемленными.Тогда можно записать по X:

d 2w   d 2w  MT

^D dx — ^v V ⁺ 1 T V

= 0;

d 3w d 3w 1  dMT

+ (1 — v)+T = 0: dx3         dxdy     (1 — v) dx dw

2)— = 0; dx по Y: (6)

_ d2w d2wMy

D—у — v—y + —-dy2     dx2

= 0;

d 3w d 3w 1

+ (1 — v)+T = 0: dy3         dydx2    (1 — v)

dw

• 2) у=0.

Начальное условие:

w(x,y,z,0) = 0.(7)

Так как нахождение аналитического решения задачи (4)-(7) представляет определённые трудности, то она решалась численными методами, причем конечно-разно стные уравнения составлялись аналогично рассмотренной выше в работе [3] задачи распределе-

Таблица. Механические характеристики среды

Слой	E, ГПа	v	а-10 "6, 1/К	Толщина, м
Кристалл ‒ Si	140	0,25	3	0,45-10-3
Припой ‒ (Pb + Sn)	48	0,33	25	0,05-10-3
Кристаллодержатель - Cu	120	0,38	17	1,5-10 -3

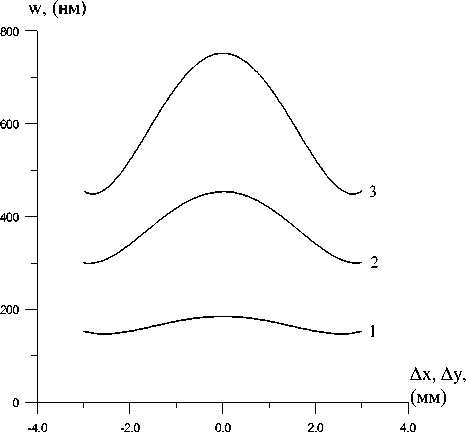
Рис.1. Распределение поперечных перемещений поверхности кристалла: P=30Вт; 1 ě 50 мс, 2 ě300 мс, 3 ě 500 мс ния температур. Была разработана программа совместного расчёта температурных и термодеформационных полей. Механические характеристики трёхслойной полупроводниковой среды (аналог мощного транзистора) приведены в таблице. Геометрические размеры в плоскости (XY) были равны l1= l2= 6⋅10-3 м, число точек по этим осям равно 10, а по оси Z равнялось 45.

На рис.1 показано распределение по-

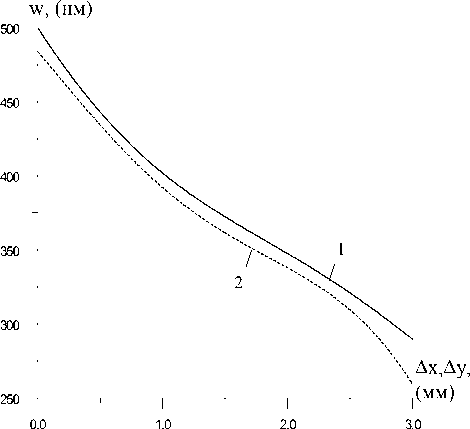
Рис.2. Зависимость поперечных перемещений поверхности кристалла от приближения механических характеристик слоёв:

1 ě таблица 1, 2 ě формула (5)

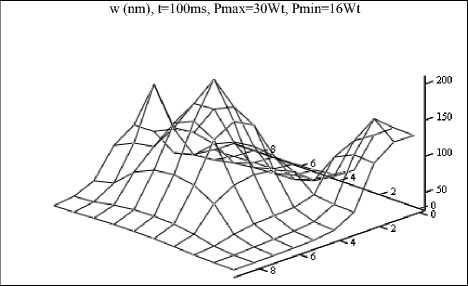
Рис.3. Профиль поверхности кристалла при действии трёх локальных источников тепла перечных перемещений w в нанометрах поверхности кристалла (z = 0) в зависимости от времени при действии источника тепловой мощности P=30 Вт, длительность разогревающего импульс а 500мс. Результаты расчета удовлетворительно согласуются с экспериментом [5].

Было проведено сравнение расчётных значений w при использовании усреднённых механических характеристик по формуле (5). Результаты сравнения приведены на рис.2, на котором кривая 1 соответствует кривой 2 рис.1. Видно, что различие составляет в среднем порядка 5%.

На рис.3 представлен профиль поверхности кристалла при действии трёх локальных импульсных источников тепла за время 100 мс, мощности источников одного 30 Вт, двух других по 16 Вт.

Работа выполнена в рамках проекта ФЦП "Интеграция".