Расчётно-экспериментальная идентификация активационных параметров модели изнашивания поверхностей трения

твёрдых тел рассматривает три типа (области) разрыва связей при совместном температурном и силовом ангармонизме колебаний атомов: в вершинах микротрещин; в ослабленных местах структуры; нормально нагруженных связей. В поверхностях трения конструкционных материалов ведущая роль принадлежит разрыву связей в вершинах микротрещин, что связано с наличием в материале технологических трещин, а также флуктуационным накоплением высокой плотности дефектов в локальных микрообъёмах и генерации из этих дефектов микротрещин (трещин). Область разрыва межатомных связей, в вершине микротрещины (трещины) представляет собой область локальной перегрузки в виде нано-микро-объёма V₀, перемещающегося по образцу по мере распространению фронта трещины. Высокая вероятность разрыва связей в локальном объёме V₀, по сравнению с другими микрообъёмами образца (см. объединённую модель повреждаемости и разрушения [3]), обусловлена не средним напряжением σ в сечении образца, а локальным напряжением в вершине трещины ∑= χσ , где χ – коэффициент локальной перегрузки в месте разрыва.

В основу предложенных моделей положена фундаментальная закономерность [1], связывающая напряжение, абсолютную температуру и долговечность t = τ0exp[(U0 - γσ)/kT], (1) откуда разрывное напряжение

σ _р= (1/ γ ) (U₀- kT ln(t/ τ ₀)), (2) где t – время до разрушения (долговечность) образца под нагрузкой, с; τ ₀= (10^-12…10^-13), с – период колебаний атомов в твердом теле; U₀ – энергия межатомной связи, Дж; Т – термодинамическая температура, ^oK; k=1,38 ^. 10^-23 Дж/^oK – постоянная Больцмана; γ – параметр (подгоночный), имеющий размерность объема, м³; энергия активации разрушения Δ U=(U₀- γσ ).

Теоретико-экспериментальным путем установлены значения активационных параметров [1]:

Y = (C/aE) x;

^p.max = Wy =Uo aEZ(Gx), при Т= 0°K; (3) X^p ^71   EE,, x EE*/^p ; U0 £*C/CT, где С – атомная (молярная) теплоемкость, Дж/oK (для одноатомных кристаллов С ~ 3k); a - коэффициент термического линейного расширения, oK–1; Е – модуль Юнга, Н/м2; σp – разрывное напряжение, Н/м2; σp.max – максимальное разрывное напряжение при Т = 0; ε* = 0,1…0,2 – относительное удлинение, при котором межатомная связь теряет устойчивость и разрывается; χ = ^/a = o^/Op = Es^/cTp - коэффициент локальной перегрузки в месте разрыва, созданный концентратором напряжения (Σ и σ – соответственно, локальное и среднее напряжения, σn= Eε*– предельная (теоретическая σth ) прочность).

Установленное совпадение величины U₀ с энергией сублимации Q (энергией межатомной связи), τ ₀ – c периодом колебаний атомов в твердом теле, а параметра γ , как меры локальной перезагрузки χ (3), с коэффициентом пропорциональности между ними С/ α E , позволили «интерпретировать механизм разрушения твердых тел с кинетической позиции как термофлуктуационный процесс распада межатомных связей и генерации зародышевых микротрещин» [1]. Освобождающаяся при разрыве связей энергия приводит к повышению плотности фононов hv = kT определенных частот v = Ту^т, Гц, где h= 6,626*10^-34 Дж/Гц – постоянная Планка, и влияет как на развитие образовавшегося дефекта, так и на возникновение и развитие соседних. С ростом плотности дефектов усиливается их взаимодействие, генерирование и распространение [5]. Накопление в приповерхностной зоне и на поверхностях трения единичных дефектов, образовавшихся в результате разрывов отдельных межатомных связей, приводит к кумулятивному образованию многочисленных локальных объемов материала V_oi с ослабленными связями. В этих объемах при разрывных напряжениях σ _pi , достигших усредненного предела прочности σ _B группы образовавшихся структурных элементов, происходит флуктуация и разрушение локального объёма образца на части, размеры которых определяются размерами элементов структуры или областей неоднородностей. В этой связи параметр γ в уравнении долговечности (1) приобретает совершенно иной физический смысл, а именно, смысл локального активационного объема

Y = ^ X = V_o,             (4)

в котором зарождается очаг разрушения и ожидается термическая флуктуация [5, 6], а время ожидания флуктуации t = Toexp[(Uo - k0o)/kT],       (5)

где V₀ – локальный активационный объем, м³;

– атомарный (молекулярный) объем, где α0– межатомное расстояние, αm – удлинение межатомной связи в момент разрыва.

При отсутствии дефектов χ =1, γ = V _A , а атермическая компонента прочности равна (3) предельной σ _n (теоретической) прочности. При наличии дефектов – χ > 1, γ = V ₀ = V _A χ , неоднородность (разрыв связей) в вершине микротрещины представляет собой область локальной перегрузки в виде микрообъема V ₀ , перемещающегося, как указывалось выше, по образцу по мере перемещения фронта трещины [1, 5]. Рассеяние значений параметра χ , например, для титанового сплава ВТ9, находится в пределах

χ = σ _n/ σ _p= ε _*E/ σ _в=0,1*1,1*10¹¹/(1,13*10⁹)≈10.

Математическое ожидание МО( χ )=10/2=5. Аналогичные пределы рассеяния коэффициента локальной перегрузки в месте разрыва для конструкционных материалов наблюдали авторы работы [2].

В связи с большим рассеянием значений параметра χi , (в пределах одного порядка), и, следовательно, уровней разрывных напряжений σpi на каждом дефекте и локальных объемов V0i , неравномерно распределенных в деформируемом объеме материала, разрушение их происходит как на поверхностях трения с отделением частиц износа, так и в глубинных слоях приповерхностной зоны без отделения частиц разрушения, так как активационные объемы блокированы матрицей исходного материала.

Математическая зависимость (5) активационного объема V0, энергии активации ΔU и времени ожидания флуктуации t позволила напрямую использовать эти параметры в расчетах скорости изнашивания при трении, положив, что каждая флуктуация, приводящая к разрушению локального объема V0, в каком бы месте деформируемого объема материала поверхностного слоя она ни произошла, в конечном итоге экви- валентна отделению с поверхности трения слоя материала толщиной bh = V0/Aa,             (6)

где Aa – номинальная площадь поверхности трения, м2; Δh – толщина отделяемого слоя матери- ала, м [3, 4]. Скорость износа

,

где V _h – скорость линейного износа, м/с; λ – число фрикционных связей (опорных точек) на поверхностях трения. Рассматривая совместно (7), (1), (2), (3) и приняв Ту¹ = V = kT/h, , Гц, получили обобщенную расчетную модель скорости изнашивания поверхностей трения в виде [4]:

kT Л h ovAa              Oy или с учетом выражения (3) для U0

£*C / 1 _ ^экв \

E.CkT Л         a \ tTp / y'-=V1T^exp--kT---

где σ заменено на

– эквивалентное напряжение на поверхностях трения, Н/м²; τ – касательное напряжение при трении; q _r – фактическое давление на контакте; µ – коэффициент трения; V – скорость скольжения; ρ – плотность; G – модуль сдвига. При вибротрении V=2π A ƒ, где A – амплитуда, мм; ƒ – частота осцилляции, Гц.

Анализ уравнений (8) и (9) показывает, что при            преимущественна роль термо флуктуационного разрушения.

При значениях            энергия активации ΔU= U=               (5), работа внешней силы становится больше или равной энергии связи атомов в твердом теле , а экспоненциальный член в уравнении (8) exp(-0)=1, что приводит поверхностный слой в состояние низшей прочности и к ведущей роли атермического механизма разрушения. Тогда уравнение (8) перепишется в виде yr __ £*C kT <7ЭКВ Л .

Сложная взаимосвязь физических, механических и геометрических параметров, входящих в уравнения (9,10) скорости изнашивания, определила выбор аналитико-экспериментального метода идентификации расчетной модели. Экспериментальная проверка проведена с использованием результатов стендовых испытаний на износ при фреттинге без смазки лабораторных образцов из сплава ВТ9. Критерием идентификации принята степень соответствия расчетных значений скорости изнашивания экспериментальным. Экспериментальные значения определяли на всех режимах испытаний (рис.1) путём линейной аппроксимации экспериментальных кривых на стадии установившегося износа. Расчётные значения определяли по уравнению (10) при варьировании параметров внешних механических воздействий и при следующих постоянных исходных данных: q_дин = 3 МПа; Т = 293^оК; A _a = 30 ^. 10^-6 м²; σ _В =1130 ^. 10^-6 H/м²; Χ =1030 ^. 10^-6 H/ м²; G = 0,38 E; E = 1,1 ^. 10¹¹ H/м²; ρ = 4480 кг/ м³; ε = 0,1; C = 3k; k = 1,38 ^. 10^-23Дж/^оК; α = 8,5 ^. 10^-6 K^-1; h = 6,626 ^. 10^-34 Дж/Гц.

Фактическую площадь и сближение в контакте, необходимые для расчёта среднего фактического давления, определяли для случая контакта двух шероховатых поверхностей с одинаковыми параметрами микрогеометрии. Для этого вычисляли эквивалентные (приведённые) характеристики микрогеометрии по формулам, полученным [8] при свёртке двух опорных кривых профилей.

Из приведённых (рис. 1) данных следует, что предложенное расчётное уравнение качественно и количественно правильно описывает процесс изнашивания и его функциональную связь с

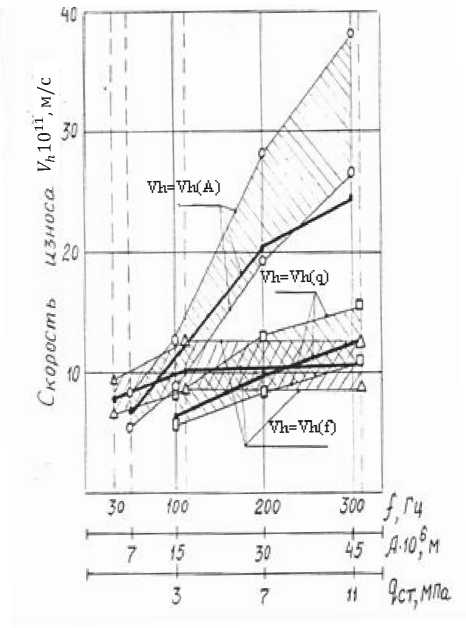
Рис. 1. Зависимость скорости линейного износа сплава ВТ9 от амплитуды ( ƒ=310 Гц, q_ст=7 МПа), давления (А = 0,015 мм, ƒ = 110 Гц) и частоты (А = 0,015 мм, q_ст=7 МПа).

qдин= 3 МПа, Т = 293оК. Заштрихованы области расчётных значений скорости износа.

Жирные линии – экспериментальные значения.

физическими и механическими свойствами материала. Экспериментальные значения скорости изнашивания попадают в область расчётных значений, обусловленную рассеянием механических ( σ _В , σ _T при коэффициенте вариации W = 0,177) и физических (С, α ) свойств материала. Коэффициент вариации средних значений V_hр и V_hэ не превышает 0,215.

Скорость линейного износа сплава в установившемся режиме фреттинга слабо возрастает с увеличением частоты (скорости) осцилляции, более интенсивно с ростом нормального давления, что связано, очевидно, с ростом эквивалентного напряжения. Увеличение амплитуды осцилляции приводит к росту скорости относительного проскальзывания, перекрытия на пятнах фактического контакта и активационного объёма материала, к смене характера контактного взаимодействия и изнашивания, что в совокупности, очевидно, ведёт к резкому повышению скорости линейного износа (рис. 1). При проскальзывании превышающем диаметр пятна контакта d (А≥20 мкм, рис. 1), характер контактирования, очевидно, меняется, что согласуется с установленными амплитудными границами протекания фреттинг – износа.

В табл. 1 приведены расчётные и полученные нами экспериментальные значения скорости изнашивания сплава ВТ9 в разных температурных режимах испытаний. В табл. 2 приведено сравнение расчётных данных с результатами высокотемпературной фреттинг-корозии титановых сплавов ВТ8, ВТ3-1, ОТ4 и стали 20Х13, полученных авторами работы [9]. В том и в другом случаях исходили из условий реализации пластического контакта микронеровностей, полагая при малых номинальных давлениях qr=1,1σT (табл. 1), а при больших – qr=3σT (табл. 2). При определении экспериментальных значений скорости изнашивания использовали величину суммарной повреждаемости U+H для каждого температурного режима, где U – износ, H – глубина повреждений от схватывания.

Таблица 1. Расчётные и экспериментальные значения скорости изнашивания сплава ВТ9 при варьировании температуры: A= 15 ^. 10^-6 м; f= 310 Гц; q_ст= 7 Мпа; q_дин= 3 МПа; N= 300 Н; d≈ 2 А; q_r= 1,1 σ _T

Температура Т, К0	Коэф-фици-ент трения, р	Механические свойства сплава		Скорость изнашивания V h *10L1 м/с
		^в * I0-6, H/м2	от * I0-6, H/м2	Расчетная, V hp	Экспериментальная, V hэ	Коэффициент вариации, W	Экспериментальная по данным	Коэффициент вариации, W
293	0,54	1130	1030	10,5	11,62	0,107	12,41	0,18
273	0,47	1070	960	16,41	18,51	0,13	13,25	0,19
473	0,44	995	875	20,54	21,29	0,04	25,25	0,23
573	0,53	920	790	31,65	32,87	0,03	30,51	0,04
600	0,55	900	770	35,03	34,41	0,02	34,93	0,003
673	0,63	834	706	48,22	46,29	0,04	42,71	0,114

Таблица 2. Расчетные и экспериментальные значения скорости изнашивания при высокотемпературной фреттинг-коррозии материалов [9]:

A= 100 ^. 10^-6 м; f= 30 Гц; q_ст= 19,6 Мпа; А_а= 50 ^. 10^-6 м²; N_ц= 5 ^. 10⁵ циклов; d= 30 ^. 10^-6 м; q_r= 3 σ _T

Материал	Температура Т, Ко	Суммарное повреждение (U+H) * 106, м	Коэффициент трения, р	Свойства материала	Скорость изнашивания V h *1011, м/с
					расчетная	Экспериментальная	Коэффициент вариации
ВТ8	453	36	0,44	ав =940*10 6 Н/ м2; ст =800*10 6 Н/ м2; Е=1,1*10п Н/ м2; а=8,5*10-6 К-1; р=4480 кг/м3	219,74	216	0,017
ВТ3-1	468	32	0,44	ов =883*10 6 Н/ м2; ат =716*10 6 Н/ м2; Е=1,1*10и Н/ м2; а=9,3*10-6 К-1; р=4500 кг/м3	210,4	192	0,087
ОТ4	483	40	0,44	ав =610*10 6 Н/ м2; ат =540*10 6 Н/ м2; Е=1,1*10и Н/ м2; а=8,5*10-6 К-1; р=4500 кг/м3	375,6	240	0,36
20X13	458	46	0,5	ав =590*106 Н/ м2; ат =460*10 6 Н/ м2; Е=2,1*10и Н/ м2; а=10,5*10-6 К-1; р=7850 кг/м3	298,34	276	0,075

Сопоставление данных табл. 1 и табл. 2 показывает, что расчет удовлетворительно согласуется с экспериментом. В большинстве случаев рассеяние экспериментально зарегистрированных скоростей износа вокруг расчётных значений не превышает ±23% (табл. 1).

Значения могут варьировать в диапазоне не более ±36% (табл. 2). Такие расхождения, учитывая вероятностный характер температурных значений механических свойств материалов и стохастический характер изнашивания в широком температурном интервале, можно считать приемлемыми. Уравнение (10) адекватно описывает изнашивание как лабораторных образцов из титановых сплавов и других материалов (табл. 1; 2), так и натурных деталей машин при стендовых испытаниях на фреттинг-коррозию и в условиях эксплуатации. К числу последних можно отнести детали лопаточных аппаратов [10] газотурбинных двигателей.

Как показали длительные стендовые испытания двигателей [10], при наработке порядка 1500 ч. происходила частичная потеря предварительного натяга на бандажных полках лопаток, собранных в колесо то есть на некоторых участках по окружности колеса между контактными площадками полок появлялся зазор. С увеличением времени наработки таких участков становилось больше и при наработке более 3000…4000 ч. натяг исчезал полностью. Учитывая неравномерность износа, распределения контактной нагрузки на площадках полок, а также различный характер их контактирования (от пластического до упругого) по окружности колеса, расчётные значения износа определяли в предположении пластического контактного взаимодействия неровностей (q_r= 1,1 σ _T ) и переходного от пластического к упругому (q_r≈3 σ _T ), при относительном проскальзывании полок в пределах элементарного пятна контакта 2А≈d.

Износ при стендовых испытаниях двигателей (табл. 3), в некоторых случаях превышает расчётные значения. Это связано, очевидно, с тем, что при определении экспериментальных значений износа использовались не средние, а максималь- ные значения зазора δ [10] между контактными площадками полок (U=δ/2, где δ – наибольший зазор).

Результаты идентификации показывают, что предлагаемая расчётная модель изнашивания в целом не противоречит имеющимся экспериментальные данным.

Размерная идентификация активационных параметров модели изнашивания сплава ВТ9:

χ = σ _n/ σ _в= ε _*E/ σ _в=(0,1 . 1,1 . 10¹¹)/(1130 . 10⁶)=10;

MO_{( χ )} =10/2=5;

U₀= ε _*C/ α =(0,1 ^. 3 ^. 1,38 ^. 10^-23)/(8,5 ^. 10^-6)= =0,0487 ^. 10^-17Дж;

V_A=C/( α ^. E)=(3 ^. 1,38 ^. 10^-23)/(8,5 ^. 10^{-6 . .} 1,1 ^. 10¹¹)=4,4278 ^. 10^-29 м³ ;

V 0min = V A =4,4278 . 10^-29;

V 0max = V A χ =4,4278 . 10^-28 м³

Представленные параметры размерной идентификации модели изнашивания поверхности трения адекватны параметрам, приведённым в работах [1, 2, 5, 6].

В заключение следует отметить, что стимуляторами применения предложенных моделей изнашивания при трении могут стать: прямое использование физических и механических параметров и констант материалов; полное отсутствие эмпирических (подгоночных) коэффициентов; применение не «назначенных» для разрушения деформируемых объемов материала с неопределенными размерами и границами, например объём материала взаимно внедрившихся микронеровностей контактирующих поверхностей или объём материала внедрившихся субмикронеровностей на границах зёрен, а локальных активационных объемов, формируемых в процессе деформации по естественным термофлуктуационным механизмам; использование фундаментальной прямой связи образовавшихся активационных объемов с временем ожидания их флуктуаций (разрушения). В основу разработки физической модели накопления повреждений и разрушения положена широкая идентификация ее параметров методами механических испытаний на трение и износ, рентгеноструктурных,

Таблица 3. Расчётные и эксплуатационные значения износа бандажных полок рабочих лопаток из сплава ЖС6КП первой ступени турбины ГТД [10]:

Т= 1173 ^оК; σ _в = 765 ^. 10⁶ Н/ м²; σ _T=510 ^. 10⁶ Н/ м²; Е=2,1 ^. 10¹¹ Н/ м²; ρ =8100 кг/м³; α =17 ^. 10^-6 К^-1;

μ₀= 0,3; А_а= 120 ^. 10^-6 м²; A= 15 ^. 10^-6 м; f= 310 Гц; μ= 0,4; d=2А= 30 ^. 10^-6 м;

Время наработки t, ч Расчетные значения износа U, мм Износ при стендовых испытаниях U=8/2, мм Контакт упруго -пластический Контакт пластический U1 U2 U3 1000 0,168 0,205 - 0,0625 - 2000 0,337 0,412 0,375 - 0,5 3000 0, 505 0,616 0,75 1,05 1,125 4000 0,67 0,821 - - - 5000 0,84 1,026 0,9 1,1 1,3 электроннооптических, электронографических и аналитических исследований, подтвердивших ее адекватность.