Расчётно-экспериментальные исследования динамических характеристик макета рамы телескопа космического аппарата
Автор: Иголкин А.А., Сафин А.И., Кузнецов А.В.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 4 т.25, 2024 года.
Бесплатный доступ
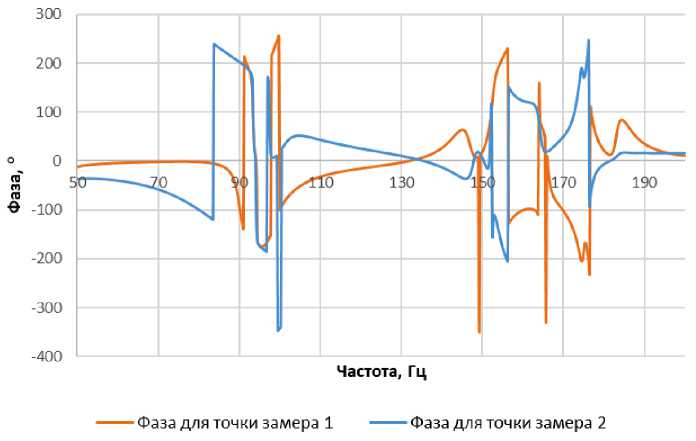
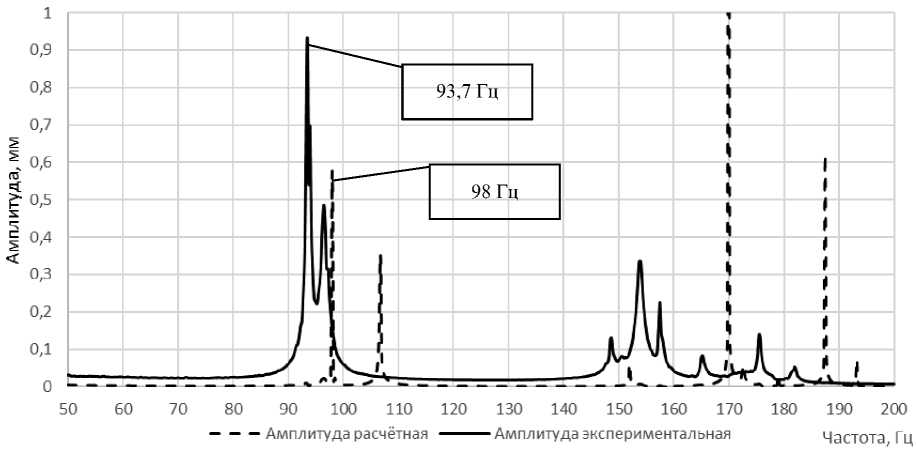
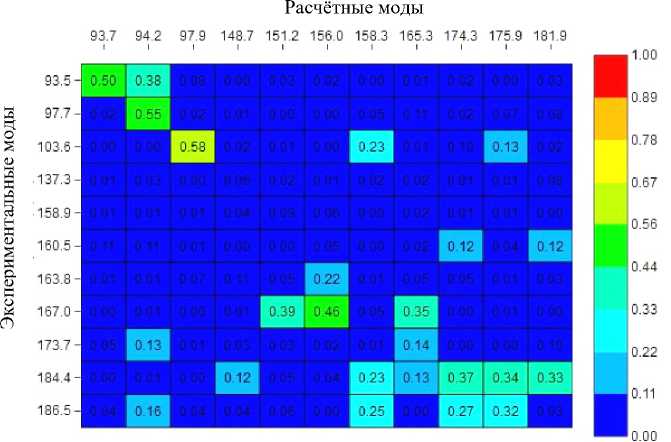
В статье представлено расчётно-экспериментальное исследование динамических характеристик макета рамы телескопа космического аппарата. Основное внимание уделено методике проведения вибродинамических испытаний с использованием трёхкомпонентного лазерного виброметра и созданию конечно-элементной модели исследуемого макета. Для анализа динамики конструкции определены основные критерии, такие как модальные параметры, валидация модели и гармонический анализ. Особое внимание уделяется влиянию преобразования экспериментальных данных на точность расчёта критерия модальной достоверности. Исследован макет рамы телескопа, представляющий собой ферменную конструкцию, закреплённую на пружинах. Испытания проводились путём приложения случайного воздействия типа «белый шум». Получены динамические характеристики конструкции, включая собственную частоту колебаний, которая составила 93,7 Гц. Экспериментальные данные сравнивались с результатами конечно-элементного моделирования, показавшими значительное расхождение между ними, особенно в области собственных частот. Это свидетельствует о необходимости корректировки конечно-элементной модели. Рассмотрены различные критерии оценки соответствия расчётных и экспериментальных моделей, такие как координатный критерий модальной достоверности (COMAC), критерий модальной достоверности (MAC), взаимный критерий гарантии (CSAC) и взаимный коэффициент пропорциональности (CSF). Эти критерии помогают оценить степень совпадения форм колебаний и частотных характеристик. Проведён анализ влияния преобразований экспериментальных данных в разные единицы измерения на результаты расчётов этих критериев. Сделан вывод о том, что текущая расчётная модель требует доработки и уточнения параметров для достижения лучшего соответствия с реальностью.
Модальные параметры, конечно-элементная модель, валидация, гармонический анализ, критерии модельной достоверности, амплитудно частотные характеристики
Короткий адрес: https://sciup.org/148330570
IDR: 148330570 | УДК: 534.12 | DOI: 10.31772/2712-8970-2024-25-4-423-432
Текст научной статьи Расчётно-экспериментальные исследования динамических характеристик макета рамы телескопа космического аппарата
В сложившейся тенденции отработки на вибрационную прочность конструкций космического аппарата (КА) с применением в качестве объекта исследования его первого лётного образца, а соответственно с применением расчётно-экспериментальных методик, задача коррекции конечно-элементной модели (КЭМ) по результатам экспериментальной отработки всё больше набирает актуальность [1–8]. В то же время, большое распространение получают бесконтактные методы получения динамических характеристик, несомненным плюсом которых является возможность проведения испытаний очень небольших и лёгких конструкций [9; 10]. Коррекция КЭМ по результатам испытаний может осуществляться прямым или итерационным методом. Также методы коррекции КЭМ можно классифицировать по использованию частотных и модальных характеристик объекта исследования [11; 12]. Как известно, использование частотных характеристик (FRF) имеет преимущества перед использованием модальных данных, так как последние обычно извлекаются из ограниченного количества точек вокруг резонирующих пиков на кривых FRF со свойственными числовыми ошибками, в то время как FRF содержит информацию от полного спектра частот. Каждый из методов характеризуются расчётом своих критериев. Однако использование различных критериев, таких как координатный критерий модальной достоверности (COMAC) с критерием модальной достоверности (MAC) [уравнение (1)] – для модальных данных и критериев для частотных данных – взаимный критерий гарантии (CSAC) [уравнение (2)] и взаимный коэффициент пропорциональности (CSF) [уравнение (3)], сводится к получению числового значения или таблице значений, которые располагаются в диапазоне от 0 до 1. В статье представлен пример расчёта некоторых из указанных критериев с учётом особенностей обработки экспериментальных данных и влияние погрешностей сопоставления расчётной и экспериментальной сеток.
Анализ корреляции функции частотных характеристик между парами в каждой точке частоты оценивается с точки зрения взаимного критерия адекватности (CSAC) и взаимного коэффициента пропорциональности (CSF). CSAC является мерой корреляции формы между экспериментальными и аналитическими частотными характеристиками в пределах от 0 до 1 [уравнение (2)]. Между тем CSF является мерой различия в амплитуде между измеренными и рассчитанными откликами в пределах от 0 до 1 [уравнение (3)]. В целом, эти две корреляционных функции ФЧХ могут быть известны как функции взаимной корреляции подписи (CSC). Обычно они выражаются в единице процента (%) для лучшей интерпретации.
|
Номера узлов расчётных |
Номера узлов экспериментальных |
COMAC_X |
COMAC_Y |
COMAC_Z |
|
290 |
40 |
0,1958 |
0,0720 |
0,2889 |
|
1971 |
44 |
0,1307 |
0,1043 |
0,0776 |
|
2014 |
46 |
0,1958 |
0,1039 |
0,2852 |
|
2262 |
34 |
0,0745 |
0,1285 |
0,0510 |
|
2636 |
48 |
0,0783 |
0,1071 |
0,0388 |
|
2810 |
41 |
0,0739 |
0,1701 |
0,0414 |
|
1112009 |
50 |
0,3968 |
0,1229 |
0,2258 |
|
1112068 |
35 |
0,1067 |
0,1174 |
0,0801 |
|
1112141 |
47 |
0,2412 |
0,0529 |
0,0783 |
|
1112211 |
26 |
0,1467 |
0,1729 |
0,1058 |
|
1112271 |
39 |
0,1165 |
0,0495 |
0,1674 |
|
1112280 |
23 |
0,1283 |
0,0812 |
0,1367 |
Полученные значения указанного критерия, а также среднеарифметическое значение представлены на рис. 5.
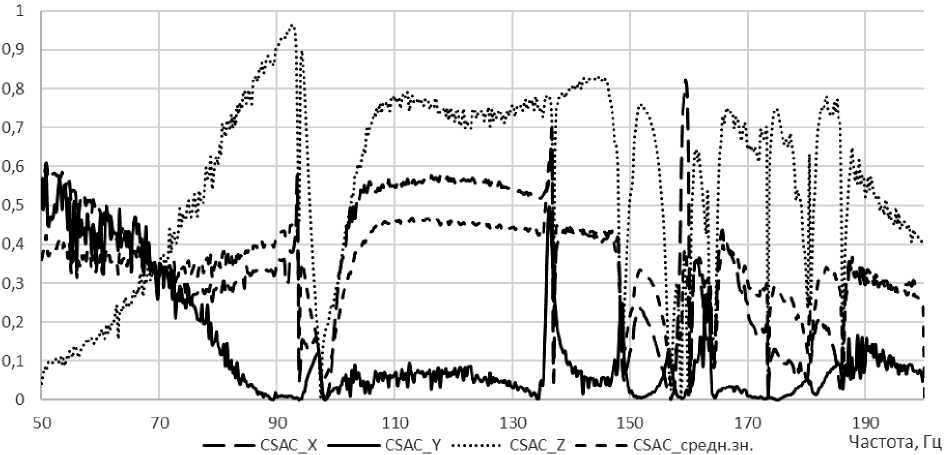
Рис. 5. Значения критерия CSAC по FRF виброперемещениям
-
Fig. 5. Values of the CSAC criterion for FRF vibration displacements
Анализ полученных данных показывает, что результаты расчётной модели не соответствуют динамике конструкции по оси Y в большей степени, чем по другим осям. В области собственных частот расчётная модель даёт полное расхождение с экспериментом, а в диапазоне частот от 100 до 145 Гц наиболее соответствует поведению нагруженной конструкции по осям Z и X.
Аналогично критерию CSAC, CSF так же учитывает ось и направление, что сказывается на характере кривой CSF. Однако данный критерий характеризует соответствие по амплитуде колебаний, что в свою очередь приводит к зависимости от приложенных усилий. Так как предшествующий расчёт CSAC показал несоответствие расчётной и экспериментальной модели, то расчёт критерия CSF не может иметь достоверных характер. На рис. 6 показана близость по характеру критериев CSAC и CSF для одной и той же оси (для примера взята ось Z), а также зависимость критерия CSF от значения приложенных усилий.
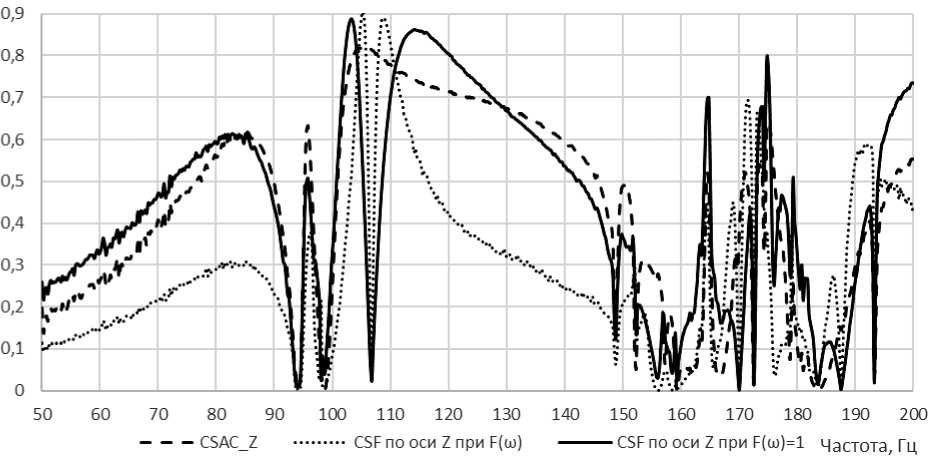
Рис. 6. Результаты расчёта критерия CSAC для оси Z; CSF при нагрузке в виде зависимости силы от частоты F(ω), соответствующей экспериментальным данным; CSF при нагрузке в виде единичной силы в рассматриваемом диапазоне частот
-
Fig. 6. Results of calculating the CSAC criterion for the Z axis; CSF under load in the form of a dependence of force on frequency F(ω), corresponding to experimental data; CSF under load in the form of a unit force in the frequency range under consideration
Для количественного сравнения результатов соотношения расчётных и экспериментальных данных приведём к среднему значению в процентном отношении критерии MAC по формуле
-
(4) и CSF по формуле (5):
MAC %
n
E MAC
i = 1
n
X 100 %,
к 7
где n – собственные частоты,
CSF %
( n^ У
E CSFi
-— n
X 100 %,
к 7
где n – дискретные частоты всего диапазона измерений.
Полученные значения МАС ср.зн. = 29,5 %; CSF ср.зн. = 34,8 % указывают на то, что корреляция экспериментальных и расчётных форм по резонансным частотам в рассматриваемой системе ниже, чем корреляция экспериментальных и расчётных частотных характеристик во всём рассматриваемом диапазоне частот.
Проведённое исследование показало важность использования современных методов вибро-динамических испытаний и создания точных конечно-элементных моделей для анализа динамических характеристик конструкций космических аппаратов и их составных частей. Представленные методики позволяют получать детальную информацию о поведении макетов рам телескопов под воздействием внешних нагрузок, что критически важно для проектирования надёжных и долговечных космических аппаратов.
Были выявлены существенные расхождения между расчётными и экспериментальными данными, особенно в области собственных частот, что подчёркивает необходимость тщательной калибровки и корректировки конечно-элементной модели. Применение различных критериев оценки соответствия, таких как COMAC, MAC, CSAC и CSF, помогает выявить слабые стороны модели и определить пути её улучшения.
Дальнейшие работы должны быть направлены на выбор оптимальных варьируемых параметров и установление границ их значений для проведения эффективной процедуры коррекции модели. Только таким образом можно достичь высокой точности прогнозирования поведения реальных конструкций в условиях эксплуатации и обеспечить надежность и безопасность космических миссий.
Описанные в настоящей работе научно-исследовательские результаты получены в рамках выполнения и за счёт средств гранта РНФ 23-19-20025.
The research results described in this work were obtained within the framework of and at the expense of the RSF grant 23-19-20025.
Список литературы Расчётно-экспериментальные исследования динамических характеристик макета рамы телескопа космического аппарата
- Об оценке расходования механического ресурса конструкции российского сегмента Международной космической станции / А. В. Анисимов, Н. Ю. Введенский, А. И. Лиходед и др. // Космонавтика и ракетостроение. 2011. № 1(62). С. 74–79.
- Комаров, И. С. Наземная экспериментальная отработка изделий ракетно-космической техники на ударное воздействие от пиротехнических средств // Труды МАИ. 2013. № 71 [Электронный ресурс]. URL: https://trudymai.ru/upload/iblock/a18/a181f426004cc5762b6e7e87795eb545.pdf?lang=en&issue=71 (дата обращения: 05.09.2024).
- Хатунцева О. Н., Шувалова А. М. О дополнительных «многомасштабных» критериях подобия для экспериментальной отработки изделий аэрокосмической техники // Вестник Москов. авиац. ин-та. 2023. Т. 30, № 1. С. 91–97. DOI: 10.34759/vst-2023-1-91-97.
- Особенности наземной экспериментальной отработки крупногабаритных солнечных батарей / С. А. Захаров, В. И. Кузоро, Н. А. Тестоедов, В. И. Халиманович // Наукоёмкие технологии. 2016. Т. 17, № 7. С. 22–28.
- Введенский Н. Ю., Пустобаев М. В. Анализ отработки космической техники на механические воздействия в США, ЕС и РФ // Вопросы электромеханики. 2012. № 130. С. 19–26.
- Безмозгий, И. М., Софинский А. Н., Чернягин А. Г. Моделирование в задачах вибропрочности конструкций ракетно-космической техники // Космическая техника и технологии. 2014. № 3(6). С. 71–80.
- Межин В. С., Обухов В. В. Сравнительный анализ методов экспериментального подтверждения конечно-элементных моделей конструкции космических аппаратов // Космическая техника и технологии. 2016. № 4(15). С. 14–23.
- Balyakov D. F. Verification of finite-element model spacecraft via test results // Siberian Journal of Science and Technology. 2018. Vol. 19, No. 1. P. 8–16.
- Lieven N. A. J., Waters T. P. The application of high-density measurements to dynamic finite element reconciliation // Proceedings of IMAC 13. 1995. P. 185–192.
- Бесконтактная регистрация и анализ вибрации изделий машиностроения с помощью трёхкомпонентного лазерного виброметра / А. А. Иголкин, А. И. Сафин, Г. М. Макарьянц, Е. В. Шахматов // Прикладная физика. 2013. № 4. С. 49–53.
- Allemang R., Brown D. A correlation coefficient for modal vector analysis // 1st International Modal Analysis Conference. Orlando, USA, 1984.
- Dascotte E., Strobbe J. Updating Finite Element Models Using FRF Correlation Functions // Proceedings of the 17th IMAC Conference. Kissimmee, Florida, 1999. Р. 1169–1174.
- Heylen W., Lammens S., Sas P. Modal analysis theory and testing. М.: Novatest, 2010. 319 p.
- A poly-reference implementation of the least-squares complex frequency-domain estimator / P. Guillaume, P. Verboven, S. Vanlanduit at al. // Proceedings of IMAC 21, the International Modal Analysis Conference, Kissimmee (FL), USA, February 2003.
- Parametric Identification of Transfer Functions in the Frequency Domain – a Survey / R. Pintelon, Guillaume P., Rolain Y. at al. // IEEE Trans. Autom. Control. 1994. Vol. AC-39, No. 11. P. 2245–2260.