Расчётные и экспериментальные исследования обтекания высотных зданий и сооружений атмосферным ветром в условиях городской застройки

Специализированные АДТ должны обеспечить возможность реализации в них режима потока типа приземного ветрового слоя (ПВС) с определенным профилем средней скорости по высоте. При этом размеры рабочей части АДТ должен обеспечивать размер моделей, достаточный для реализации «автомодельного» режима обтекания, т.е. независимость аэродинамических характеристик от числа Рейнольдса: Re = ∞ , где V∞ — скорость по-ν тока, где D — характерный поперечный размер модели, ν — коэффициент кинематической вязкости.

Именно реализация автомодельного режима позволяет получать в модельном эксперименте натурные значения аэродинамических коэффициентов без пересчета «на натуру». Нижняя граница значения числа Re по опыту исследования обтекания плохообтекаемых объектов [2] составляет порядка 2 · 10 ⁵ . Это исключает возможность применения «комнатных» АДТ с характерным размером моделей в несколько сантиметров.

В настоящей работе показана основанная на интенсивных предварительных расчётах средствами вычислительной аэродинамики технология экспериментального определения аэродинамических характеристик высотных зданий и сооружений в условиях городской застройки (рельефа местности) [3].

В качестве объекта исследования рассмотрено проектируемое для строительства в Москве высотное здание (рис. 1).

Рис. 1. Проектируемое высотное здание

Математическое моделирование предоставляет возможность предварительного анализа характера и структуры обтекания здания ветровым потоком, а также рационального определения масштаба модели для АДТ, степени влияния окружающей застройки (городского ландшафта) на исследуемый объект и величины наиболее критичных углов направления ветра. Более подробное описание данной методики может быть найдено в работе [3].

В соответствии с методикой проведена серия расчётов в рамках краевой задачи для стационарных осредненных по Рейнольдсу уравнений Навье–Стокса с SST-моделью замыкания, описывающих течение вязкой несжимаемой жидкости. Набегающий поток имеет заданный профиль скорости приземного ветра. Для проведения расчетов построена блочная структурированная сетка с призматическим подслоем на поверхности земли, состоящим из 20 ячеек, имеющим высоту первой ячейки 0.01 м и коэффициент роста ячеек 1.2. Общий объем сетки составляет 5 млн ячеек, притом около половины приходится на призмати- ческий подслой. Технология проведения расчётных исследований изложена в [4], пример моделирования атмосферного течения над горным ландшафтом приведен в работе [5].

При решении задачи все переменные приведены к безразмерному виду. Расчет проводился до выхода величин интегральных осредненных нагрузок на стационарные значения. За характерные линейный размер и скорость приняты D =27м ,V _∞ = 20 м / с, так что Re = 2 · 10 ⁵ . При таких значениях течение автомодельно по числам Рейнольдса.

На рис. 2 приведён общий вид высотного комплекса и окружающей застройки, а на рис. 3 приведены пять направлений ветра, для которых проводился подробный сравнительный анализ.

В табл. 1 представлены сравнительные значения коэффициентов сопротивления C _x и боковой силы C _y для здания при наличии полной окружающей застройки и для здания с сокращёным вариантом застройки, когда сохраняется только ближайшее здание, C _{x упр} и C y упр ^.

Из сравнения видно, что отброшенная часть окружающей застройки не вносит существенного искажения в интегральные аэродинамические характеристики проектируемого высотного здания, в связи с чем в состав модели в масштабе 1:130 было включено ближайшее здание, изображённое на проектном эскизе (рис. 1). Максимальное загромождение рабочей части при этом составило 9,5%.

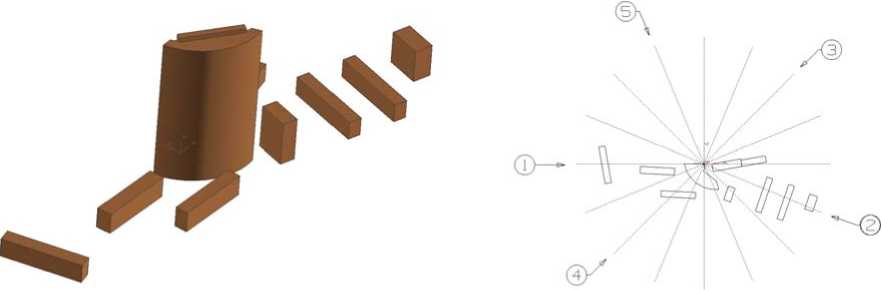
Рис. 2. Заложенная в расчёт геометрия высотно- Рис. 3. Направления ветра, при которых получе-го здания и окружающей застройки           ны эпюры

Таблица 1

Направление 1 2 3 4 5 Cx 0,50 0,24 1,14 1,01 0,45 Cy 0,28 0,69 0,10 0,08 –0,94 Cxупр 0,50 ,260 1,18 1,07 0,49 Cyупр 0,22 1,02 0,13 0,09 –0,77 кального градиентного профиля средней скорости. Последний образуется в рабочей части АДТ-2 при работе трубы в полной конфигурации Т1/Т2 в диффузорном течении между рабочими частями Т1 и Т2 с системой «макрошероховатостей» на длине 50–60 м. Типичные профили средней скорости и интенсивности турбулентности по высоте приведены на рис. 6.

Рис. 4. Заложенная в расчёт геометрия высотного здания и окружающей застройки

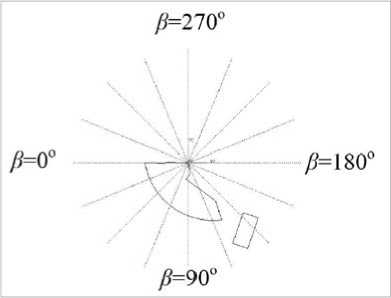
Рис. 5. Направления ветра, при которых получены эпюры

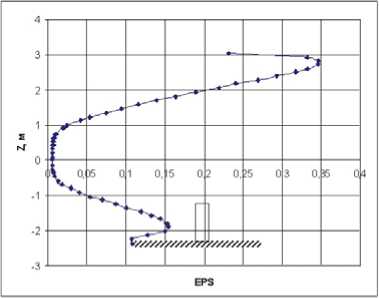
а)

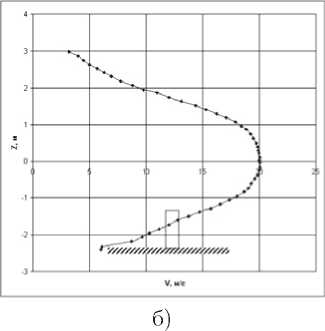
Рис. 6. Типичные профили средней скорости и интенсивности турбулентности по высоте

Сравнение интегральных характеристик

Средние аэродинамические нагрузки – лобовое сопротивление X , боковая сила Y и крутящий момент M _z – определялись на автоматических рычажно-рейтерных весах АВТ-1 со струнной подвеской модели. На подвеске крепилась «взвешиваемая» модель, не имеющая механической связи с моделью здания застройки, расположенной на круговом экране. При повороте модели на поворотном устройстве весов на очередной угол β на этот же угол поворачивался экран с моделью здания застройки, формирующей, таким образом, точное моделирование течения при любом угле ветра.

Аэродинамические коэффициенты соответствующих сил и момента определялись соот- ношениями

C x

X      Y      Mz qS = qS ’ mz = qSb

ρV _∞ ²

где V^ — скорость на верхней границе ПВС или на входе в рабочую часть АДТ, S = bH – характерная площадь модели; b – характерный поперечный размер (ширина по острым углам здания); H - высота модели. Для комплекса моделей масштаба 1:130: Н = 0,97 м, b = 0,62 м, S = 0,6 м2. Определение нагрузок на натурный объект осуществляется по полученным натурным значениям коэффициентов путем «обращения» вышеприведенных формул: X = CxqS, Y = CyqS, Mz = mxqS. Эпюра нагрузок в сечениях по высоте, например, X получается с использованием коэффициента и значения скорости на данной высоте h:

X ( h ) = C x S

P ( V ( H )) 2

На рис. 7 показана зависимость коэффициента лобового сопротивления C _x здания от скорости V _∞ для углов ветра β = 225° (верхняя кривая) и 315° (нижняя кривая). Начиная со скорости 10 м/с, величина остаётся неизменной, т.е. режим автомодельности имеет место при V _∞ > 10 м/с. На основании чего выбрана рабочая скорость потока V _∞ = 20 м/с.

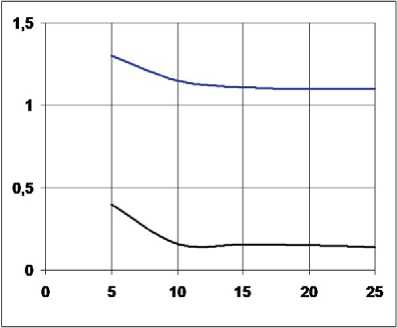
Рис. 7. Зависимость C x ( V ^ )

Модель здания оборудована на четырех уровнях, соответствующих натурным высотам 25, 55, 90, 125 м, датчиками давления для измерения средних и мгновенных значений давления, Измерение давления производилось при тех же углах β , что и весовой эксперимент. Использовались внутримодельные дифференциальные датчики полного давления фирмы FREESCALE MPXV 5004D (максимальное давление 4 кПа), сигналы которых через аналогово-цифровой преобразователь фирмы National Instruments NI USB-6009 передавались на компьютерную обработку с выдачей данных в темпе эксперимента.

• 4.    Результаты испытаний

Результаты измерений аэродинамических коэффициентов сопротивления C _x , боковой силы C _y и крутящего момента m _z для здания в зависимости от угла β приведены на рис. 8–10. На рис. 11 приведен фактор неустойчивости галопирования Ден-Гартога D = C x + C .

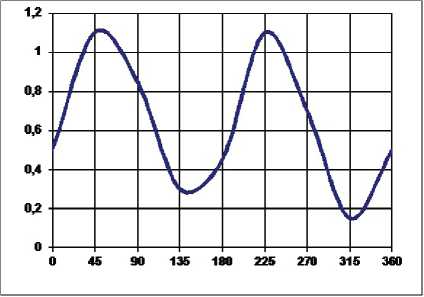
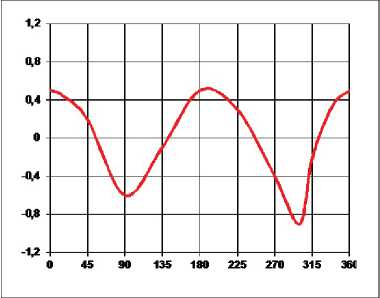
Рис. 8. Зависимость C x ( в )                         Рис. 9. Зависимость C _y ( в )

Анализ результатов экспериментов позволяет выявить следующие характерные особенности аэродинамического нагружения:

• —    обтекание здания по характеру качественно близко к крылу самолёта низкого аэродинамического качества с заостренными передней и задней кромками, в связи с чем наличие

большой боковой (нормальной направлению ветра) силы C y ~ 1 является естественным, так же как и очень большие величины локального разрежения ( C p ~ — 3 , 5) на небольших участках фасадных поверхностей и острых кромок;

• —    максимумы боковой силы по β приходятся на минимумы силы сопротивления C _x ,в результате чего максимальная результирующая аэродинамическая сила C r = ( C 2 + C 2 ) ¹ / ² не превосходит значения 1,15 . На это значение целесообразно ориентироваться при оценке нагрузок по требованиям СНиП;

• —    влияние здания застройки отчетливо видно из сравнения наветренного ( в ~ 90°) и подветренного ( в ~ 270°) направлений: здание заметно «затеняет» проявление боковой силы;

• —    фактор неустойчивости галопирования Ден-Гартога D = C x + C y для здания положителен во всей области изменения β , за исключением сектора углов ветра β около 45° и 270°, где величина D ~ 1. Это означает, что в указанном диапазоне углов ветра существуют необходимые (но недостаточные) условия аэродинамической неустойчивости галопирования. Анализ этой ситуации с использованием специального динамического колебательного стенда не входил в поставленную задачу в связи с тем, что удлинение здания менее 7 [1].

  

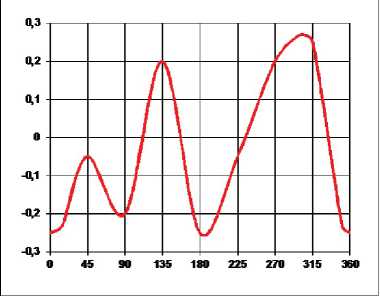
  Рис. 10. Зависимость m z ( в )

  
  
  

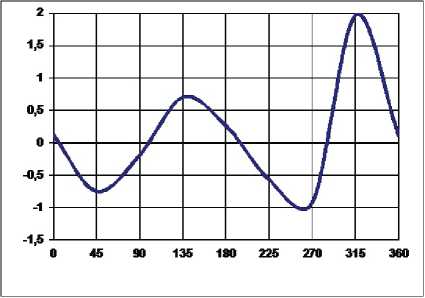
  Рис. 11. Зависимость D ( в )

  
  

При обработке сигнала мгновенного давления p ( t ) получены коэффициенты статического давления P , c p = ( p — p ^ ) /q ; среднеквадратичные пульсации давления pl ² = ( p — p ) ² ; пиковые значения реализации p _max и p _mi_n . Среди общих закономерностей распределенного нагружения следует отметить:

• —    наличие зон торможения потока на нормальных потоку участках поверхности зданий с характерными величинами коэффициента давления C p ~ 1;

• —    наличие обширных застойных зон с характерными C p ~ — 0 , 5;

• —    наличие небольших (3–5% длин сторон сечения) локальных зон ускоренного течения около острых углов здания с характерными значениями C p ~ — 3 , 5;

• —    практическую неизменность коэффициента среднего давления C p по высоте здания;

• —    умеренную интенсификацию пульсационной картины течения по высоте здания от нулевого уровня до крыши;

• —    практическое отсутствие влияния ПВС на характеристики давления на рассмотренных высотах h = 55 ми h = 90 м, обнаруженное при сравнительных испытаниях с ПВС и в равномерном потоке. На уровне, соответствующем натурной высоте 25 м, отличия достигают 15% в меньшую сторону в присутствии ПВС.

• 5.    Заключение

Сложная архитектурная форма здания приводит к зрительно сложной и далекой от практической необходимости информации по распределению давления для значений углов ветра из всего кругового диапазона от 0° до 360°. Эпюры давления показывают, что при рассмотрении массива данных для множества углов ветра в круговом диапазоне в каждой точке поверхности с очевидностью можно обнаружить с высокой вероятностью любое значение C p от C p max до C p min .

Поскольку в эксперименте непосредственно получены значения интегральных нагрузок, необходимость в использовании для их оценки процедуры интегрирования по поверхности зданий распределений давления отсутствует. Таким образом, использование характеристик распределений давления представляется необходимым только для анализа локального нагружения элементов фасадных систем.

В связи с однородностью структуры фасадных систем на поверхности здания и отсутствием нормативных требований по оценке нагрузок на отдельных выделенных элементах фасадной системы задача по локализации экстремальных локальных нагрузок не рассматривалась.

В качестве практических показателей для проектирования фасадных систем могут быть назначены предельные – максимальные и минимальные – значения указанных характеристик распределения давления по множеству всех внешних параметров испытаний – углам и точкам на поверхности зданий, которые приведены в табл. 2.

Таблица2 Сравнение интегральных характеристик

	C p max	C p min	VP' max /q	p max   p ro q	p min   p ro q
Основные участки поверхности здания	1,0	–0,6	0,09	1,15	–0,85
Области острых углов	—	–3,5	0,22	—	–0,7

• 1)    Аэродинамические коэффициенты сил и моментов, характеристики среднего и пульсационного давления, полученные в работе, соответствуют натурным и могут быть использованы при проектных расчетах зданий на ветровые нагрузки.

• 2)    При учёте ветрового нагружения по СНиП 2.01.07-85 нормативные значения средней составляющей ветровой нагрузки по высоте здания в терминах СНиП 2.01.07-85 определяются по формуле главы 6 с использованием аэродинамического коэффициента C (максимальное значение Cr для исследуемого объекта) для здания с =1 , 15. Т.е. нормативное значение средней составляющей интегральной ветровой нагрузки wm определяется как w m = 1,15 w 0 k , где w 0 – нормативное значение ветрового давления; k – коэффициент, берущийся из таблицы 6.2 СНиП 2.01.07-85.

• 3)    Уровень средних нагрузок разрежения в небольших областях, примыкающих к острым углам здания, существенно превосходит средний уровень на остальной поверхности, что целесообразно учесть при расчете элементов фасадной системы в непосредственной близости от углов зданий.